The consensus protocol Stellar was first described in a scientific article by David Mazier in 2015. It is a “federal Byzantine agreement system” that allows decentralized computing networks without leaders to effectively reach consensus on any decision. The Stellar payment network uses the Stellar Consensus Protocol (SCP) to maintain a consistent transaction history that all participants see.

Consensus protocols are considered difficult to understand. SCP is simpler than most of them, but still shares this reputation — partly because of the erroneous idea that the “federal vote” to which the first half of a research article is dedicated is SCP. But it is not so! This is only an important building block, which in the second half of the article is used to create the actual Stellar consensus protocol.

In this article we will briefly describe what the “system of agreements” is, what can make it “Byzantine”, and why make the Byzantine system “federal”. Then we will explain the federal voting procedure described in the SCP article, and, finally, we will explain the SCP protocol itself.
')

Agreement Systems

The system of agreements allows a group of participants to come to a consensus on some topic, for example, what to order for lunch.

At Interstellar, we have implemented our own dining agreement system: ordering what our operations manager, John, says. This is a simple and effective system of agreements. We all trust John and believe that every day he will find something interesting and nutritious.

But what if John misuses our trust? He can single-handedly decide that we all have to become vegans. In a week or two, we will probably overthrow him and transfer the powers to Elizabeth. But suddenly she loves avocados with anchovies and thinks that everyone should become like that. Power corrupts. Therefore, it is better to find some more democratic method: some way to make sure that different preferences are taken into account, while providing a timely and unambiguous result so that it does not happen that no one orders lunch or five people place different orders, or the discussion drags on until evening.

It would seem that the solution is simple: take a vote! But this is a deceptive impression. Who will collect the newsletters and report the results? And why should the rest believe what he says? Perhaps we can first vote for a leader whom we trust to lead the vote - but who will lead this first vote? What if we can't agree on a leader? Or if we agree, does this leader get stuck in a meeting or go to the hospital?

Similar problems are found in distributed computer networks. All participants or nodes must agree on a solution, for example, whose turn it is to update a common file or to take a task from the processing queue. In a cryptocurrency network, nodes repeatedly have to choose what the full story looks like from several possible versions that sometimes conflict. This network agreement gives a guarantee to the recipient that the coin is (a) valid (not fake) and (b) not yet spent elsewhere. It also guarantees that he will be able to spend coins in the future, because the new recipient will have the same guarantees for the same reasons.

Any matching system in a distributed computer network must be fault tolerant: it must produce consistent results, despite errors such as slow links, unresponsive nodes, and the wrong message order. The Byzantine system of agreements is additionally resistant to “Byzantine” errors: nodes that give false information, either because of an error or in a deliberate attempt to undermine the system or gain some advantage. “Byzantine” resiliency — the ability to trust a group decision, even when some members of the group may lie or otherwise not follow the rules of decision making — was named after the parable of the generals of the Byzantine Empire who tried to coordinate the attack. Anthony Stevens has a good description .

Consider the owner of a cryptomonet, Alice, who must choose between buying delicious ice cream from Bob and paying Carol debt. Perhaps Alice wants to pay both at once, fraudulently spending the same coin. To do this, she must convince Bob’s computer that the coin was never paid to Carol, and convince Carol’s computer that the coin was never paid to Bob. The Byzantine system of agreements makes it virtually impossible using the form of a majority rule, called a quorum . A node in such a network refuses to switch to a certain version of the story until it sees that a sufficient number of peer nodes - a quorum - agree to such a switch. Once this happens, they will form a sufficiently large electoral bloc to force the remaining network nodes to agree with their decision. Alice can make some nodes lie on her behalf, but if the network is big enough, then her attempt will be suppressed by the voices of honest nodes.

How many nodes are required for a quorum? At a minimum, the majority, or more precisely, the qualified majority to deal with errors and fraud. But in order to calculate the majority, you need to know the total number of participants. In the Interstellar office or district elections, these numbers are easy to recognize. But if your group is a weakly defined network, into which nodes can enter and exit at will without agreement with the center, then a federal Byzantine agreement system is needed that can determine quorums not from a predetermined list of nodes, but dynamically, from constantly changing and inevitably incomplete snapshot of nodes at a specific point in time.

It may seem impossible to create a quorum from the point of view of a single node on a vast network, but it is possible. Such a quorum can even guarantee the results of a decentralized vote. The SCP white paper shows how to do this using a procedure called federal voting .

For impatient

The rest of the article describes in more detail the federal vote and the Stellar consensus protocol. If you are not interested in the details, here is a general overview of the process.

1. Nodes conduct rounds of federal voting on "nominees". A round of federal voting means:
   
   • A node votes for a statement, for example, “I propose a V value”;
     
   • A node listens to the voices of peers until it finds one that can “accept”;
     
   • The site is looking for a “quorum” for this statement. The quorum "confirms" the nominee.
2. As soon as a node can confirm one or more nominees, it tries to “prepare” a “bulletin” through several rounds of federal voting.
   
3. As soon as the node is able to verify the readiness of the ballot, it tries to commit it using even more rounds of federal voting.
   
4. Once the node can confirm the commit of the newsletter, it can “externalize” the value of this newsletter, using it as a result of consensus.

These steps include several rounds of federated voting, which together form a single SCP round. We will understand in more detail what happens at each step.

Federated vote

Federated voting is the procedure for determining whether a network can agree on a proposal. In a voting round, each node must choose one of potentially many possible values. He cannot do this until he is sure that other nodes in the network will not choose a different result. To be sure of this, nodes exchange a flurry of messages back and forth, so that everyone confirms that the quorum of nodes makes the same decision . The rest of this section explains the terms in this sentence and how the whole procedure happens.

Quorums and Quorum Slices

Let's start by defining the quorum. As we discussed above, in a decentralized network with dynamic membership it is impossible to know in advance the number of nodes and, therefore, how much is needed for most. Federated voting solves this problem by introducing a new quorum slice idea: a small set of peers that the node trusts to transmit information about the state of the vote in the rest of the network. Each node determines its own quorum slice (of which it becomes a member after the fact).

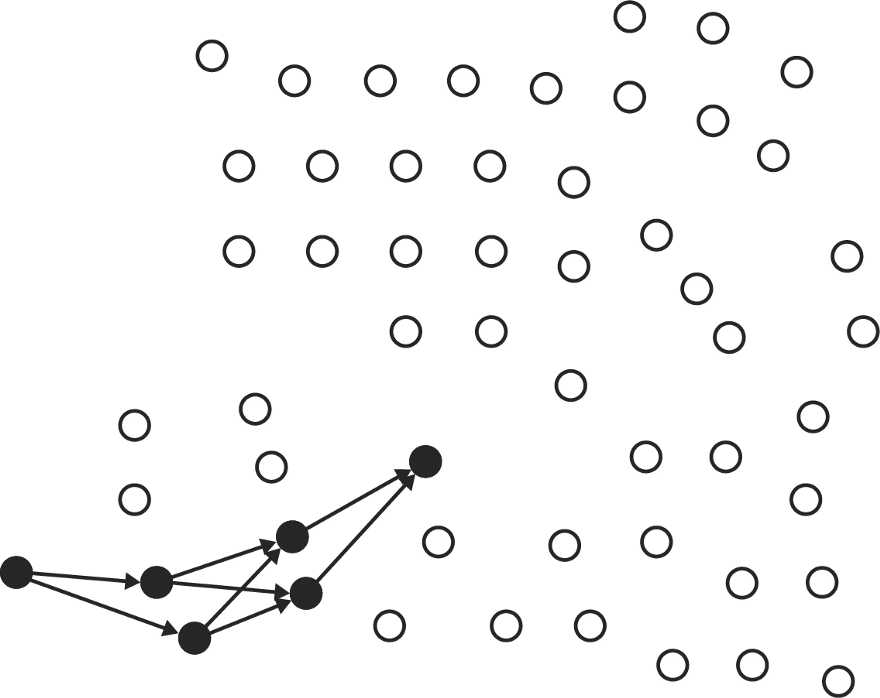
The formation of a quorum begins with a cut of the quorum. For each node, the nodes of its slice are added. Then the members of the slices of these nodes are added , and so on. As you continue, more and more nodes appear that you cannot add because they are already included in the slice. When there are no more new nodes to add, the process stops: we have formed a quorum by “transitive closure” (transitive closure) of the cut-off quorum of the initial node.


To find the quorum from this node ...


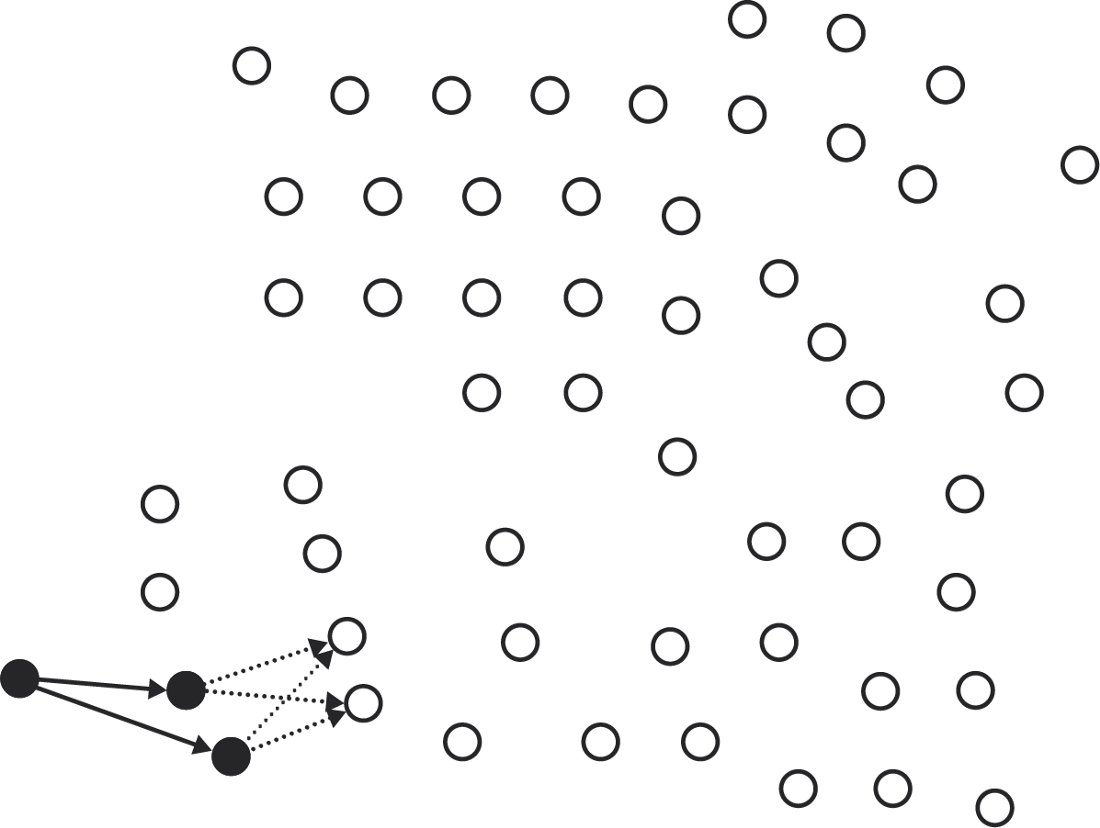
... we add members of its cutoff ...


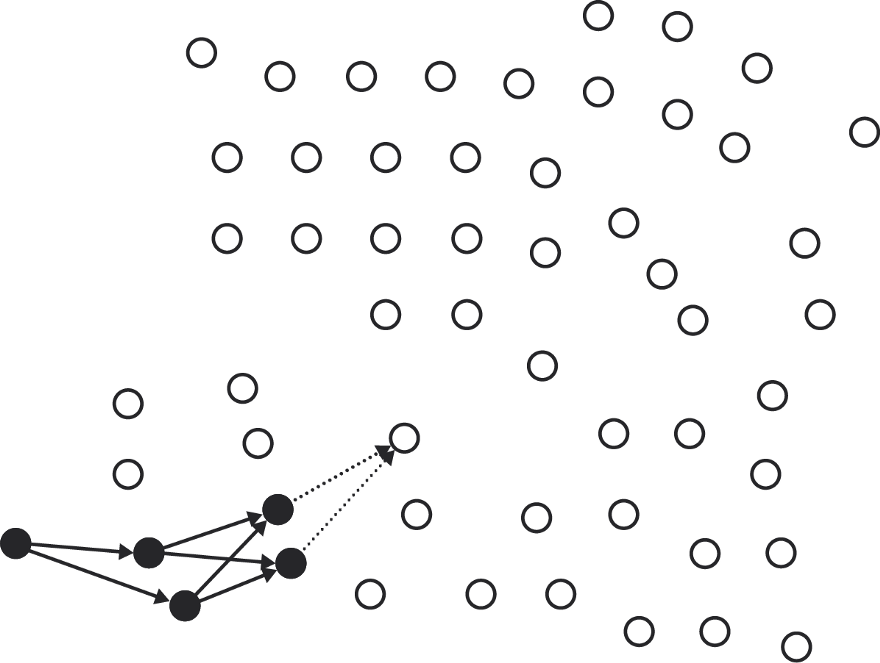
... then add members to the slices of these nodes.


We continue until there are nodes to add.




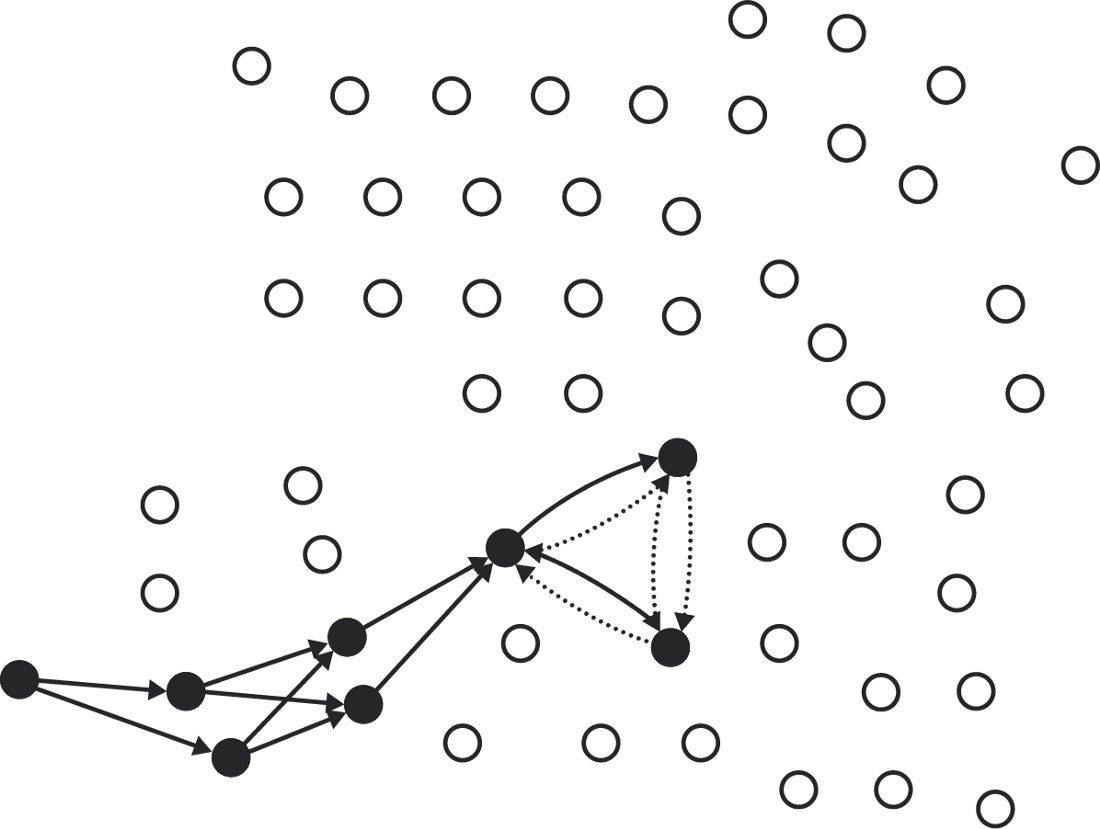
No nodes to add left. This is a quorum.

In fact, each node can go into more than one slice. To form a quorum, select only one of the slices and add members; then select any slice for each member and add members to that slice, and so on. This means that each node is a member of a set of possible quorums.


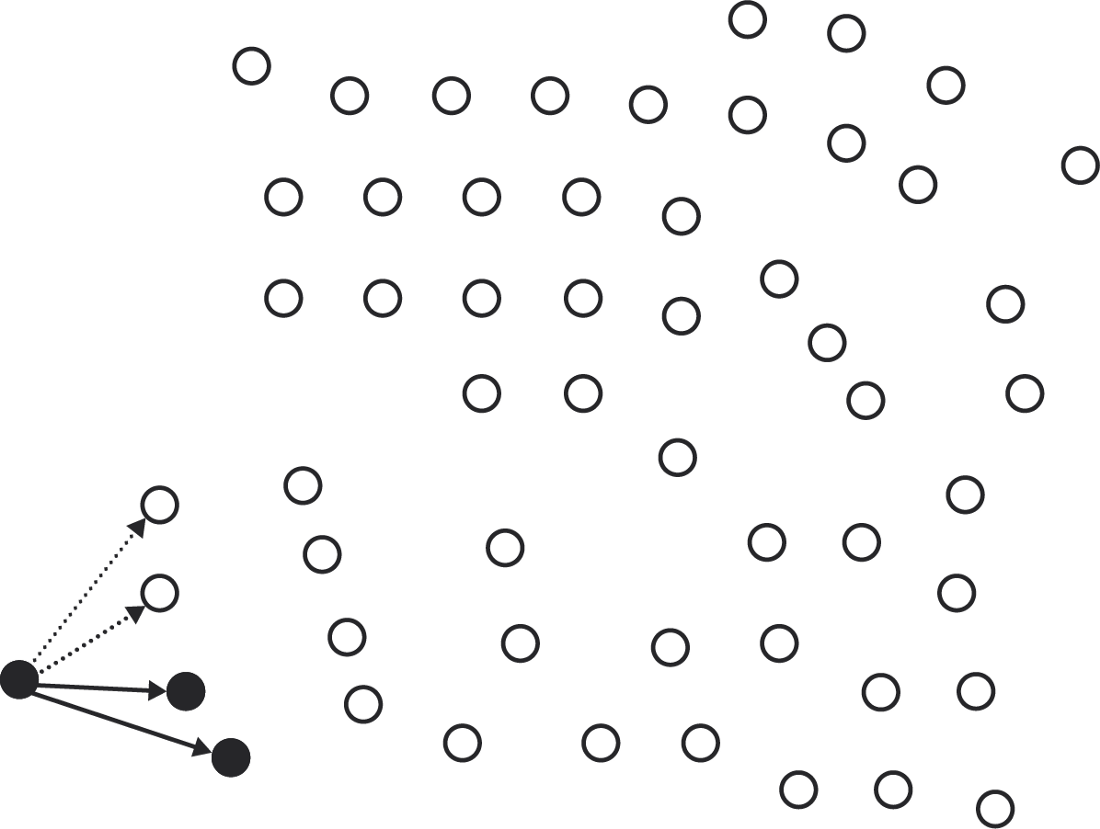
Select only one quorum slice at each step.






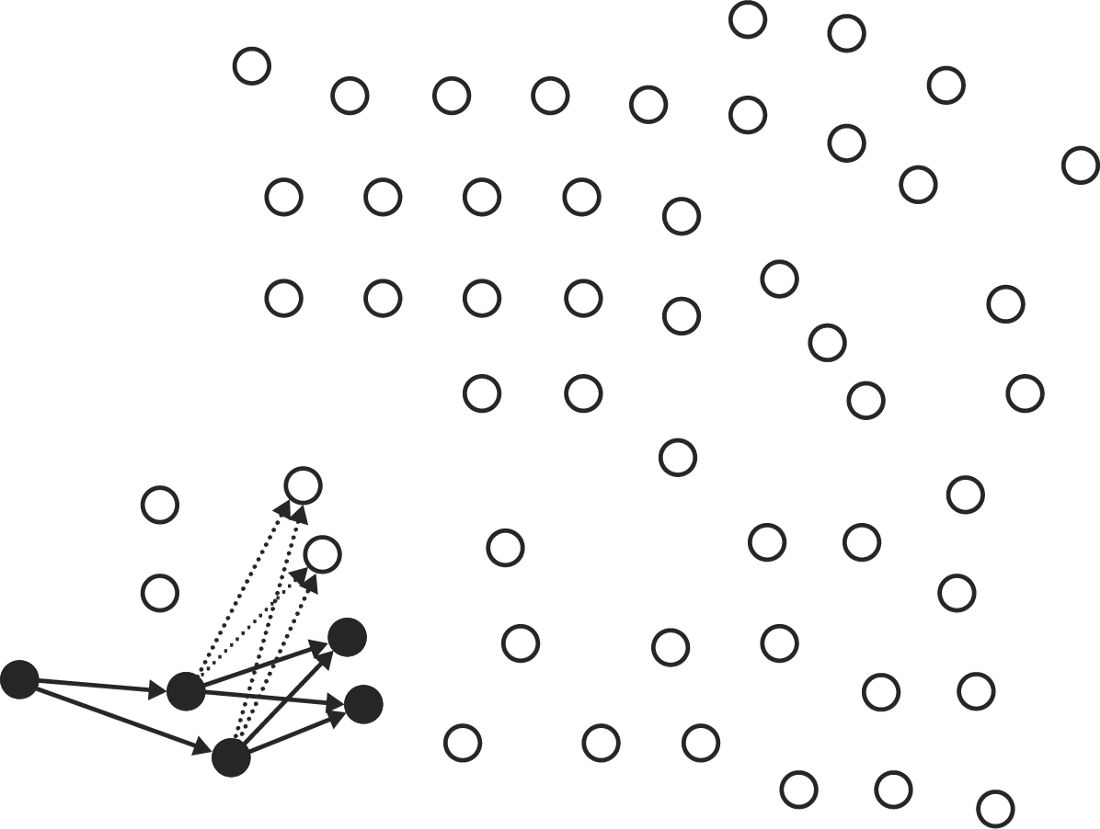
One possible quorum. Or an alternative ...


... choose other sections ...




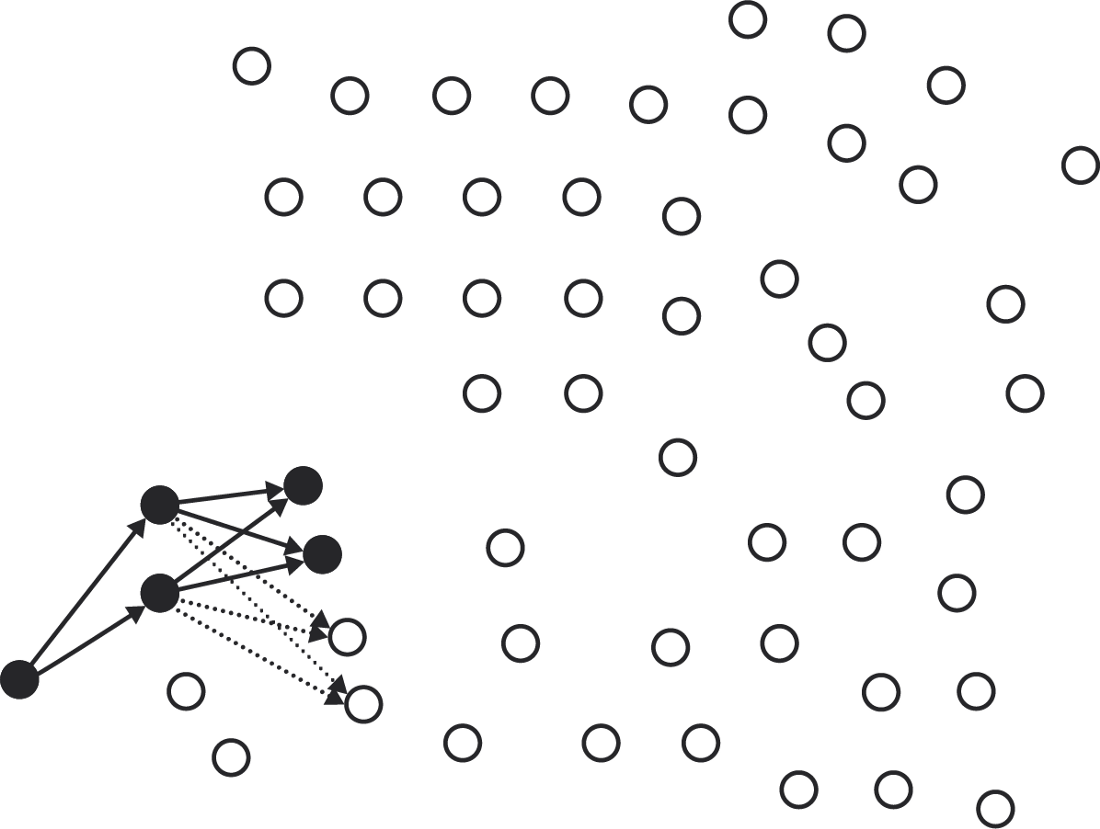
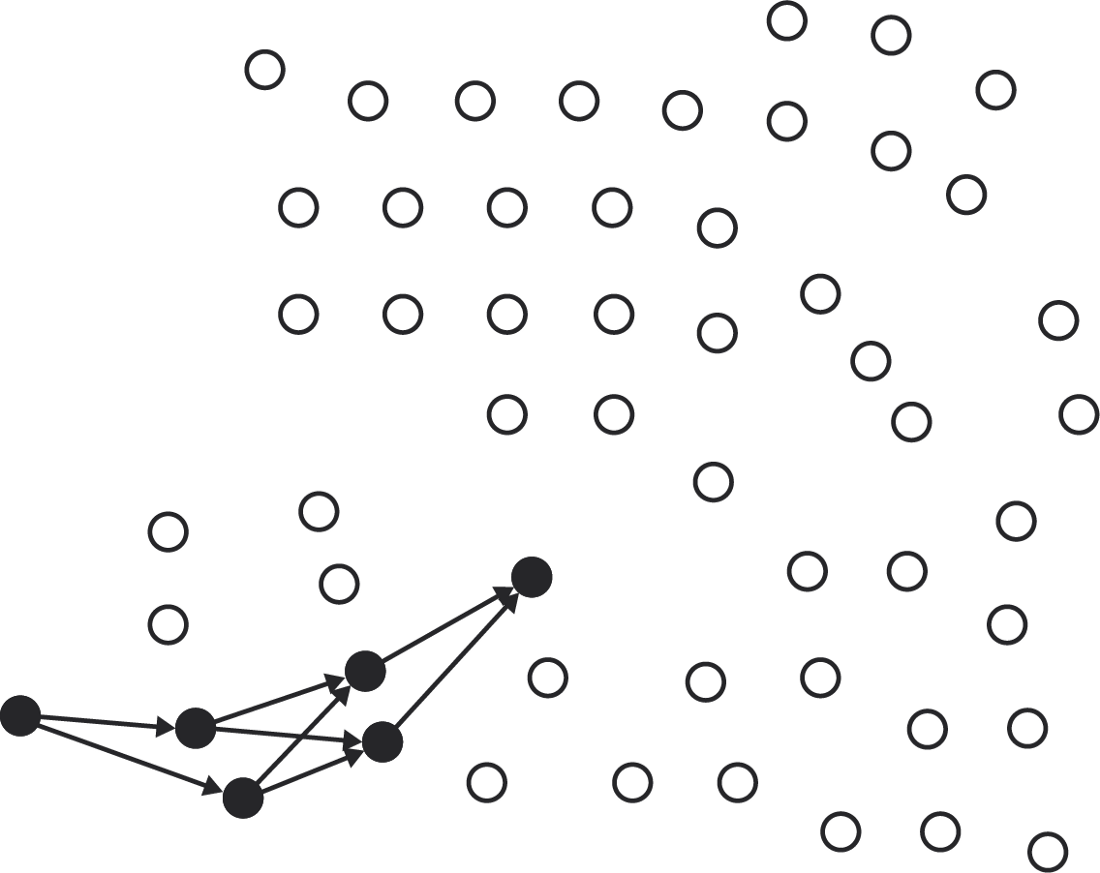
...(when it's possible)…


... creates another quorum.

How does the node know which slices the other nodes are in? In the same way as other information about other nodes: from the transmissions that each node broadcasts to the network when its voting status changes. Each broadcast includes information about the slicing of the sending node. The SCP technical document does not specify a communication mechanism. Implementations typically use the gossip protocol to ensure message translation across the entire network.

Recall that in a non-federal Byzantine system of agreements, a quorum is defined as the majority of all nodes. The Byzantine system of agreements is designed from the point of view of the question: how many dishonest nodes can the system carry? In a system of N nodes designed for survival with f failures (deceptions), the node must be able to make progress after receiving a response from N – f peers, since f of them may not function. But having received a response from N − f peers, it can be assumed that all f peers (from which the node received no response) are in fact honest. Thus, fs from N − f peers (from which the answer is received) are malicious. In order for the nodes to arrive at one consensus, most of the remaining nodes must be honest, that is, we need N − f to be greater than 2f or N> 3f. So usually, a system designed for survival with f failures will have a total of N = 3f + 1 nodes and a quorum size of 2f + 1. As soon as the proposal passes the quorum threshold, the rest of the network is convinced that any competing offers will fail. So the network converges to the result.

But in the federal Byzantine system of agreements, not only cannot there be a majority (because no one knows the overall size of the network), but the concept of the majority is generally useless! If the membership in the system is open, then someone can get the majority, simply by conducting the so-called attack of the Sibyl: repeatedly joining the network through several nodes. So why the transitive closure of the slice can be called a quorum , and how is it able to suppress competing offers?

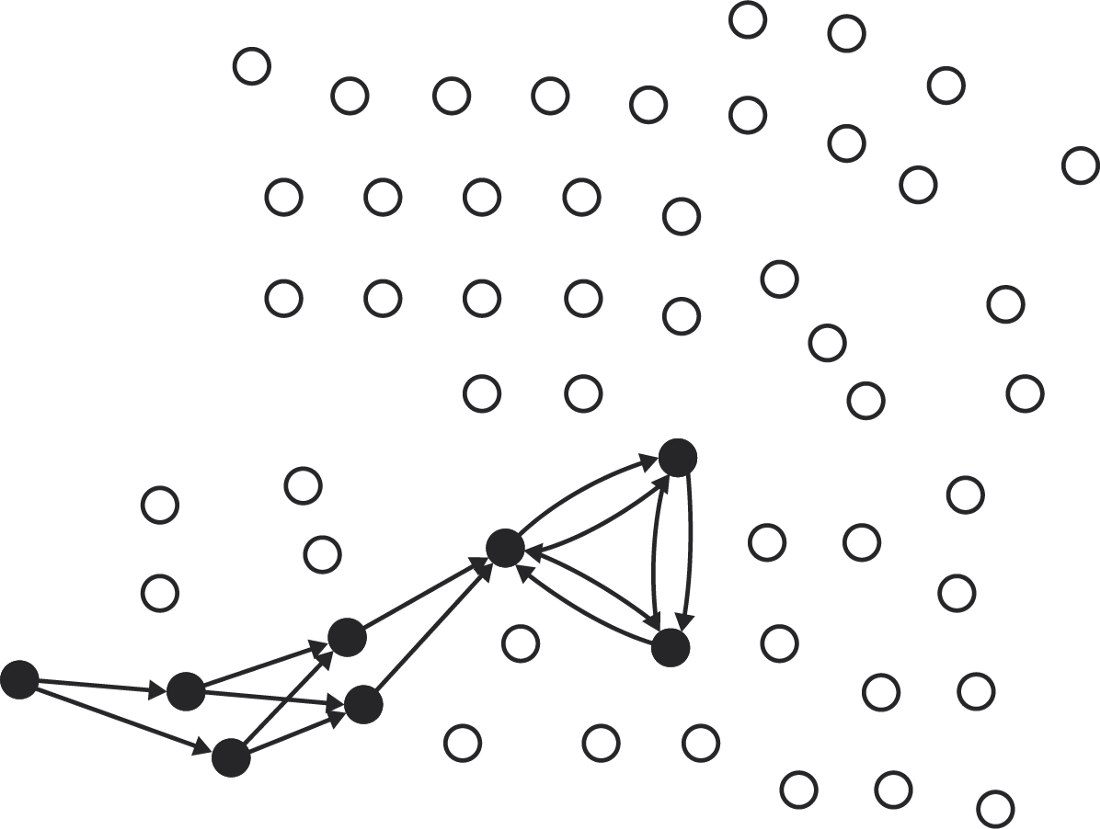
Technically, no way! Imagine a network of six nodes where two triples are isolated in each other's quorum slices. The first subgroup can make a decision about which the second will never hear, and vice versa. There is no way for this network to reach consensus (except by chance).

Therefore, the SCP requires that for federated voting (and for the application of the important theorems of the article) the network must have a property called quorum intersection . In a network with this property, any two quorums that can be built always overlap in at least one node. To determine the prevailing mood of the network is as good as having the majority. Intuitively, this means that if a quorum agrees with statement X, no other quorum can ever agree with something else, because it will necessarily include some node from the first quorum that has already voted for X.


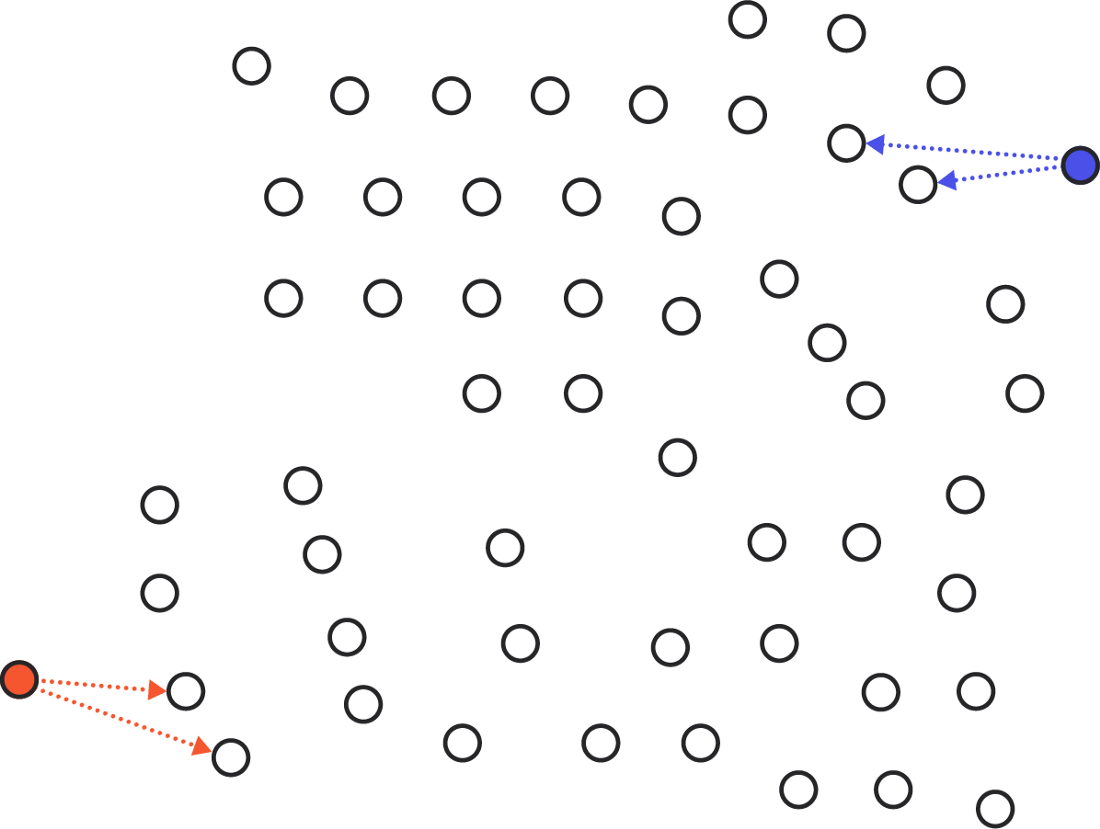
If the network has an intersection of quorums ...


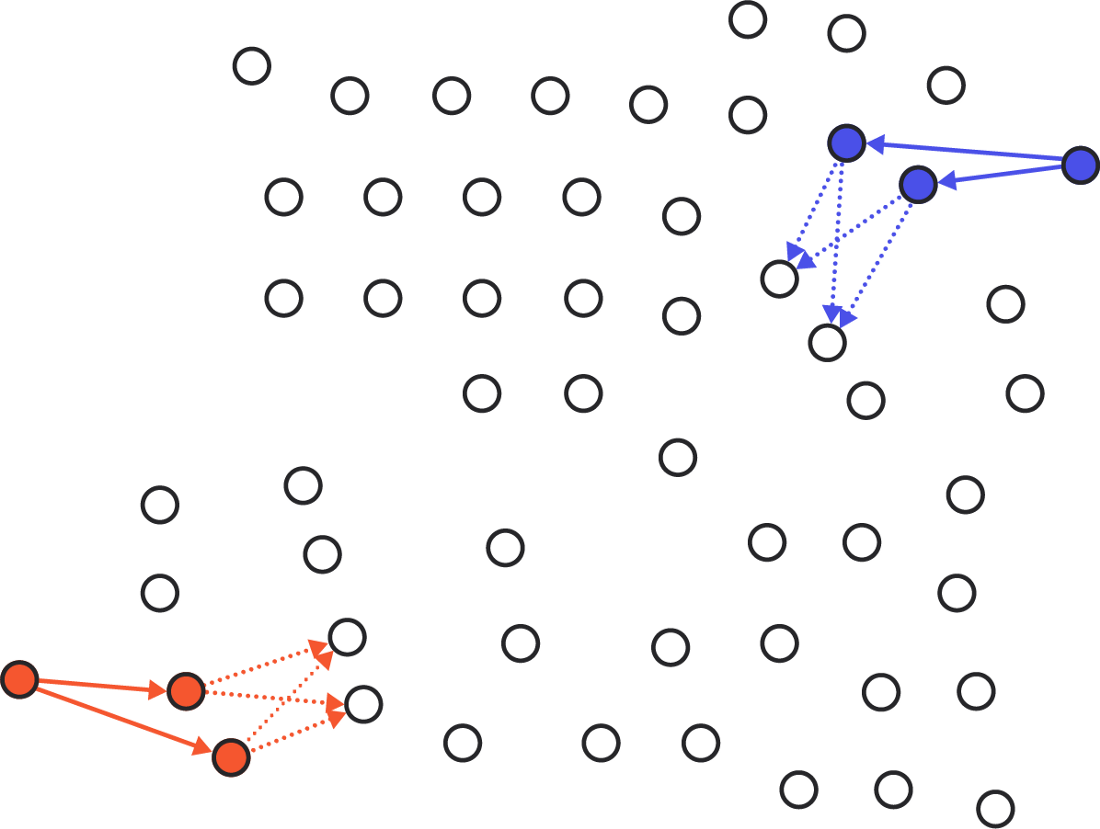
... then any two quorum you can build ...


... will always intersect.





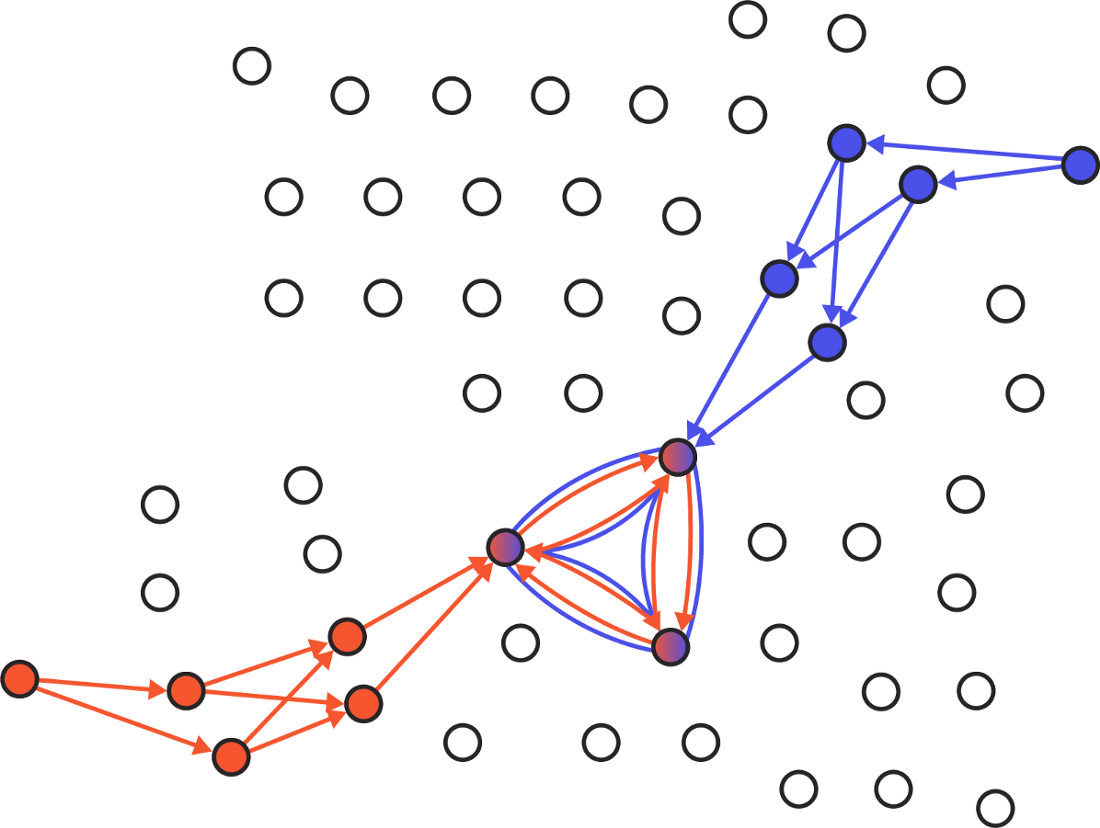
(Of course, overlapping nodes can be Byzantine false or bad in other ways. In this case, the intersection of quorums does not help the network to agree at all. For this reason, many of the results in the SCP technical document are based on explicit assumptions, such as what remains in the network intersection of quorums even after the removal of bad nodes . For simplicity, we leave these assumptions implicit in the rest of the article).

It may seem unreasonable to expect that in a network of independent nodes it is possible to reliably intersect quorums. But there are two reasons why this is so.

The first reason is the existence of the Internet itself. The Internet is an ideal example of a network of independent nodes with quorum intersection. Most of the nodes on the Internet connect to only a few other local nodes, but these small sets overlap enough for each node to be accessible from every other node along a particular route.

The second reason is specific to the Stellar payment network (the most common use of SCP). Each asset in the Stellar network has an issuer, and Stellar recommendations require that each issuer designate one or more nodes in the network to process redemption requests. It is in your interest to directly or indirectly include these nodes in quorum sections for each asset of interest. Then the quorums for all nodes interested in this asset will overlap at least in these nodes of maturity. The nodes interested in several assets will include all the redemption nodes of the respective issuers in their quorum sections, and they will strive to consolidate all the assets together. In addition, any assets that are not connected in this way with others on the network, and should not be linked - so conceived that for this network there is no crossing of quorums (for example, banks from the dollar zone sometimes want to trade with banks from the euro zone and banks from the peso zone, so they are on the same network, but none of them care about a separate network of children selling baseball cards).

Of course, waiting for quorum crossing is not a guarantee . Other Byzantine agreement systems owe their complexity to the guarantee of quorums. An important innovation of SCP is that it removes the responsibility for creating quorums from the consensus algorithm itself and brings it to the application level. Thus, although federal voting is fairly general for voting on any issues, in fact, its reliability critically depends on the wider meaning of these values. Some hypothetical uses may not be as convenient for creating well-connected networks as others.

Voting, acceptance and confirmation

In the round of federal voting, the node optionally begins to vote for some value V. This means broadcasting a message to the network: “I am node N, my slices of quorums Q, and I vote for V.” When a node votes in this way, it promises that it never voted against V and never will.

In peer-to-peer broadcasts, each node sees how the others vote. As soon as the node collects a sufficient number of such messages, it can track the quorum slices and try to find quorums. If he sees a quorum of peers who also vote for V, he can proceed to adopt V and broadcast this new message to the network: "I am node N, my sections of quorum Q, and I accept V". Adoption provides a stronger guarantee than simple voting. When a node votes for V, it can never vote for other options. But if a node accepts V, no other node on the Web will ever accept another option (Theorem 8 in the SCP technical paper proves this).

Of course, there is a high probability that there will not immediately be a quorum of nodes that will agree with V. Other nodes can vote for other values. But for a node there is another way to move from simple voting to adoption. N can take a different value of W, even if it did not vote for it, and even if it does not see a quorum for it. To decide to change your voice, it is enough to see the blocking set of nodes that have accepted W. The blocking set is one node of each of the slices of quorums N. As the name implies, it is able to block any other value. If all nodes in such a set accept W, then (by Theorem 8) it will never be possible to form a quorum that takes a different value, and therefore it is also safe for N to accept W.


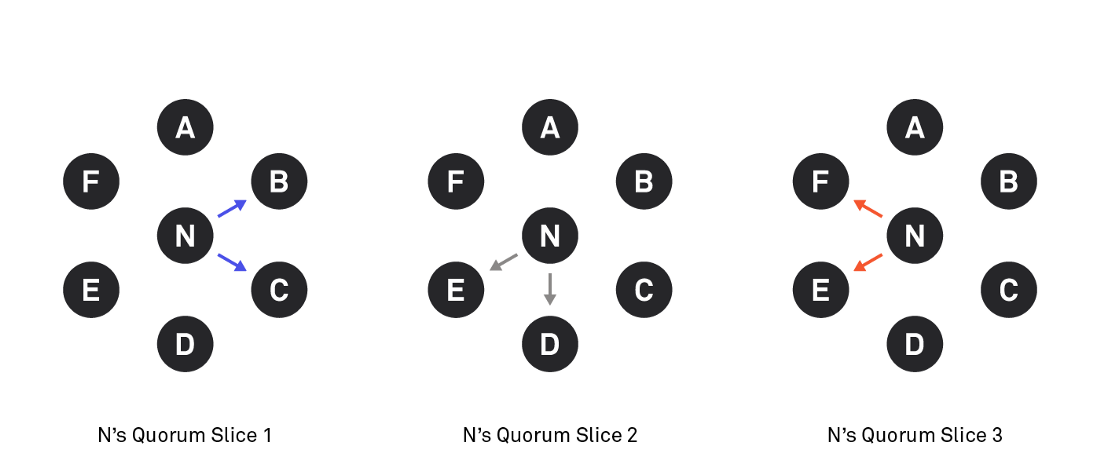
Node N with three slices of quorums.


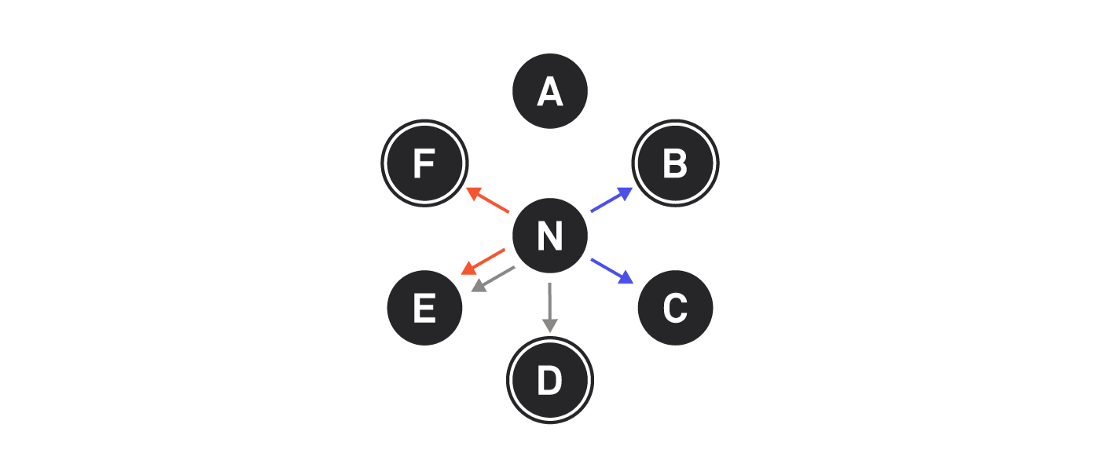
BDF is the blocking set for N: it includes one node of each of the slices N.


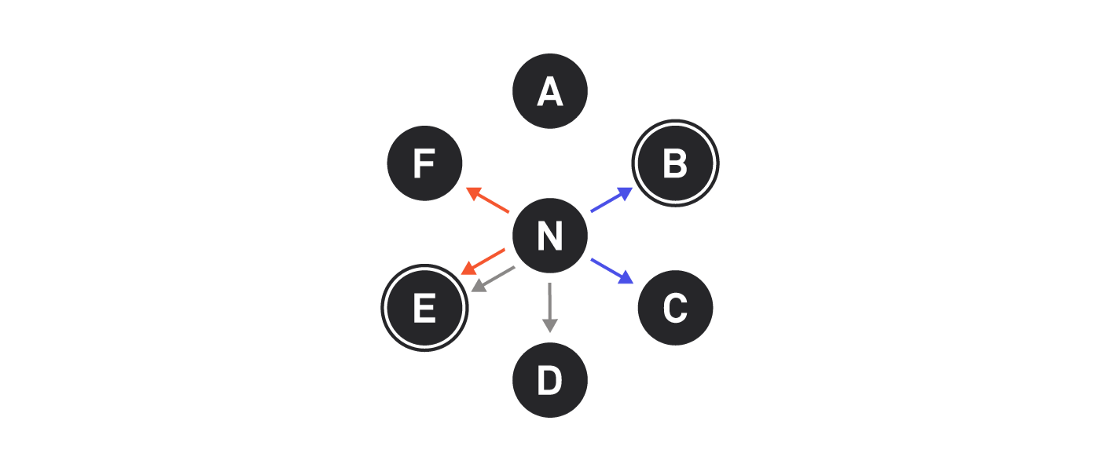
BE is also a blocking set for N, because E appears in two slices N.

But the blocking set is not a quorum. It would be too easy to deceive node N to assume the desired value if it is enough to crack just one node in each of the slices N. Therefore, accepting the value is not the end of the vote. Instead, N must confirm the value, that is, see the quorum of the nodes receiving it. If he goes this far, then, as the SCP technical document proves (in Theorem 11), the rest of the network will also ultimately confirm the same value, so N will complete the federative vote with a certain value as a result.


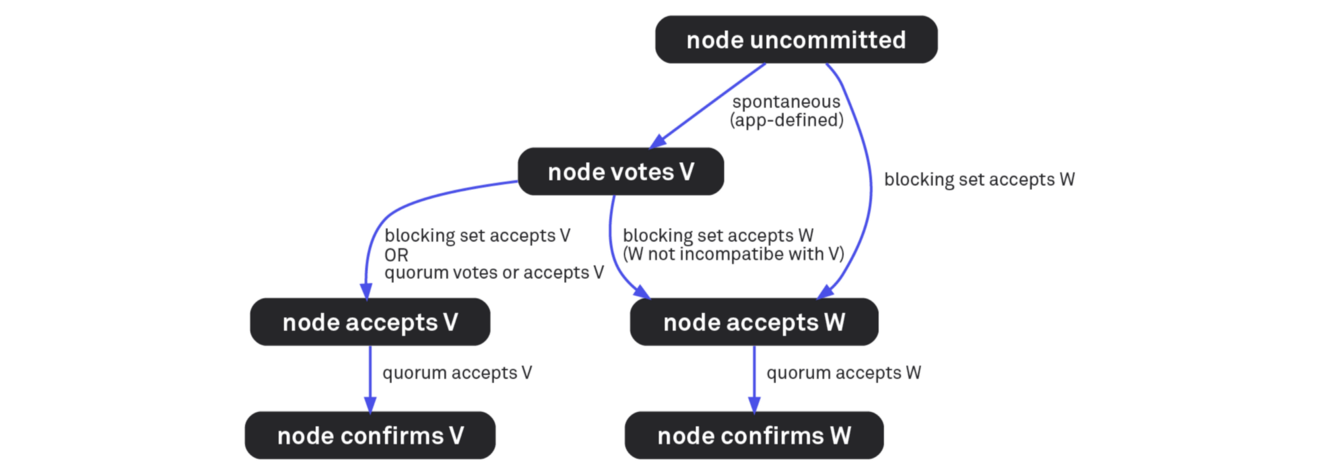
Federated voting.

The voting, acceptance and confirmation process constitutes one full round of federal voting. The Stellar Consensus Protocol combines many such rounds to create a complete consensus system.

Consensus protocol Stellar

The two most important properties of the consensus system are security and survivability . A consensus algorithm is “safe” if it can never give different results to different participants (a copy of Bob’s story will never contradict Carol). “Vitality” means that the algorithm will always produce a result, that is, it will not get stuck.

The federated voting procedure described is safe in the sense that if a node confirms the value of V, no other node will confirm another value. But "will not confirm another meaning" - this does not mean that he will confirm something. Participants can vote for such a large number of different values ​​that nothing reaches the acceptance threshold. This means that there is no survivability in federative voting.

The consensus protocol Stellar uses federated voting in such a way as to guarantee both security and survivability. (The security guarantees and survivability of the SCP have a theoretical limit. The design chooses a very strong guarantee of safety, sacrificing a slight weakening of survivability, but given sufficient time, consensus is very likely to be reached). In a nutshell, the idea is to run several federated polls on several values, until one of them passes completely through all the SCP voting phases described below.

The values ​​by which the SCP seeks consensus may be a transaction history or a lunch order, or something else, but it is important to note that these are not values ​​that are accepted or confirmed. Instead, a federal vote occurs on claims about these values .

The first rounds of federative voting take place at the nomination phase, on a set of “I nominate V” statements, possibly for many different values ​​of V. The goal of the nomination is to find one or more statements that go through acceptance and confirmation.

After finding the confirmed candidates, the SCP proceeds to the voting stage, where the goal is to find some bulletin (that is, a container for the proposed value) and a quorum that can declare a commit for it (commit). If a quorum commits a ballot, its value is accepted as a consensus. But before the node can vote for a commit ballot, it must first confirm the cancellation of all ballots with a lower counter value. These steps — the abolition of ballots to find one for which you can confirm a commit — include several rounds of federal voting on several bulletin statements.

The following sections describe promotion and voting in more detail.

Advancement

At the beginning of the nomination stage, each node can spontaneously choose the value of V and vote for the statement “I put forward V”. The goal at this stage is to confirm the nomination of a certain value by means of federal voting.

It is possible that a sufficient number of nodes vote for quite different statements, and no nomination can reach the acceptance threshold. Therefore, in addition to broadcasting their own nomination votes, the nodes “reflect” the nominations of their peers. Reflection (echo) means that if a node votes for nomination V, but sees a message from a neighbor voting for nomination W, it will now vote for nomination of both V and W. (Not all peer voices are reflected during the nomination, because this can lead to an explosion of different nominees.The SCP includes a mechanism for regulating these voices. In short, there is a formula for determining the “priority” of a peer from the point of view of a node, and only the votes of high-priority nodes are reflected. the set of peers whose voices it will reflect.The priority formula as one of the input data includes the slot number, therefore the high priority peer for one slot may be low priority for another, and vice versa).

Conceptually, the nomination of both V and W in parallel is separate federal voices, each individually capable of attaining acceptance or confirmation. In practice, SCP messages pack these individual voices together.

Although voting for nomination V is a promise never to vote against nomination V, at the application level — in this case SCP — it is defined what means “against”. The SCP does not see a statement that contradicts the “I nominate X” vote, that is, there is no “I am against X nomination” message, so the node can vote to nominate any values. Many of these nominations will lead nowhere, but ultimately the node will be able to accept or confirm one or more values. As soon as the nominee is confirmed, he becomes a candidate .


Nomination of SCP using federated voting. There may be many “B” values ​​pushed by peers and “mirrored” by a node.

Nomination of candidates may result in several confirmed candidates. Therefore, the SCP requires the application layer to provide some method of combining candidates into a single composite (composite). The merge method can be any. The main thing is that if this method is deterministic, then each node will combine the same candidates.In the voting system for the lunch "union" can simply mean the rejection of one of the two candidates. (But in a deterministic way: each node must choose the same value to reset. For example, an earlier selection in alphabetical order). In the Stellar payment network, where voting for transaction history takes place, combining the two proposed nominees involves combining the transactions they contain and the last of their two timestamps.

The technical description of the SCP proves (Theorem 12) that by the end of the extension phase, the network eventually converges to a single composite. But there is a problem: federated voting is an asynchronous protocol (like SCP). In other words, nodes are not coordinated by time, but only by messages that are sent. From a node's point of view, it is unclear when it ended.extension phase. And although all nodes will eventually come to the same composite, they can choose different routes along the way, creating different composite candidates on the way, and can never tell which one is final.

But it normal.Nomination - only preparation. The main thing to limit the number of candidates to reach a consensus, which occurs in the process of balloting (balloting).

Ballot

A bulletin is a pair of <counter, value>, where counter is an integer that starts with 1, and value is a candidate from the nomination stage. This can be a node’s own candidate or a neighbor’s candidate accepted by that node. Roughly speaking, when running for balloting, repeated attempts are being made to force the network to reach consensus on some candidate in a certain ballot by holding potentially many federal votes on statements about ballots. Bulletin counters track attempts made, and higher-counted ballots take precedence over lower-counted ballots. If the bulletin <counter, value> is stuck, a new vote begins, now on the bulletin <counter + 1, value>.

It is important to distinguish between values.(for example, what should be the order for lunch: pizza or salads), bulletins (counter-value pair) and statements about bulletins. The SCP round includes several rounds of federal voting, in particular, on such statements:

• “I am ready to commit to bulletin B” and
  
• “I announce the committ of bulletin B”

From the point of view of this node, consensus is reached when it finds bulletin B, for which it can confirm (that is, find the quorum accepting) the statement “I announce the committ of bulletin B”. From this point on, you can safely act on the value specified in B — for example, place this order for lunch. This is called externalization of meaning. Once the acceptance of the bulletin is confirmed, the node can be sure that any other node has externalized the same value or necessarily will make it future.

Although conceptually many federated ballots are held on statements of many different ballots, they do not exchange as many messages, because each message encapsulates a number of ballots. One message thus promotes the state of many federated polls at once, for example: “I accept a commit of ballots ranging from <min, V> to <max, V>”.

What does the term “prepared” (prepared) and “commit” mean?

A node votes for a newsletter commit when it is convinced that other nodes will not commit newsletters with different values. The conviction is the purpose of the preparation of the application. A vote that says: “I am ready to commit newsletter B” is a promise to never commit a newsletter less than B, i.e. with a smaller counter (the SCP requires that the values ​​in the ballots have a certain order. bulletin <N1, V1> is less than <N2, V2> if N1 <N2, and also if N1 = N2 and V1 <V2). These smaller ballots are “rejected” (aborted) during the preparatory voting, while B is considered “prepared”.

Why "I am ready to commit a bulletin B" means "I promise never to allow commits of ballots less than B"? Because SCP defines abort as the opposite of commit. Voting on the preparation of a ballot paper also implies voting on the cancellation of some other ballots, and, as we discussed earlier, voting for one thing is a promise to never vote against it.

Before broadcasting a commit, a node must first find a newsletter, which it can confirm as prepared. In other words, he conducts a federal vote on the topic “I am ready to commit newsletter B”, perhaps for many different ballots, until he finds one that accepts a quorum.

Where do the voting ballots come from? First, the node translates the preparation for voting for <1, ​​C>, where C is the composite candidate made at the nomination stage. However, even after the start of preparation for voting, the nomination may lead to the appearance of additional candidates who will become new ballots. Meanwhile, peers may have different candidates, and they can form a blocking set that accepts “I am ready for the commit of bulletin B2”, which will convince the node to accept it too. Finally, there is a timeout mechanism that generates new rounds of federated voting on new ballots with higher counters if current ballots are stuck.

As soon as the node finds the bulletin B, which can confirm as prepared, it transmits a new message “Commit of bulletin B”. This vote tells the feasts that the node will never give up on B. In fact, if B is a bulletin <N, C>, then “Commit <N, C>” means unconditional consent to vote for the readiness of each bulletin from <N, C> to <∞, c>. This additional value helps other nodes catch up with the commit peer if they are still at earlier stages of the protocol.

At this stage it is worth emphasizing once again that these are asynchronous protocols. Just because a single node sends votes for a commit does not mean that its peers do it too. Some of them can still vote on statements to prepare for the vote, others may have already externalized significance. The SCP explains how a node should process each type of peer message, regardless of its phase.

If the message “I declare a commit <N, C>” cannot be accepted or confirmed, then there is a probability of accepting or confirming the message <N + 1, > or <N + 2, > - or, in any case, any newsletter with a value of C, and not any other, since the node has already promised never to cancel <N, C>. By the time the node broadcasts voices for a commit, it will be C or nothing, depending on how far the consensus goes. However, this is not enough for the node to externalize C. Some Byzantine feasts (constituting less than a quorum, based on our assumptions about security) may lie to the node. Accepting and then confirming some kind of bulletin (or a range of bulletins) is what gives the node the confidence to finally externalize C.


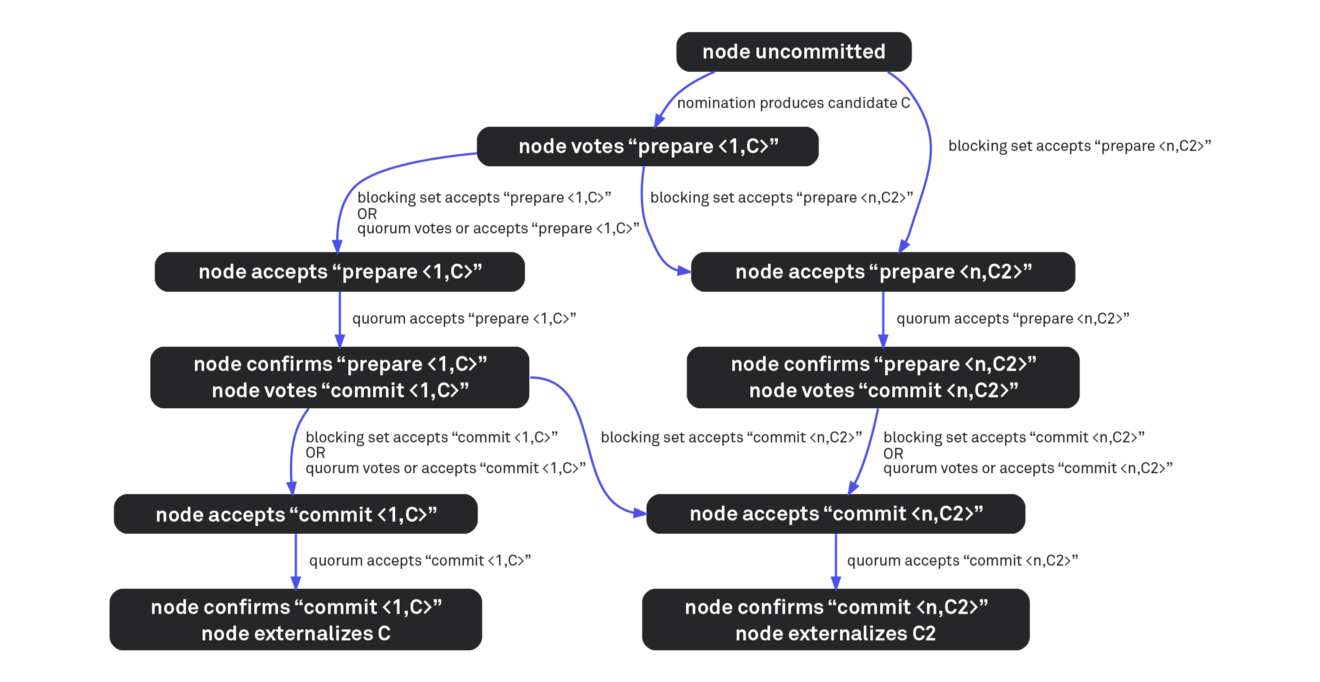
SCP balloting through federated vote. Not shown: at any time a timer may work by increasing the count in the bulletin (and, possibly, to produce a new composite of additional candidates nominated).

And it's all! Once the network has reached a consensus, it is ready to do it again and again. In the Stellar payment network, this happens about once every 5 seconds: a feat that requires both security and survivability, guaranteed by SCP.

The SCP can do this by relying on several rounds of federal voting. Federal voting was made possible thanks to the concept of quorum slices: sets of peers, which each node decided to trust as part of its (subjective) quorum. This configuration means that it is possible to come to a consensus even in a network with open membership and Byzantine deceptions.

• SCP , .
  
• SCP ( ) .
  
• , , «» « ». SCP , . .
  
• , SCP.
  
• For readers interested in SCP implementations: see the C ++ code used by the Stellar payment network, or the Go code , which I wrote for a better understanding of SCP.