Big o
Note. Abbreviated translation, rather retelling in your own words.
UPD: as noted in the comments, the examples are not perfect. The author is not looking for the best solution to the problem, his goal is to explain the complexity of the algorithms "on the fingers."
Big O notation is needed to describe the complexity of the algorithms. For this, the concept of time is used. The topic for many is frightening, programmers who avoid talking about “time of order N” are common.
If you are able to evaluate the code in terms of Big O, most likely you are considered a “smart guy.” And most likely you will pass your next interview. You will not be stopped by the question whether it is possible to reduce the complexity of any piece of code to n log n versus n ^ 2.
')
The choice of data structure depends on the specific task: on the type of data and the algorithm of their processing. Various data structures (in .NET or Java or Elixir) were created for certain types of algorithms.
Often, choosing this or that structure, we simply copy the generally accepted solution. In most cases this is enough. But in fact, without understanding the complexity of the algorithms, we cannot make an informed choice. The topic of data structures can only be taken after the complexity of the algorithms.
Here we will use only arrays of numbers (just like at the interview). JavaScript examples.
Take an array of 5 numbers:
Suppose you need to get the first element. Use for this index:
How complex is the algorithm? We can say: “not at all difficult - just take the first element of the array”. This is true, but it is more correct to describe the complexity in terms of the number of operations performed to achieve the result, depending on the input (input operations ).
In other words: how much will the number of operations increase with an increase in the number of input parameters.
In our example, the input parameters are 5, because there are 5 elements in the array. To get the result, you need to perform one operation (take the element by index). How many operations are required if the array elements will be 100? Or 1000? Or 100,000? All the same, only one operation is needed.
Ie: “one operation for all possible input data” - O (1).
O (1) can be read as “complexity of order 1” (order 1), or “the algorithm is executed in constant / constant time” (constant time).
You have already guessed that O (1) algorithms are the most efficient.
Now let's find the sum of the elements of the array:
Again we ask ourselves: how many input operations will we need? Here you need to sort through all the elements, i.e. operation on each item. The larger the array, the more operations.
Using Big O notation: O (n), or "complexity of order n (order n)". Also, this type of algorithm is called "linear" or that the algorithm is "linearly scaled."
Can we make summation more efficient? In general, no. And if we know that the array is guaranteed to start with 1, is it sorted and does not have spaces? Then you can apply the formula S = n (n + 1) / 2 (where n is the last element of the array):
Such an algorithm is much more efficient than O (n), moreover, it is executed in “constant / constant time”, i.e. this is O (1).
In fact, the operations are not the only one: you need to get the length of the array, get the last element, perform multiplication and division. Isn't that O (3) or something like that? In Bio O notation, the actual number of steps is not important, it is important that the algorithm is executed in constant time.
Algorithms with constant time are always O (1). Also with linear algorithms, in fact, operations can be O (n + 5), in Big O notation it is O (n).
Let's write a function that checks the array for duplicates. Nested loop solution:
We already know that array iteration is O (n). We have a nested loop, for each element we iterate again - i.e. O (n ^ 2) or "complexity of order n square".
Algorithms with nested loops for the same collection are always O (n ^ 2).
In the example above, a nested loop, by itself (if you do not take into account that it is nested) has complexity O (n), since It is an enumeration of the array elements. This cycle ends as soon as the necessary element is found, i.e. in fact, all the elements will not necessarily be enumerated. But in the Big O notation, the worst option is always considered - the desired element may be the most recent.
Here, a nested loop is used to search for a given element in an array. The search for an element in an array, under certain conditions, can be optimized — done better than linear O (n).
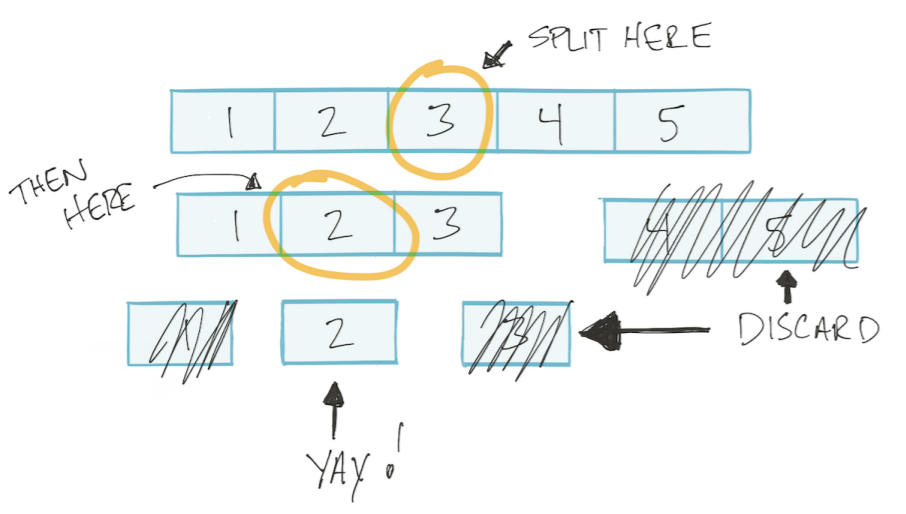
Let the array be sorted. Then we will be able to use the binary search algorithm: divide the array into two halves, discard the unnecessary, divide the rest again into two parts, and so until we find the desired value. This type of algorithm is called Divide and Conquer Divide and Conquer.
This algorithm is based on logarithm.
Consider an example of what will be x?
x ^ 3 = 8
We need to take the cubic root of 8 - it will be 2. Now it is more difficult
2 ^ x = 512
Using logarithm, the problem can be written as
log2 (512) = x
“The logarithm of base 2 from 512 is x”. Note the “base 2”, i.e. we think in twos - how many times you need to multiply 2 to get 512.
In the “binary search” algorithm, at each step we divide the array into two parts.
My addition. Those. at worst, we do as many operations as we can divide the array into two parts. For example, how many times can we divide into two parts an array of 4 elements? 2 times. And an array of 8 elements? 3 times. Those. number of divisions / operations = log2 (n) (where n is the number of array elements).
It turns out that the dependence of the number of operations on the number of input elements is described as log2 (n)
Thus, using the Big O notation, the “binary search” algorithm has O (log n) complexity.
Let's return to the task of checking the array for doubles. We went through all the elements of the array and for each element we did another search. Did O (n) inside O (n), i.e. O (n * n) or O (n ^ 2).
We can replace the nested loop with a binary search. Those. we still have to iterate over all elements of O (n), inside we do O (log n). It turns out O (n * log n), or O (n log n).
UPD: as noted in the comments, the examples are not perfect. The author is not looking for the best solution to the problem, his goal is to explain the complexity of the algorithms "on the fingers."
Big O notation is needed to describe the complexity of the algorithms. For this, the concept of time is used. The topic for many is frightening, programmers who avoid talking about “time of order N” are common.
If you are able to evaluate the code in terms of Big O, most likely you are considered a “smart guy.” And most likely you will pass your next interview. You will not be stopped by the question whether it is possible to reduce the complexity of any piece of code to n log n versus n ^ 2.
')
Data structures
The choice of data structure depends on the specific task: on the type of data and the algorithm of their processing. Various data structures (in .NET or Java or Elixir) were created for certain types of algorithms.
Often, choosing this or that structure, we simply copy the generally accepted solution. In most cases this is enough. But in fact, without understanding the complexity of the algorithms, we cannot make an informed choice. The topic of data structures can only be taken after the complexity of the algorithms.
Here we will use only arrays of numbers (just like at the interview). JavaScript examples.
Let's start with the simplest: O (1)
Take an array of 5 numbers:
const nums = [1,2,3,4,5]; Suppose you need to get the first element. Use for this index:
const nums = [1,2,3,4,5]; const firstNumber = nums[0]; How complex is the algorithm? We can say: “not at all difficult - just take the first element of the array”. This is true, but it is more correct to describe the complexity in terms of the number of operations performed to achieve the result, depending on the input (input operations ).
In other words: how much will the number of operations increase with an increase in the number of input parameters.
In our example, the input parameters are 5, because there are 5 elements in the array. To get the result, you need to perform one operation (take the element by index). How many operations are required if the array elements will be 100? Or 1000? Or 100,000? All the same, only one operation is needed.
Ie: “one operation for all possible input data” - O (1).
O (1) can be read as “complexity of order 1” (order 1), or “the algorithm is executed in constant / constant time” (constant time).
You have already guessed that O (1) algorithms are the most efficient.
Iterations and "time of order n": O (n)
Now let's find the sum of the elements of the array:
const nums = [1,2,3,4,5]; let sum = 0; for(let num of nums){ sum += num; } Again we ask ourselves: how many input operations will we need? Here you need to sort through all the elements, i.e. operation on each item. The larger the array, the more operations.
Using Big O notation: O (n), or "complexity of order n (order n)". Also, this type of algorithm is called "linear" or that the algorithm is "linearly scaled."
Analysis
Can we make summation more efficient? In general, no. And if we know that the array is guaranteed to start with 1, is it sorted and does not have spaces? Then you can apply the formula S = n (n + 1) / 2 (where n is the last element of the array):
const sumContiguousArray = function(ary){ //get the last item const lastItem = ary[ary.length - 1]; //Gauss's trick return lastItem * (listItem + 1) / 2; } const nums = [1,2,3,4,5]; const sumOfArray = sumContiguousArray(nums); Such an algorithm is much more efficient than O (n), moreover, it is executed in “constant / constant time”, i.e. this is O (1).
In fact, the operations are not the only one: you need to get the length of the array, get the last element, perform multiplication and division. Isn't that O (3) or something like that? In Bio O notation, the actual number of steps is not important, it is important that the algorithm is executed in constant time.
Algorithms with constant time are always O (1). Also with linear algorithms, in fact, operations can be O (n + 5), in Big O notation it is O (n).
Not the best solutions: O (n ^ 2)
Let's write a function that checks the array for duplicates. Nested loop solution:
const hasDuplicates = function (num) { //loop the list, our O(n) op for (let i = 0; i < nums.length; i++) { const thisNum = nums[i]; //loop the list again, the O(n^2) op for (let j = 0; j < nums.length; j++) { //make sure we're not checking same number if (j !== i) { const otherNum = nums[j]; //if there's an equal value, return if (otherNum === thisNum) return true; } } } //if we're here, no dups return false; } const nums = [1, 2, 3, 4, 5, 5]; hasDuplicates(nums);//true We already know that array iteration is O (n). We have a nested loop, for each element we iterate again - i.e. O (n ^ 2) or "complexity of order n square".
Algorithms with nested loops for the same collection are always O (n ^ 2).
"The complexity of the order of log n": O (log n)
In the example above, a nested loop, by itself (if you do not take into account that it is nested) has complexity O (n), since It is an enumeration of the array elements. This cycle ends as soon as the necessary element is found, i.e. in fact, all the elements will not necessarily be enumerated. But in the Big O notation, the worst option is always considered - the desired element may be the most recent.
Here, a nested loop is used to search for a given element in an array. The search for an element in an array, under certain conditions, can be optimized — done better than linear O (n).
Let the array be sorted. Then we will be able to use the binary search algorithm: divide the array into two halves, discard the unnecessary, divide the rest again into two parts, and so until we find the desired value. This type of algorithm is called Divide and Conquer Divide and Conquer.

This algorithm is based on logarithm.
A quick overview of logarithms
Consider an example of what will be x?
x ^ 3 = 8
We need to take the cubic root of 8 - it will be 2. Now it is more difficult
2 ^ x = 512
Using logarithm, the problem can be written as
log2 (512) = x
“The logarithm of base 2 from 512 is x”. Note the “base 2”, i.e. we think in twos - how many times you need to multiply 2 to get 512.
In the “binary search” algorithm, at each step we divide the array into two parts.
My addition. Those. at worst, we do as many operations as we can divide the array into two parts. For example, how many times can we divide into two parts an array of 4 elements? 2 times. And an array of 8 elements? 3 times. Those. number of divisions / operations = log2 (n) (where n is the number of array elements).
It turns out that the dependence of the number of operations on the number of input elements is described as log2 (n)
Thus, using the Big O notation, the “binary search” algorithm has O (log n) complexity.
Improve O (n ^ 2) to O (n log n)
Let's return to the task of checking the array for doubles. We went through all the elements of the array and for each element we did another search. Did O (n) inside O (n), i.e. O (n * n) or O (n ^ 2).
We can replace the nested loop with a binary search. Those. we still have to iterate over all elements of O (n), inside we do O (log n). It turns out O (n * log n), or O (n log n).
const nums = [1, 2, 3, 4, 5]; const searchFor = function (items, num) { //use binary search! //if found, return the number. Otherwise... //return null. We'll do this in a later chapter. } const hasDuplicates = function (nums) { for (let num of nums) { //let's go through the list again and have a look //at all the other numbers so we can compare if (searchFor(nums, num)) { return true; } } //only arrive here if there are no dups return false; } Thinking in Big O terms
- Receiving a collection item is O (1) Whether it's getting by index in an array, or by key in a dictionary in Big O notation, it will be O (1)
- Search collection is O (n)
- Nested loops for the same collection are O (n ^ 2)
- Divide and Conquer always O (log n)
- Iterations that use Divide and Conquer are O (n log n)
Source: https://habr.com/ru/post/444594/
All Articles