Exotic pencil: detecting a second sound in ordinary graphite

Wake up in the morning with the singing of the toucans, see the weather forecast and see all the same +28, put on your favorite shorts and go for a walk around the city, ward off arrogant monkeys from the garbage can, walk along the palm avenue, sit on the bench in front of the lake and feed the flamingos, remember about the preparation for winter and buy some more shorts. For someone, such a day is not something unusual, but for us (I mean the inhabitants of the continental climate regions), this is a real exotic. What does the flamingos and toucans to physics, you ask? And despite the fact that physics is also not alien to the exotic, manifested in processes, substances and phenomena that somehow differ from the generally accepted norm. Today we will talk about one of these phenomena - the second sound, which was found in ordinary graphite. What is so exotic about it, how scientists have found it, and should we share their delight from the discovery? We will find the answers where there is usually no, not in Google, but in the report of the research group. Go.

Theoretical retreat

The second sound is a rather funny name of the phenomenon, which only indirectly refers to the sound itself (it is slightly in contact with it with its sleeves, so to speak). The second sound is a quantum-mechanical phenomenon in which heat transfer takes place in a wave-like, rather than the usual diffusion. The word "sound" is present in the name of this process due to the similarity of the wave heat propagation with a similar propagation of sound waves.
')
Sound waves represent fluctuations in the density of molecules in a substance, while second-sound waves are already fluctuations in the density of particle-like thermal excitations (phonons and rotons * ).

Roton * is a quasi-particle in superfluid ⁴ He (helium-4).

Earlier manifestations of the second sound were found in a rather small list of substances and at sufficiently low temperatures:

- ² He - liquid ( superfluid * ) helium, obtained by cooling 4He below 2.1768 K;

- ⁴ He, ³ He, Bi (bismuth) at a temperature of 1.2 ... 4.0 K and NaF (sodium fluoride) in a solid state of aggregation at a temperature of 10 ... 20 K.

Superfluidity * - the property of a fluid with zero viscosity, which allows it to flow without loss of kinetic energy. In other words, such a substance (quantum liquid) at temperatures close to absolute zero can pass through very narrow openings and capillaries without friction.

However, scientists have continued to search for a second sound in other substances. The search gave the result - signs of a second sound were found in ordinary graphite at temperatures above 100 K.

In their study, scientists used optical measurements of heat transfer in graphite with a scale length of 5-20 microns. The results of the observations are completely comparable with the calculations performed earlier and theoretically indicating the presence of a second sound on a ~ 1 μm scale at high temperatures (up to room temperature).

Researchers remind us that in ordinary non-metallic solids, heat is transferred by lattice vibrations or phonons * (not to be confused with photons). In an ideal (practically) crystal at a temperature of about 10 K, phonons can propagate to microscopic distances without scattering, and this leads to ballistic heat transfer.

Phonon * is a quantum of the vibrational motion of a crystal atom.

At room temperature, however, the average length of heat transfer for a phonon is rather small due to the high phonon-phonon scattering velocities; therefore, heat propagates due to diffusion over macroscopic distances.

The second sound, as a phenomenon, is located somewhere between the ballistic and diffusive heat transfer. This intermediate mode is called phonon hydrodynamics. In such a situation, normal phonon-phonon scattering proceeds much more often, in which the total reduced phonon momentum is preserved, and there is less often a transfer process * . Flipping processes * - when quasi-particles collide in crystals, and the law of conservation of momentum is realized to within the reciprocal lattice vector. However, normal scattering alone is not enough to dissipate heat flux and return the lattice to thermal equilibrium. Instead, the phonon population relaxes to the “shifted” Bose-Einstein distribution, which is characterized by a non-zero drift velocity, which is comparable to the flux of molecules in gases. This allows thermal waves (phonon density waves) to propagate at a speed lower than the speed of sound.

Research results

During the preparation for the actual experiments, scientists carried out calculations and familiarized themselves with some theoretical predictions made earlier. They found that the second sound should occur in the time interval between normal scattering and flipping (τ _N <t <τ _U ). In accordance with theoretical predictions for graphene, the nanosecond scale of the experiment was established. And this complicates the research process due to the inability to use conventional thermal sensors to determine heat transfer. Therefore, scientists turned to lasers for help. More precisely, the method of transitional thermal grids ( 1A ) was used, when two short (60 ps) laser pulses intersect on the sample surface.


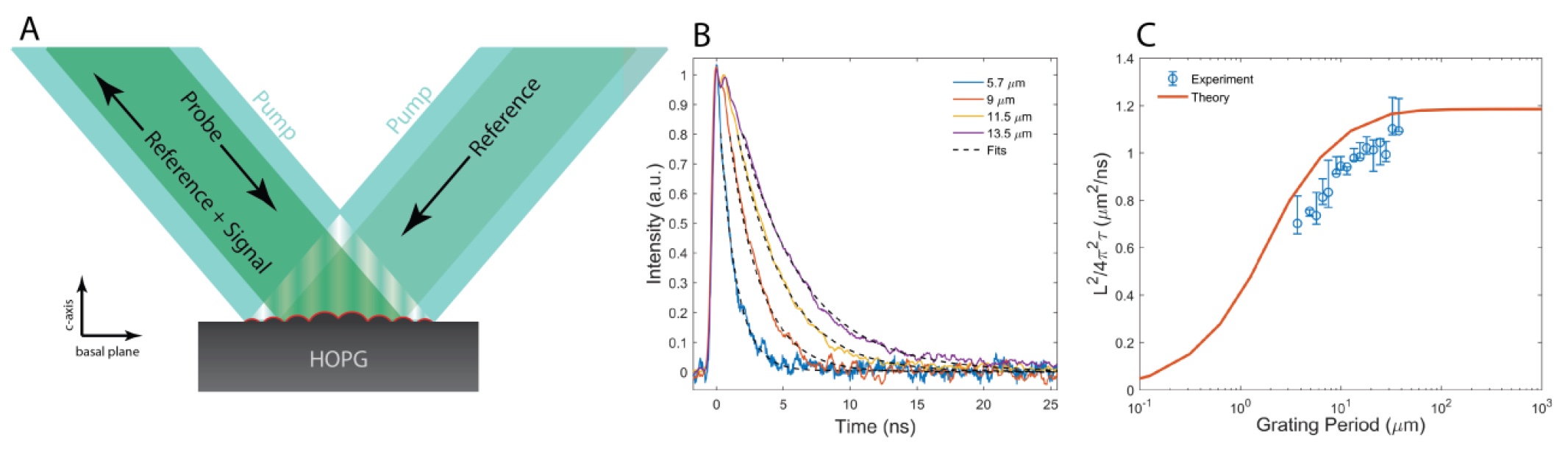
Image number 1

Laser “handshake” forms a spatially sinusoidal heat source, the period of which ( L ) is determined by the pattern of optical interference.

Due to thermal radiation, a “thermal lattice” is formed - a spatially sinusoidal temperature field along the sample surface (∆T (t, z) cos (qx), where q = 2π / L is the wave vector of the thermal lattice). Subsequently, due to heat transfer, this heat lattice disintegrates. Thermal expansion creates a coupled sinusoidal modulation of the surface displacement or “pulsation” u (t) cos (qx), which acts as a transient diffraction grating for laser radiation. Thus, the attenuation (decay) of the thermal lattice due to heat transfer is controlled by the time-dependent diffraction of the probe laser beam with a continuous wave. The diffracted beam is superimposed on the reference from the same source for optical heterodyne detection.

The main character of this study, that is, the sample, was made by highly oriented pyrolytic graphite. The sample was a polycrystal with a grain size of ~ 10 μm, and the axis position with all the grains was perpendicular to the surface of the sample itself.

Initially, a sample of 515 nm light was applied to the sample to create an initial thermal lattice at an optical skin depth of ~ 30 nm. The heat transfer process proceeded in two directions: along the surface of the thermal lattice (in the plane) and perpendicular to the surface (transverse plane). The heat transfer in the transverse plane of graphite was ~ 300 times weaker than the transfer in the plane. Thus, the depth of thermal diffusion in the transverse plane is much smaller than the position of the thermal lattice.

In accordance with the diffusion of heat (τ = L ² / 4π ² ), in a one-dimensional medium, the decay of the transition thermal lattice occurs exponentially. This statement was confirmed in practice: at a temperature of 300 K, signs of exponential decay ( 1B ) were found. At L (lattice period) equal to 37.5 μm, the thermal diffusivity of 11 cm ² / s was obtained.

With a decrease in the lattice period, the heat diffusion formula given above does not correspond to a constant value of ⍺ (thermal diffusivity). The smaller the lattice period, the slower the decay / attenuation of the transitional thermal lattice ( 1C ). This is at variance with the predictions of the diffusion model of heat transfer.


Image number 2

Graph 2A shows significant changes when the temperature drops to 85 K. At a temperature of 300 K, the signals attenuate monotonous, but at 85 K, damped oscillations occur when the signal can drop below zero. For heterodyne detection, a change in the sign of the transient thermal lattice signal means that the spatial phase of the lattice has shifted by π. In other words, the position of local maxima and minima of surface displacements (including temperatures) changed places. And this behavior of the transitional thermal lattice is comparable to the thermal standing wave * .

Standing wave * is a wave process in distributed oscillatory systems with alternating and space-stable maxima and minima of amplitude.

In the diffusion variant, heat transfer occurs from hotter to colder regions, and the maxima and minima cannot be swapped. That is, this observation is a distinctive feature of the wave heat distribution.

Insertion in Graph 2A shows that with an increase in the lattice period, the frequency of the wave-like dynamics decreases. The observed linear relationship indicates a speed of 3200 m / s. This is an important observation, since the signals of the transitional thermal lattice can often contain vibrations due to surface acoustic waves, but their speed is much lower. Considering that the speed of surface acoustic waves is approximately 1480 m / s, which is close to the indices of a slow transverse velocity, whereas the fast transverse velocity is 14700 m / s, and the longitudinal velocity is even higher. It is also worth noting that if the acoustic waves were, they would not disappear with an increase in the background temperature or the grating period.

In order to simulate such dynamics, scientists applied the linearized Boltzmann transport equation with a full three-phonon scattering matrix in a one-dimensional transitional thermal lattice. Previously, a similar method was used to determine the thermal conductivity of graphene and graphite. However, this technique was somewhat limited and could not be applied if it were not for the new research, which described the method for calculating the frequency Green's functions for the unsteady and inhomogeneous Boltzmann transfer. Graph 2B shows precisely these Green functions, which describe the response of a phonon population to a heat source, which has the shape of a harmonic plane wave.

The calculations carried out by scientists taking into account the above methods made it possible to understand the time dependence of the amplitude of the thermal lattice. Calculations at a temperature of 300 K and various lattice periods showed an exponential decay of the transition thermal lattice, which is fully consistent with the experiment ( 1C ). At a temperature of 85 K, the Green's frequency function gives a resonant peak ( 2B ), which is a distinctive feature of the second sound and causes attenuation fluctuations ( 2C ). All calculated data are completely comparable with experimental data - even the fact of the disappearance of a second sound at large periods of a transitional thermal lattice.

Calculations showed that the speed of the second sound (given the position of the peak of the resonance frequency at 2C ) is 3650 m / s. Such an indicator distinguishes graphite from a number of other materials where a second sound was detected. In them, the speed of the second sound was slower than the minimum speed of the phonons. Graphite is also amazing because it has a very low speed of a slow transverse acoustic mode. And the impressive anharmonicity and density of states of this mode lead to intense normal scattering and create conditions for the hydrodynamic transfer of phonons.


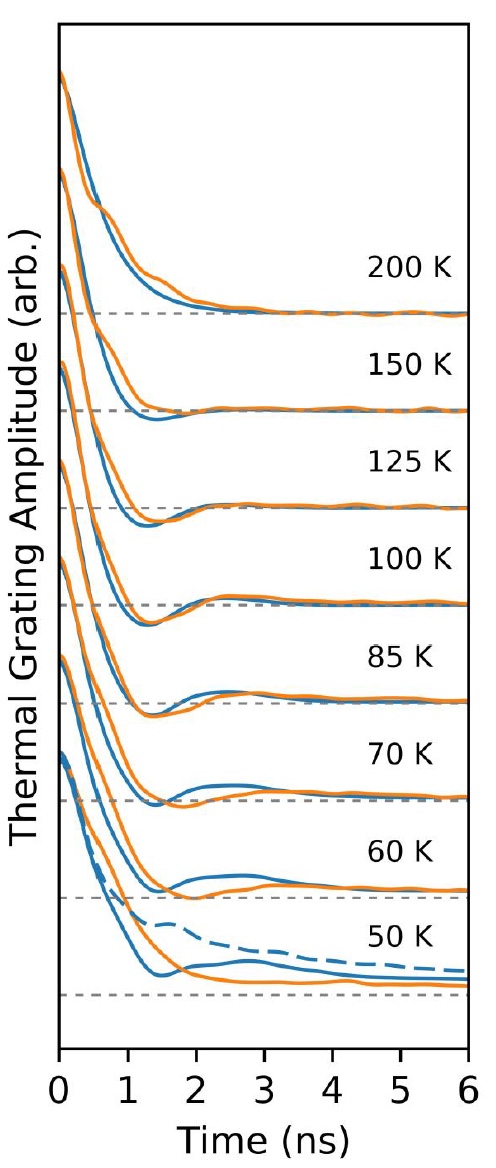
Image number 3

The graph above ( # 3 ) displays the data of the transitional thermal lattice at a constant period of 10 μm and at different temperatures. Oscillatory behavior was observed at 104 K and even at 125 K, but when the temperature reaches 150 K, it completely disappears. The same thing happens when the temperature drops below 50 K.

The graph also shows the simulated response at 50 K in the ballistic mode, when the phonon scattering rate was set to zero. And here it is clear that the failure in the response in the ballistic regime disappears. That is, the disappearance of the second sound at a temperature of 50 K corresponds to what is expected during the transition to the ballistic regime.


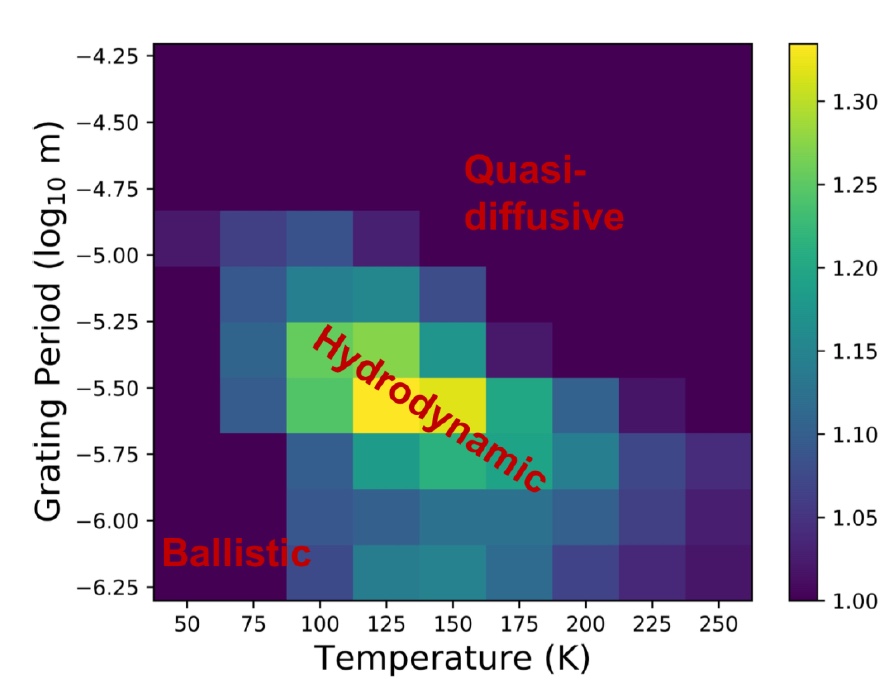
Image number 4

Data modeling has shown that the occurrence of a second sound can be expected in the temperature range from 50 to 250 K. The higher the temperature, the shorter the heat transfer length: at L = 10 μm, the temperature “ceiling” is about 150 K, but already at L = 1.5 μm The second sound will be observed up to 250 K.

At low temperatures and small lattice periods, phonon scattering disappears, and heat transfer becomes ballistic. If there are high temperatures and long periods, the heat transfer slowly goes into a “quasi-diffusion” mode.

Graphite is also distinguished in terms of isotopes. That is, previously the second sound was observed only in isotopically pure solids (if you do not take into account the controversial, according to scientists, observations in SrTiO ₃ ). But the graphite used in the experiment is not isotopically pure, which indicates the unique nature of the phonon hydrodynamics of this substance.

For more detailed acquaintance with the nuances, details, methodology and calculations of the study I strongly recommend to look into the report of scientists and additional materials to it.

Epilogue

Sometimes exotic phenomena or properties are hidden in the most ordinary and unremarkable objects. This study was proof of that. The second sound, being an exotic phenomenon, was previously observed only in very “strange” substances and under very extreme conditions.

Scientists consider their work to be important for a general study of phonon hydrodynamics. Understanding such things will make it possible to use graphite and graphene as heat-scattering materials in microelectronics. Also, scientists believe that their work will accelerate the study of manipulation and control over transport processes in the micro and nano scale.

We know so much about the things around us, but at the same time, such studies suggest the opposite. Is there a limit to this knowledge? While there is curiosity and enthusiasm of scientists - no.

Thank you for your attention, remain curious and have a good working week, guys.

Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending to friends, 30% discount for Habr's users on a unique analogue of the entry-level servers that we invented for you: The whole truth about VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps from $ 20 or how to share the server? (Options are available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps before summer for free if you pay for a period of six months, you can order here .

Dell R730xd 2 times cheaper? Only we have 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV from $ 249 in the Netherlands and the USA! Read about How to build an infrastructure building. class c using servers Dell R730xd E5-2650 v4 worth 9000 euros for a penny?