Mathematics, reconciling Newton with the quantum world

As a professor of mathematics, he stopped being afraid and fell in love with algebraic geometry.

At the sixth dozen it is already too late to become a real expert in algebraic geometry, but I finally managed to fall in love with her. As its name implies, this branch of mathematics uses algebra to study geometry. Around 1637, Rene Descartes laid the foundation for this area of ​​knowledge, taking a plane, mentally drawing a grid on it and marking the coordinates for x and y . You can write an equation of the form x ² + y ² = 1, and get a curve consisting of points whose coordinates satisfy this equation. In this example we will get a circle.

For that time, it was a revolutionary idea, because it allows us to systematically convert geometry questions into equations questions, which, with sufficient knowledge of algebra, can be solved. Some mathematicians have been engaged in this magnificent field all their lives. I didn’t like it until recently, but I was able to connect it with my interest in quantum physics.

In childhood I liked physics more than mathematics. My uncle Albert Baez, father of the famous folk singer Joan Baez, worked for UNESCO and helped developing countries with teaching physics. My parents lived in Washington. When my uncle came to town, he opened his briefcase, took out magnets or holograms from there, and with their help explained physics to me. It was awesome. When I was eight years old, he presented me with a physics textbook for college. Although I could not understand him, I immediately realized that I wanted this. I decided to become a physicist, and my parents were worried, because they knew that physics needed mathematics, and I was not very strong in it. Dividing the bar seemed unbearably boring, and I refused to do the math homework with its endlessly repetitive routine. But later, when I realized that, playing with equations, I could learn more about the Universe, it fascinated me. Mysterious characters were like magic spells, and in a sense it was so. Science is magic that actually works.
')
In college, I chose mathematics as the main subject, and I became interested in the question of the theoretical physicist Eugene Wigner about the "inexplicable efficiency" of mathematics: why does our Universe so readily obey mathematical laws? He put it this way: "The miracle of the adequacy of the language of mathematics for the formulation of the laws of physics is a delightful gift that we do not comprehend and do not deserve." Being a young optimist, I felt that these laws would give us hints for solving a deeper puzzle: why the Universe is generally governed by mathematical laws. I already understood that mathematics is too voluminous to study it entirely, therefore in the magistracy I decided to focus on what was important to me. And one of those that did not seem important to me was algebraic geometry.

How can a mathematician not fall in love with algebraic geometry? The reason is the following: in its classical form, this area examines only polynomial equations - equations that describe not just curves, but also figures of higher dimension, called "manifolds". That is, x ² + y ² = 1 - this is normal, as is x ⁴³ - 2 xy ² = y ⁷ . But the equation with sines, cosines, or other functions is outside this area, unless we find some way to convert it into an equation from polynomials. To the graduate student this seemed a terrible restriction. In the end, the problems of physics use a variety of functions that are not polynomials.


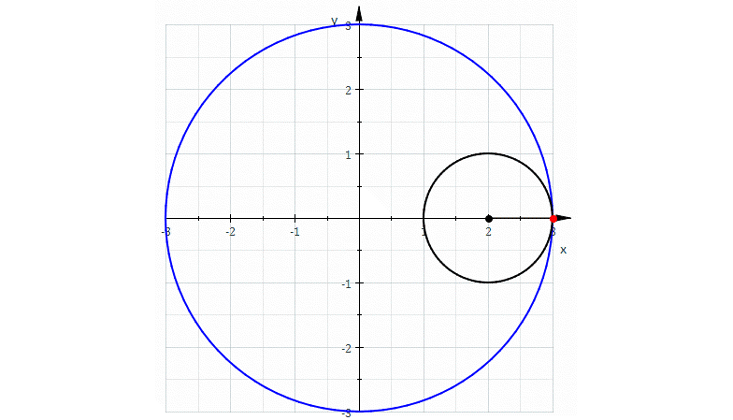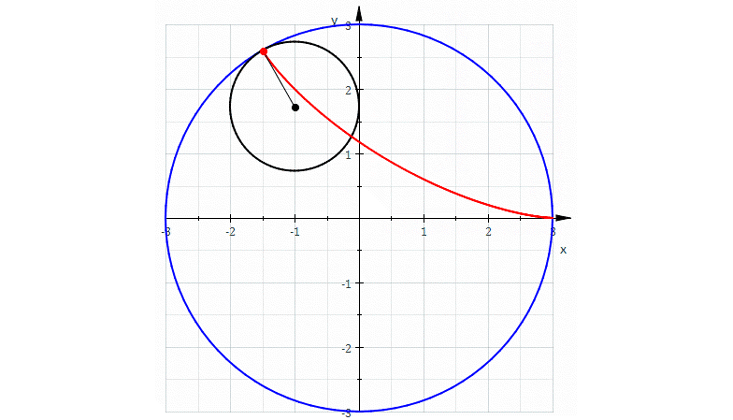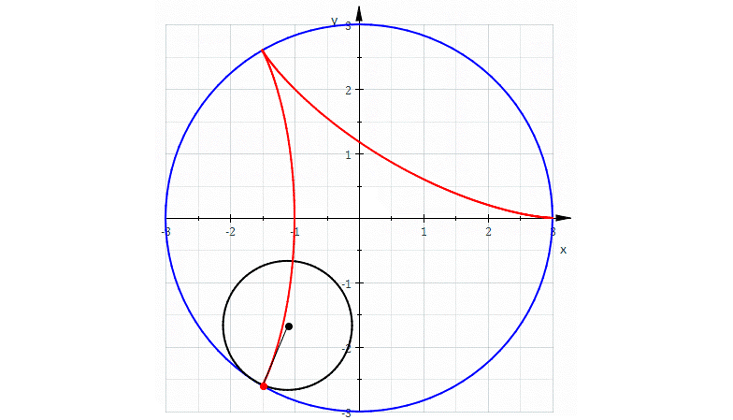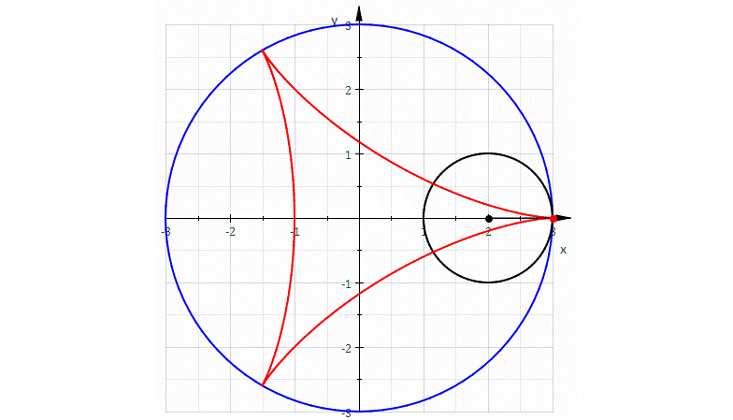
For this there is a polynomial: with the help of some polynomials one can describe a lot of interesting curves. For example, let's roll a circle inside another circle, three times the size. We obtain a curve with three sharp corners, which is called the "deltoid". It is not obvious that it can be described by a polynomial equation, but it is. The great mathematician Leonard Euler invented it in 1745.

Why does algebraic geometry limit itself to polynomials? Mathematicians study all sorts of functions, but although they are very important, at some level their complexity only distracts from the fundamental mysteries of the connection between geometry and algebra. By limiting the width of their searches, algebraic geometry can explore these riddles deeper. She has been doing this for centuries, and now the skill of working with polynomials is truly amazing: algebraic geometry has become a powerful tool in number theory, cryptography and many other fields. But for her true admirers, the value of this field lies in itself.

Once I met a graduate student from Harvard and asked him what he was studying. In a pompous tone, he said one word: "Hartshorn." He was referring to the textbook by Robin Hartshorn "Algebraic Geometry" , published in 1977. It is assumed that it should be an introduction to the subject, but in fact is very complex. Let us quote the description from Wikipedia: “The first chapter entitled“ Varieties ”tells about the classical algebraic geometry of varieties over algebraically closed fields. This chapter uses a variety of classical results from commutative algebra, including Hilbert's theorem on zeros, and often references are made to the books of Atiyah-Macdonald, Matsumura and Zarissky-Samuel. ”

If you don't understand anything ... then that is what I meant. To understand even the first chapter of Hartshorn, you need a fairly large amount of background knowledge. Reading Hartshorn is like trying to catch up with the geniuses of many centuries who have tried to flee.


Famous Cubic: This is Cayley's cubic knot surface. It is famous for the fact that it is a manifold with the largest number of nodes (such sharp pieces) that can be described by a cubic equation. The equation has the form ( xy + yz + zx ) (1 - x - y - z ) xyz = 0 and is called “cubic” because at the same time we multiply no more than three variables.

One of these geniuses was the academic director of Hartshorn - Alexander Grothendieck. From about 1960 to 1970, Grothendieck made a revolution in algebraic geometry, making it part of an epic journey in order to prove Weil's hypotheses connecting varieties with solutions to problems from number theory. Grothendieck suggested that Weil's hypotheses can be confirmed by strengthening and deepening the connection between geometry and algebra. He had a clear idea of ​​how this should happen. But to ensure the accuracy of this idea required a lot of work. To carry it out, he organized a seminar. Grothendieck made reports almost every day and used the help of the best mathematicians in Paris.


Let's run the mat: von Alexander Grothendiek at his seminar.

Working endlessly for a decade, they wrote thousands of pages of new mathematics, filled with stunning concepts. In the end, taking advantage of these ideas, Grothendieck successfully proved all of Weyl's hypotheses, except the last, the most difficult one. To Grothendick’s surprise, it was decided by his student.

During his most productive years, even despite the dominance of algebraic geometry in the French school, many mathematicians considered Grothendieck’s ideas “too abstract.” It sounds a bit strange, considering how abstract all mathematics is. But undoubtedly, it takes time and effort to perceive his ideas. As a graduate student, I tried to distance myself from them, because I actively fought with the study of physics: in it geniuses also worked at full speed for centuries, and in order to get to the front line, you have to catch up with a lot. But later, when I began my career, my research led me to the work of Grothendieck.

If I chose another way, I could approach his work through the study of string theory . Physicists studying string theory postulate that in addition to the visible dimensions of space and time (three dimensions for space and one for time), there are additional dimensions of space that are so twisted that they cannot be seen. In some of their theories, these extra dimensions form a manifold. Therefore, string theory researchers can easily encounter complex questions from algebraic geometry. And this, in turn, makes them run into Grothendik.


I'm completely confused: a slice of a single manifold, called the "fifth-dimensional three-dimensional manifold" (quintic threefold), which can be used to describe additional convoluted dimensions of space in string theory.

And in fact. Best of all, string theory does not advertise the successful prediction of experimental results — it absolutely cannot boast of this — but the ability to solve problems within pure mathematics, including algebraic geometry. For example, string theory is amazingly good at counting the number of different kinds of curves that can be drawn in certain varieties. Therefore, today one can see string theorists communicating with algebraic geometers, and each side can surprise the other with its own discoveries.

But the source of my personal interest in the work of Grothendieck was different. I have always had serious doubts in string theory, and counting curves in manifolds is the last thing I want to do: it's like climbing to watch it, but it's too scary to do it yourself. It turned out that Grothendieck’s ideas are as general and strong as they are that they extend beyond the limits of algebraic geometry to many other areas. In particular, I was impressed by his 600-page unpublished manuscript of Pursuing Stacks , written in 1983. In it, he states that topology (if to explain in a broad sense, this theory about what forms space can take, if we are not concerned with its bending or stretching, but only the types of holes are interested) can be entirely reduced to algebra!

At first, this idea may seem similar to algebraic geometry, in which we use algebra to describe geometric figures (for example, curves or varieties of higher dimensions). But it turns out that the “algebraic topology” has a completely different flavor, because in topology we are not obliged to limit ourselves to the figures described by polynomial equations. Instead of working with beautiful jewels, we are dealing with flexible, soft clots; so we need another algebra.


If an explanation is needed: mathematicians sometimes joke that topologists do not see the difference between a donut and a cup of coffee.

Algebraic topology is a beautiful area that existed long before Grothendieck, but he was one of the first to seriously suggest a method of reducing the whole topology to algebra. Thanks to my work in physics, his proposal seemed to me extremely delightful. And here's why: at that moment I took on the difficult task of combining the two best theories of physics: quantum physics, which describes all forces except gravity, and the general theory of relativity, which describes gravity. It seems that until we do this, our understanding of the fundamental laws of physics is doomed to be incomplete. But it's damn hard to implement. The reason is that quantum physics is based on algebra, and topology is actively used in the general theory of relativity. But this tells us the direction of the attack: if we can figure out how to reduce topology to algebra, then this may help us formulate a theory of quantum gravity.

My colleagues-physicists at this moment would howl and began to complain that I am simplifying too much: in quantum physics, not just algebra is used, but the general theory of relativity is not only topology. Nevertheless, it was precisely the possible physical advantages of reducing topology to algebra that delighted me in Grothendieck’s work.

Therefore, starting from the 1990s, I tried to understand the powerful abstract concepts invented by Grotendik, and today I have achieved partial success. Some mathematicians consider these concepts to be a complex part of algebraic geometry. But now they seem to me the easy part. For me, not all of these abstract concepts have become a difficult part, but their boring details. Firstly, this is all the material in the texts that Hartshorn considers mandatory prerequisites: “the books of Attias-Macdonald, Matsumura and Zarissky-Samuel”, and these are huge volumes of algebra. But there is more.

Therefore, although I now have part of what is needed to read Hartshorn, until recently, the study of these materials too frightened me. A physics student once asked a famous specialist how much mathematics a physicist should know. The specialist replied: "More than he knows." Indeed, the study of mathematics can never be considered complete, so I focused on aspects that seemed most important and / or interesting. Until last year, algebraic geometry never appeared at the beginning of this list.

What has changed? I realized that algebraic geometry is related to the relationship between classical and quantum physics . Classical physics is Newton's physics, in which we assume that we can measure everything with complete accuracy, at least in theory. Quantum physics is the physics of Schrödinger and Heisenberg, and it is governed by the uncertainty principle: if we measure certain aspects of a physical system with complete accuracy, others must remain undefined.

For example, any rotating object has an angular momentum. In classical mechanics, we visualize it with an arrow directed along the axis of rotation, and the length of this arrow is proportional to the speed of rotation of the object. And in classical mechanics, we assume that we can accurately measure this arrow. In quantum mechanics — a more accurate description of reality — this turns out to be wrong. For example, if we know how far the arrow points in the x direction, we cannot find out. how far it points in the y direction. This uncertainty is too small to notice for a basketball, but for an electron it is very significant: until physicists started to take this into account, they had only a rough understanding of electrons.

Physicists often seek to “quantify” the problems of classical physics. That is, they begin with the classical description of a physical system and try to derive a quantum description. There is no general and completely systematized procedure for this work. And this should not surprise you: these two world views are very different. However, there are useful recipes for quantizing. The most systematic of them are applicable to a very limited set of physical problems.

For example, in classical physics, we can sometimes describe a system with a point in a manifold . You should not expect that this is possible in the general case, but in many important cases this happens. For example, consider a rotating object: if we fix the length of the arrow of its angular momentum, then the arrow can still point in any direction, that is, its end must lie on the sphere. Thus, we can describe a rotating object as a point on the sphere. And this sphere is in fact a variety, the “ Riemann sphere ”, named after one of the greatest algebraic geometers of the 19th century, Bernhard Riemann.


Variety: The eighth-order surface of Endrass is a beautiful, highly symmetric example of a “manifold”: a figure described by polynomial equations. Algebraic geometry began as a study of such figures.

When the task of classical physics is described by diversity, magic happens. The quantization process becomes completely systematic and surprisingly simple. There is even a kind of inverse process, which can be called "classification" - it allows you to convert a quantum description back into a classical description. Classical and quantum approaches to physics become closely related, we can take ideas from any approach and watch what they can tell us about something else. For example, each point in a manifold describes not only the state of the classical system — in our example, this particular direction of the angular momentum — but also the state of the corresponding quantum system, even though the latter is governed by the Heisenberg uncertainty principle. The quantum state is the “best quantum approximation” to the classical state. Moreover, in this situation, many basic theorems from algebraic geometry can be considered as facts about quantization. Since I have been engaged in quantization for a long time, this makes me extremely happy.

Richard Feynman once said that in order to advance in solving a complex physical problem, he needed to look at it from a particular angle:

"[...] I need to think that I have some kind of shortest way to solve the current problem. That is, it’s as if I have a talent that others don’t use, or a special view, which they foolishly didn’t consider to be an excellent look at things. I need to think that for some reason my chances are higher than that of others. In my heart I know that most likely this reason is false, and most likely my view has already been used by others. But I don’t care: I am deceiving myself, convincing me that I have an extra chance. "

Perhaps this is what I lacked until recently in algebraic geometry. Of course, algebraic geometry is not just a task that needs to be solved, but a complex of knowledge — but it is such a huge, frightening set that I did not dare touch it until I found this shortest path. Now I can read Hartshorn, translate some of the results into facts about physics, and I have a chance to understand all this. This is an excellent feeling.

About the author : John Baez is a professor of mathematics from the University of California at Riverside and a visiting researcher at the Center for Quantum Technologies in Singapore. He runs an Azimuth blog about math, science and environmental issues. Follow him on Twitter: @johncarlosbaez .