The book "The perfect algorithm. Basics

Hi, Habrozhiteli! This book is based on online courses on algorithms that Tim Rafgarden leads on Coursera and Stanford Lagunita, and these courses have appeared thanks to lectures for students that he has been teaching at Stanford University for many years.

Algorithms are the heart and soul of computer science. You can't do without them, they are everywhere - from network routing and genomics calculations to cryptography and machine learning. The “perfect algorithm” will turn you into a real pro, who will set tasks and masterfully solve them both in life and during an interview when applying for a job at any IT company. Tim Rafgarden will talk about asymptotic analysis, big-O notation, divide-and-rule algorithms, randomization, sorting and selection. The book is written for those who already have programming experience. You will go to a new level to see the big picture, to understand low-level concepts and mathematical nuances.

* 6.3. Algorithm DSelect

The RSelect algorithm runs in linear time for each input, in which the expectation is associated with random choices performed by the algorithm. Is randomization required for linear selection? In this section and further, this problem is solved using a deterministic linear algorithm for the selection problem.

For the sorting problem, the average running time O (n log n) of the randomized QuickSort algorithm coincides with the running time of the deterministic MergeSort algorithm, and both the QuickSort and MergeSort algorithms are useful algorithms for practical use. On the other hand, although the deterministic linear selection algorithm described in this section works fine in practice, it does not compete with the RSelect algorithm. This happens for two reasons: due to the large constant factors in the operation time of the DSelect algorithm and the work performed by the algorithm related to the allocation and management of additional RAM. Nevertheless, the ideas in the algorithm are so cool that I can not tell you about them.
')

6.3.1. Brilliant idea: median median

The RSelect algorithm is fast because there is a high probability that random support elements will be quite good, providing an approximately balanced partitioning of the input array after separation, and moreover, fairly good support elements are rapidly progressing. If we are not allowed to use randomization, how can we compute a fairly good reference element without doing too much work?

A brilliant idea in a deterministic linear choice is to use the median median as a proxy for the true median. The algorithm considers the elements of the input array as sports teams and holds a knockout tournament in two rounds, the champion of which is the supporting element; see also fig. 6.1.


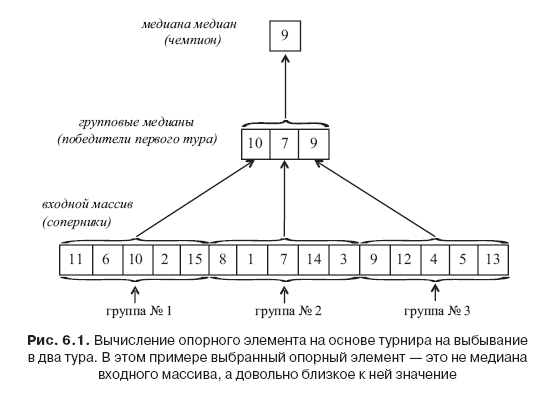
The first round is a group stage with elements in positions 1–5 of the input array as the first group, elements in positions 6–10 as the second group, and so on. The winner of the first round of a group of five elements is defined as the median of the element (that is, the third smallest). Since there is 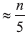groups of five elements, there are 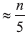first winners. (As usual, we ignore fractions for simplicity.) A tournament champion is defined as the median of the winners of the first round.

6.3.2. Pseudocode for DSelect algorithm

How to actually calculate the median median? The implementation of the first stage of the knockout tournament is simple, since each calculation of the median includes only five elements. For example, each such calculation can be performed by a search method (for each of the five possibilities, check in detail whether it is a middle element) or using our information to the sorting problem (section 6.1.2). To implement the second stage, we calculate the median of 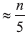The winners of the first round are recursive.


Lines 1–2 and 6–13 are identical to the RSelect algorithm. Lines 3–5 are the only new part of the algorithm; they calculate the median of the median of the input array, replacing the string in the RSelect algorithm, which selects the reference element at random.

Lines 3 and 4 calculate the winners of the first round of the knockout tournament, where the middle element of each group of five elements is calculated using the search method or the sorting algorithm, and these winners are copied to the new array C. Line 5 calculates the tournament champion by recursively calculating the median of array C; since C has a length (approximately) 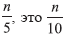-th ordinal statistics of array C. No randomization is used at any step of the algorithm.

6.3.3. Understanding the DSelect algorithm

Recursively calling the DSelect algorithm when calculating a reference element may seem dangerously cyclical. To understand what is happening, let's first designate the total number of recursive calls.


The correct answer is: (c). Dropping the base case and the lucky case, in which the reference element is the required ordinal statistics, the DSelect algorithm makes two recursive calls. To understand why, do not be too smart; just check the pseudo-code DSelect algorithm line by line. In line 5 there is one recursive call and one more in line 11 or 13.

There are two confusing common questions about these two recursive calls. First, is it not the fact that the RSelect algorithm makes just one recursive call, the reason why it works faster than our sorting algorithms? Doesn't DSelect reject this improvement by making two recursive calls? Section 6.4 shows that since the additional recursive call in line 5 should solve only a relatively small subtask (with 20% of the elements of the original array), we can still save the linear analysis.

Secondly, two recursive calls play fundamentally different roles. The purpose of the recursive call in line 5 is to determine a good reference element for the current recursive call. The purpose of a recursive call on line 11 or 13 is simple — to recursively solve the smaller remaining problem left by the current recursive call. However, the recursive structure in the DSelect algorithm follows the tradition of all the other divide-and-conquer algorithms we studied: each recursive call makes a small number of subsequent recursive calls with strictly smaller subtasks and does some additional work. If we didn’t worry that algorithms like MergeSort or QuickSort would run forever, we wouldn’t have to worry about the DSelect algorithm either.

6.3.4. DSelect algorithm time

The DSelect algorithm is not just a clearly formulated program that ends in a limited amount of time — it runs in linear time, doing more work only on a constant factor than is needed to read the input data.

Theorem 6.6 (time of the DSelect algorithm). For each input array of length n ≥ 1, the running time of the DSelect algorithm is O (n).

Unlike the operation time of the RSelect algorithm, which in principle can be no more than Θ (n2), the operation time of the DSelect algorithm is always O (n). However, in practice, you should prefer RSelect to DSelect, because the former works in the same place, and the constant hidden in the average O (n) operation time in Theorem 6.1 is less than the constant hidden in Theorem 6.6.

»More information about the book can be found on the publisher's website.
» Table of Contents
» Excerpt

For Habrozhiteley a 20% discount on the coupon - Algorithms

Upon payment of the paper version of the book, an electronic version of the book is sent to the e-mail.

PS: 7% of the cost of the book will go to the translation of new computer books, a list of books submitted to the printing press here .