Does speed reduce speed reduction?

Not so long ago, discussions were launched on the introduction of a fine for speeding at more than 10 km / h from the allowed. Traditionally for the Internet, they are conducted unconstructively , so I generally do not support any side of such holivar.
Arguments of car owners in the mass come down to the “I need” gnaws, which, of course, are not identical. A significant proportion of people who are forced to go to work 50 km every day through locations not covered by public transport account for no less than those driving by car to the bakery, which can be clearly seen from these cars left in the morning at home little snow.
')
On the part of urbanists, quite one-sided arguments are often heard, hackneyed private examples of European countries, whose population is sometimes completely comparable with the daily Moscow traffic, techniques like offensive cliches about “bydlopovozki”.
And when such a situation occurs, there is nothing better than discarding other people's emotions and invoking two impartial assistants - Matan and Python.
The weakness of the position of car owners - they do not put forward ways to solve their problems (in my opinion, the solution would be to eliminate the spontaneous development of every free piece of land in major cities and the development of regions so that people do not have to deal with labor migration to their capital in their home country such as to offer such things?). Urbanists always have a set of arguments and ready-made solutions, backed up by data. But sometimes these are studies of serious institutions, sometimes they are not very clear statistics without adequate rationing. These data in most cases, pushing the idea of a general decrease in the speed of movement in cities. And the most frequent argument in its favor is:
“All the same, because of the traffic lights, you cannot always move at the maximum speed, your average speed will be lower than the allowed one, so why not reduce the bit allowed?”
“Hmmm,” I always thought about this argument. If you reduce the maximum allowed, the average will also fall a little. And what does this prove - that it can be lowered again? What kind of aporia is this? We need to check how true this is.
I would like to present a further article with reservations to direct its criticism in the comments in a constructive way:
- Yes, I know how ugly the code is written, but it is more important for me that it worked correctly, I myself am not a programmer, it’s better to write remarks on the code in a personal.
- Yes, I know that the simulation could be made more difficult, fuller and more realistic. Only I will not accept the accusations that there is no change in traffic density during the day, different dynamics of different cars, weather conditions,
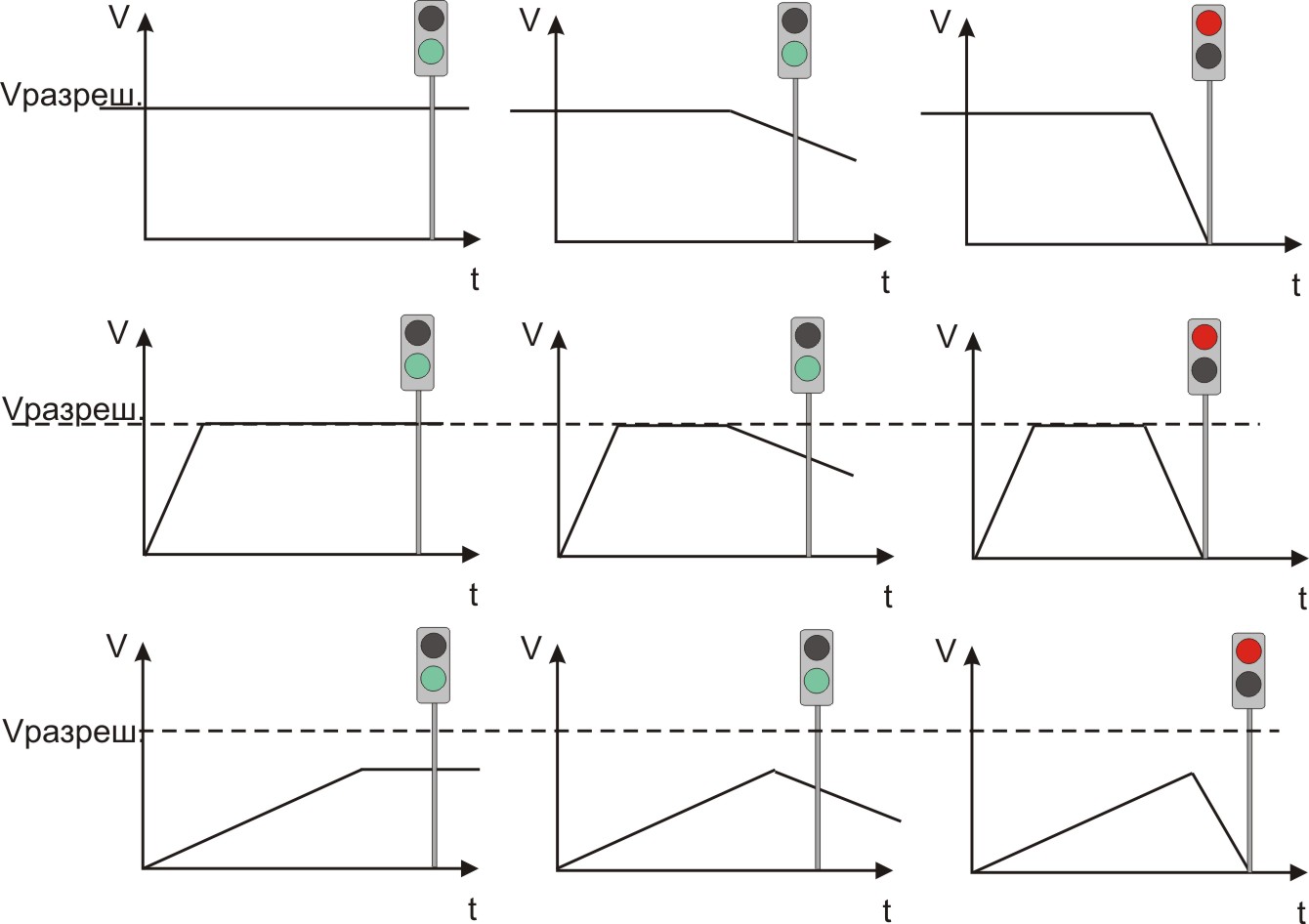
The essence of my model is very simple. Since the traffic light is a ready program cycle, the simulation is built around a segment of the road with a traffic light at the end and its phases. The next iteration is the next segment of the route with its length, allowed speed, and the phase of the traffic light at the end.
The car has three phases of motion: uniformly accelerated, motion with the maximum speed allowed for a given section, equally slow. They are implemented in 9 versions.
- If the car moved to the current segment at the same speed that is allowed on it, then it moves without changes;
- If he was moving slower (or standing), then he accelerates first;
- There is no “he moved faster” option, and here's why: if the allowed speed on the next segment is less, it reduces speed on it. Is it logical
These options are added more conditions:
- The car goes as driving or slowed down, and comes to the end of the segment to red. This means that we must stop at the traffic light. Assuming that it always slows down with the same acceleration, we postpone the way necessary for braking from the traffic light. This is a critical distance, similar to the critical take - off speed of aircraft. Now, if under the terms of the car passes through a red light, it should begin to brake to zero, starting from the critical point;
- Damn, or maybe the segment is so short or the car is so vegetable that it does not have time to pick up the maximum speed before the onset of Skrit? A program baganet, continuing to overclock it, although it is time for him to slow down before the traffic light? If this happens, we will force him not to pick up speed higher than that achieved at point Scrit, and then we will implement one of the options. Here is the result:
And then you need to implement it in the code. That's how I did it, providing detailed comments:
pattern of hinduism
import random import math # : redlight = ("100", "10", "90", "1", # "-" . . 1 "1") # 1 , 0. . . # : greenlight = ("30", "120", "30", "1", "1") # : distance = ("400", "400", "250", "500", "500") # velocity = ("60", "60", "60", "60", "40") #- r=0 g=0 d=0 v=0 # : vcurrent=float(0) # : t=0 # : gtime=0 #, 100 / 15 . # : accel=float(100/(3.6*15)) #, . # : decel = float(accel*2) # , ( , 0): while r<=2: red=float(redlight[r]) grn=float(greenlight[g]) dis=float(distance[d]) vel=float(float(velocity[v])/3.6) vnext=float(float(velocity[v+1])/3.6) # accel : #saccel = float(((vcurrent*vel-vcurrent)/accel) + ((vel-vcurrent)*((vel-vcurrent)/(2*accel) saccel = float((vcurrent*(vel-vcurrent)/accel) + (vel-vcurrent)*(vel-vcurrent)/(2*accel)) # : , decel: scrit = float(dis-(vel/decel) - (vel*vel)/(2*decel)) # , . # : startingred = random.randint(0, (int(grn)-1)) print ("startingred= ", startingred) # , __ - : if vcurrent == vel: # , , : if vnext>= vcurrent: t = int (dis/vel) # , : if (t+startingred)%(red+grn)<=red: t = int (scrit/vel + (vel/decel) + red-((t+startingred)%(red+grn))) ### 2 vcurrent = 0 print (" , ") # , : else: t = int (dis/vel)### 1 vcurrent = vel print (" , ", " v=", vcurrent) # , , scrit: else: t = int ((scrit/vel) + (vcurrent - (vnext)/((vcurrent*(vcurrent - (vnext/(dis-scrit))- ((vcurrent - vnext)*(vcurrent - vnext)/(2*(dis-scrit)))))))) # , : if (t+startingred)%(red+grn)<=red: t = int (scrit/vel + (vel/decel)+ red-((t+startingred)%(red+grn)))### 2 vcurrent = 0 print (" , ") # - , , scrit : else: t = int (scrit/vel + (vcurrent - vnext)/((vcurrent*(vcurrent - (vnext/(dis-scrit))- ((vcurrent - vnext)*(vcurrent - vnext)/(2*(dis-scrit)))))))### 3 vcurrent = float(vnext/3.6) print (" , ", " v=", vcurrent) # , __ - : elif vcurrent < vel: # , scrit: vcrit=math.sqrt(2*accel*scrit+vcurrent*vcurrent) # scrit, scrit, vcrit , : if saccel >= scrit: # - , if vnext >= vcrit: t = int(((vcrit-vcurrent)/ accel) + (dis-scrit)/vcrit) # , : if (t+startingred)%(red+grn)<=red: t = int(((vcrit-vcurrent)/ accel) + ((dis-scrit)*2/vcrit) + red-((t+startingred)%(red+grn)))### 8 vcurrent = 0 print (" , , ") # , : else: t = int(((vcrit-vcurrent)/ accel) + (dis-scrit)/vcrit) ### 7 vcurrent = vcrit print (" , , ", " v=", vcurrent) # - else: t = int(((vcrit-vcurrent)/ accel) + (vcrit - vnext)/((vcrit*(vcrit - vnext)/(dis-scrit))- ((vcrit - vnext)*(vcrit - vnext)/(2*(dis-scrit))))) # , : if (t+startingred)%(red+grn)<=red: t = int(((vcrit-vcurrent)/ accel) + ((dis-scrit)*2/vcrit) + red-((t+startingred)%(red+grn)) ) ### 8 vcurrent = 0 print (" , , ") # - , , scrit : else: t = int(((vcrit-vcurrent)/ accel) + (vcrit - vnext)/((vcrit*(vcrit - vnext)/(dis-scrit))- ((vcrit - vnext)*(vcrit - vnext)/(2*(dis-scrit))))) ### 9 vcurrent = vnext print (" , , ", " v=", vcurrent) # scrit, , : else: # , , : if vnext>= vel: t = int(((vel- vcurrent)/accel) + (dis-saccel)/vel) # , : if (t+startingred)%(red+grn)<=red: t = int (((vel- vcurrent)/accel) + (scrit-saccel)/vel + (vel/decel)+ red-((t+startingred)%(red+grn)))### 5 vcurrent = 0 print (" , ") # , : else: t = int (((vel- vcurrent)/accel) + (dis-saccel)/vel)### 4 vcurrent = vel print (" , ", " v=", vcurrent) else: # , : if (t+startingred)%(red+grn)<=red: t = int (((vel- vcurrent)/accel) + (scrit-saccel)/vel + (vel/decel)+ red-((t+startingred)%(red+grn)))### 5 vcurrent = 0 print (" , ") # - , , scrit : else: print ("scrit ", scrit) print ("vcurrent ", vcurrent) t = int (((vel- vcurrent)/accel) +(scrit-saccel)/vel + (vel - vnext)/((vel*(vel - vnext)/(dis-scrit))-((vel - vnext)*(vel - vnext)/(2*(dis-scrit))))) ### 6 vcurrent = vnext print (" , ", " v=", vcurrent) # , __ - , : else: print ("ERROR: v current > v next") print (t) r+=1 g+=1 d+=1 v+=1 gtime+=t print (gtime) Here you need a few clarifications.
I took the conditional dynamics of vehicle acceleration from 0 to 100 in 15 seconds, and set the braking twice as sharp. It seemed to me realistic, who does not agree - the code is in your hands, experiment with loaded wagons and Lamborghini Murcelago.
Yes, I neglected the fact that while the car slows down, the red light can turn green. It is unlikely, but this can be - equal slowdown to zero takes twice as long as traveling the same distance at a constant speed. So, we are talking about 3-5 seconds. For their sake, I didn’t bother with any more formulas, reassuring myself that this is a simulation of a car facing us at a traffic light. Kstaaaaati ...
Yes, I neglected traffic at all. Explain why. Purely mathematically, traffic will look like the offset of a traffic light point across several car bodies and, accordingly, a speed line shifted in phase. Just drag the image above a centimeter to the left with the mouse - a clear demonstration.
But the fact is that the reality is not like that. Machines will not start at the same time as subway cars, although theoretically they can do this without colliding. They start consistently, and this will affect our travel time as follows: we may not have time to drive a traffic light if there are quite a lot of them. Otherwise, this is only a phase shift and a decrease in the average speed at the site (as if stricter rules apply throughout the city). So, the situation is simulated by simply adding another traffic light cycle, like:
t = int (scrit/vel + (vel/decel) + red-((t+startingred)%(red+grn)) <b>+ (red+grn)</b>) Does this give us something? It is unlikely, since it is simply a summand, just another property of a traffic light, if you wish. The whole game with the passage of the route takes place during the movement on the segments. And here the dense traffic interfering with each other can be simulated by killing the acceleration or / and the allowed speed at the site.
But we are interested in how to limit the situation of speed limits, and not neighboring cars? So we will analyze this option.
I did not invent anything, but took the real city route. Let's just say, familiar to me earlier. I do not remember exactly all the phases of traffic lights, but I took it as the basis for the simulation, because there are both long and short, and speed-limited sections on it.
cry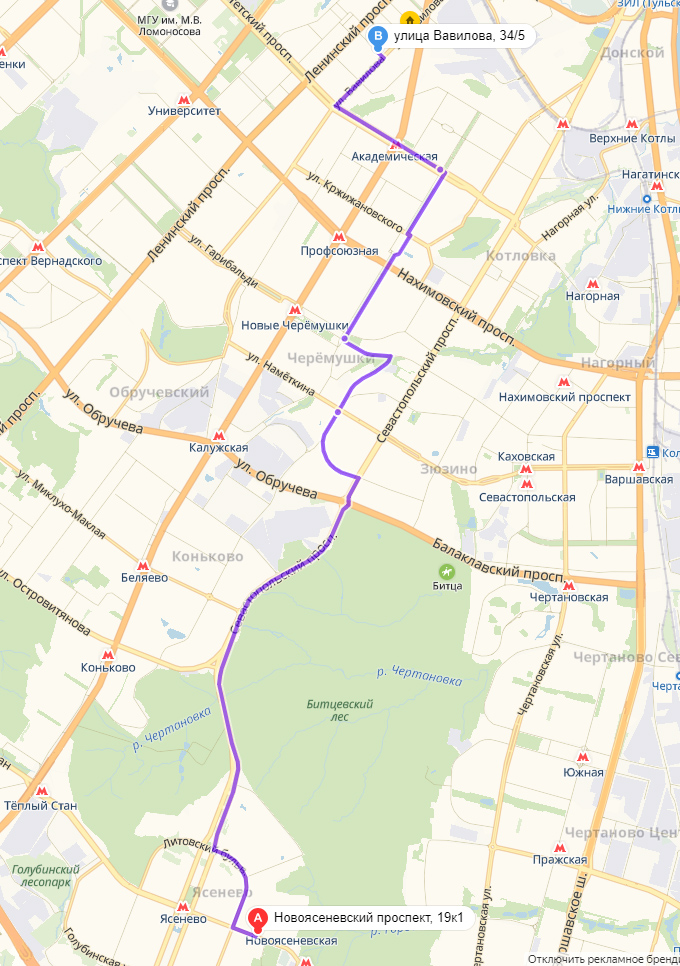

And I modified the code. Erased all kamenty and prints, added a more global cycle, to drive it, for example, 10,000 times:
cry
import random import math n=0 overalltime=0 while n<=10000: redlight = ("100", "10", "90", "20", "60", "20", "20", "20", "20", "60", "20", "20", "90", "90", "100", "60", "100", "80", "80", "60", "90", "60", "120", "60", "80", "60", "1", "1") greenlight = ("30", "120", "30", "120", "40", "120", "120", "120", "120", "40", "120", "120", "40", "15", "20", "20", "20", "20", "20", "40", "30", "20", "40", "40", "20", "40", "1", "1") distance = ("400", "400", "250", "250", "250", "450", "300", "650", "1000", "450", "500", "900", "450", "400", "1100", "900", "600", "1000", "450", "450", "400", "450", "200", "500", "350", "400", "500", "500") velocity = ("80", "80", "80", "80", "80", "80", "60", "80", "80", "80", "80", "80", "80", "80", "80", "80", "80", "60", "80", "80", "80", "80", "80", "60", "80", "80", "80", "40") r=0 g=0 d=0 v=0 vcurrent=float(0) t=0 gtime=0 accel=float(100/(3.6*15)) decel = float(accel*2) while r<=26: red=float(redlight[r]) grn=float(greenlight[g]) dis=float(distance[d]) vel=float(float(velocity[v])/3.6) vnext=float(float(velocity[v+1])/3.6) saccel = float((vcurrent*(vel-vcurrent)/accel) + (vel-vcurrent)*(vel-vcurrent)/(2*accel)) scrit = float(dis-(vel/decel) - (vel*vel)/(2*decel)) startingred = random.randint(0, (int(grn)-1)) if vcurrent == vel: if vnext>= vcurrent: t = int (dis/vel) if (t+startingred)%(red+grn)<=red: t = int (scrit/vel + (vel/decel) + red-((t+startingred)%(red+grn))) ### 2 vcurrent = 0 else: t = int (dis/vel)### 1 vcurrent = vel else: t = int ((scrit/vel) + (vcurrent - (vnext)/((vcurrent*(vcurrent - (vnext/(dis-scrit))- ((vcurrent - vnext)*(vcurrent - vnext)/(2*(dis-scrit)))))))) if (t+startingred)%(red+grn)<=red: t = int (scrit/vel + (vel/decel)+ red-((t+startingred)%(red+grn)))### 2 vcurrent = 0 else: t = int (scrit/vel + (vcurrent - vnext)/((vcurrent*(vcurrent - (vnext/(dis-scrit))- ((vcurrent - vnext)*(vcurrent - vnext)/(2*(dis-scrit)))))))### 3 vcurrent = float(vnext/3.6) elif vcurrent < vel: vcrit=math.sqrt(2*accel*scrit+vcurrent*vcurrent) if saccel >= scrit: if vnext >= vcrit: t = int(((vcrit-vcurrent)/ accel) + (dis-scrit)/vcrit) if (t+startingred)%(red+grn)<=red: t = int(((vcrit-vcurrent)/ accel) + ((dis-scrit)*2/vcrit) + red-((t+startingred)%(red+grn)))### 8 vcurrent = 0 else: t = int(((vcrit-vcurrent)/ accel) + (dis-scrit)/vcrit) ### 7 vcurrent = vcrit else: t = int(((vcrit-vcurrent)/ accel) + (vcrit - vnext)/((vcrit*(vcrit - vnext)/(dis-scrit))- ((vcrit - vnext)*(vcrit - vnext)/(2*(dis-scrit))))) if (t+startingred)%(red+grn)<=red: t = int(((vcrit-vcurrent)/ accel) + ((dis-scrit)*2/vcrit) + red-((t+startingred)%(red+grn)) ) ### 8 vcurrent = 0 else: t = int(((vcrit-vcurrent)/ accel) + (vcrit - vnext)/((vcrit*(vcrit - vnext)/(dis-scrit))- ((vcrit - vnext)*(vcrit - vnext)/(2*(dis-scrit))))) ### 9 vcurrent = vnext else: if vnext>= vel: t = int(((vel- vcurrent)/accel) + (dis-saccel)/vel) if (t+startingred)%(red+grn)<=red: t = int (((vel- vcurrent)/accel) + (scrit-saccel)/vel + (vel/decel)+ red-((t+startingred)%(red+grn)))### 5 vcurrent = 0 else: t = int (((vel- vcurrent)/accel) + (dis-saccel)/vel)### 4 vcurrent = vel else: if (t+startingred)%(red+grn)<=red: t = int (((vel- vcurrent)/accel) + (scrit-saccel)/vel + (vel/decel)+ red-((t+startingred)%(red+grn)))### 5 vcurrent = 0 else: t = int (((vel- vcurrent)/accel) +(scrit-saccel)/vel + (vel - vnext)/((vel*(vel - vnext)/(dis-scrit))-((vel - vnext)*(vel - vnext)/(2*(dis-scrit))))) ### 6 vcurrent = vnext else: print ("ERROR: v current > v next") #print (t) r+=1 g+=1 d+=1 v+=1 gtime+=t dev=(1476-gtime)*(1476-gtime) #print (gtime) n+=1 dev+=dev overalltime+=gtime print ("mean= ", overalltime/n) print ("deviation= ", math.sqrt(dev/n)) The presented option displays the "normal driving" - with a maximum speeding, which is punished only by verbal warning.
But now it will be interesting to compare the following options with the help of a simulation based on this route: introducing a non-penalized interval of 10 km / h, super-obedient driving precisely according to restrictions, pedalized by urbanists with a maximum city speed of 50 km / h.
Results of 10,000 simulations, raw data:
(limit, km / h; route time, s; standard deviation):
90 1466,6 0,5 80 1475,6 0,4 70 1479,7 0,9 60 1593,7 0,8 50 1701,3 0,5 40 1869,8 0,6 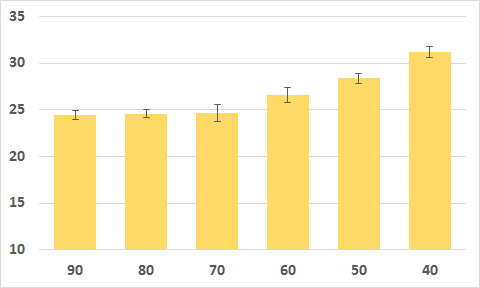
The chart shows the minutes of the journey depending on the global speed limit. Yes, I know that the Y axis is not from scratch, but it is more obvious.
The results seemed a little unexpected. Firstly, the planned reduction of the non-penalized threshold on this route really does not lead to a significant increase in travel time . And starting just somewhere from 70 km / h, an increase in speed gives almost nothing. Secondly, the reduction of the allowed speed will significantly increase the time, by 8% even by relatively completely law-abiding citizens and by 13% from tacitly exploited speeds of “oral warning”. That is, the statement that the decrease in the allowed speed does not affect the average is strictly speaking incorrect . Again, within the framework of this model, it is impossible to show whether a slowdown by 10% will “stack” in conditions of heavy traffic and aggravate the traffic situation.
Please write comments on the model (again, constructive), but if you put your routes into the model and bring the result in the comments, it will be great in general.
Source: https://habr.com/ru/post/442602/
All Articles