Intuitive RL (Reinforcement Learning): An Introduction to Advantage-Actor-Critic (A2C)

This is a free translation of the article by Rudy Gilman and Katherine Wang Intuitive RL: Intro to Advantage-Actor-Critic (A2C) .

Reinforcement Training Specialists (RL) have produced many excellent tutorials. Most, however, describe RL in terms of mathematical equations and abstract diagrams. We like to think about the subject from a different point of view. RL itself is inspired by how animals learn, so why not translate the underlying RL mechanism back into the natural phenomena that it is meant to imitate? People learn best through stories.

This is a story about the Actor Advantage Critic (A2C) model. The “Subject Critic” model is a popular form of the Policy Gradient model, which itself is a traditional RL algorithm. If you understand A2C, you understand deep RL.

After you gain an intuitive understanding of A2C, check:

• Our simple implementation of the A2C code (for training) or our industrial version of PyTorch , based on the OpenAI TensorFlow Baselines model;
• Introduction to RL by Barto & Sutton , David Silver’s canonical course , review by Yusi Lee and the Denny Brits repository on GitHub for deep immersion in RL;
• Amazing fast.ai course for intuitive and practical coverage of deep learning in general, implemented in PyTorch;
• Tutorials by Arthur Giuliani on RL, implemented in TensorFlow.

@Embermarke Illustrations

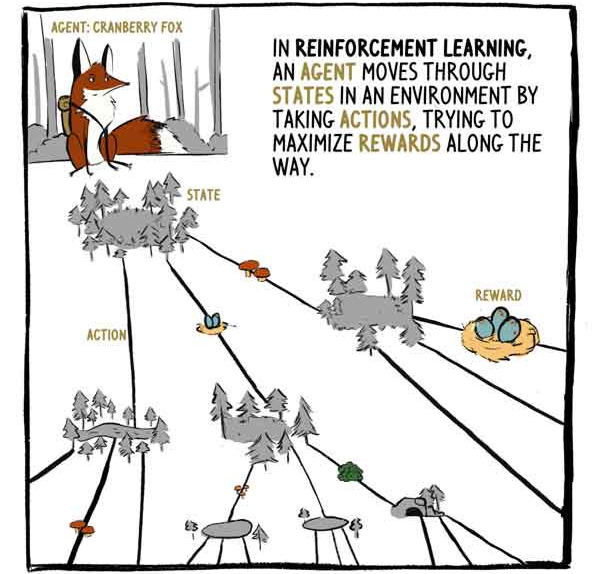
In RL, the agent (agent) - Fox Klukovka, - moves through the states in the environment by performing actions (actions), trying to maximize rewards during the journey.

A2C accepts status inputs — sensory inputs in the Klucke case — and generates two outputs:
1) Estimation of how much remuneration will be received, starting from the moment of the current status, except for the current (already existing) remuneration.
2) Recommend what action to take (policy).

"Critic": wow, what a wonderful valley! It will be a fruitful day for foraging! I bet today, before sunset, I will collect 20 points.
"Subject": these flowers look beautiful, I feel a craving for "A."

Deep RL models are input-output display machines, like any other classification or regression models. Instead of categorizing images or text, deep RL models lead states to actions and / or states to state values. A2C does both.

This state-action-reward set constitutes one observation. She will write this line of data in her journal, but she is not going to think about it yet. She will fill it when she stops to think.

Some authors associate reward 1 with a time step of 1, others associate it with step 2, but all mean the same concept: reward is related to the state, and the action immediately precedes it.

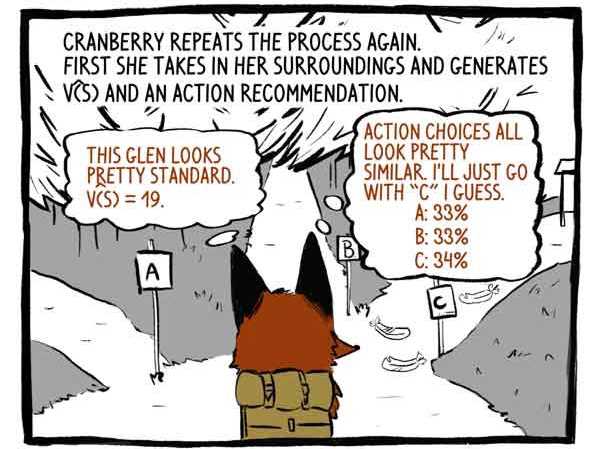
Klyukovka repeats the process again. At first, she perceives her environment and produces a function V (S) and a recommendation for action.
')
"Critic": This valley looks pretty standard. V (s) = 19.
"Subject": Action options look very similar. I think I'll just go along track "C".

Further, it acts.

Receives a reward of +20! And records the observation.

She repeats the process again.

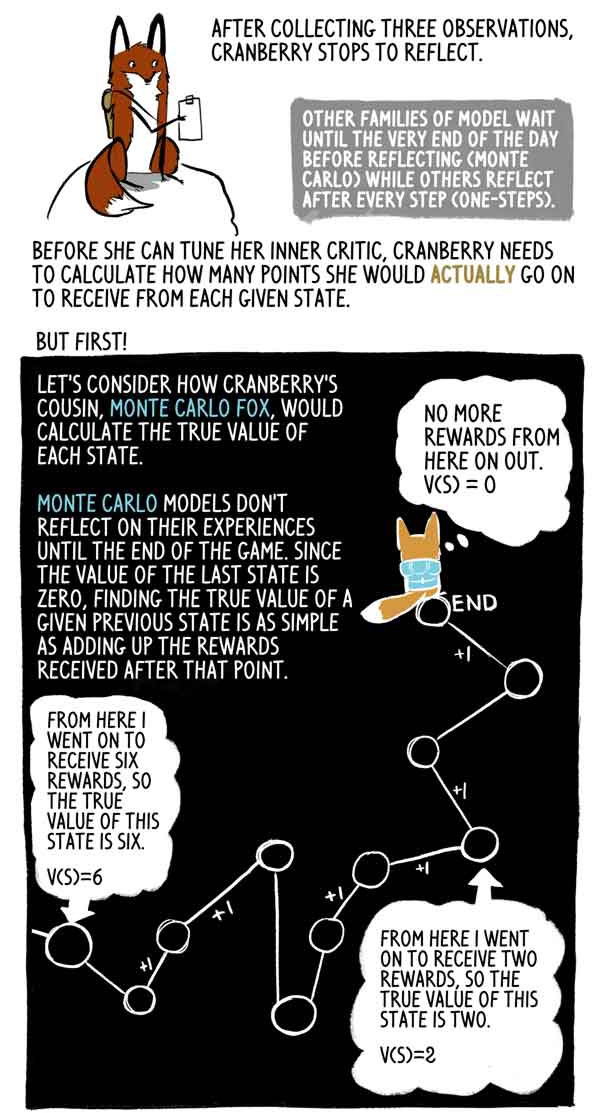
After collecting three observations, Klyukovka stops thinking.

Other model families are waiting for the moment of reflection until the very end of the day (Monte Carlo), while others are thinking after each step (one-steps).
Before she can set up her inner critic, Klukovka needs to calculate how many points she actually gets in each given state.

But first!
Let's take a look at how Klukowka's cousin, Lys Monte Carlo, calculates the true value of each state.

Monte Carlo models do not reflect their experience until the end of the game, and since the value of the last state is zero, it is very simple to find the true value of this previous state, as the sum of the rewards received after this point.

In fact, this is just a high dispersion V (S) sample. The agent could easily follow a different path from the same state, thereby obtaining a different aggregate reward.

But Klukovka goes, stops and reflects many times, until the day comes to an end. She wants to know how many points she really gets from each state until the end of the game, because there are several hours left until the end of the game.

That's where she does something really clever - Fox Klukovka assesses how many points she gets for the last state in this set. Fortunately, she has the correct assessment of the state - her critic.
With this estimate, Klukovka can calculate the “correct” values ​​of the preceding states exactly as a Monte Carlo one does.

Lees Monte Carlo evaluates target tags by deploying a trajectory and adding rewards ahead of each state. A2C cuts this trajectory and replaces it with an assessment of its critic. This initial load reduces the variance of the estimate and allows the A2C to operate continuously, albeit by introducing a small offset.

Rewards are often reduced to reflect the fact that rewards are now better than in the future. For simplicity, Cranberry does not lower its rewards.

Now Klukovka can go through each data line and compare its estimates of state values ​​with its actual values. She uses the difference between these numbers to hone prediction skills. Every three steps throughout the day, Klukovka gathers valuable experience to think about.

“I didn’t rate states 1 and 2 badly. Aha The next time I see feathers like these, I will increase V (S).

It may seem crazy that Klukovka is able to use his V (S) estimate as a basis to compare it with other forecasts. But animals (including us) do it all the time! If you feel that things are going well, you do not need to retrain the actions that led you to this state.

By trimming our calculated outputs and replacing them with the initial load estimate, we replaced the large Monte Carlo variance with a small offset. RL models usually suffer from high dispersion (representing all possible trajectories), and such a replacement is usually worth it.

Klyukovka repeats this process all day, collecting three observations of state-action-reward and reflecting on them.

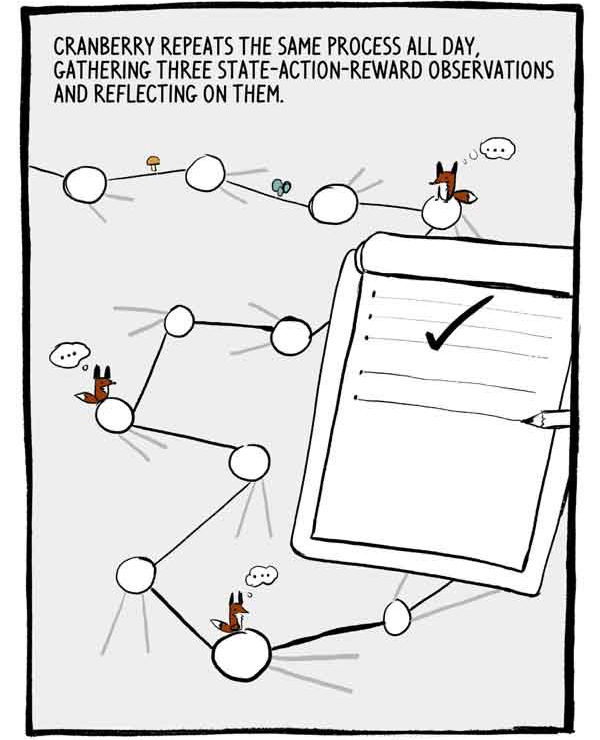
Each set of three observations is a small, autocorrelated series of labeled training data. To reduce this autocorrelation, many A2C train many agents in parallel, putting their experience together before sending it into a common neural network.

The day is finally coming to an end. There are only two steps left.
As we said earlier, recommendations for Kluk’s actions are expressed in percent certainty about its capabilities. Instead of simply choosing the most reliable choice, Klukovka selects from this distribution of actions. This ensures that she does not always agree to safe, but potentially mediocre actions.

I could regret it, but ... Sometimes, exploring unknown things, you can come to exciting new discoveries ...

To further promote research, a value called entropy is subtracted from the loss function. Entropy means "span" of the distribution of actions.
- It looks like the game has paid off!

Or not?

Sometimes an agent is in a state where all actions lead to negative outcomes. A2C, however, does an excellent job with bad situations.

When the sun went down, Klyukovka reflected on the latest set of solutions.

We talked about how Klyukovka sets up his inner critic. But how does she adjust her inner "subject"? How does she learn to make such sophisticated choices?

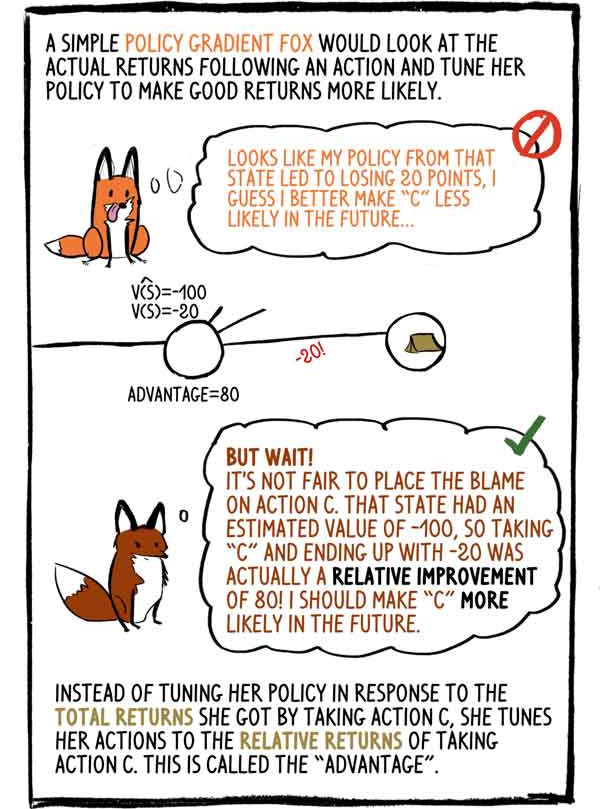
The simple-minded fox Gradient-Policy would look at the actual incomes after the action and set up their policies to make good returns more likely: - It seems that my policy in this state led to a loss of 20 points, I think that in the future it is better to do the less likely.

- But wait! It is not fair to put the blame on the action "C". This condition had an estimated value of -100, so the choice of “C” and its ending from -20 was in fact a relative improvement of 80! I must make the "C" more likely in the future.

Instead of setting up its policy in response to the total income it received by choosing action C, it adjusts its action to relative income from action C. This is called an “advantage”.

What we have called an advantage is simply a mistake. As an advantage, Klukovka uses it to make actions that were surprisingly good, more likely. As an error, it uses the same magnitude to push its internal critic to improve the assessment of the value of the state.

Subject takes advantage of:
“Wow, that worked better than I thought, acting C must have been a good idea."
The critic uses the error:
“But why was I surprised? I probably should not have rated this state so negatively. ”

Now we can show how total losses are calculated - we minimize this function to improve our model.
“Total loss = loss of action + loss of value — entropy”

Note that to calculate the gradients of three qualitatively different types, we take the values ​​“through one”. This is effective, but can make convergence more difficult.

Like all animals, as he grows up, Klukovka will sharpen his ability to predict the values ​​of states, gain greater confidence in his actions and be less likely to be surprised at the rewards.

RL agents, such as Klukovka, not only generate all the necessary data, simply interacting with the environment, but also evaluate target labels themselves. All so, the RL models update the previous estimates to better match the new and improved estimates.

As Dr. David Silver, head of the RL group at Google Deepmind, says: AI = DL + RL. When an agent like Klukovka can set up his own intelligence, the possibilities are endless ...