Some tasks of school mathematics. Part II
Part I. Fractions
Part II. Modules
This article discusses the method of estimating the range of accepted values and the relationship of this method with the tasks containing the module.
When solving some problems, it is necessary to consider the range within which the desired value may be.
')
Consider the method of estimation when solving inequalities.
Suppose that the price for a single item can vary from 5 to 10 RUB. To give a top estimate means to determine the maximum value that the desired value can take. For two units of goods, the price for which does not exceed 10, the upper rating will be 10 + 10 = 20 .
Consider the task from the taskbook of the profile orientation of M.I. Bashmakova
37. Known estimates for variables and
Give top estimates for the following expressions:
one.
2
five.
6
eight.
9.
In general, the analysis of infinitely small quantities uses an evaluation criterion. The concept of a module as a neighborhood lies in the definition of the limit itself.
Consider an example from the Course of Differential and Integral Calculus 363 (6)
Making the addition of all the inequalities of this system, we get
This is proof that this series diverges.
With a harmonic series, such reception does not work, because -th partial sum of the harmonic series
Let's return to the task
38. Calculate the amount ("Tasks for children from 5 to 15 years")
(with an error of not more than 1% of the answer)
Estimate from above sum of series gives the number 1.
Drop the first addend
Will get
0.41666666666666663
0.49019607843137253
0.4990019960079833
0.4999000199960005
0.49999000019998724
0.4999990000019941
You can check it at ideone.com here.
Drop the first two terms.
We get 0.33333233333632745
Partial sums of a series are bounded above.
Throw away the initial components of the harmonic series.
Prove (using the lower bound) that
Calculate the partial amounts that are obtained by dropping terms.
We get:
0.5833333333333334
0.6345238095238095
0.6628718503718504
We write a program that calculates the sum of the harmonic series from before where at
We get:
0.5833333333333333
0.6345238095238095
0.6628718503718504
0.6777662022075267
You can check in the online ide link
For range we get 0.693147 ...
Check out the Wolfram Cloud here .
This recursive algorithm causes a fast stack overflow.
This article has an example of factorial calculation using an iterative algorithm. We modify this iterative algorithm so that it calculates the partial sum Hn within certain bounds; let's call these boundaries a and b
The bottom is the number , the upper bound is the number
We write a function that calculates the power of two
We will substitute (+ 1 (power_of_two k)) as the lower border, and use the function (* 2 (power_of_two k)) or its equivalent function (power_of_two (+ 1 k)) as the top border
Rewrite the function Hn
Now you can calculate Hn for large values .
We write in C language a program that measures the time needed to calculate Hn . We will use the clock () function from the standard library <time.h>
Article about measurement of processor time is on Habré here .
Let's return to the modules.
In integral calculus, the module is used in the formula
On Habré there was an article The most natural logarithm in which this integral is considered and based on its calculation of the number .
The presence of the module in the formula further substantiated in the "Course of differential and integral calculus"
This integral is used to calculate the potential difference between the plates of a cylindrical capacitor.
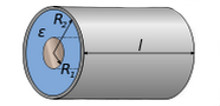
"Electricity and Magnetism":
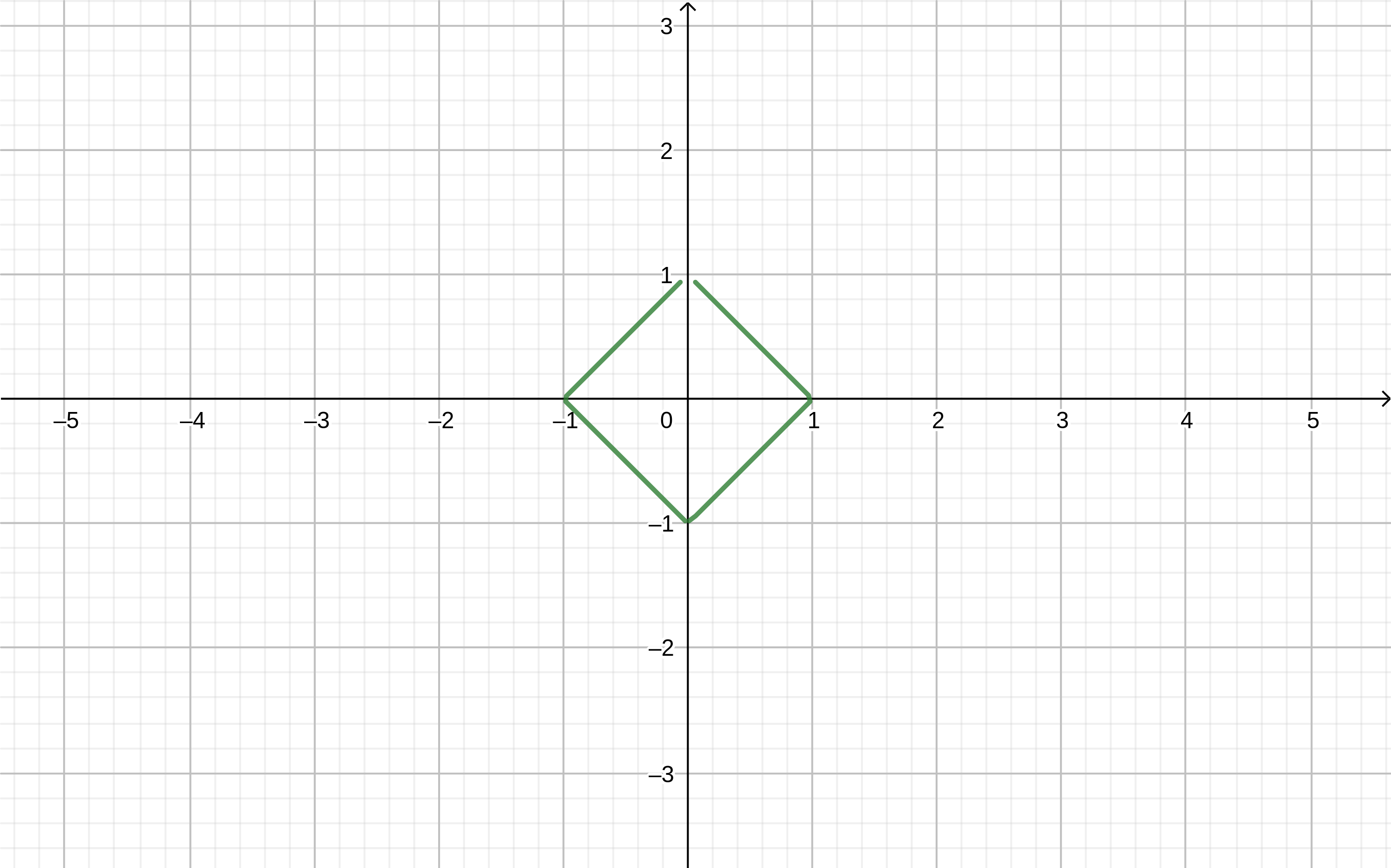
With the help of modules you can draw various shapes.
If the program geogebra write the formula will get
You can draw more complex shapes. For example, let's draw a “butterfly” in the WolframAlpha cloud.
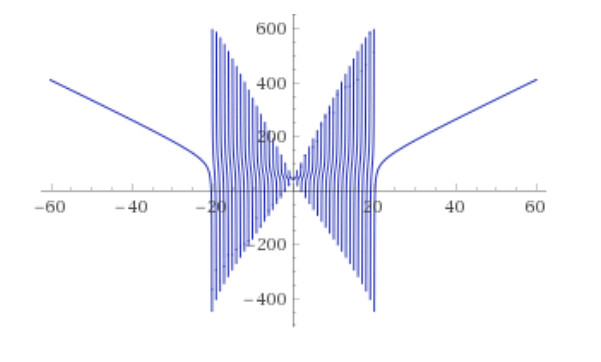
Plot [Sum [abs (x) / (n-abs (x)) + abs (x + n) / (n) + abs (xn) / (n), {n, 1.20}], {x, -60,60}]
In this expression lies in the range of before , lies in the range of before .
Link to the picture.
"The task book of the profile orientation" M.I. Bashmakov
The course of general physics: in 3 tons. T. 2. “Electricity and magnetism” I.V. Saveliev
Part II. Modules
This article discusses the method of estimating the range of accepted values and the relationship of this method with the tasks containing the module.
When solving some problems, it is necessary to consider the range within which the desired value may be.
')
Consider the method of estimation when solving inequalities.
Suppose that the price for a single item can vary from 5 to 10 RUB. To give a top estimate means to determine the maximum value that the desired value can take. For two units of goods, the price for which does not exceed 10, the upper rating will be 10 + 10 = 20 .
Consider the task from the taskbook of the profile orientation of M.I. Bashmakova
37. Known estimates for variables and
Give top estimates for the following expressions:
one.
2
The instruction to the decision of problems 5 and 6
To evaluate fractional expressions, you must use the following property of numerical inequalities:
- If a and both numbers are positive, then
five.
6
eight.
9.
Answers
one.
five.
9.
five.
9.
In general, the analysis of infinitely small quantities uses an evaluation criterion. The concept of a module as a neighborhood lies in the definition of the limit itself.
Consider an example from the Course of Differential and Integral Calculus 363 (6)
It is easy to establish the divergence of the seriesIn order to prove that really more , you need to evaluate the bottom of this expression. We get a system of inequalities
In fact, since its members decrease, the nth partial sum
and grows to infinity along with .
\ left \ {\! \ begin {aligned} & \ frac {1} {\ sqrt {n-1}}> \ frac {1} {\ sqrt {n}} \\ & \ frac {1} {\ sqrt {n-2}}> \ frac {1} {\ sqrt {n}} \\ & \ frac {1} {\ sqrt {n-3}}> \ frac {1} {\ sqrt {n}} \\ & ... \ end {aligned} \ right.
Making the addition of all the inequalities of this system, we get
This is proof that this series diverges.
With a harmonic series, such reception does not work, because -th partial sum of the harmonic series
Let's return to the task
38. Calculate the amount ("Tasks for children from 5 to 15 years")
\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1 {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}
(with an error of not more than 1% of the answer)
Estimate from above sum of series gives the number 1.
Drop the first addend
(define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 1.0 )(+ n 2.0))) (series_sum_1(- n 1.0))) ) ) ) (writeln (series_sum_1 10)) (writeln (series_sum_1 100)) (writeln (series_sum_1 1000)) (writeln (series_sum_1 10000)) (writeln (series_sum_1 100000)) (writeln (series_sum_1 1000000)) Will get
0.41666666666666663
0.49019607843137253
0.4990019960079833
0.4999000199960005
0.49999000019998724
0.4999990000019941
You can check it at ideone.com here.
The same algorithm in Python
Link to ideone.com
def series_sum(n): if n==0: return 0 else: return 1.0/((n+1.0)*(n+2.0))+series_sum(n-1.0) print(series_sum(10)) print(series_sum(100)) Link to ideone.com
Drop the first two terms.
(define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 2.0) (+ n 3.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 1000000) We get 0.33333233333632745
Partial sums of a series are bounded above.
A positive row always has an amount; this sum will be finite (and, therefore, the row will converge) if the partial sums of the row are bounded above, and infinite (and the row divergent) otherwise.
Calculate the sum of the harmonic series with increasing n
We get:
2.9289682539682538
5.187377517639621
7.485470860550343
9.787606036044348
12.090146129863335
14.392726722864989
#lang racket (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 n) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 10) (series_sum_1 100) (series_sum_1 1000) (series_sum_1 10000) (series_sum_1 100000) (series_sum_1 1000000) We get:
2.9289682539682538
5.187377517639621
7.485470860550343
9.787606036044348
12.090146129863335
14.392726722864989
Throw away the initial components of the harmonic series.
Prove (using the lower bound) that
If, discarding the first two members, the remaining members of the harmonic series are divided into groups by members in each
then each of these amounts separately will be more .
... We see that partial sums cannot be bounded above: the series has an infinite sum.
Calculate the partial amounts that are obtained by dropping terms.
#lang racket (* 1.0 (+ 1/3 1/4)) (* 1.0 (+ 1/5 1/6 1/7 1/8)) (* 1.0 (+ 1/9 1/10 1/11 1/12 1/13 1/14 1/15 1/16)) We get:
0.5833333333333334
0.6345238095238095
0.6628718503718504
We write a program that calculates the sum of the harmonic series from before where at
#lang racket (define (Hn n ) (define half_arg (/ n 2.0)) (define (series_sum n) (if (= n half_arg ) 0 (+ (/ 1.0 n) (series_sum(- n 1)) ) ) ) (series_sum n) ) (Hn 4) (Hn 8) (Hn 16) (Hn 32) We get:
0.5833333333333333
0.6345238095238095
0.6628718503718504
0.6777662022075267
You can check in the online ide link
For range we get 0.693147 ...
Check out the Wolfram Cloud here .
This recursive algorithm causes a fast stack overflow.
This article has an example of factorial calculation using an iterative algorithm. We modify this iterative algorithm so that it calculates the partial sum Hn within certain bounds; let's call these boundaries a and b
(define (Hn ab) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a)) The bottom is the number , the upper bound is the number
We write a function that calculates the power of two
(define (power_of_two k) (define (iteration product counter) (if (> counter k) product (iteration (* product 2) (+ counter 1)))) (iteration 1 1)) We will substitute (+ 1 (power_of_two k)) as the lower border, and use the function (* 2 (power_of_two k)) or its equivalent function (power_of_two (+ 1 k)) as the top border
Rewrite the function Hn
(define (Hn k) (define a (+ 1 (power_of_two k)) ) (define b (* 2 (power_of_two k)) ) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a )) Now you can calculate Hn for large values .
We write in C language a program that measures the time needed to calculate Hn . We will use the clock () function from the standard library <time.h>
Article about measurement of processor time is on Habré here .
#include <math.h> #include <stdio.h> #include <time.h> int main(int argc, char **argv) { double count; // 1+2^30 -> 2^31 for(unsigned long long int i=1073741825 ;i<=2147483648 ;i++) { count=count+1.0/i; } printf("Hn = %.12f ", count); double seconds = clock() / (double) CLOCKS_PER_SEC; printf(" %f \n", seconds); return 0; } Let's return to the modules.
In integral calculus, the module is used in the formula
On Habré there was an article The most natural logarithm in which this integral is considered and based on its calculation of the number .
The presence of the module in the formula further substantiated in the "Course of differential and integral calculus"
If a… then it’s easy to make sure that
Physical integral application
This integral is used to calculate the potential difference between the plates of a cylindrical capacitor.

"Electricity and Magnetism":
The potential difference between the plates we find by integrating:The module sign under the sign of the natural logarithm is not used here. , because and strictly positive and this form of writing is redundant.
( and - the radii of the inner and outer plates).
"Modular" drawing
With the help of modules you can draw various shapes.
If the program geogebra write the formula will get

You can draw more complex shapes. For example, let's draw a “butterfly” in the WolframAlpha cloud.

Plot [Sum [abs (x) / (n-abs (x)) + abs (x + n) / (n) + abs (xn) / (n), {n, 1.20}], {x, -60,60}]
In this expression lies in the range of before , lies in the range of before .
Link to the picture.
Books:
"The task book of the profile orientation" M.I. Bashmakov
The course of general physics: in 3 tons. T. 2. “Electricity and magnetism” I.V. Saveliev
Source: https://habr.com/ru/post/442330/
All Articles