Life on particles
Hello! Today I will talk about my experiments with particle systems. The main goal was to find simple rules that would generate interesting behavior.
A classic example of a system with simple rules and complex behavior is cellular automata, I was guided exactly by them, trying to choose rules. Of course, for cellular automata, the rules will in most cases be simpler. But particles can be more beautiful!
Under the cat a lot of megabytes gif.
')
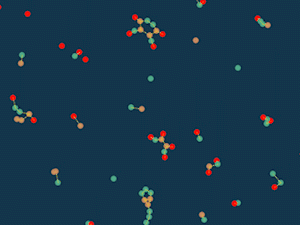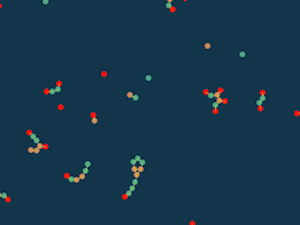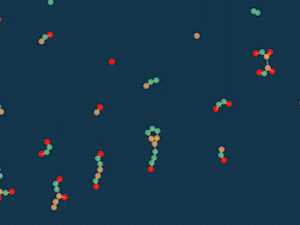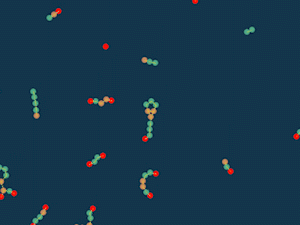
At first I followed in the footsteps of the “life” game: each particle has a “overpopulation” counter, which is equal to the sum of the inverse squares of distances to other particles. If this counter is less than a certain limit, that is, there are few neighbors, then the particle is attracted to other particles, and if there are many neighbors, it is repelled. If the particles intersect, then they repel in any case, so as not to pass through each other.
Randomly scatter particles across the field and see what happens.

Interestingly, something turns out similar to the cells and looks quite lively. You can, for example, add more types of particles. Let different particles increase the number of neighbors in different ways, and some even be able to reduce it.

Now our “cells” have become multi-layered.
The disadvantage of such rules is that they get rather chaotic, not very stable structures.
Therefore, we go further.
Change the rules of the game. We will no longer be considered neighbors. Let the particles be simply attracted or repelled depending on their types. If all the particles are of the same type, then there are only 2 options: they either all repel, or all attract.

If there are more types of particles, then you can combine which ones will be attracted to, and which ones will repel.
Any such rule can be represented as a matrix N * N, where N is the number of types of particles, and in each cell either attraction or repulsion. The attraction is denoted by 0, and the repulsion - by 1. Then any matrix corresponds to a certain number, for example, the matrix would mean 0101, that is, 5 (the last digit in binary form is the first in the matrix). The number of different matrices for the rules is equal to . For example, for two types of particles, there are 16 rules.

It may seem that rule 3 is the same, as rule 7, but if you translate them into matrices, you get and , which means that in rule 7 only beige attracts each other. While in rule 3, beige is also attracted to red. But because of the low density of red, this has a subtle effect. In reality, the same rules can be called, for example, 3 and 12, since the whole behavior of the particles is identical, only the colors have changed places. If we leave only the rules with a unique behavior, then out of 16 rules we will have 10. For three types of particles, out of 512 possible combinations, 104 remain unique, and for four - 3044 out of 65536 This results in a sequence of 2, 10, 104, 3044 .
But back to our ten rules.

Rule 9, which is a matrix, catches the eye where the same repel, and different attract. Randomly scattered particles quickly form a “thread” and freeze on it.
Rules 1 and 15 also freeze: they are equivalent to two unique rules for one type of particles (the previous animated gif). Usually freeze all the rules, the matrices of which are symmetrical. There are also rules 2, 3, 5, and 11 with asymmetric matrices. This means that one type of particles is attracted to the second, and the second is repelled from the first. Begin "catch up".

Rule 3 is too stable, in it “catch-up” stops at some moment, and if it renews, it is rare and not for long. Rule 11 is too chaotic. Remain 2 and 5.
You can somehow combine them to make it even more interesting. I picked up rule 105 for three colors, that is, the matrix , and this is the behavior:

It all looks alive, but unstable. But what about certain repetitive "living" creatures? How to search for oscillators and gliders? We must change the rules again!
We will not change the rules much. Instead, add a new feature. Now the particles at a short distance will form a connection. If particles are bound, they are constantly attracted to each other. This attraction does not weaken with distance. But, if the distance is above a certain threshold, then the connection is broken.
I tried different variants with three colors and stopped at where red can form only one bond, beige three, and blue blue, that is, you can designate maximum connections in the form .
At the same time, reds cannot bind with other reds, beige and blue can have no more than two bonds with particles of their own color and no more than one with particles of each other color. This is all in the form of a matrix:

I played with different rules of attracting / pushing away, and I liked it , that is, the red ones are attracted to the blue ones, and in all other cases all repel each other.

It seems as if these creatures are swimming in liquid or flapping their wings.


A pair of oscillators and a pair of gliders.
Fixed figures are easy to get: you just need not use red and blue together, as in these rules it is the only combination with attraction.


But sometimes the movement occurs with such colors. Some figures begin to unwind, pushing away from others, get "gears".

In the future, it would be interesting to compare the figures obtained, to collect statistics on the frequency of their appearance.
You can also use these rules as a basis for creating more complex creatures with food, reproduction, evolution.
You can build logic from this, build a calculator, the processor is better not to.
Implementation on JS from v1vendi
Java code
Cosmic
Particle Life
Clusters
A classic example of a system with simple rules and complex behavior is cellular automata, I was guided exactly by them, trying to choose rules. Of course, for cellular automata, the rules will in most cases be simpler. But particles can be more beautiful!
Under the cat a lot of megabytes gif.
')

Cell soup
At first I followed in the footsteps of the “life” game: each particle has a “overpopulation” counter, which is equal to the sum of the inverse squares of distances to other particles. If this counter is less than a certain limit, that is, there are few neighbors, then the particle is attracted to other particles, and if there are many neighbors, it is repelled. If the particles intersect, then they repel in any case, so as not to pass through each other.
Randomly scatter particles across the field and see what happens.

Interestingly, something turns out similar to the cells and looks quite lively. You can, for example, add more types of particles. Let different particles increase the number of neighbors in different ways, and some even be able to reduce it.

Now our “cells” have become multi-layered.
The disadvantage of such rules is that they get rather chaotic, not very stable structures.
Therefore, we go further.
Catch up game
Change the rules of the game. We will no longer be considered neighbors. Let the particles be simply attracted or repelled depending on their types. If all the particles are of the same type, then there are only 2 options: they either all repel, or all attract.

If there are more types of particles, then you can combine which ones will be attracted to, and which ones will repel.
Hidden text
In addition to attraction / repulsion, one could add other options, for example, so that the particles did not react to each other, or add coefficients to the force of impact, but I could not find any interesting behavior in this.
Any such rule can be represented as a matrix N * N, where N is the number of types of particles, and in each cell either attraction or repulsion. The attraction is denoted by 0, and the repulsion - by 1. Then any matrix corresponds to a certain number, for example, the matrix would mean 0101, that is, 5 (the last digit in binary form is the first in the matrix). The number of different matrices for the rules is equal to . For example, for two types of particles, there are 16 rules.

It may seem that rule 3 is the same, as rule 7, but if you translate them into matrices, you get and , which means that in rule 7 only beige attracts each other. While in rule 3, beige is also attracted to red. But because of the low density of red, this has a subtle effect. In reality, the same rules can be called, for example, 3 and 12, since the whole behavior of the particles is identical, only the colors have changed places. If we leave only the rules with a unique behavior, then out of 16 rules we will have 10. For three types of particles, out of 512 possible combinations, 104 remain unique, and for four - 3044 out of 65536 This results in a sequence of 2, 10, 104, 3044 .
But back to our ten rules.

Rule 9, which is a matrix, catches the eye where the same repel, and different attract. Randomly scattered particles quickly form a “thread” and freeze on it.
Rules 1 and 15 also freeze: they are equivalent to two unique rules for one type of particles (the previous animated gif). Usually freeze all the rules, the matrices of which are symmetrical. There are also rules 2, 3, 5, and 11 with asymmetric matrices. This means that one type of particles is attracted to the second, and the second is repelled from the first. Begin "catch up".

Rule 3 is too stable, in it “catch-up” stops at some moment, and if it renews, it is rare and not for long. Rule 11 is too chaotic. Remain 2 and 5.
You can somehow combine them to make it even more interesting. I picked up rule 105 for three colors, that is, the matrix , and this is the behavior:

It all looks alive, but unstable. But what about certain repetitive "living" creatures? How to search for oscillators and gliders? We must change the rules again!
Floating life
We will not change the rules much. Instead, add a new feature. Now the particles at a short distance will form a connection. If particles are bound, they are constantly attracted to each other. This attraction does not weaken with distance. But, if the distance is above a certain threshold, then the connection is broken.
I tried different variants with three colors and stopped at where red can form only one bond, beige three, and blue blue, that is, you can designate maximum connections in the form .
At the same time, reds cannot bind with other reds, beige and blue can have no more than two bonds with particles of their own color and no more than one with particles of each other color. This is all in the form of a matrix:

I played with different rules of attracting / pushing away, and I liked it , that is, the red ones are attracted to the blue ones, and in all other cases all repel each other.

It seems as if these creatures are swimming in liquid or flapping their wings.


A pair of oscillators and a pair of gliders.
Fixed figures are easy to get: you just need not use red and blue together, as in these rules it is the only combination with attraction.


But sometimes the movement occurs with such colors. Some figures begin to unwind, pushing away from others, get "gears".

Conclusion
In the future, it would be interesting to compare the figures obtained, to collect statistics on the frequency of their appearance.
You can also use these rules as a basis for creating more complex creatures with food, reproduction, evolution.
To play
Implementation on JS from v1vendi
Sources
Java code
Similar cool stuff
Cosmic
Particle Life
Clusters
Source: https://habr.com/ru/post/442128/
All Articles