Summing up the online contest on the game Blotto
A few days ago I held an online contest on the game .
1199 people took part in the online contest, and more than 5000 solutions were gathered, among which 61 solutions were attempts to bypass the system by finding vulnerabilities. This is very cool, thanks to everyone who participated.
This game is a type of " games of Colonel Blotto ". Two players take part in it. Each has the same number of resources that must be placed on the NxM field. The winner is the one who takes more cells (i.e., the number of your resources on it is greater than that of your opponent). This is the condition for our task.
When I launched this experiment, I still did not know that this game has no perfect solution, but thanks to the comments I was able to better understand this topic.
Let's start with the winners of this game.
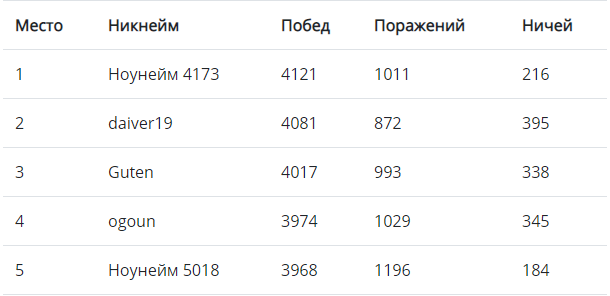
The best solution scored 4121 wins - a very good result. But what would happen if solutions from only TOP-100 participated in the game?
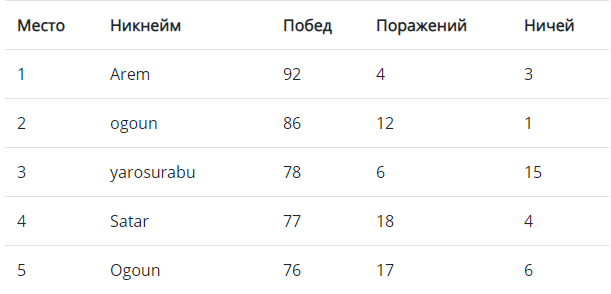
Surprisingly, it did not even enter the top5 (in 8th place), and the 1st place here was taken by the decision from 68th place.
This just shows that there is no better solution. The remaining results can be viewed at game.pavlukhinlab.com
But what else can you learn?
The largest numbers of players were placed in the center, on average, all the players filled the first row with larger numbers, while the best results placed greater emphasis on the bottom row.


average values for all games (left) and TOP-100 (right)
Well, and more examples of the best strategies:
The best strategies chose 5 main cells, the remaining cells were filled with small values. Which is logical, because for victory, it is enough to take 5 cells.
And now some graphs.
Probability distributions of numbers:
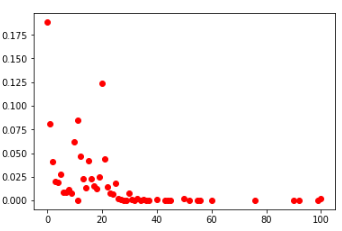
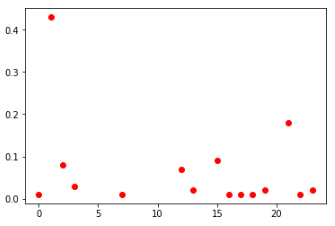
second cells among all players (left) and TOP-100 (right)
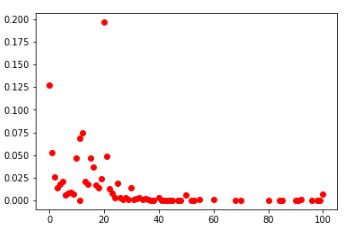
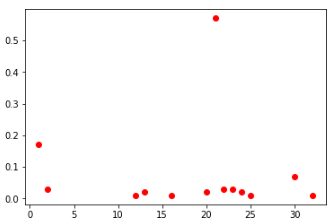
central cells among all and TOP-100
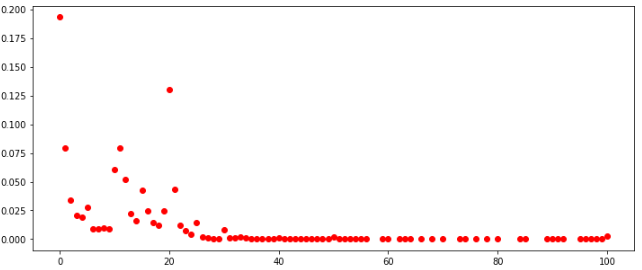
number distribution for all games
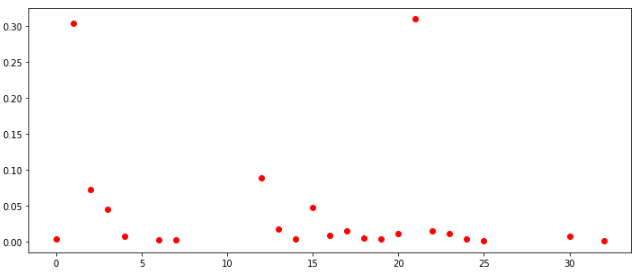
distribution of numbers on the TOP-100
If you look at the distribution of all cells among all players, then they look generally similar. You can also conclude that in these conditions it makes no sense to fill the cells with values greater than 30.
At this point, the study comes to an end - that's all I could extract from this data. Perhaps some of you will be able to offer something else that can be checked - I am waiting for you in the comments. Impersonal games look for the link .
Py.Sy. In the previous post, I talked about the neuron, which was trained to play this game. Unfortunately, none of this has happened yet. Two neurons decided that the best strategy is to throw zeros at the output and enjoy a draw. But maybe I will understand this topic and make a separate post dedicated to the mistakes that I made when creating a neuron, and, perhaps, success.
1199 people took part in the online contest, and more than 5000 solutions were gathered, among which 61 solutions were attempts to bypass the system by finding vulnerabilities. This is very cool, thanks to everyone who participated.
This game is a type of " games of Colonel Blotto ". Two players take part in it. Each has the same number of resources that must be placed on the NxM field. The winner is the one who takes more cells (i.e., the number of your resources on it is greater than that of your opponent). This is the condition for our task.
Condition
1. Two are playing.
')
2. The game field is a 3 by 3 board.
3. Each player has an army of 100 space marines.
4. Before the battle at night, each side secretly places its units in an arbitrary way on 9 squares. On each cell, you can put any integer number of Space Marines from 0 to 100.
5. The battle for the next planet begins in the morning. On each of the 9 cells, the player who has more Astartes on this cell wins. For winning on each of the 9 cells is given 1 point. If there is an identical number on a certain cell, then the battle on this cell ends in a draw, and both players get 0.5 points.
6. The battle is won by the one who won more fields. If both players have won 4.5 fields, the battle ends in a draw.
')
2. The game field is a 3 by 3 board.
3. Each player has an army of 100 space marines.
4. Before the battle at night, each side secretly places its units in an arbitrary way on 9 squares. On each cell, you can put any integer number of Space Marines from 0 to 100.
5. The battle for the next planet begins in the morning. On each of the 9 cells, the player who has more Astartes on this cell wins. For winning on each of the 9 cells is given 1 point. If there is an identical number on a certain cell, then the battle on this cell ends in a draw, and both players get 0.5 points.
6. The battle is won by the one who won more fields. If both players have won 4.5 fields, the battle ends in a draw.
When I launched this experiment, I still did not know that this game has no perfect solution, but thanks to the comments I was able to better understand this topic.
Let's start with the winners of this game.

Solution Nouneym 4173

The best solution scored 4121 wins - a very good result. But what would happen if solutions from only TOP-100 participated in the game?

Surprisingly, it did not even enter the top5 (in 8th place), and the 1st place here was taken by the decision from 68th place.
Arem Solution

This just shows that there is no better solution. The remaining results can be viewed at game.pavlukhinlab.com
But what else can you learn?
The largest numbers of players were placed in the center, on average, all the players filled the first row with larger numbers, while the best results placed greater emphasis on the bottom row.


average values for all games (left) and TOP-100 (right)
Well, and more examples of the best strategies:
Ogoun strategy examples (6 solutions in TOP-100)



Guten strategy examples (8 solutions in TOP-100)



The best strategies chose 5 main cells, the remaining cells were filled with small values. Which is logical, because for victory, it is enough to take 5 cells.
And now some graphs.
Probability distributions of numbers:


second cells among all players (left) and TOP-100 (right)


central cells among all and TOP-100

number distribution for all games

distribution of numbers on the TOP-100
If you look at the distribution of all cells among all players, then they look generally similar. You can also conclude that in these conditions it makes no sense to fill the cells with values greater than 30.
At this point, the study comes to an end - that's all I could extract from this data. Perhaps some of you will be able to offer something else that can be checked - I am waiting for you in the comments. Impersonal games look for the link .
Py.Sy. In the previous post, I talked about the neuron, which was trained to play this game. Unfortunately, none of this has happened yet. Two neurons decided that the best strategy is to throw zeros at the output and enjoy a draw. But maybe I will understand this topic and make a separate post dedicated to the mistakes that I made when creating a neuron, and, perhaps, success.
Source: https://habr.com/ru/post/441728/
All Articles