How a children's puzzle helps unlock the secrets of magnetism.

Magnets have been familiar to people since ancient times, but the physics of ferromagnetism remains a mystery. Now familiar puzzle brings physicists closer to answering questions.

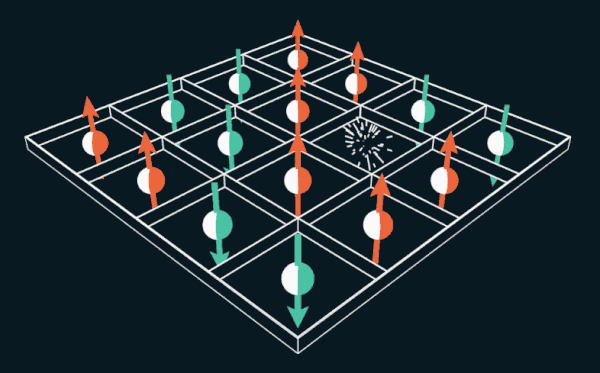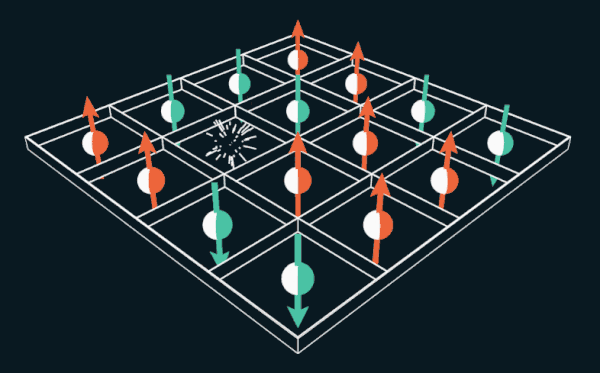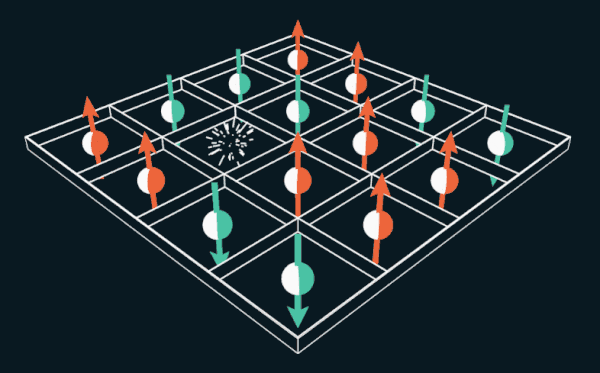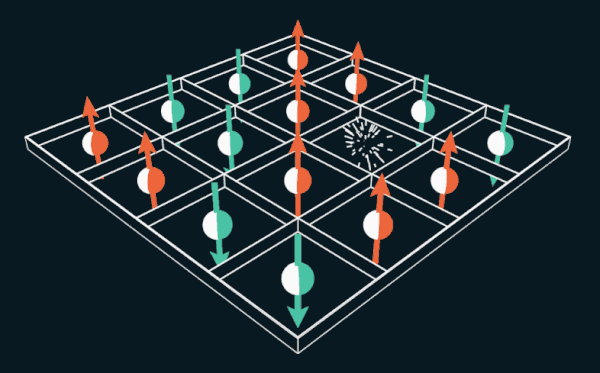
A game of 15 invites the player to move the numbered tiles within the grid. If you replace the numbers with electron spins, the puzzle can be used to explain how permanent magnets work.

For several months in 1880, entire regions of the United States succumbed to addiction, which no one had seen before. "An epidemic literally broke out all over the country," wrote The Weekly News-Democrat magazine in Imporia, Kansas, on March 12, 1880. "Entire cities are lured, people lose their sleep and go crazy." The epidemic spread to Europe, and even reached Australia with New Zealand.

The disease has become a new passion: a discouraging simple mechanical puzzle toy "15". It is still known, and consists of a 4x4 square field in which you can move 15 numbered tiles in order to place them in order.

By today's standards, the game seems old-fashioned, but in 1880 it was at the peak of popularity. “No child will be able to resist such entertainment, no adult will be so strong or arrogant as to avoid her charm,” the newspaper wrote. And disappointment may have stemmed from a mathematically proven fact that only half of the configurations of this puzzle can be successfully solved (which probably was not known to come under its influence).
')
Today, almost 140 years later, interest in the game “15” has been revived again, but this time it acts not as a distraction, but as a way to understand what seems to be unrelated to it and where much more complicated puzzle: how magnets work.

Permanent magnets, such as those that hang on the door of your refrigerator, are attracted due to the phenomenon of ferromagnetism . In a ferromagnet, the spins of electrons are aligned, and collectively generate a magnetic field. More precisely, metals such as iron, cobalt and nickel exhibit band magnetism, since their electrons are able to move freely within the material. Each electron has its own magnetic moment, but to understand how and why all these moments are arranged in a magnet, it is necessary to calculate the quantum interactions between all electrons, which is excessively difficult to do.

“Zonal magnetism is in fact one of the most difficult tasks of theoretical condensed matter physics,” said Wai Lee, a physicist at Johns Hopkins University.

However, Lee and two graduate students, Eric Bobrov and Keaton Steubis, may have come a little closer to solving this problem. Using the mathematics of the puzzle "15", they expanded the well-known theorem describing the idealized state of zonal magnetism. In their new analysis , published in the journal Physical Review B, they expand the theorem to explain a broader and more realistic system, which could potentially lead to the creation of a more accurate model of magnet operation.

“It's a great job,” said Daniel Arovas , a physicist at the University of California, San Diego. “I especially like this work due to the fact that there are too few detailed results regarding zone magnetism and they are too fragmented.”

Jumping over holes

At the most basic level, electrons in a metal must obey two major constraints. First, they are all negatively charged, so they repel each other. Secondly, the electrons must obey the so-called. the Pauli principle postulating that two particles [with half-integer spin / approx. trans.] cannot be in the same quantum state. This means that electrons with the same spin — proportional to the magnetic moment of the electron — cannot occupy the same state in the metal atom. And two electrons with opposite spins can.

It turns out that the simplest way to satisfy simultaneously the mutual repulsion and the limitations of the Pauli principle for a group of electrons will be located separately and align the backs - as a result, the material becomes ferromagnetic.

However, this is only a simplified picture. Physicists in no way could construct a detailed model of the appearance of such an organized pattern of aligned spins from the innumerable quantum interactions between individual electrons. For example, as Lee explained, the wave function of an electron — a complex mathematical description of its quantum properties — may be entangled with the wave function of another electron. In order to thoroughly understand how the behavior of individual particles leads to the emergence of such a collective phenomenon as ferromagnetism, one will have to monitor the wave function of each electron in the system, while it continuously changes the wave function of each of the remaining electrons in the process of their interaction. In practice, such pervasive confusion makes it impossible to write the complete and comprehensive equations necessary to describe ferromagnetism.

Instead, physicists, including Lee, are trying to gather information by studying simplified, idealized models describing the physics underlying ferromagnetism. In particular, her latest work extends an important discovery made over 50 years ago.

In the mid-1960s, two physicists from opposite sides of the globe independently produced a proof explaining why electrons should be aligned and create a ferromagnetic state. David Tules, a physicist who worked at Cambridge University, who would eventually receive the 2016 Nobel Prize, and Josuka Nagaoka, a physicist from Nagoya University, who was visiting at the University of California at San Diego at that time, published their evidence in 1965 and 1966, respectively . Their result, called the Nagaoki – Tules theorem (or simply the Nagaoka theorem), is based on an idealized system of electrons located on an atomic lattice. So, although it does not explain the behavior of real magnets, it was still important, for the first time, in principle, showing why the spins of electrons should align. And since their analysis was a mathematical proof, they were accurate, not burdened with approximations typical of physics.

To understand the theorem, imagine a two-dimensional square lattice. Each site can place two electrons with opposite spins, but the theorem assumes that an infinite amount of energy is required to place two electrons in one place. This ensures that only one electron will be in each place. In this configuration, each electron can direct its spin either up or down. They do not have to level off, so this system should not be a ferromagnet.


Wai Lee, a physicist from Johns Hopkins University

Now remove one electron. As a result, there will be a vacant place called a hole. The neighboring electron can slip into the hole, leaving behind a new empty space. Another electron can move to a new empty space, leaving behind another hole. In this example, the hole, in fact, jumps from one place to another, moving along the grid. Tules and Nagaoka found that in this case, by adding a single hole, the electrons will align spontaneously. They proved that this would be the lowest energy state, the state of a ferromagnet.

Arovas explains that in order for the system to come to a state with the lowest energy, the hole must be able to move freely without disturbing the configuration of the electron spins — such a process will require additional energy. But when the hole moves, the electrons must move. In order for the electrons to move without breaking the configuration of the spins, they must be aligned.

“Nagaoki's theorem is one of the few examples with which you can mathematically prove individual cases of ferromagnetism,” said Masaki Oshikawa , a physicist at Tokyo University. “But from the point of view of physics, all this is very artificial.”

For example, electrons require a lot of energy to overcome their mutual repulsion and get settled in one place - but not infinite, as the theorem requires. In addition, the picture painted by Nagaoka and Tules applies only to simple lattices: two-dimensional lattices consisting of squares or triangles, or three-dimensional cubic lattices. In nature, ferromagnetism occurs in many metals with structures of all kinds.

If the Nagaoki-Tules theorem actually explains ferromagnetism, then it should be applicable to all grids. People assumed it was, Lee said. "But no one gave real, clear evidence." Well, that is, so far.

Back tiles

In 1989, Hal Tasaki, a physicist from the Japanese University Gakushuin, expanded this theorem, finding that it will be applicable as long as the lattice has a mathematical property such as connectivity. Take the simple case of a square lattice with one moving hole. If, by moving the hole, you can reproduce any configuration of the spins, keeping the number of electrons, with the spins directed both up and down, then the condition of connectivity is satisfied.

But besides the square and triangular lattices, and three-dimensional cubes, it was not clear whether the condition of connectivity would be satisfied in other cases — and, therefore, how widely this theorem can be applied.

To deal with this issue, Lee began with a hexagonal grid of cells. Her students, Bobrov and Steubis, working on this task, realized that it resembles a mania of the XIX century: the puzzle "15". Change the labels of the tiles from the numbers to the backs, pointing up and down, and the puzzle becomes equivalent to the Nagaoka ferromagnet, with a hole moving along an electron lattice.

The puzzle is solved when you have the opportunity to redistribute tiles in any sequence, which fully coincides with the condition of connectivity. So the question of whether the condition of connectedness is satisfied for a given lattice becomes the question of whether an equivalent puzzle can be solved on a lattice of such a structure.

It turns out that in 1974, the mathematician Richard Wilson, now working at the California Institute of Technology, solved this problem by summarizing and solving the “15” puzzle for all the grids. As part of the proof, he showed that on almost all inseparable grids (in which all nodes remain connected even after removing one of them), you can move the tiles and get any configuration as long as the number of movements remains even. The only exception is single polygons larger than a triangle, and something called “graph θ zero”, in which the vertex at the center of the hexagon is connected to two opposite vertices.

The researchers were able to directly apply Wilson's proof to the Nagaoki – Tules theorem. They proved that the condition of connectivity is satisfied for a system of electrons and a single hole on almost all lattices, including such common structures as two-dimensional cells and three-dimensional diamond-shaped lattices. Two exceptions — polygons larger than a triangle, and graph θnol — are not found in real ferromagnets anyway.

Hole blast

Using the “15” puzzle is a fresh and potentially fruitful approach, said Sriram Shastri , a physicist at the University of California, Santa Cruz. “I like the fact that he brought to work a new language, a new set of links with graph theory,” he said. “I think this is a rich connection — in the future it can be a rich source of ideas.” But, although the study makes a significant step forward, problems still remain.

One of the complications is due to the fact that the Nagaoka-Tules theorem does not always work when a moving hole needs to take an odd number of steps in the process of moving along the grid, Shastri said. Perhaps the most conspicuous problem is that the theorem requires the presence of exactly one hole — no more, no less. However, metals are full of holes; they often occupy up to half of the lattice.

But physicists tried to generalize the theorem for systems with many holes. Using numerical methods, physicists have shown that Nagaoka ferromagnetism, apparently, works for a square lattice of finite size, up to 30% of which are holes. In their current work, the researchers applied precise analytical techniques to two-dimensional cells and to three-dimensional diamond-shaped grids. Ferromagnetism Nagaoka, apparently, exists as long as the number of holes does not exceed the number of lattice sites to a degree 1/2 for cells, and to a degree 2/5 for a diamond shape lattice.

These exact solutions can lead to the creation of a more complete model of zonal magnetism. “This is just one small step toward setting a rigorous mathematical starting point for future research,” Lee said.