During meshoptimizer development, a question often arises: “Can this algorithm use SIMD?”

The library is performance oriented, but SIMD does not always provide significant speed benefits. Unfortunately, SIMD can make the code less portable and less maintainable. Therefore, in each case it is necessary to seek a compromise. When performance is paramount, separate SIMD implementations have to be developed and maintained for SSE and NEON instruction sets. In other cases, you need to understand what is the effect of the use of SIMD. Today we will try to speed up the sloppy mesh simplifier — a new algorithm recently added to the library — using the SSEn / AVXn instruction sets.



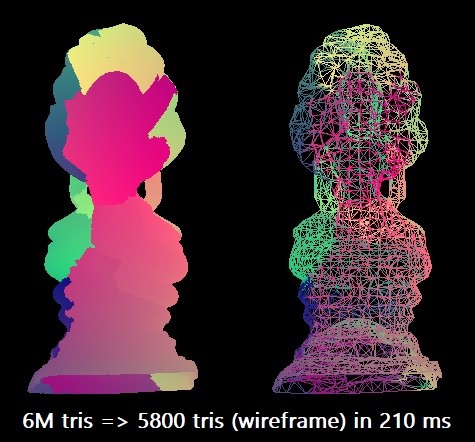
For our benchmark, we simplify the Thai Buddha model from 6 million triangles to 0.1% of this amount. We use the Microsoft Visual Studio 2019 compiler for the target x64 architecture. The scalar algorithm can perform this rationalization in about 210 ms in a single stream of Intel Core i7-8700K (at a frequency of ~ 4.4 GHz). This corresponds to approximately 28.5 million triangles per second. Perhaps in practice this is enough, but I was curious to explore the maximum capabilities of the equipment.
')
In some cases, the procedure can be parallelized by dividing the grid into pieces, but this requires an additional analysis of connectivity in order to preserve the boundaries, so for the time being we restrict ourselves to purely SIMD optimizations.

Seven measurements

To understand the possibilities for optimization, let's perform profiling using Intel VTune. Run the procedure 100 times to ensure that there is enough data.



Here I turned on the micro-architecture mode to fix the execution time of each function, as well as find the bottlenecks. We see that rationalization is performed using a set of functions, each of which requires a certain number of cycles. The list of functions is sorted by time. Here they are in order of execution to make it easier to understand the algorithm:

• rescalePositions normalizes the positions of all vertices into a single cube to prepare for quantization using computeVertexIds
• computeVertexIds computes a 30-bit quantized identifier for each vertex on a uniform grid of a given size, where each axis is quantized on a grid (the grid size is 10 bits, so the identifier is 30)
• countTriangles calculates the approximate number of triangles that the rationalizer will create for a given grid size, assuming that all the vertices are combined in one grid cell
• fillVertexCells fills a table that relates all vertices to the corresponding cells; all vertices with the same ID correspond to the same cell
• fillCellQuadrics fills a Quadric structure (4 × 4 symmetric matrix) for each cell to reflect cumulative information about the corresponding geometry.
• fillCellRemap calculates a vertex index for each cell, selecting one of the vertices in that cell, and minimizes geometric distortion.
• filterTriangles displays the final set of triangles according to the vertex-cell-vertex tables built earlier; A naive translation can produce on average ~ 5% duplicate triangles, so the function filters duplicates.

computeVertexIds and countTriangles are executed several times: the algorithm determines the mesh size for vertex merging, performs an accelerated binary search to reach the target number of triangles (in our case, 6000) and calculates the number of triangles that each mesh size will generate at each iteration. Other functions are run once. In our file, five search passes give a target grid size of 40 ³ .

VTune helpfully reports that the most resource-intensive function is the one that calculates quadrics: it takes almost half of the total execution time of 21 s. This is the first goal for optimizing SIMD.

SIMD bit by bit

Let's look at the source code of fillCellQuadrics to better understand what exactly it calculates:

 static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); float weight = single_cell ? 3.f : 1.f; Quadric Q; quadricFromTriangle(Q, vertex_positions[i0], vertex_positions[i1], vertex_positions[i2], weight); if (single_cell) { quadricAdd(cell_quadrics[c0], Q); } else { quadricAdd(cell_quadrics[c0], Q); quadricAdd(cell_quadrics[c1], Q); quadricAdd(cell_quadrics[c2], Q); } } } 

The function enumerates all the triangles, calculates a quadric for each of them and adds it to the quadrics of each cell. A quadric is a 4 × 4 symmetric matrix, represented as 10 floating-point numbers:

 struct Quadric { float a00; float a10, a11; float a20, a21, a22; float b0, b1, b2, c; }; 

Calculating a quadric requires solving the equation of the plane for a triangle, building a quadratic matrix and weighing it using the area of ​​the triangle:

 static void quadricFromPlane(Quadric& Q, float a, float b, float c, float d) { Q.a00 = a * a; Q.a10 = b * a; Q.a11 = b * b; Q.a20 = c * a; Q.a21 = c * b; Q.a22 = c * c; Q.b0 = d * a; Q.b1 = d * b; Q.b2 = d * c; Qc = d * d; } static void quadricFromTriangle(Quadric& Q, const Vector3& p0, const Vector3& p1, const Vector3& p2, float weight) { Vector3 p10 = {p1.x - p0.x, p1.y - p0.y, p1.z - p0.z}; Vector3 p20 = {p2.x - p0.x, p2.y - p0.y, p2.z - p0.z}; Vector3 normal = { p10.y * p20.z - p10.z * p20.y, p10.z * p20.x - p10.x * p20.z, p10.x * p20.y - p10.y * p20.x }; float area = normalize(normal); float distance = normal.x*p0.x + normal.y*p0.y + normal.z*p0.z; quadricFromPlane(Q, normal.x, normal.y, normal.z, -distance); quadricMul(Q, area * weight); } 

It looks like there are a lot of floating point operations, so they can be parallelized using SIMD. To begin with, we represent each vector as 4-wide SIMD vectors, and also change the Quadric structure to 12 floating point numbers instead of 10, so that it fits smoothly into the three SIMD registers (increasing the size does not affect performance) and change the field order to calculate in quadricFromPlane become more uniform:

 struct Quadric { float a00, a11, a22; float pad0; float a10, a21, a20; float pad1; float b0, b1, b2, c; }; 

Here, some calculations, in particular, the scalar product, do not correspond much to earlier versions of SSE. Fortunately, in SSE4.1 appeared instruction for the scalar product, which is very useful to us.

 static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { const int yzx = _MM_SHUFFLE(3, 0, 2, 1); const int zxy = _MM_SHUFFLE(3, 1, 0, 2); const int dp_xyz = 0x7f; for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); __m128 p0 = _mm_loadu_ps(&vertex_positions[i0].x); __m128 p1 = _mm_loadu_ps(&vertex_positions[i1].x); __m128 p2 = _mm_loadu_ps(&vertex_positions[i2].x); __m128 p10 = _mm_sub_ps(p1, p0); __m128 p20 = _mm_sub_ps(p2, p0); __m128 normal = _mm_sub_ps( _mm_mul_ps( _mm_shuffle_ps(p10, p10, yzx), _mm_shuffle_ps(p20, p20, zxy)), _mm_mul_ps( _mm_shuffle_ps(p10, p10, zxy), _mm_shuffle_ps(p20, p20, yzx))); __m128 areasq = _mm_dp_ps(normal, normal, dp_xyz); // SSE4.1 __m128 area = _mm_sqrt_ps(areasq); // masks the result of the division when area==0 // scalar version does this in normalize() normal = _mm_and_ps( _mm_div_ps(normal, area), _mm_cmpneq_ps(area, _mm_setzero_ps())); __m128 distance = _mm_dp_ps(normal, p0, dp_xyz); // SSE4.1 __m128 negdistance = _mm_sub_ps(_mm_setzero_ps(), distance); __m128 normalnegdist = _mm_blend_ps(normal, negdistance, 8); __m128 Qx = _mm_mul_ps(normal, normal); __m128 Qy = _mm_mul_ps( _mm_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 2, 2, 1)), _mm_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 0, 1, 0))); __m128 Qz = _mm_mul_ps(negdistance, normalnegdist); if (single_cell) { area = _mm_mul_ps(area, _mm_set1_ps(3.f)); Qx = _mm_mul_ps(Qx, area); Qy = _mm_mul_ps(Qy, area); Qz = _mm_mul_ps(Qz, area); Quadric& q0 = cell_quadrics[c0]; __m128 q0x = _mm_loadu_ps(&q0.a00); __m128 q0y = _mm_loadu_ps(&q0.a10); __m128 q0z = _mm_loadu_ps(&q0.b0); _mm_storeu_ps(&q0.a00, _mm_add_ps(q0x, Qx)); _mm_storeu_ps(&q0.a10, _mm_add_ps(q0y, Qy)); _mm_storeu_ps(&q0.b0, _mm_add_ps(q0z, Qz)); } else { // omitted for brevity, repeats the if() body // three times for c0/c1/c2 } } } 

This code is nothing particularly interesting; we use abundantly unaligned load / store instructions here. Although the input data of Vector3 can be aligned, but there seems to be no noticeable penalty for unaligned reads. Note that in the first half of the function the vectors are not used, which is good - our vectors have three components, and in some cases only one (see the calculation areasq / area / distance), while the processor performs 4 operations in parallel. In any case, let's see how parallelization helped.



A hundred fillCellQuadrics launches fillCellQuadrics now done in 5.3 seconds instead of 9.8 seconds, which saves about 45 ms for each operation — not bad, but not very impressive. In many instructions we use three instead of four components, as well as precise multiplication, which gives a rather significant delay. If you have previously written instructions for SIMD, then you know how to properly do the scalar product.

To do this, you need to do four vectors at once. Instead of storing one full vector in one SIMD register, we use three registers - in one we store four components x , in the other we will store , and in the third z . Here we need four vectors for work at once: it means that we will process four triangles simultaneously.

We have a lot of arrays with dynamic indexing. It usually helps to pre-transfer data to prepared x / y / z component arrays (or rather, small SIMD registers are usually used, for example, float x[8], y[8], z[8] , for each of the 8 vertices in the input data: this is called AoSoA (arrays of array structures) and gives a good balance between cache locality and ease of loading into SIMD registers), but here dynamic indexing does not work very well, so we load data for four triangles as usual, and transpose vectors with the help of macro _MM_TRANSPOSE .

Theoretically, we need to calculate each component of four finite quadrics in its own SIMD register (for example, we will have __m128 Q_a00 with four components a00 finite quadrics). In this case, the operations on quadrics fit the 4-wide SIMD instructions quite well, and the transformation actually slows down the code - so we transpose only the initial vectors, and then transpose back the equations of the plane and run the same code that was used to calculate the quadrics, but we repeat it four times. Here's what the code looks like, which then calculates the equations for the plane (the remaining parts are omitted for brevity):

 unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; unsigned int i20 = indices[(i + 2) * 3 + 0]; unsigned int i21 = indices[(i + 2) * 3 + 1]; unsigned int i22 = indices[(i + 2) * 3 + 2]; unsigned int i30 = indices[(i + 3) * 3 + 0]; unsigned int i31 = indices[(i + 3) * 3 + 1]; unsigned int i32 = indices[(i + 3) * 3 + 2]; // load first vertex of each triangle and transpose into vectors with components (pw0 isn't used later) __m128 px0 = _mm_loadu_ps(&vertex_positions[i00].x); __m128 py0 = _mm_loadu_ps(&vertex_positions[i10].x); __m128 pz0 = _mm_loadu_ps(&vertex_positions[i20].x); __m128 pw0 = _mm_loadu_ps(&vertex_positions[i30].x); _MM_TRANSPOSE4_PS(px0, py0, pz0, pw0); // load second vertex of each triangle and transpose into vectors with components __m128 px1 = _mm_loadu_ps(&vertex_positions[i01].x); __m128 py1 = _mm_loadu_ps(&vertex_positions[i11].x); __m128 pz1 = _mm_loadu_ps(&vertex_positions[i21].x); __m128 pw1 = _mm_loadu_ps(&vertex_positions[i31].x); _MM_TRANSPOSE4_PS(px1, py1, pz1, pw1); // load third vertex of each triangle and transpose into vectors with components __m128 px2 = _mm_loadu_ps(&vertex_positions[i02].x); __m128 py2 = _mm_loadu_ps(&vertex_positions[i12].x); __m128 pz2 = _mm_loadu_ps(&vertex_positions[i22].x); __m128 pw2 = _mm_loadu_ps(&vertex_positions[i32].x); _MM_TRANSPOSE4_PS(px2, py2, pz2, pw2); // p1 - p0 __m128 px10 = _mm_sub_ps(px1, px0); __m128 py10 = _mm_sub_ps(py1, py0); __m128 pz10 = _mm_sub_ps(pz1, pz0); // p2 - p0 __m128 px20 = _mm_sub_ps(px2, px0); __m128 py20 = _mm_sub_ps(py2, py0); __m128 pz20 = _mm_sub_ps(pz2, pz0); // cross(p10, p20) __m128 normalx = _mm_sub_ps( _mm_mul_ps(py10, pz20), _mm_mul_ps(pz10, py20)); __m128 normaly = _mm_sub_ps( _mm_mul_ps(pz10, px20), _mm_mul_ps(px10, pz20)); __m128 normalz = _mm_sub_ps( _mm_mul_ps(px10, py20), _mm_mul_ps(py10, px20)); // normalize; note that areasq/area now contain 4 values, not just one __m128 areasq = _mm_add_ps( _mm_mul_ps(normalx, normalx), _mm_add_ps( _mm_mul_ps(normaly, normaly), _mm_mul_ps(normalz, normalz))); __m128 area = _mm_sqrt_ps(areasq); __m128 areanz = _mm_cmpneq_ps(area, _mm_setzero_ps()); normalx = _mm_and_ps(_mm_div_ps(normalx, area), areanz); normaly = _mm_and_ps(_mm_div_ps(normaly, area), areanz); normalz = _mm_and_ps(_mm_div_ps(normalz, area), areanz); __m128 distance = _mm_add_ps( _mm_mul_ps(normalx, px0), _mm_add_ps( _mm_mul_ps(normaly, py0), _mm_mul_ps(normalz, pz0))); __m128 negdistance = _mm_sub_ps(_mm_setzero_ps(), distance); // this computes the plane equations (a, b, c, d) for each of the 4 triangles __m128 plane0 = normalx; __m128 plane1 = normaly; __m128 plane2 = normalz; __m128 plane3 = negdistance; _MM_TRANSPOSE4_PS(plane0, plane1, plane2, plane3); 

The code is a little longer: now we process four triangles in each iteration, and we no longer need SSE4.1 instructions for this. In theory, SIMD units should be used more efficiently. Let's see how it helped.



Well, no big deal. The code has accelerated very slightly, although the fillCellQuadrics function fillCellQuadrics now performed almost twice as fast as the original function without SIMD, but it is unclear whether this significant increase in complexity justifies. Theoretically, you can use AVX2 and process 8 triangles per iteration, but here you will need to spin the loop even more manually (ideally, all this code is generated using ISPC, but my naive attempts to make it generate good code did not lead to success: instead of load / store sequences he insisted on gather / scatter, which significantly slows down the execution). Let's try something else.

AVX2 = SSE2 + SSE2

AVX2 - a bit peculiar set of instructions. It has 8-wide floating point registers, and one instruction can perform 8 operations; but essentially this instruction is not different from two SSE2 instructions executed on two half of the register (as far as I understand, the first processors with AVX2 support decoded each instruction into two or more microoperations, therefore the performance increase was limited by the phase of extracting instructions). For example, _mm_dp_ps performs a scalar product between two SSE2 registers, and _mm256_dp_ps produces two scalar products between the two halves of two AVX2 registers, therefore limited to 4-wide for each half.

Because of this, the AVX2 code often differs from the universal “8-wide SIMD”, but here it works in our favor: instead of trying to improve vectorization by transposing 4-wide vectors, we return to the first SIMD version and unwind the cycle twice using AVX2 instructions instead of SSE2 / SSE4. We still need to load and store 4-wide vectors, but in general we simply change in the code __m128 to __m256 and _mm_ to _mm256 with several settings:

 unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; __m256 p0 = _mm256_loadu2_m128( &vertex_positions[i10].x, &vertex_positions[i00].x); __m256 p1 = _mm256_loadu2_m128( &vertex_positions[i11].x, &vertex_positions[i01].x); __m256 p2 = _mm256_loadu2_m128( &vertex_positions[i12].x, &vertex_positions[i02].x); __m256 p10 = _mm256_sub_ps(p1, p0); __m256 p20 = _mm256_sub_ps(p2, p0); __m256 normal = _mm256_sub_ps( _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, yzx), _mm256_shuffle_ps(p20, p20, zxy)), _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, zxy), _mm256_shuffle_ps(p20, p20, yzx))); __m256 areasq = _mm256_dp_ps(normal, normal, dp_xyz); __m256 area = _mm256_sqrt_ps(areasq); __m256 areanz = _mm256_cmp_ps(area, _mm256_setzero_ps(), _CMP_NEQ_OQ); normal = _mm256_and_ps(_mm256_div_ps(normal, area), areanz); __m256 distance = _mm256_dp_ps(normal, p0, dp_xyz); __m256 negdistance = _mm256_sub_ps(_mm256_setzero_ps(), distance); __m256 normalnegdist = _mm256_blend_ps(normal, negdistance, 0x88); __m256 Qx = _mm256_mul_ps(normal, normal); __m256 Qy = _mm256_mul_ps( _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 2, 2, 1)), _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 0, 1, 0))); __m256 Qz = _mm256_mul_ps(negdistance, normalnegdist); 

Here you can take every 128-bit half of the received Qx / Qz / Qz and run the same code that we used to add quadrics. Instead, we assume that if a triangle has three vertices in one cell ( single_cell == true value single_cell == true ), then it is very likely that the other triangle also has three vertices in another cell, and produce a final aggregation of quadrics also using AVX2:

 unsigned int c00 = vertex_cells[i00]; unsigned int c01 = vertex_cells[i01]; unsigned int c02 = vertex_cells[i02]; unsigned int c10 = vertex_cells[i10]; unsigned int c11 = vertex_cells[i11]; unsigned int c12 = vertex_cells[i12]; bool single_cell = (c00 == c01) & (c00 == c02) & (c10 == c11) & (c10 == c12); if (single_cell) { area = _mm256_mul_ps(area, _mm256_set1_ps(3.f)); Qx = _mm256_mul_ps(Qx, area); Qy = _mm256_mul_ps(Qy, area); Qz = _mm256_mul_ps(Qz, area); Quadric& q00 = cell_quadrics[c00]; Quadric& q10 = cell_quadrics[c10]; __m256 q0x = _mm256_loadu2_m128(&q10.a00, &q00.a00); __m256 q0y = _mm256_loadu2_m128(&q10.a10, &q00.a10); __m256 q0z = _mm256_loadu2_m128(&q10.b0, &q00.b0); _mm256_storeu2_m128(&q10.a00, &q00.a00, _mm256_add_ps(q0x, Qx)); _mm256_storeu2_m128(&q10.a10, &q00.a10, _mm256_add_ps(q0y, Qy)); _mm256_storeu2_m128(&q10.b0, &q00.b0, _mm256_add_ps(q0z, Qz)); } else { // omitted for brevity } 

The resulting code is simpler, more concise and faster than our unsuccessful SSE2 approach:



Of course, we did not achieve acceleration 8 times, but only 2.45 times. The load and store operations are still 4-wide, since we are forced to work with an awkward memory layout due to dynamic indexing, and the calculations are not optimal for SIMD. But now fillCellQuadrics no longer a bottleneck in our profile pipeline, and you can focus on other features.

Gather around children

We saved 4.8 seconds on the test run (48 ms on each run), and now our main violator is countTriangles . It would seem a simple function, but it is executed not once, but five times:

 static size_t countTriangles(const unsigned int* vertex_ids, const unsigned int* indices, size_t index_count) { size_t result = 0; for (size_t i = 0; i < index_count; i += 3) { unsigned int id0 = vertex_ids[indices[i + 0]]; unsigned int id1 = vertex_ids[indices[i + 1]]; unsigned int id2 = vertex_ids[indices[i + 2]]; result += (id0 != id1) & (id0 != id2) & (id1 != id2); } return result; } 

The function enumerates all source triangles and calculates the number of non-degenerate triangles comparing the identifiers of the vertices. It is not immediately clear how to parallelize it using SIMD ... unless you use the gather instructions.

AVX2 instruction set added to x64 SIMD collection / scatter instruction family; each of them accepts a vector register with 4 or 8 values ​​- and simultaneously performs 4 or 8 load or save operations. If you use here, you can download three indexes, gather all at once (or in groups of 4 or 8) and compare the results. Gather on Intel processors has historically been rather slow, but let's try. For simplicity, let's load the data for 8 triangles, transpose vectors like our previous attempt, and compare the corresponding elements of each vector:

 for (size_t i = 0; i < (triangle_count & ~7); i += 8) { __m256 tri0 = _mm256_loadu2_m128( (const float*)&indices[(i + 4) * 3 + 0], (const float*)&indices[(i + 0) * 3 + 0]); __m256 tri1 = _mm256_loadu2_m128( (const float*)&indices[(i + 5) * 3 + 0], (const float*)&indices[(i + 1) * 3 + 0]); __m256 tri2 = _mm256_loadu2_m128( (const float*)&indices[(i + 6) * 3 + 0], (const float*)&indices[(i + 2) * 3 + 0]); __m256 tri3 = _mm256_loadu2_m128( (const float*)&indices[(i + 7) * 3 + 0], (const float*)&indices[(i + 3) * 3 + 0]); _MM_TRANSPOSE8_LANE4_PS(tri0, tri1, tri2, tri3); __m256i i0 = _mm256_castps_si256(tri0); __m256i i1 = _mm256_castps_si256(tri1); __m256i i2 = _mm256_castps_si256(tri2); __m256i id0 = _mm256_i32gather_epi32((int*)vertex_ids, i0, 4); __m256i id1 = _mm256_i32gather_epi32((int*)vertex_ids, i1, 4); __m256i id2 = _mm256_i32gather_epi32((int*)vertex_ids, i2, 4); __m256i deg = _mm256_or_si256( _mm256_cmpeq_epi32(id1, id2), _mm256_or_si256( _mm256_cmpeq_epi32(id0, id1), _mm256_cmpeq_epi32(id0, id2))); result += 8 - _mm_popcnt_u32(_mm256_movemask_epi8(deg)) / 4; } 

The _MM_TRANSPOSE8_LANE4_PS macro in AVX2 is equivalent to _MM_TRANSPOSE4_PS , which is not in the standard header, but is easily displayed. It accepts four AVX2 vectors and transposes two 4 × 4 matrices independently of each other:

 #define _MM_TRANSPOSE8_LANE4_PS(row0, row1, row2, row3) \ do { \ __m256 __t0, __t1, __t2, __t3; \ __t0 = _mm256_unpacklo_ps(row0, row1); \ __t1 = _mm256_unpackhi_ps(row0, row1); \ __t2 = _mm256_unpacklo_ps(row2, row3); \ __t3 = _mm256_unpackhi_ps(row2, row3); \ row0 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(1, 0, 1, 0)); \ row1 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(3, 2, 3, 2)); \ row2 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(1, 0, 1, 0)); \ row3 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(3, 2, 3, 2)); \ } while (0) 

Because of some features in the SSE2 / AVX2 instruction sets, we must use floating-point register operations when transposing vectors. We here load the data a bit carelessly; but it basically doesn’t matter, because we are limited by the performance of the gather:



Now countTriangles works about 27% faster, and notice the terrible CPI (cycles per instruction): we send about four times fewer instructions, but the gather takes a lot of time. It's great that it speeds up the overall work, but, of course, the performance gain is somewhat depressing. We managed to overtake fillCellQuadrics in the profile, which brings us to the last function at the top of the list, which we have not yet looked at.

Chapter 6, where everything starts to work as it should

The last function is computeVertexIds . In the algorithm, it is executed 6 times, therefore it is also an excellent target for optimization. For the first time, we see a function that seems to be created for precise optimization in SIMD:

 static void computeVertexIds(unsigned int* vertex_ids, const Vector3* vertex_positions, size_t vertex_count, int grid_size) { assert(grid_size >= 1 && grid_size <= 1024); float cell_scale = float(grid_size - 1); for (size_t i = 0; i < vertex_count; ++i) { const Vector3& v = vertex_positions[i]; int xi = int(vx * cell_scale + 0.5f); int yi = int(vy * cell_scale + 0.5f); int zi = int(vz * cell_scale + 0.5f); vertex_ids[i] = (xi << 20) | (yi << 10) | zi; } } 

After previous optimizations, we know what needs to be done: spin the loop 4 or 8 times, since there is no point in trying to speed up only one iteration, transpose the vector components and run the calculations in parallel. We do this using AVX2, processing 8 vertices at a time:

 __m256 scale = _mm256_set1_ps(cell_scale); __m256 half = _mm256_set1_ps(0.5f); for (size_t i = 0; i < (vertex_count & ~7); i += 8) { __m256 vx = _mm256_loadu2_m128( &vertex_positions[i + 4].x, &vertex_positions[i + 0].x); __m256 vy = _mm256_loadu2_m128( &vertex_positions[i + 5].x, &vertex_positions[i + 1].x); __m256 vz = _mm256_loadu2_m128( &vertex_positions[i + 6].x, &vertex_positions[i + 2].x); __m256 vw = _mm256_loadu2_m128( &vertex_positions[i + 7].x, &vertex_positions[i + 3].x); _MM_TRANSPOSE8_LANE4_PS(vx, vy, vz, vw); __m256i xi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vx, scale), half)); __m256i yi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vy, scale), half)); __m256i zi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vz, scale), half)); __m256i id = _mm256_or_si256( zi, _mm256_or_si256( _mm256_slli_epi32(xi, 20), _mm256_slli_epi32(yi, 10))); _mm256_storeu_si256((__m256i*)&vertex_ids[i], id); } 

:



computeVertexIds . 120 , 50 . .

, : computeVertexIds ? , , .

computeVertexIds : , . 3 , 12 4 .

100 1,8 , 21 7 . 28 1,46 19 /. , memcmp(block1, block2, 512 MB) . — 45 , 22 / ( AIDA64 31 /, ). , , , 12 .

Conclusion

, 28 , SSE AVX, , 50 . SIMD: 3-wide , SoA-, AVX2- 3-wide , gather , , AVX2 .

SIMD : - . - , , SIMD — , .

, meshoptimizer : , , , . , . ; meshoptimizer 99ab49 , Thai Buddha Sketchfab .