Relational programming: pain, interest, and pain again
In the previous post, we talked in detail about what we were teaching students in the “Industrial Programming” direction. For those whose area of interest lies in a more theoretical field, for example, attract new programming paradigms or abstract mathematics used in theoretical studies on programming, there is another specialization - “Programming Languages”.
Today I will talk about my research in the field of relational programming, which I do at the university and as a student-researcher in the laboratory of language tools JetBrains Research.
What is relational programming? Usually we run the function with arguments and get the result. And in the relational case, you can do the opposite: fix the result and one argument, and get the second argument. The main thing is to write the code correctly and have patience or a good cluster.
')

My name is Dmitry Rozplokhas, I am a first-year postgraduate student at the St. Petersburg Higher School, and last year I graduated from the Bachelor of Academic University with a degree in Programming Languages. From the third year of a bachelor degree I am also a research student in the laboratory of language tools JetBrains Research.
Relational programming is when instead of functions you describe the relationship between the arguments and the result. If the language for this is sharpened, you can get certain bonuses, for example, the ability to run a function in the opposite direction (by the result, restore the possible values of the arguments).
In general, this can be done in any logical language, but interest in relational programming arose simultaneously with the appearance of the minimalistic pure logical language miniKanren about ten years ago, which made it possible to conveniently describe and use similar relationships.
Here are some of the most advanced examples of use: you can write a proof checker and use it to search for evidence ( Near et al., 2008 ) or create an interpreter of a language and use it to generate test suite programs ( Byrd et al., 2017 ).
miniKanren is a small language; only basic mathematical constructions are used to describe relationships. This is an embeddable language, its primitives are a library for some external language, and small programs on miniKanren can be used inside programs in another language.
External languages suitable for miniKanren, a whole bunch. Originally, it was Scheme, we work with the version for Ocaml ( OCanren ), and the full list can be viewed at minikanren.org . Examples in this article will also be on OCanren. Many implementations add helper functions, but we will focus only on the core language.
Let's start with the data types. Conventionally, they can be divided into two types:
For example, if we want to work with arrays in miniKanren itself, then it should be described in terms of terms, by analogy with functional languages - as a simply linked list. A list is either an empty list (denoted by some simple term), or a pair from the first element of the list (“head”) and the rest of the elements (“tail”).
The program in the language miniKanren is the ratio between some variables. When you start the program gives all possible values of variables in general. Often, implementations allow you to limit the number of answers in the output, for example, to find only the first — the search does not always stop after finding all the solutions.
You can write several relations, which are defined through each other and even called recursively, as functions. For example, below, instead of the function define the relationship : list is a concatenation of lists and . Functions that return relationships traditionally end with an “o” to distinguish them from ordinary functions.
The relationship is recorded as some statement regarding its arguments. We have four basic operations :
An attitude can call itself recursively. For example, the “element is on the list. ” We will solve this problem through the analysis of trivial cases, as in functional languages:
The basic version of the language is based on these four operations. There are also extensions that allow other operations to be used. The most useful of them is the disequality constraint for specifying the inequality of two terms (= / =).
Despite its minimalism, miniKanren is quite an expressive language. Here, for example, looks like the relational concatenation of two lists. The function of the two arguments turns into a triple relation " is a concatenation of lists and ".
The solution is not structurally different from how we would write it in a functional language. We parse two cases combined by a disjunction:
We can make a request to this relation, fixing the first and second argument - we get the concatenation of lists:
⇒
We can fix the last argument - we get all the breaks in this list into two.
⇒
Anything else is possible. A slightly more non-standard example in which we fix only part of the arguments:
⇒
From the point of view of the theory, there is nothing impressive here: you can always simply run through all possible options for all arguments, checking for each set whether they behave with respect to a given function / relationship as we would like (see “British Museum Algorithm” ) . It is interesting that here the search (in other words, the search for a solution) uses exclusively the structure of the described relation, due to which it can be relatively effective in practice.
The search goes against accumulating information about various variables in the current state. We either know nothing about each variable, or we know how it is expressed in terms of terms, values, and other variables. For example:
Going through unification, we look at two terms with this information in mind and either update the state or stop searching if two terms cannot be unified. For example, having executed unification b = c, we will receive new information: x = 10, y = z. But the unification b = Nil will cause a contradiction.
We perform a search in conjunctions sequentially (so that information accumulates), and in a disjunction we divide the search into two parallel branches and move on, alternating steps in them - this is the so-called interleaving search. Thanks to this alternation, the search is complete - every suitable solution will be found in a finite time. For example, in the Prolog language this is not the case. Something like a depth traversal (which may hang on an endless branch) is performed there, and the interleaving search is essentially a tricky modification of the width traversal.
Let's now see how the first request from the previous section works. Since appendo has recursive calls, we will add indices to variables to distinguish them. The figure below shows the search tree. The arrows indicate the direction of information dissemination (except for the return from recursion). Between disjunctions, information is not distributed, but between conjunctions it spreads from left to right.

As always: they promise you that everything will be super declarative, but in fact you need to adapt to the language and write everything in a special way (keeping in mind how everything will be executed) so that at least something other than the simplest examples will work. It is disappointing.
One of the first problems that a novice miniKanren programmer faces is that everything depends very much on the order in which you describe the conditions (conjuncts) in the program. With one order, everything is OK, but they changed two conjuncts in places and everything began to work very slowly or not at all. This was unexpected.
Even in the example with appendo, the launch in the opposite direction (the generation of the list splits into two) does not end unless you explicitly indicate how many answers you want (then the search will be terminated after the required number has been found).
Suppose we fix the source variables like this: a =?, B =?, Ab = [1, 2, 3] (see figure below) In the second branch, in a recursive call, this information will not be used in any way (the variable ab and restrictions on and appear only after this call). Therefore, the first recursive call, all its arguments will be free variables. This call will generate all sorts of triples from two lists and their concatenation (and this generation will never end), and then among them will be selected those for which the third element has turned out exactly the way we need.

Everything is not as bad as it may seem at first glance, because we will sort out these triples in large groups. Lists with the same length, but different elements, are in no way different from the point of view of the function, therefore they will fall into one solution - in place of the elements will be free variables. Nevertheless, we will still sort out all possible lengths of the lists, although we only need one, and we know which one. This is a very irrational use (non-use) of information when searching.
This particular example is easy to fix: you just need to transfer the recursive call to the end and everything will work as it should. Before the recursive call, there will be a unification with the variable ab and a recursive call will be made from the tail of this list (as a normal recursive function). This definition with a recursive call at the end will work well in all directions: for a recursive call we manage to accumulate all possible information about the arguments.
However, in any slightly more complicated example, when there are several meaningful challenges, there is no one specific order for which everything will be fine. The simplest example: expanding a list using concatenation. We fix the first argument - this is the order we need, we fix the second - we need to swap calls. Otherwise, it is searched for a long time and the search does not end.
This happens because interleaving search processes the conjuncts consistently, and how to do it differently, without losing the acceptable efficiency, no one could think of it, although they tried. Of course, all the solutions will someday be found, but with the wrong order, they will be searched for so unrealistically long that there is no practical sense in this.
There are techniques for writing programs to avoid this problem. But many of them require special skill and imagination to use, and the result is very large programs. An example is the term size bounding technique and the definition of binary division with the remainder through multiplication with its help. Instead of stupidly writing a mathematical definition
I have to write a recursive definition for 20 lines + a large auxiliary function that cannot be read (I still do not understand what is being done there). It can be found in Will Byrd’s dissertation in the Pure Binary Arithmetic section.
In view of the foregoing, I want to come up with some sort of search modification so that simply and naturally written programs also work.
We noticed that when everything is bad, the search will not be completed unless you explicitly indicate the number of answers and do not interrupt it. Therefore, we decided to fight precisely with the incompleteness of the search - it is much easier to concretize than “it takes a long time”. In general, of course, I just want to speed up the search, but it is much more difficult to formalize, so we started with a less ambitious task.
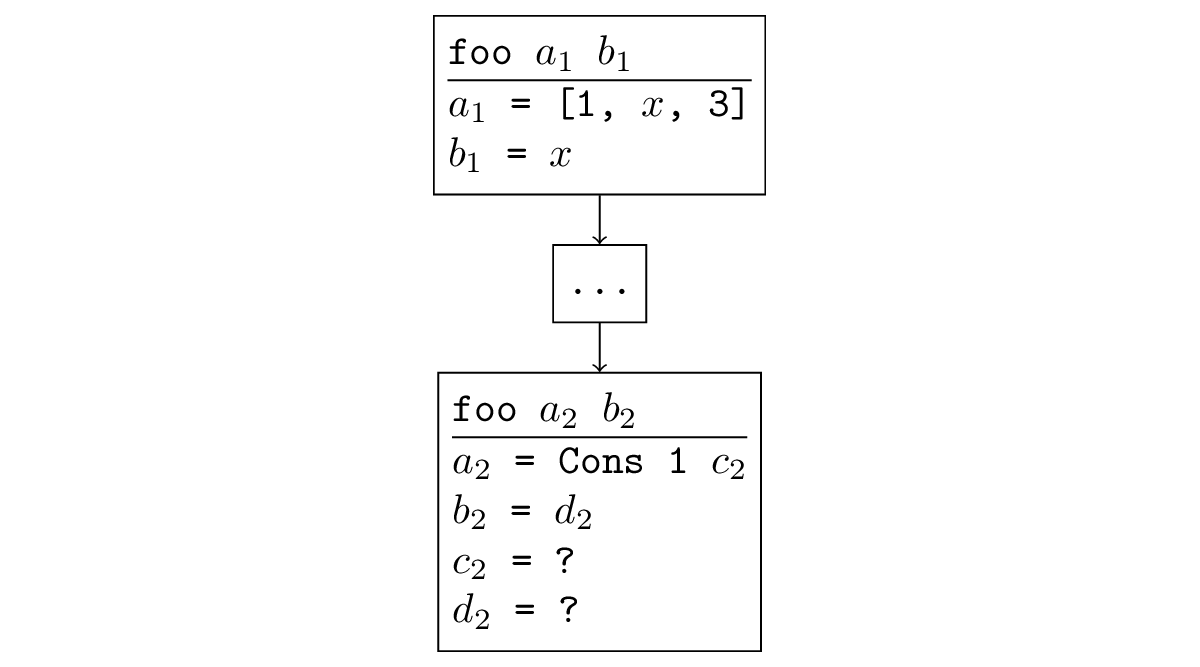
In most cases, when the search diverges, a situation occurs that is easy to track. If some function is called recursively, and when we call the argument recursively, we have the same or less specific arguments, then in the recursive call another such subtask is generated again and endless recursion occurs. Formally, it sounds like this: there is a substitution, applying it to the new arguments, we get the old ones. For example, in the figure below, a recursive call is a generalization of the original: you can substitute = [x, 3], = x and get the original call.
It can be traced that such a situation happens in the examples of divergence we have already encountered. As I wrote earlier, when appendo is started in the opposite direction, a recursive call will be made with free variables instead of all variables, which, of course, is less specific than the original call, in which the third argument was fixed.
If we run reverso with arguments x =? and xr = [1, 2, 3], then it can be traced that the first recursive call will again occur with two free variables, so the new arguments can again be translated into previous ones in an obvious way.
Using this criterion, we can detect the divergence in the process of program execution, understand that everything is bad with this order, and dynamically change it to another one. Due to this, ideally, for each call just the necessary order will be selected.
You can do this naively: if there is a divergence in the conjunct, then we hammer on all the answers that he has already found and postpone his execution for later, “skipping ahead” the next conjunct. Then, perhaps, when we will execute it further, more information will be known already and there will be no divergence. In our examples, this will lead to exactly the desired swap of the conjuncts.
There are less naive ways that allow, for example, not to lose the work already done, postponing execution. Already with the most blunt variant of changing the order, the divergence disappeared in all simple examples suffering from conjunction noncommutativity, which we know, including:
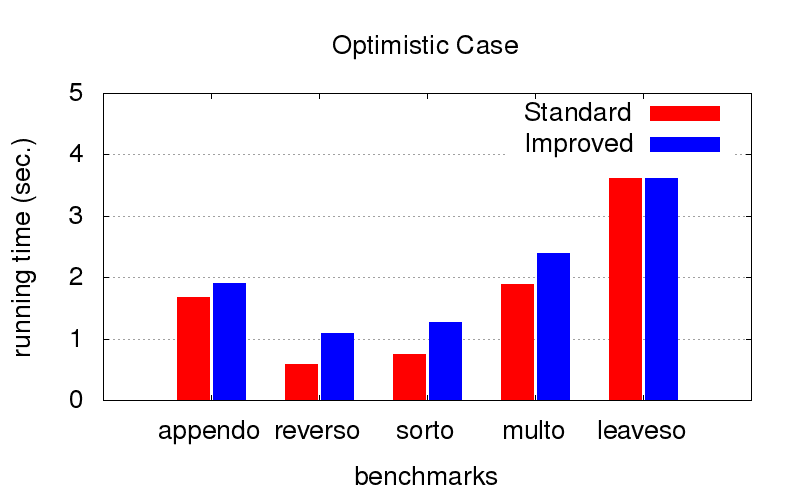
This turned out to be an unexpected surprise for us. In addition to divergence, optimization also struggles with the inhibition of programs. The diagrams below show the execution time of programs with two different orders in conjunctions (relatively speaking, one very good and one of many bad ones). It was launched on a computer with an Intel Core i7 CPU M 620, 2.67GHz x 4, 8GB RAM configuration with Ubuntu 16.04 operating system.
When the order is optimal (we pick it up with our hands), optimization slows down the execution a bit, but is not critical
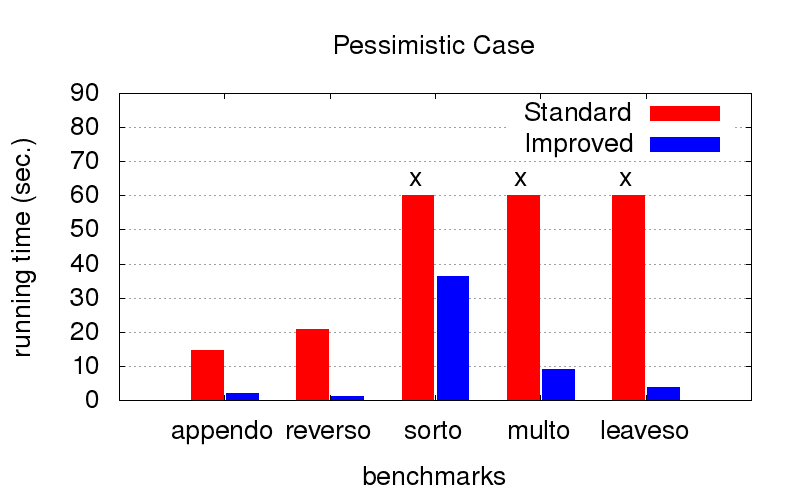
But when the order is not optimal (for example, suitable only for launching in the other direction), with optimization it turns out much faster. Crosses mean that we just could not wait for the end, it works much longer
All this was based purely on intuition and we wanted to prove it strictly. The theory is all the same.
In order to prove something, we need the formal semantics of the language. We described the operational semantics for miniKanren. This is a simplified and mathematical version of the real implementation of the language. It uses a very limited (therefore, easy to use) version in which you can specify only the terminating execution of programs (the search must be finite). But for our purposes, this is exactly what is needed.
To prove the criterion, a lemma is first formulated: the execution of a program from a more general state will work longer. Formally: the output tree in semantics has a great height. This is proved by induction, but we must very carefully generalize the statement, otherwise the inductive hypothesis will not be strong enough. It follows from this lemma that if during the execution of the program the criterion worked, then the output tree has its own subtree greater or equal in height. This is a contradiction, since for inductively defined semantics all trees are finite. This means that in our semantics the execution of this program is inexpressible, which means that the search in it does not end.
The proposed method is conservative: we change something only when we are convinced that everything is already very bad and impossible to do, therefore we do not break anything in terms of the completeness of the programs.
The main evidence contains quite a lot of details, so we had the desire to formally verify it by writing to Coq . However, it turned out to be quite difficult technically, so we cooled our ardor and seriously engaged in automatic verification only in the magistracy.
In the middle of the paper, we presented this study at the ICFP-2017 poster session at the Student Research Competition . There we met the creators of the language, Will Byrd and Daniel Friedman, and they said it was meaningful and we need to look at it in more detail. By the way, Will is generally friends with our laboratory at JetBrains Research. All miniKanren research began with us when, in 2015, Will held a summer school on relational programming in St. Petersburg.
A year later, we brought our work to a more or less complete form and presented an article at the Conference Principles and Practice of Declarative Programming 2018.
We wanted to continue to engage in formal semantics for miniKanren and rigorous evidence of all its properties. In the literature, usually properties (often far from obvious) are simply postulated and demonstrated by examples, but no one proves anything. For example, the main book on relational programming is a list of questions and answers, each of which is devoted to a particular piece of code. Even for the statement about the completeness of interleaving search (and this is one of the most important advantages of miniKanren over a standard Prolog), it is impossible to find a rigorous formulation. We cannot live like this, we decided, and, having received a blessing from Will, set to work.
Let me remind you that the semantics developed by us at the previous stage had a significant limitation: only programs with a finite search were described. In miniKanren, incomplete programs are also of interest, because they can list an infinite number of answers. Therefore, we needed steeper semantics.
There are many different standard ways of defining the semantics of a programming language; we only needed to choose one of them and adapt it to a specific case. We described the semantics as a labeled transition system — a set of possible states in the search process and transitions between these states, some of which are marked with, which means that at this stage of the search there was another answer. The execution of a particular program is thus determined by the sequence of such transitions. These sequences can be finite (coming to a terminal state) or infinite, describing simultaneously terminating and incomplete programs. In order to strictly mathematically set such an object, you need to use a co-inductive definition.
The semantics described above is operational - it reflects the real implementation of the search. In addition to it, we also use denotational semantics, which compares some mathematical objects in a natural way to programs and language constructs (for example, relations in a program are treated as relations on a set of terms, conjunction is the intersection of relations, etc.). The standard way to set such semantics is known as the smallest Herbrand model, and for miniKanren, this has already been done before (also in our laboratory).
After this, the completeness of the search in the language, and at the same time the correctness, can be formulated as the equivalence of these two semantics - the coincidence of the sets of answers for a particular program in them. We managed to prove it. It is interesting (and a little sad) that we did without co-induction, using several nested inductions with different parameters.
As a consequence, we also get the correctness of some useful language transformations (in terms of the set of solutions obtained): if the transformation obviously does not change the corresponding mathematical object, for example, reordering conjuncts or using distributivity of conjunction or disjunction, then the search results do not change.
Now we want to use semantics for evidence of other useful properties of the language, for example, criteria for completeness / divergence or correctness of additional language constructs.
We also took a more detailed and rigorous description of our formalization with the help of Coq. Having overcome many different difficulties and invested a lot of strength, we were able at the moment to define the operational semantics of the language and to carry out several proofs that on a piece of paper were “Obvious. Qed. We do not lose faith in ourselves.
Today I will talk about my research in the field of relational programming, which I do at the university and as a student-researcher in the laboratory of language tools JetBrains Research.
What is relational programming? Usually we run the function with arguments and get the result. And in the relational case, you can do the opposite: fix the result and one argument, and get the second argument. The main thing is to write the code correctly and have patience or a good cluster.
')

About myself
My name is Dmitry Rozplokhas, I am a first-year postgraduate student at the St. Petersburg Higher School, and last year I graduated from the Bachelor of Academic University with a degree in Programming Languages. From the third year of a bachelor degree I am also a research student in the laboratory of language tools JetBrains Research.
Relational programming
General facts
Relational programming is when instead of functions you describe the relationship between the arguments and the result. If the language for this is sharpened, you can get certain bonuses, for example, the ability to run a function in the opposite direction (by the result, restore the possible values of the arguments).
In general, this can be done in any logical language, but interest in relational programming arose simultaneously with the appearance of the minimalistic pure logical language miniKanren about ten years ago, which made it possible to conveniently describe and use similar relationships.
Here are some of the most advanced examples of use: you can write a proof checker and use it to search for evidence ( Near et al., 2008 ) or create an interpreter of a language and use it to generate test suite programs ( Byrd et al., 2017 ).
Syntax and toy example
miniKanren is a small language; only basic mathematical constructions are used to describe relationships. This is an embeddable language, its primitives are a library for some external language, and small programs on miniKanren can be used inside programs in another language.
External languages suitable for miniKanren, a whole bunch. Originally, it was Scheme, we work with the version for Ocaml ( OCanren ), and the full list can be viewed at minikanren.org . Examples in this article will also be on OCanren. Many implementations add helper functions, but we will focus only on the core language.
Let's start with the data types. Conventionally, they can be divided into two types:
- Constants are some data from the language in which we are embedded. Lines, numbers, even arrays. But for the base miniKanren, this is all a black box, constants can only be checked for equality.
- "Therm" is a tuple of several elements. Usually used in the same way as data constructors in Haskell: data constructor (string) plus zero or more parameters. OCanren uses the usual data constructors from OCaml.
For example, if we want to work with arrays in miniKanren itself, then it should be described in terms of terms, by analogy with functional languages - as a simply linked list. A list is either an empty list (denoted by some simple term), or a pair from the first element of the list (“head”) and the rest of the elements (“tail”).
let emptyList = Nil let list_123 = Cons (1, Cons (2, Cons (3, Nil))) The program in the language miniKanren is the ratio between some variables. When you start the program gives all possible values of variables in general. Often, implementations allow you to limit the number of answers in the output, for example, to find only the first — the search does not always stop after finding all the solutions.
You can write several relations, which are defined through each other and even called recursively, as functions. For example, below, instead of the function define the relationship : list is a concatenation of lists and . Functions that return relationships traditionally end with an “o” to distinguish them from ordinary functions.
The relationship is recorded as some statement regarding its arguments. We have four basic operations :
- Unification or equality (===) of two terms, terms may include variables. For example, you can write the relationship "list consists of one element ":
let isSingletono xl = l === Cons (x, Nil) - Conjunction (logical "and") and disjunction (logical "or") - as in ordinary logic. In OCanren, denoted as &&& and |||. But in principle there is no logical negation in MiniKanren.
- Adding new variables. In logic, it is a quantifier of existence. For example, to check a list for nonempty, you need to check that the list consists of a head and a tail. They are not arguments of the relationship, so you need to create new variables:
let nonEmptyo l = fresh (ht) (l === Cons (h, t))
An attitude can call itself recursively. For example, the “element is on the list. ” We will solve this problem through the analysis of trivial cases, as in functional languages:
- Either the list head is equal
- Or lies in the tail
let membero lx = fresh (ht) ( (l === Cons (h, t)) &&& (x === h ||| membero tx) ) The basic version of the language is based on these four operations. There are also extensions that allow other operations to be used. The most useful of them is the disequality constraint for specifying the inequality of two terms (= / =).
Despite its minimalism, miniKanren is quite an expressive language. Here, for example, looks like the relational concatenation of two lists. The function of the two arguments turns into a triple relation " is a concatenation of lists and ".
let appendo ab ab = (a === Nil &&& ab === b) ||| (fresh (ht tb) (* : fresh &&& *) (a = Cons (h, t)) (appendo tb tb) (ab === Cons (h, tb))) The solution is not structurally different from how we would write it in a functional language. We parse two cases combined by a disjunction:
- If the first list is empty, then the second list and the result of concatenation are equal.
- If the first list is not empty, then we parse it on the head and tail and construct the result using a recursive call of the relationship.
We can make a request to this relation, fixing the first and second argument - we get the concatenation of lists:
run 1 (λ q -> appendo (Cons (1, Cons (2, Nil))) (Cons (3, Cons (4, Nil))) q) ⇒
q = Cons (1, Cons (2, Cons (3, Cons (4, Nil)))) We can fix the last argument - we get all the breaks in this list into two.
run 4 (λ qr -> appendo qr (Cons (1, Cons (2, Cons (3, Nil))))) ⇒
q = Nil, r = Cons (1, Cons (2, Cons (3, Nil))) | q = Cons (1, Nil), r = Cons (2, Cons (3, Nil)) | q = Cons (1, Cons (2, Nil)), r = Cons (3, Nil) | q = Cons (1, Cons (2, Cons (3, Nil))), r = Nil Anything else is possible. A slightly more non-standard example in which we fix only part of the arguments:
run 1 (λ qr -> appendo (Cons (1, Cons (q, Nil))) r (Cons (1, Cons (2, Cons (3, Cons (4, Nil)))))) ⇒
q = 2, r = Cons (3, Cons (4, Nil)) How it works
From the point of view of the theory, there is nothing impressive here: you can always simply run through all possible options for all arguments, checking for each set whether they behave with respect to a given function / relationship as we would like (see “British Museum Algorithm” ) . It is interesting that here the search (in other words, the search for a solution) uses exclusively the structure of the described relation, due to which it can be relatively effective in practice.
The search goes against accumulating information about various variables in the current state. We either know nothing about each variable, or we know how it is expressed in terms of terms, values, and other variables. For example:
b = Cons (x, y)
c = Cons (10, z)
x = ?
y = ?
z = ?
Going through unification, we look at two terms with this information in mind and either update the state or stop searching if two terms cannot be unified. For example, having executed unification b = c, we will receive new information: x = 10, y = z. But the unification b = Nil will cause a contradiction.
We perform a search in conjunctions sequentially (so that information accumulates), and in a disjunction we divide the search into two parallel branches and move on, alternating steps in them - this is the so-called interleaving search. Thanks to this alternation, the search is complete - every suitable solution will be found in a finite time. For example, in the Prolog language this is not the case. Something like a depth traversal (which may hang on an endless branch) is performed there, and the interleaving search is essentially a tricky modification of the width traversal.
Let's now see how the first request from the previous section works. Since appendo has recursive calls, we will add indices to variables to distinguish them. The figure below shows the search tree. The arrows indicate the direction of information dissemination (except for the return from recursion). Between disjunctions, information is not distributed, but between conjunctions it spreads from left to right.

- We start with an external call to appendo. The left branch of the disjunction dies due to contradiction: the list not empty
- Auxiliary variables are entered in the right branch, which are then used to “parse” the list. on the head and tail.
- After this, a recursive call to appendo for a = [2], b = [3, 4], ab =? Occurs, in which similar operations take place.
- But in the third call to appendo, we already have a = [], b = [3,4], ab = ?, and then the left disjunction just works, after which we get the information ab = b. But in the right branch there is a contradiction.
- Now we can write out all the available information and restore the answer by substituting the values of the variables:
a_1 = [1, 2]
b_1 = [3, 4]
ab_1 = Cons h_1 tb_1
h_1 = 1
a_2 = t_1 = [2]
b_2 = b_1 = [3, 4]
ab_2 = tb_1 = Cons h_2 tb_2
h_2 = 2
a_3 = t_2 = Nil
b_3 = b_2 = b_1 = [3, 4]
ab_3 = tb_2 = b_3 = [3, 4] - It follows that = Cons (1, Cons (2, [3, 4])) = [1, 2, 3, 4], as required.
What did I do in undergraduate
Everything slows down
As always: they promise you that everything will be super declarative, but in fact you need to adapt to the language and write everything in a special way (keeping in mind how everything will be executed) so that at least something other than the simplest examples will work. It is disappointing.
One of the first problems that a novice miniKanren programmer faces is that everything depends very much on the order in which you describe the conditions (conjuncts) in the program. With one order, everything is OK, but they changed two conjuncts in places and everything began to work very slowly or not at all. This was unexpected.
Even in the example with appendo, the launch in the opposite direction (the generation of the list splits into two) does not end unless you explicitly indicate how many answers you want (then the search will be terminated after the required number has been found).
Suppose we fix the source variables like this: a =?, B =?, Ab = [1, 2, 3] (see figure below) In the second branch, in a recursive call, this information will not be used in any way (the variable ab and restrictions on and appear only after this call). Therefore, the first recursive call, all its arguments will be free variables. This call will generate all sorts of triples from two lists and their concatenation (and this generation will never end), and then among them will be selected those for which the third element has turned out exactly the way we need.

Everything is not as bad as it may seem at first glance, because we will sort out these triples in large groups. Lists with the same length, but different elements, are in no way different from the point of view of the function, therefore they will fall into one solution - in place of the elements will be free variables. Nevertheless, we will still sort out all possible lengths of the lists, although we only need one, and we know which one. This is a very irrational use (non-use) of information when searching.
This particular example is easy to fix: you just need to transfer the recursive call to the end and everything will work as it should. Before the recursive call, there will be a unification with the variable ab and a recursive call will be made from the tail of this list (as a normal recursive function). This definition with a recursive call at the end will work well in all directions: for a recursive call we manage to accumulate all possible information about the arguments.
However, in any slightly more complicated example, when there are several meaningful challenges, there is no one specific order for which everything will be fine. The simplest example: expanding a list using concatenation. We fix the first argument - this is the order we need, we fix the second - we need to swap calls. Otherwise, it is searched for a long time and the search does not end.
reverso x xr = (x === Nil &&& xr == Nil) ||| (fresh (ht tr) (x === Cons (h, t)) (reverso t tr) (appendo tr (Cons (h, Nil)) xr)) This happens because interleaving search processes the conjuncts consistently, and how to do it differently, without losing the acceptable efficiency, no one could think of it, although they tried. Of course, all the solutions will someday be found, but with the wrong order, they will be searched for so unrealistically long that there is no practical sense in this.
There are techniques for writing programs to avoid this problem. But many of them require special skill and imagination to use, and the result is very large programs. An example is the term size bounding technique and the definition of binary division with the remainder through multiplication with its help. Instead of stupidly writing a mathematical definition
divo nmqr = (fresh (mq) (multo mq mq) (pluso mq rn) (lto rm)) I have to write a recursive definition for 20 lines + a large auxiliary function that cannot be read (I still do not understand what is being done there). It can be found in Will Byrd’s dissertation in the Pure Binary Arithmetic section.
In view of the foregoing, I want to come up with some sort of search modification so that simply and naturally written programs also work.
We optimize
We noticed that when everything is bad, the search will not be completed unless you explicitly indicate the number of answers and do not interrupt it. Therefore, we decided to fight precisely with the incompleteness of the search - it is much easier to concretize than “it takes a long time”. In general, of course, I just want to speed up the search, but it is much more difficult to formalize, so we started with a less ambitious task.
In most cases, when the search diverges, a situation occurs that is easy to track. If some function is called recursively, and when we call the argument recursively, we have the same or less specific arguments, then in the recursive call another such subtask is generated again and endless recursion occurs. Formally, it sounds like this: there is a substitution, applying it to the new arguments, we get the old ones. For example, in the figure below, a recursive call is a generalization of the original: you can substitute = [x, 3], = x and get the original call.

It can be traced that such a situation happens in the examples of divergence we have already encountered. As I wrote earlier, when appendo is started in the opposite direction, a recursive call will be made with free variables instead of all variables, which, of course, is less specific than the original call, in which the third argument was fixed.
If we run reverso with arguments x =? and xr = [1, 2, 3], then it can be traced that the first recursive call will again occur with two free variables, so the new arguments can again be translated into previous ones in an obvious way.
reverso x x_r (* x = ?, x_r = [1, 2, 3] *) fresh (ht t_r) (x === Cons (h, t)) (* x_r = [1, 2, 3] = Cons 1 (Cons 2 (Cons 3 Nil))) x = Cons (h, t) *) (reverso t t_r) (* : t=x, t_r=[1,2,3], *) Using this criterion, we can detect the divergence in the process of program execution, understand that everything is bad with this order, and dynamically change it to another one. Due to this, ideally, for each call just the necessary order will be selected.
You can do this naively: if there is a divergence in the conjunct, then we hammer on all the answers that he has already found and postpone his execution for later, “skipping ahead” the next conjunct. Then, perhaps, when we will execute it further, more information will be known already and there will be no divergence. In our examples, this will lead to exactly the desired swap of the conjuncts.
There are less naive ways that allow, for example, not to lose the work already done, postponing execution. Already with the most blunt variant of changing the order, the divergence disappeared in all simple examples suffering from conjunction noncommutativity, which we know, including:
- sorting the list of numbers (it is the generation of all permutations of the list),
- Peano arithmetic and binary arithmetic,
- generation of binary trees of a given size.
This turned out to be an unexpected surprise for us. In addition to divergence, optimization also struggles with the inhibition of programs. The diagrams below show the execution time of programs with two different orders in conjunctions (relatively speaking, one very good and one of many bad ones). It was launched on a computer with an Intel Core i7 CPU M 620, 2.67GHz x 4, 8GB RAM configuration with Ubuntu 16.04 operating system.
When the order is optimal (we pick it up with our hands), optimization slows down the execution a bit, but is not critical

But when the order is not optimal (for example, suitable only for launching in the other direction), with optimization it turns out much faster. Crosses mean that we just could not wait for the end, it works much longer

How to break nothing
All this was based purely on intuition and we wanted to prove it strictly. The theory is all the same.
In order to prove something, we need the formal semantics of the language. We described the operational semantics for miniKanren. This is a simplified and mathematical version of the real implementation of the language. It uses a very limited (therefore, easy to use) version in which you can specify only the terminating execution of programs (the search must be finite). But for our purposes, this is exactly what is needed.
To prove the criterion, a lemma is first formulated: the execution of a program from a more general state will work longer. Formally: the output tree in semantics has a great height. This is proved by induction, but we must very carefully generalize the statement, otherwise the inductive hypothesis will not be strong enough. It follows from this lemma that if during the execution of the program the criterion worked, then the output tree has its own subtree greater or equal in height. This is a contradiction, since for inductively defined semantics all trees are finite. This means that in our semantics the execution of this program is inexpressible, which means that the search in it does not end.
The proposed method is conservative: we change something only when we are convinced that everything is already very bad and impossible to do, therefore we do not break anything in terms of the completeness of the programs.
The main evidence contains quite a lot of details, so we had the desire to formally verify it by writing to Coq . However, it turned out to be quite difficult technically, so we cooled our ardor and seriously engaged in automatic verification only in the magistracy.
Publication
In the middle of the paper, we presented this study at the ICFP-2017 poster session at the Student Research Competition . There we met the creators of the language, Will Byrd and Daniel Friedman, and they said it was meaningful and we need to look at it in more detail. By the way, Will is generally friends with our laboratory at JetBrains Research. All miniKanren research began with us when, in 2015, Will held a summer school on relational programming in St. Petersburg.
A year later, we brought our work to a more or less complete form and presented an article at the Conference Principles and Practice of Declarative Programming 2018.
What i do in master
We wanted to continue to engage in formal semantics for miniKanren and rigorous evidence of all its properties. In the literature, usually properties (often far from obvious) are simply postulated and demonstrated by examples, but no one proves anything. For example, the main book on relational programming is a list of questions and answers, each of which is devoted to a particular piece of code. Even for the statement about the completeness of interleaving search (and this is one of the most important advantages of miniKanren over a standard Prolog), it is impossible to find a rigorous formulation. We cannot live like this, we decided, and, having received a blessing from Will, set to work.
Let me remind you that the semantics developed by us at the previous stage had a significant limitation: only programs with a finite search were described. In miniKanren, incomplete programs are also of interest, because they can list an infinite number of answers. Therefore, we needed steeper semantics.
There are many different standard ways of defining the semantics of a programming language; we only needed to choose one of them and adapt it to a specific case. We described the semantics as a labeled transition system — a set of possible states in the search process and transitions between these states, some of which are marked with, which means that at this stage of the search there was another answer. The execution of a particular program is thus determined by the sequence of such transitions. These sequences can be finite (coming to a terminal state) or infinite, describing simultaneously terminating and incomplete programs. In order to strictly mathematically set such an object, you need to use a co-inductive definition.
The semantics described above is operational - it reflects the real implementation of the search. In addition to it, we also use denotational semantics, which compares some mathematical objects in a natural way to programs and language constructs (for example, relations in a program are treated as relations on a set of terms, conjunction is the intersection of relations, etc.). The standard way to set such semantics is known as the smallest Herbrand model, and for miniKanren, this has already been done before (also in our laboratory).
After this, the completeness of the search in the language, and at the same time the correctness, can be formulated as the equivalence of these two semantics - the coincidence of the sets of answers for a particular program in them. We managed to prove it. It is interesting (and a little sad) that we did without co-induction, using several nested inductions with different parameters.
As a consequence, we also get the correctness of some useful language transformations (in terms of the set of solutions obtained): if the transformation obviously does not change the corresponding mathematical object, for example, reordering conjuncts or using distributivity of conjunction or disjunction, then the search results do not change.
Now we want to use semantics for evidence of other useful properties of the language, for example, criteria for completeness / divergence or correctness of additional language constructs.
We also took a more detailed and rigorous description of our formalization with the help of Coq. Having overcome many different difficulties and invested a lot of strength, we were able at the moment to define the operational semantics of the language and to carry out several proofs that on a piece of paper were “Obvious. Qed. We do not lose faith in ourselves.
Source: https://habr.com/ru/post/441114/
All Articles