Hey, full steaks, let's practice skills. I propose to knead the gyrus, it seems to me that it is interesting to do it using a different, unusual, paradigm. Most developers have an advanced algorithmization skill - the task turns into building blocks that need to be connected, to think over a sequence of moves that leads to the desired conclusion.

Here, a week ago, the Prologue was mentioned, I would like to reply that the Prolog language is suitable for solving problems. I have already touched on this topic, and cited several solutions of random problems from the site with tasks for algorithms that are available to me, I would like to show that any complex solution is available in a declarative language, and it can work no slower (well, maybe, noticeably not very slower).

I couldn’t take the next task for a long time, and now I’ve got the first solution, showing the problem and finding out how much slow it is.

The prologue is interesting in that you can create a deductive program that shows a lot of solutions and can even limit it, but does not provide a way to iterate,
the algorithm will be developed solver an interpreter.

So, the problem is this :

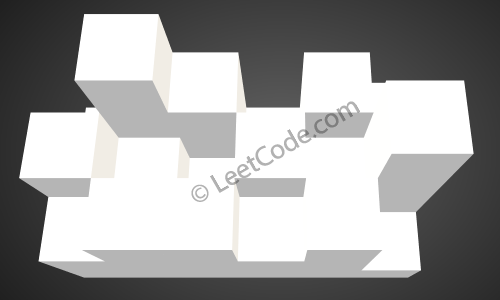
1. Trapping Rain Water II
   If you are looking at the bottom of the cell line, you can see the trap after raining.
   Note:
   Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.
   Example:
   
   
   
   Given the following 3x6 height map:
   [
   [1,4,3,1,3,2],
   [3,2,1,3,2,4],
   [2,3,3,2,3,1]
   ]
   Return 4.

After lengthy attempts to formulate a solution, I came to the following formulation:
It is necessary to pour a maximum of water into each cell, which would not pour out of it . I propose to pour into each cell, some amount of water, but so that it is less equal to the maximum value of all possible.

It turned out like this:

reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!. 

this predicate takes an input list (matrix), and turns it into a solution, into a matrix in which there are other values ​​that will be a valid answer. Then another predicate will take these two lists element by element and find the total sum.

 repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X). 

this predicate will take one of the solutions, and check whether it is “normal” if it satisfies the condition of the problem, then this is the solution.

This is the "generate and test" method, we say that the value is in such and such a set and we review all the elements of this set, checking some output condition.

This means that the predicate puts (Vals, X0, X1) will receive a new solution, here in the first place there is a list of all possible values ​​of heights that are in this matrix, the possible values ​​of heights for each cell will be selected from it. By analyzing the input tests, it was found that in this task you can fill the entire cell, if you can insert so much water around it that it pours with the head.

Overall, this predicate looks more complicated, it is necessary to process triples of lines that make up one 3x3 square (yes, there is no array in Prolog, but the description of the input data looks like this, so we use this, in declarative programming you may not know about the indexes of the elements in the array , there is only a list with his head and tail, so we simply describe such a template that corresponds to the input specification).

 puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St). 

This is how it turns out to express a detour of the matrix from which you can take the first three (and further) lines from which, you can also select, from left to right, triples of elements, and now between the eight neighbors there will be one [Ita] [This] landscape cell. With sel_biger (R2, V, R21) a new value of this cell is made.

This value can be set to the current cell, it can be one of the possible heights, and even a list of them sorted in descending order, so that the first one will be the greatest height available at all, and then any one after it:

 sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X). 

It was a description of the "decision generator", and then we need to make sure that the matrix is ​​received, from whatever heights filled in at each point, is similar to the answer required from us.

And it was necessary to find such a state that the water would settle in the holes, I will try to put it like this:
of the nine values ​​of the three by three square, the center should always be such a height that it does not contradict the input map so that the change in the balance that was originally in these cells did not work, if there was a height, then the cells should not remain above it, even if everything will flood with water, then we can say that a high cell should remain itself or be replaced by a higher value, but such that it is equal to all neighbors, i.e. the cells on the left-right and above-below from the current should exceed or be equal, if there is more water in the cell, then only if it has risen around ...

 %%   balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). %%     ,    33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). %%    , %        equ(_,[],_,[]):-!. equ(C,_,C,_):-!. equ(C0,_,C,N):-C>C0,!,findall(X,(member(X,N),X<C),[]). equ(C0,[C0|T0],C,[C|T]):-!,equ(C0,T0,C,T). 

And the final two predicates, which take the input matrix, start searching for a suitable result, subtract the sum of the elements among themselves, and find the final amount that was required in the problem:

 diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. %%  ,      sums(X,S):-reptest(X,X1),diffall(X,X1,S). 

I will demonstrate the tests that provided the site .

 reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!. repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X). puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St). sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X). %   balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). %     ,    33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). %    , %        equ(_,[],_,[]):-!. equ(C,_,C,_):-!. equ(C0,_,C,N):-C>C0,!,findall(X,(member(X,N),X<C),[]). equ(C0,[C0|T0],C,[C|T]):-!,equ(C0,T0,C,T). diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. sums(X,S):-reptest(X,X1),diffall(X,X1,S). %unit-tests framework assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp). :-assert_are_equal(sums([[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[1,3,3,1,3,2],[3,2,1,3,2,3],[3,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[12,13,1,12],[13,4,13,12],[13,8,10,12],[12,13,12,12],[13,13,13,13]],14),true). :-assert_are_equal(sums([[2,3,4],[5,6,7],[8,9,10],[11,12,13],[14,15,16]],0),true). :-assert_are_equal(sums([],0),true). :-assert_are_equal(sums([[1]],0),true). :-assert_are_equal(sums([[2,3]],0),true). :-assert_are_equal(sums([[3],[2]],0),true). :-assert_are_equal(sums([[18,2,3],[4,5,6],[7,8,9]],0),true). :-assert_are_equal(sums([[3,5,5],[5,4,5],[5,5,5]],1),true). :-assert_are_equal(sums([[5,5,5,1],[5,1,1,5],[5,1,5,5],[5,2,5,8]],3),true). :-assert_are_equal(sums([[2,2,2],[2,1,2],[2,1,2],[2,1,2]],0),true). :-assert_are_equal(sums([[17,2,3,4,5,6,7,8,9,10]],0),true). :-assert_are_equal(sums([[9,9,9,9,9],[9,2,1,2,9],[9,2,8,2,9],[9,2,3,2,9],[9,9,9,9,9]],57),true). %:-assert_are_equal(sums([[9,9,9,9,9,9,8,9,9,9,9],[9,0,0,0,0,0,1,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,9,9,9,9,9,9,9,9,9,9]],215),true). :-assert_are_equal(sums([[11,21,31],[81,9,41],[17,61,51]],12),true). :-assert_are_equal(sums([[3,3,4,4,4,2],[3,1,3,2,1,4],[7,3,1,6,4,1]],5),true). %:-assert_are_equal(sums([[78,16,94,36],[87,93,50,22],[63,28,91,60],[64,27,41,27],[73,37,12,69],[68,30,83,31],[63,24,68,36]],44),true). 

I had to comment on the tests. not everyone passed.

The challenge, how to speed it up?

Part of the solutions is not to be, because of the long search of solutions, it is too slow to generate them in this order, here the complexity is probably n !, all possible values ​​for each cell of the array are sorted.

It is convenient to express this task in the programming system in constraints, just on the Prologue this is called: CLP (FD): Constraint Logic Programming over Finite Domains.

clp (fd) SWI-Prolog distribution. The variables need to be set.
')
>>

I will formulate the problem like this:
We need such a list, each element of which of the set of values ​​is more or equal to it and the maximum value over the entire map, taking into account the restriction that the elements must be arranged clearly in the order of the corresponding spilled liquid.

This is how I make from the input list, a new list, the elements of which have become unknown in the specified range (from the R2 value of the current element and up to the Maximum value V)
At the entrance there is a list of lists, at the exit a new list with the maximum distribution of values,
that satisfy balns fluid balance limits:

 checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St). 

This is both a generator and simultaneously a check, it is indicated that the elements are in such a set, and then gradually imposing a check the narrowing of this set occurs. Further, something remains, and it can be "marked", i.e. arrange integer values ​​that will satisfy the sum of all constraints. Calling labeling ([down], FX2) causes to fill (connect) variable unknown with specific values, and there may be several such options, but we always take the very first one, since it was said that all variables move down in the search, from their upper bounds, these are the search options [down].

Now, in fact, what is "balanced" is when poured water does not overflow from cell to cell. This is the correspondence of the initial ordering of elements One may think that filling the cells will retain the shape of the original landscape, this means if there was a wall, then it can be covered with water on top, so that it becomes necessarily equal to all its neighbors, or if it is not a wall covered with water ...

Consider the balance of situations:
-If the cell is flooded, then next to the same or even higher (all of a sudden it is the wall).
-If the cell was equal to the next, then it must be equal to the new and next.
- And in the extreme case, the cell did not change its meaning, and still, what were its neighbors:

 %   balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). %     ,    33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). %    , %        equ(C0,_,C,[U,L,R,D]):-C#>C0,C#=<U,C#=<R,C#=<L,C#=<D. equ(_,[],_,[]). equ(C0,[C0|T0],C,[C|T]):-equ(C0,T0,C,T). equ(C,_,C1,_):-C1#=C. 

This is how you can transfer your attitude to the task into the program. I don’t need to think about the solution algorithm; it’s important to provide a correct description of the result, to set correctly all the initial constraints (sets of values). This approach can simply be "mixed" with the usual search with return and recursion inherent in Prolog. This is a way to formulate even more declarative programs than using the classical methods of Prolog.

I will give the resulting solution, with a set of tests:

 :- use_module(library(clpfd)). checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St). %   balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). %     ,    33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). %    , %        equ(C0,_,C,[U,L,R,D]):-C#>C0,C#=<U,C#=<R,C#=<L,C#=<D. equ(_,[],_,[]). equ(C0,[C0|T0],C,[C|T]):-equ(C0,T0,C,T). equ(C,_,C1,_):-C1#=C. diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. sums(X,S):-checks(X,X1),!,diffall(X,X1,S). %unit-tests framework assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp). :-assert_are_equal(sums([[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[1,3,3,1,3,2],[3,2,1,3,2,3],[3,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[12,13,1,12],[13,4,13,12],[13,8,10,12],[12,13,12,12],[13,13,13,13]],14),true). :-assert_are_equal(sums([[2,3,4],[5,6,7],[8,9,10],[11,12,13],[14,15,16]],0),true). :-assert_are_equal(sums([[18,2,3],[4,5,6],[7,8,9]],0),true). :-assert_are_equal(sums([[3,5,5],[5,4,5],[5,5,5]],1),true). :-assert_are_equal(sums([[5,5,5,1],[5,1,1,5],[5,1,5,5],[5,2,5,8]],3),true). :-assert_are_equal(sums([[2,2,2],[2,1,2],[2,1,2],[2,1,2]],0),true). :-assert_are_equal(sums([[17,2,3,4,5,6,7,8,9,10]],0),true). :-assert_are_equal(sums([[9,9,9,9,9],[9,2,1,2,9],[9,2,8,2,9],[9,2,3,2,9],[9,9,9,9,9]],57),true). :-assert_are_equal(sums([[78,16,94,36],[87,93,50,22],[63,28,91,60],[64,27,41,27],[73,37,12,69],[68,30,83,31],[63,24,68,36]],44),true). :-assert_are_equal(sums([[11,21,31],[81,9,41],[17,61,51]],12),true). :-assert_are_equal(sums([[5,5,5],[5,1,5],[5,5,5]],4),true). :-assert_are_equal(sums([[5,5,5],[5,1,5],[5,1000,6]],4),true). :-assert_are_equal(sums([[5,8,7,7],[5,2,1,5],[7,1,7,1],[8,9,6,9],[9,8,9,9]],12),true). :-assert_are_equal(sums([[11,21,31],[81,9,41],[17,61,51]],12),true). :-assert_are_equal(sums([[3,3,4,4,4,2],[3,1,3,2,1,4],[7,3,1,6,4,1]],5),true). :-assert_are_equal(sums([[14,17,18,16,14,16],[17,3,10,2,3,8],[11,10,4,7,1,7],[13,7,2,9,8,10],[13,1,3,4,8,6],[20,3,3,9,10,8]],25),true). :-assert_are_equal(sums([[14,17,12,13,20,14],[12,10,5,8,9,5],[16,1,4,7,2,1],[17,4,3,1,7,2],[16,6,5,8,7,6],[17,10,4,8,5,6]],12),true). 

 :-assert_are_equal(sums([[13,16,15,18,15,15],[14,1,8,9,7,9],[19,5,4,2,5,10],[13,1,7,9,10,3],[17,7,5,10,6,1],[15,9,8,2,8,3]],36),true). :-assert_are_equal(sums([[18,13,13,17,12,11],[17,2,6,10,5,10],[11,10,2,8,8,2],[12,6,10,8,8,7],[18,4,7,6,7,4],[20,5,9,2,3,10]],18),true). :-assert_are_equal(sums([[14,20,11,19,19,16],[11,10,7,4,9,6],[17,2,2,6,10,9],[15,9,2,1,4,1],[15,5,5,5,8,7],[14,2,8,6,10,7]],11),true). :-assert_are_equal(sums([[19383,10886,12777,16915,17793,18335,15386,10492,16649,11421],[12362,27,8690,59,7763,3926,540,3426,9172,5736],[15211,5368,2567,6429,5782,1530,2862,5123,4067,3135],[13929,9802,4022,3058,3069,8167,1393,8456,5011,8042],[16229,7373,4421,4919,3784,8537,5198,4324,8315,4370],[16413,3526,6091,8980,9956,1873,6862,9170,6996,7281],[12305,925,7084,6327,336,6505,846,1729,1313,5857],[16124,3895,9582,545,8814,3367,5434,364,4043,3750],[11087,6808,7276,7178,5788,3584,5403,2651,2754,2399],[19932,5060,9676,3368,7739,12,6226,8586,8094,7539]],79058),true). :-assert_are_equal(sums([[10795,10570,11434,10378,17467,16601,10097,12902,13317,10492],[16652,756,7301,280,4286,9441,3865,9689,8444,6619],[18440,4729,8031,8117,8097,5771,4481,675,709,8927],[14567,7856,9497,2353,4586,6965,5306,4683,6219,8624],[11528,2871,5732,8829,9503,19,8270,3368,9708,6715],[16340,8149,7796,723,2618,2245,2846,3451,2921,3555],[12379,7488,7764,8228,9841,2350,5193,1500,7034,7764],[10124,4914,6987,5856,3743,6491,2227,8365,9859,1936],[11432,2551,6437,9228,3275,5407,1474,6121,8858,4395],[16029,1237,8235,3793,5818,4428,6143,1011,5928,9529]],68900),true). :-assert_are_equal(sums([[18776,12404,14443,15763,14613,14538,18606,16840,12904,14818],[15128,688,7369,7917,9917,6996,3324,7743,9470,2183],[18490,5499,9772,6725,5644,5590,7505,8139,2954,9786],[17669,8082,8542,8464,197,9507,9355,8804,6348,8611],[13622,7828,9299,7343,5746,5568,4340,5422,3311,3810],[17605,1801,5661,3730,4878,1305,9320,8736,9444,8626],[18522,3465,6708,3416,8282,3258,2924,7637,2062,5624],[12600,2036,3452,1899,9379,5550,7468,71,973,7131],[13881,4930,8933,5894,8660,163,7199,7981,8899,2996],[12959,3773,2813,9668,7190,1095,2926,6466,5084,1340]],61413),true). :-assert_are_equal(sums([[12090,17684,13376,15542,15936,19107,17445,19756,19179,18418],[16887,9412,3348,2172,1659,2009,2336,5210,6342,7587],[18206,9301,7713,7372,5321,1255,4819,4599,7721,9904],[15939,9811,3940,5667,1705,6228,1127,9150,5984,6658],[13920,9224,2422,7269,1396,4081,5630,84,9292,1972],[17672,3850,7625,5385,1222,9299,6640,6042,3898,713],[12298,6190,524,2590,8209,8581,8819,9336,7732,1155],[15994,8004,379,4769,5273,1776,8850,7255,1860,8142],[15579,5884,1993,3205,7621,9567,2504,613,1961,2754],[11326,4259,8944,8202,3202,3506,6784,2021,2842,868]],89383),true). :-assert_are_equal(sums([[19528,15189,18872,19908,19958,10498,18036,18808,17753,16248],[13303,3333,2133,1648,2890,9754,7567,1746,368,9529],[14500,8046,3788,9797,6249,6990,3303,3033,5363,2497],[10253,4892,7686,9125,1152,3996,5975,9188,9157,3729],[15436,2460,3414,3921,460,6304,28,8027,8050,6748],[17556,8902,4794,7697,8699,1043,1039,2002,428,6403],[14500,681,7647,8538,6159,5151,2535,2134,4339,1692],[12215,6127,504,5629,49,964,8285,6429,5343,6335],[13177,2900,5238,7971,6949,289,5367,7988,2292,5795],[10743,3144,2829,8390,1682,5340,3541,569,3826,4232]],100439),true). 

These were tests from the site, only the first 30 pieces. The result is excellent, the problem is solved, and even quickly, all the times up to one second.

You can check ...

As a conclusion

Declarative programming involves detailed formalization of the problem, and the solver will look for the most efficient solution that satisfies the conditions.

A little going into the topic, you can open minizinc , a programming language in which only this paradigm is inherent. Formulated a set of values, indicated restrictions, and voila, the answer. They solve sudoku , map coloring tasks, drawing up work plans , resource problems, scheduling. I propose to train ...