HL 2018. Abstract of the report “Make passwords great again! How to defeat brute force and leave hackers with nothing

Hi, Habr! My name is Ahmadeev Rinat, I Sr. PHP developer.
I present to you the summary of the report Make passwords great again! How to defeat brute force and leave hackers with nothing from Alexei Yarmishkin from Virgil Security with HighLoad ++ 2018 .
When I went to the report, I was pessimistic. But since this is Virgil Security, then I decided to go. At the beginning, the report seemed to be really captain, and I even began to lose interest, but then, as it turned out, I even learned several new approaches to protecting passwords that are different from regular hashing with salt.
The report discusses ways to protect passwords ranging from hashes to more modern approaches, such as Facebook's password Onion, Sphinx and Pythia. At the very end is a new Simple Password-Hardened Encryption Services (PHE).
I liked the report so much that I prepared a summary. I recommend everyone to read.
Alexey Ermishkin shared slides and video of the report in the comments:
Abstract
Introduction

Hello everyone, good morning everyone! I am glad to see you all at the Highload conference. My name is Alexey Ermishkin, I work for Virgil Security.

We develop various cryptographic products for both individual developers and businesses. Focusing on end-to-end solutions, this is when you do not need to trust the service in order to perform some actions like data transfer, authentication, etc. Our SDKs are open and available for everyone to use.
Long since passwords were used as a means of authentication, as a way to get somewhere. It was a long time before computers appeared. But with the advent of computers, with the advent of IT-systems, people did not abandon the habit of using passwords. This has become a very big problem for developers, because they are faced with the problem of how to make systems both comfortable and fast and protected. Very often, when some two of these aspects are trying to do well, the third is not very good. If you make the system productive and protected, then it can be inconvenient, etc.

So, what are we going to talk about today?
I will talk about protection from offline attacks. When passwords get into your databases, after that the user does not control them. If your database is hacked, it will leak somewhere, then hackers can do anything with it. Even if you somehow protected the passwords, they can start sorting through them and they don’t need to interact with anyone, they already have everything for that. Also, users do not stop using weak passwords. Password policies are certainly a useful thing, but also not always convenient, i.e. when even people enter it seems a strong password, the policy still says you need to add a letter or number, then for them it is not convenient. It is also obvious that the problem is the need to compare what the user entered with what you have in the database. How to do it in a safe manner? Well, let's not forget that inside the company there are also people who are not entirely benevolent and would like to protect themselves from them as well.
Hashes

Basically, why passwords are such a sore subject, why is it worth working with them more carefully? The problem is that the password has a small entropy . What is entropy? This is the amount of information contained in the data, i.e. for example, in the word Highload 8 letters - 8 bytes, but if we count the entropy, it will not be 64 bits like the entire word, but less than 30 bits. When they talk about password cracking today, they say that it is possible to crack passwords with entropy no more there or no less many bits in such and such a time. Those. even the number of passwords is not counted.

How did people start working with password security? The first thing that came to mind is to use unidirectional cryptographic hashes .

Their remarkable feature is that they cannot be turned back. Those. If you transferred some information to this hash, received a value at the output, you cannot get this information back from this value. But, unfortunately, they are very quickly calculated. For example, a modern cluster of 4 NVidia cards can iterate over several billion passwords per second. Those. if the entropy of your password is less than 40 bits, then a cluster of 4 video cards will pick it up there in a minute, or even less.
Rainbow tables

In addition, for every tricky hash there is a rainbow table . What is this table and how are they made?

Those. they take the most popular passwords and combinations of characters that can fit on a hard disk, count hashes for them and put them on some more storage of several terabytes. When a hash is encountered, it can be not calculated, but it can be found very quickly using these tables and compared with a password that was previously calculated. Those. The advantages of tables are that they work very quickly, but you need a lot of space to store them. Nevertheless, there are tables for the most popular hashes on the Internet, you can download them, or even buy them.
Note by the author of the abstract: Wikipedia with the speaker does not agree: "The rainbow table is a special variant of the lookup tables for inverting cryptographic hash functions, using a reasonable compromise mechanism between the table search time and the memory occupied." Those. not the hashes of the most popular passwords that fit on the disk are stored there, but simply the hashes of some passwords, the rest are calculated based on those that exist - there are several passwords per record in the table.
Salt

But again, there is a salt on every rainbow table. What is salt? This is a random set of bytes, which is added to the password. It is stored in a table somewhere near the hash and protects against rainbow tables.

Those. people who have got a base with salted hashes in their hands will still have to calculate these hashes. But the problem is that these hashes are calculated very quickly and the salt does not help much here.
How to slow brute force?

The natural way out of this is to slow down the hashes in some way. How can I do that?

The most naive approach is that we take some kind of hashing function, for example, sha256 and calculate it iteratively, i.e. calculate the hash, from this hash again the hash, etc. You can do this many thousands and even millions of times. The problem is that if you write such an implementation yourself, then it will most likely be slower than the implementation of people who are professionally engaged in brute force passwords.
And so the cryptographers have come up with several functions that are specifically designed to slow down the search for passwords - they use a large amount of memory and all possible modern instructions of the processor. If a password protected by such a function falls into the hands of intruders, then they will have to use very powerful hardware.

For example, the most advanced function of Argon2 works as follows: in the diagram you can see that there are so many different memory blocks that the hash goes through. He does this in various ways back and forth, memory is used very intensively, memory is used all. Optimizing such a function (search speed) is quite difficult.

But these approaches also have their disadvantages. These functions are made specially slow, but they are specially slow, not only for intruders, they will be especially slow for you. They will load your iron. These functions are customizable, i.e. You can choose how much memory will be used to calculate the hash of a single password, up to several gigabytes, how many passes through this memory. If you screw these parameters very seriously, then your own hardware will suffer and if you have a lot of people log in, then you just have to allocate quite substantial resources for password protection and also simple passwords, well, very simple passwords can still be picked up .
Facebook's password Onion

People thought about it and asked whether it was possible to achieve the same properties without loading the backend, without loading their own servers?

One of the pioneers in this was Facebook . These lines, which you see, are the historical stages of Facebook, how they protected passwords, at first they were just passwords, then they took the old function md5 , which was cracked a long time ago, then they added salt to it and took the sha1 hash, and then interesting thing, they carried the calculation of the function hmac (this is a hash with the key) to the remote service.
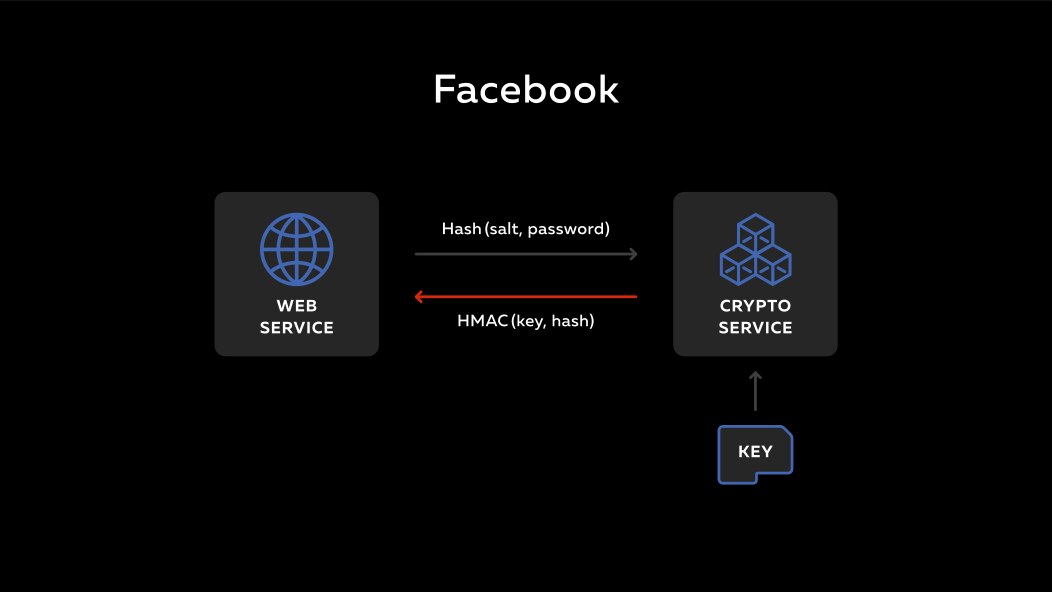
How it works? There is a backend, there is a remote service. There is a secret key on this service. A person enters the backend, enters his password. This password is mixed with salt, which lies in the database, is run through the hash and sent to the service. The service takes its secret key, calculates the hmac function and sends it all back. On the backend it is put into the base.
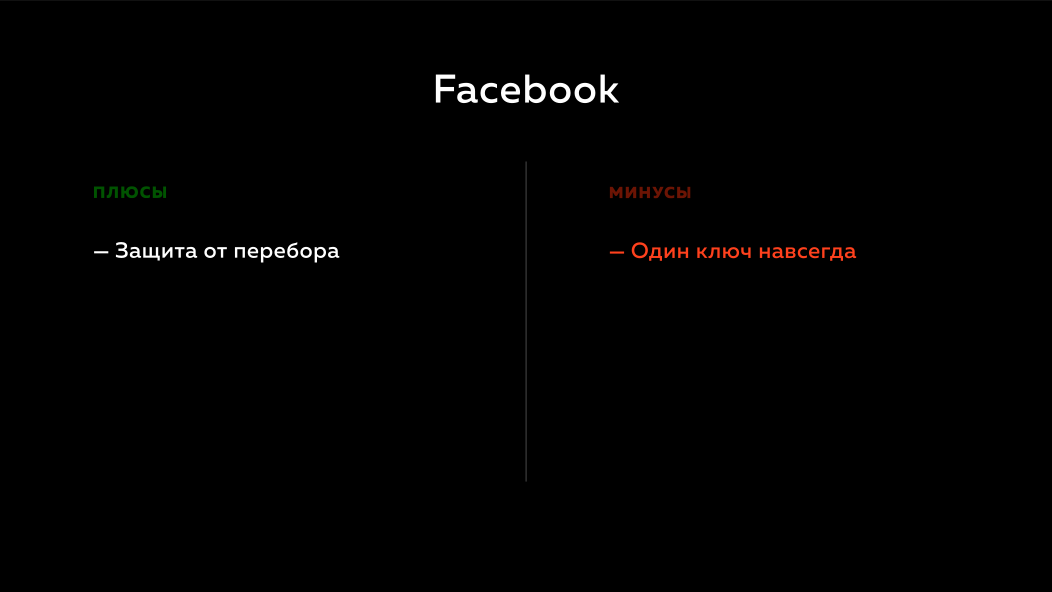
What does this give? If Facebook has a user base, then there is no sense in sorting passwords in it, because they do not have a remote secret key. But the problem with the Facebook approach is that if something happens to their remote secret key, they will be in big trouble. They can't do anything about it, because they use hashes, they use hmac. They have no way to somehow sort out this situation so that the users would not notice anything and by doing so drive themselves into a corner.
Sphinx
Cryptographers looked at the whole thing. They liked the idea of using remote services and they decided to think: is it possible to do even better? Can you make a similar system, but without the drawbacks that Facebook has endowed it with?

And we decided to approach this problem in the following way: what if the password or the password hash is presented as a number? If we have the word passw0rd , it consists of 8 bytes. In almost all programming languages there are eight-byte integer types, i.e. In principle, this is the same thing. Those. 8 bytes, the word passw0rd and we can represent it as a normal decimal number. What does this give us? This gives us a completely different freedom of action. We can add passwords or hashes from them, multiply them, turn them into some other numbers. We can do real serious math operations with them.

One of the first systems that used this technology is Sphinx . She appeared a couple of years ago. This is a deterministic password manager. There are many different programs like keepass , where you have a master password and for each site it generates a random one. But there are also deterministic such things, where you enter your master password, the site you want to visit and it calculates something there and gives a unique password for each site. But of course, if this master password goes somewhere, then all passwords from your sites will be forever compromised.
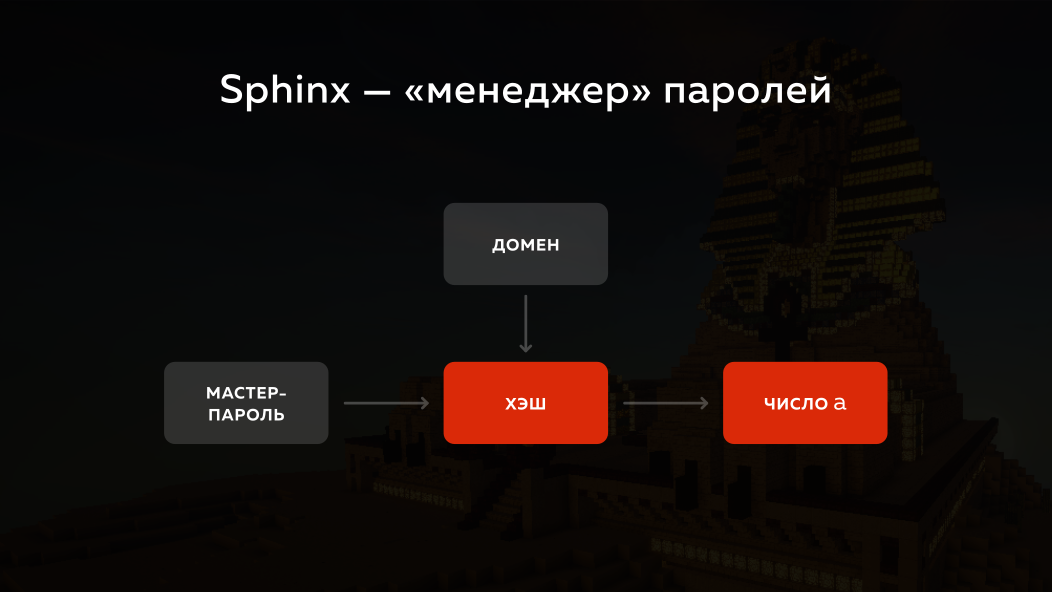
How did Sphinx approach this problem? He takes the master password, he takes the domain to which you want to go, runs the whole thing through the hash and turns it into a number. But in fact, elliptic cryptography is used there, for simplicity, I will explain all this on ordinary numbers with ordinary mathematics. He turns it into a number (let's call it a ) and what does he do next?

Absolutely wonderful thing, we can generate a large random number r each time. If we raise the number a to the power of r , and sometime later we raise this number to the power of the inverse of the number r , then we get back the same number a , right? Those. we can disguise something from the beginning, and then unmask it.
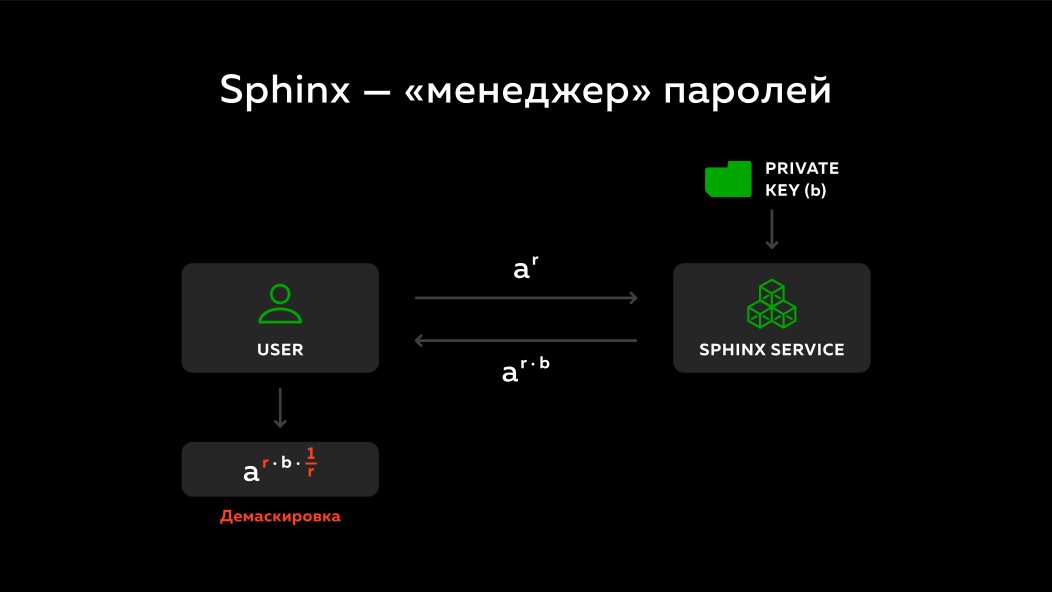
And what does the sphinx do? Again, there is a user, there is a remote service. A masked number is sent to this remote service. There is a private key on the remote service b . What is he doing? He sent the number a^r multiplies to his secret key b and sends it back. ( Note by the author of the abstract: on the slide, the number sent is not multiplied by the private key, but raised to the power of the private key, but the main point here is ). Since the number r different each time, the remote service cannot say anything about which password and domain were masked, i.e. every time he sees some different random numbers. And it multiplies simply to its private key b and sends it back.
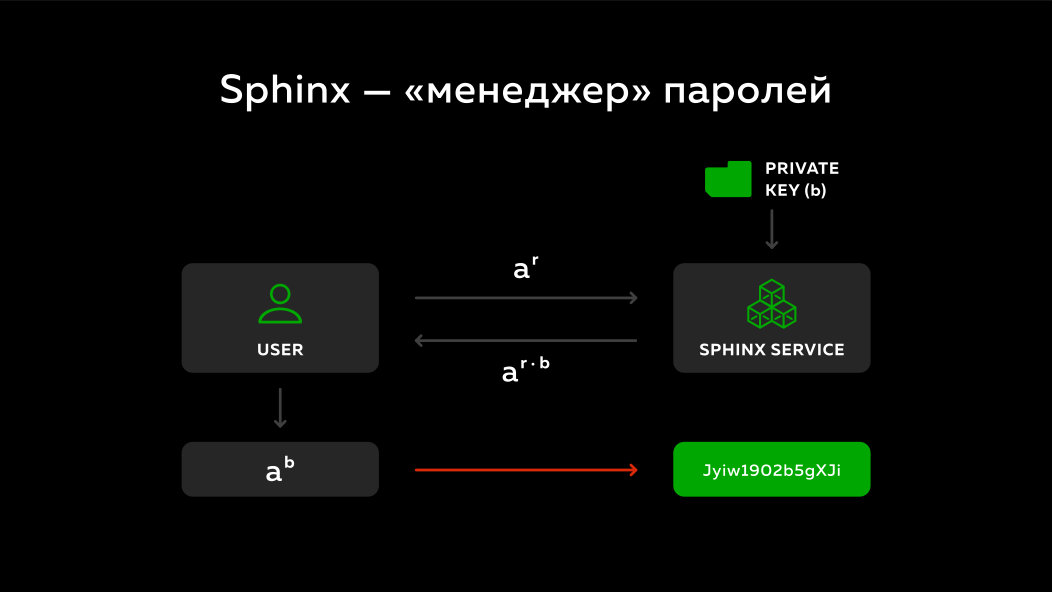
The user unmasks what the server sent him and he gets a number - his master password with the domain multiplied by the server's secret key a^b . It turns out the secret key of the server he does not know, the server does not know what the user sent him, but in the end he also gets some kind of deterministic number. Each time performing this protocol, the disguise will be different, but the result will always be the same and this result can then be turned back into some kind of password and used to log in to different sites.

Truly wonderful technology. First, you can generate large passwords, i.e. It protects against busting. Secondly, if a hacker gets access to several passwords, he will not be able to say anything about the rest, since they are generated independently of each other. Thirdly, if a user saves his master password somewhere, this will not give anything either, because hackers will not have a secret key. In the fourth, it works very quickly, because no iterative large hashes are needed here, i.e. literally 2-3 multiplications are performed and everything works instantly.
But this system has its drawbacks. The server with which the user communicates, knows nothing about him. He just gets some random numbers as input, multiplies them and sends them back. The client also does not know anything about the server, he sends something somewhere, gets the result, works well. But if something happens to the service, the user will not be able to say anything about it, he does not have information for this. The secret key also cannot be changed, nothing can be done with it.
Pythia

Can you do better?

Cryptographers looked at this system and thought, is it possible to further improve the system and supplement it with properties that would allow us to say that it corresponds to the principles of end-to-end? Those. the client can communicate with the server, but at the same time he can also authenticate him and can trust him to some extent.

And they came up with a protocol called Pythia .

He was made a wonderful man Adam Everspaugh with his colleagues. What makes it unique? First, the service knows who enters the password, i.e. The user ID is transmitted to the server by the password. It can be some random id-box that lies next to it, or just a user name. No matter. But the service knows about it. But it’s not enough that the server does not just know, it can strictly mathematically prove that it is he.

How it works? There is a backend (some kind of web service, site) and there is a Pythia service. What does the backend do and what does the service do? There is a private key k on the service, but it also transmits its public key to the backend. The backend to the service sends not only the masked number a^r , as in the Sphinx protocol, but also sends some kind of user ID ( UserID ). The service multiplies the user ID and password to its secret key and the result (UserID, a)^(r*k) sends the backend. He also sends back a certain Proof , which can be used by the backend to check the server, that it was not hacked, that it responds as it should.

Then there is a unmasking and the number y which turns out as a result is put in a DB. In the database, we have not just some kind of hash, but a number, a point of an elliptic curve.

Here are some interesting points:
- The ability for the server to combine a user ID and password into one number. This is called bilinear operation or bilinear pairing. This is a relatively new mathematics, which not so long ago began to use. She has all the properties of a new mathematician in that not even 30 years have passed in order for everyone to be convinced that everything is fine with this.
- But the
Proofthat sends the service is a rather old technology. This is called the Schnorr protocol . The generation of a public key is the multiplication of the base point by some kind of secret key. The Schnorr protocol proves that the secret key that was used to generate the public key was used to multiply the user's password by the same number too. This protocol has long been there, it is used in many places and it allows us to prove it. This is called a zero-disclosure proof - the server does not show its public key, but at the same time it says that the operation that I performed, it was performed with the private key that we initially agreed on.

What are the advantages of this system?

And she has not a lot of them.
- The system does not load the backend. Because the backend is all that does - it turns the password into a number, masks it, sends it, and then unmasks the same result.
- If a base with such numbers is stolen from you, then there is no sense in sorting passwords without a private key either.
- The Pythia service can block brute force attempts, which means the backend does not have to do this in principle. If he sees that under the same user ID they are trying to perform this transformation operation several times, he can simply cut and block everything according to the rate limit.
- Thanks to the disguise, the service knows nothing about the password. Every time a new random number is sent to him. The constant is only the user ID.
- Thanks to ZKP (Zero-knowledge proof), the backend always knows that it was the very service that he had originally addressed to him answered.
- If you have a base with hashes and salt for example, then you can migrate to this solution seamlessly for users. They may even not notice. Instead of the user's password, you take his hash, drive it into Pythia and then simply use this protocol, get the number
y, put it again in your database. The hash can then be deleted. Each time a user logs on to your system, this protocol will be executed, a number will be the result that you compare with what is in the database. The authentication system itself will remain unchanged, since users will log in as well as log in, with the same passwords, even weak ones. In this case, the system will be much more secure.

But this is not all buns.

One of the main features is that even if the Pythia service itself is hacked, you can generate a new private key. We also have a number in the database, not a hash. If we represent the old key as the number k , and the new one as the number k' , then we can calculate the number, which is called the Update token. To do this, we multiply the new number by the number opposite to the old one. And with this update token you can go through the database for each user and multiply this number y by the update token. After you have done this, your system continues to work with the new private key on the remote service. This all happens instantly. If trouble happened, your password database was stolen from you, you click on your finger to release the update token, and what hackers stole from you becomes instantly useless. You just quietly go through your background in all the records, update them and they work with the new secret key for you. Users generally do not even notice. Those. seamless update and instant password base invalidation; this is one of the key innovative features of this system.

But that's not all.

The number that lies in the database is large y , it is in principle large and looks rather pseudo-random, i.e. it's not easy to pick it up. If we transfer the functionality that we have on the backend, for example, to client devices, to phones, then we can use this one to generate keys. We called this thing BrainKey. This means that the user enters a password somewhere on the phone, also masks it, sends it to a remote service. The service returns some number y and then this y can be used to generate already some asymmetric keys. Thus, a user can get a key pair from his password. It is used in every BrainWallet . This is when you enter a password and get a bitcoin wallet generated for it. But not only cryptocurrency is limited to this application, it is a digital signature, and some backups, and account recovery, i.e. wherever asymmetric cryptography is used, where asymmetric keys are needed. All this can be used, but at the same time a key pair, and, depending on the need, you can generate as many as you like. So they will all depend on the user's password, and it is very convenient.

In a barrel of honey, as it were, not without a spoon of tar.

And the features of this technology is that it is very new. It uses an elliptic curve, which is for bilinear operations ( BLS12-381 ). Mathematics itself already exists for some time, but this particular curve, which is used in particular in our implementation, is used except for us only in
PHE

But we are thinking about whether it can be done even better? Is it possible to achieve the properties that Pythia provides, using mathematics like yesterday? Not tomorrow, not today, but even yesterday, which has been used for many years.

And literally in July of this year, scientists released a new protocol called Simple Password-Hardened Encryption Services or abbreviated PHE.

This is Russell Lai , a scientist from Europe.
What is the advantage of this service? First, it uses the standard P-256 curve, which is used everywhere, in all browsers, products, everywhere by default, which has been around for many years. Secondly, this thing works about 10 times faster than Pythia and uses standard primitives. It seems to be difficult, but it can be implemented with my own hands, without using any incomprehensible libraries. You can use OpenSSL , or Bouncy Castle , whatever.

But it works a little differently. Again, there is a backend, there is a PHE service. On the back end there is a public key, on the service there is a private key y . Unlike Pythia, the registration process and password verification process takes place a little differently. When a new user comes to the service and wants to register, what does the backend do? From the beginning, he asks the PHE service, please give me some data that I can use for registration, some Enrollment record. The service says OK and answers the backend with the following things. It generates some random 32-byte salt ( sNonce ). Based on this salt and its private key y, it generates two numbers, let's call them C0 and C1 . It also generates evidence ( Proof ) that these two numbers or there 2 points were generated using his private key y , using the Schnorr protocol (as in previous protocols). Backend Proof checks. There is no password yet. What does the backend do? He, for his part, also has his own personal client private key x and, having received the password from the user, does approximately the same thing that the service did, only adds another password there. He takes a random cNonce (random client salt) password and again generates 2 numbers HC0 and HC1 . Why 2? Because the first HC0 used for authentication, and in the second number HC1 , we also mix in some random number M multiplied by the private key x ( MC ). The M number is also 32 bytes in size and can later be used to encrypt user data (we have the same Encryption Services) ( note by the author of the abstract: the encryption key in this case will be MC ). The MC number will be available as a key only after the user has entered the correct password. It turns out at the registration stage, you can generate not only an entry for authorization, but also an encryption key, unique for each user, which can encrypt his profile, some data, something else. Then the backend simply adds what the service sent and what he did — adds these points and gets T0 and T1 . In the first case, it adds two ( C0 + HC0 ), and in the second three ( C1 + HC1 + MC ). And puts in the base 2 salts ( sNonce , cNonce ), with the help of which these numbers and 2 numbers ( T0 and T1 ) were obtained, which resulted in the sum.

Accordingly, the user authentication process occurs in reverse order. The user enters his password on the backend. The backend calculates the HC0 and from what it has in the database, subtracts the HC0 from T0 and sends the resulting C0 to the service along with the server salt. The service, knowing the server salt, calculates the same point and looks at it, it coincides with the fact that it sent a backend or not, if it matches, then the password is correct and you can answer it with the second number C1 , which it will subtract with HC1 from T1 and get the encryption key. Thus, the password for the PHE service does not even go away. He doesn't even leave the backend. It is in the form of some points multiplied by the private key of the backend. It doesn’t even exist as such, but the remote service can make a strict conclusion about whether this password is correct or not and further prove that he performed all calculations using his private key y .

What features does this system have?

Password as I said does not leave the backend. But unlike Pythia, you need a private key on the backend. Well, need and need, save somewhere. PHE has all the basic functions of Pythia:
- You can also issue update token if you have something wrong with the private key;
- You can also go through the entire database, update and everything will be as it was;
- brute force protection;
- the service knows nothing about the password;
- (Pythia , , , , PHE );
- .

...
… . . passw0rd.io . password , 18- , , zero trust, .. . , , .. Let's encrypt . , . CLI , . 2 SDK , GO .Net, .

:
- .
- .
- .

, .
?
37. ?

.
Q: , ! . , Pythia update token, ? private key . update token? Or not?
A: , update token- .
Q: . - update token-, Private key ?
A: , update token-, , - , , , update token. , .. .
Q: , , , .
A: .. .
Q: , , , - Pythia - , , , ?
A: .
Q: ?
A: , Pythia . Those. , .
Q: ( ) bcrypt ?
A: , , , .
Q: , . ? , …
A: password
Q: password ? The fire! At all.
A: 123456 , 12345, 123456.
Q: . Pythia , PHE .
A: , .
Q: . . ? production ?
A: . BUT! Pythia.
Q: Pythia, , ?
A: .
Q: , ?
A: .
Q: , , !
A: SDK, .
Q: , , , , .. - , ? ? ?
A: , , , .. PHE, , 5 2 , 2 5 . , . PHE ( , ), , 10 , .
Q: .. - , - ? ?
A: . rate limiting, , .
Q: .. , ?
A: .
Q: . , .. Pythia (), , ? ?
A: , , .
Q: , update ?
A: , Pythia , , - - , , , )
A: ? Thank you all so much! . , , PHE, , .
findings
PHE ( ) + — ( , , ) ( ). PHE , .
:
- ( ) ;
- ( ).
, .
Scratch Virgil Security , , !
( )?
UPD : Scratch . . , . .
')
Source: https://habr.com/ru/post/434708/
All Articles
