Two-phase commit and the future of distributed systems
In this article, we will model and investigate a two-phase commit protocol using TLA +.
The two-phase commit protocol is practical and is used today in many distributed systems. However, it is rather short. Therefore, we can quickly simulate it and learn a lot. In fact, with this example we will illustrate what result is fundamentally impossible in distributed systems.
The transaction goes through resource managers (RM) . All RMs must agree on whether the transaction will be completed or aborted .
')
The transaction manager (TM) makes the final decision: commit or cancel . The prerequisite for a commit is a commitment to committing all RMs. Otherwise, the transaction should be canceled.
For simplicity, we perform simulations in a shared memory model, not in a messaging system. It also provides quick model validation. But we will add non-atomicity to the “read from neighboring node and state update” actions to capture interesting behavior in message passing.
RM can only read the TM state and read / update its own state. He cannot read the status of another resource manager. TM can read the status of all RM nodes and read / update its own state.

Lines 9-10 set the initial
The predicate

TM modeling is simple. The transaction manager checks for commit or cancellation — and updates
There is a possibility that TM will not be able to make

The RM model is also simple. Since the “working” and “prepared” states are non-finite, RM selects non-deterministic among the actions until it reaches the final state. The “working” RM can go to the “interrupted” or “prepared” state. A “prepared” RM expects a commit / cancel from TM, and acts accordingly. The figure below shows the possible state transitions for one RM. But note that we have several RMs, each of which passes through its own states at its own pace without knowing the status of other RMs.
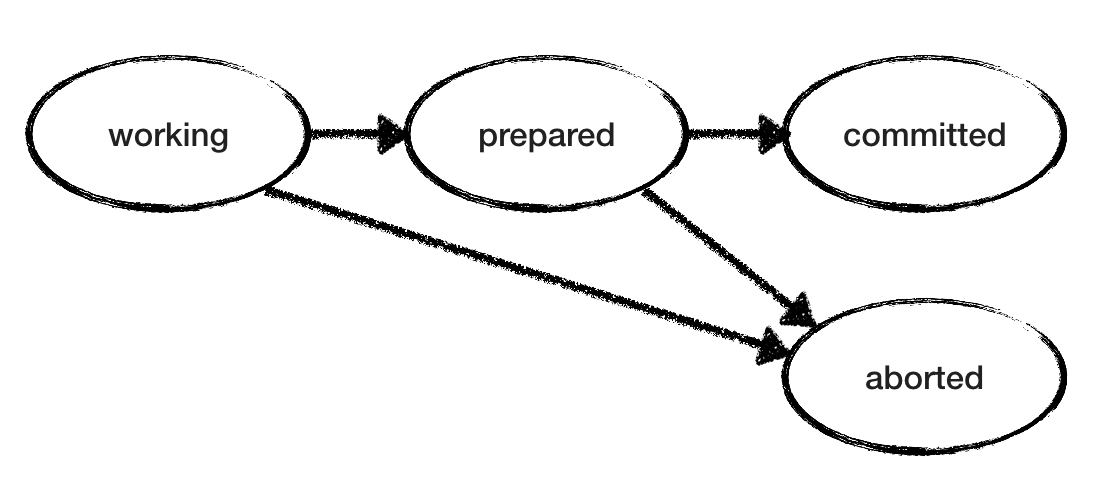

We need to check the consistency of our two-phase commit: so that there are no different RMs, one of which says “commit” and the other “abortion”.
Now we are ready to check the protocol model. Initially, we set

Now set

We see that at the
To avoid transaction freezes, we add a backup TM (BTM), which quickly takes control if the main TM is unavailable. For decision making, BTM uses the same logic as TM. And for simplicity, we assume that BTM never falls.

When we check the model with the added BTM process, we get a new error message.

BTM cannot accept a commit, because our original condition

Success! When we check the model, we achieve both consistency and completeness, since the BTM takes control and completes the transaction if TM drops. Here is the 2PCwithBTM model in TLA + (BTM and the second line canCommit were originally unpacked) and the corresponding pdf .
We assumed that RM is reliable. Now cancel this condition and see how the protocol behaves when RM fails. Add the "unavailable" state to the failure model. To investigate the behavior and model intermittent loss of accessibility, let the emergency RM recover and continue working by reading its status from the log. Here is another RM state transition diagram with the “unavailable” state added and red transitions. Below is the revised model for RM.
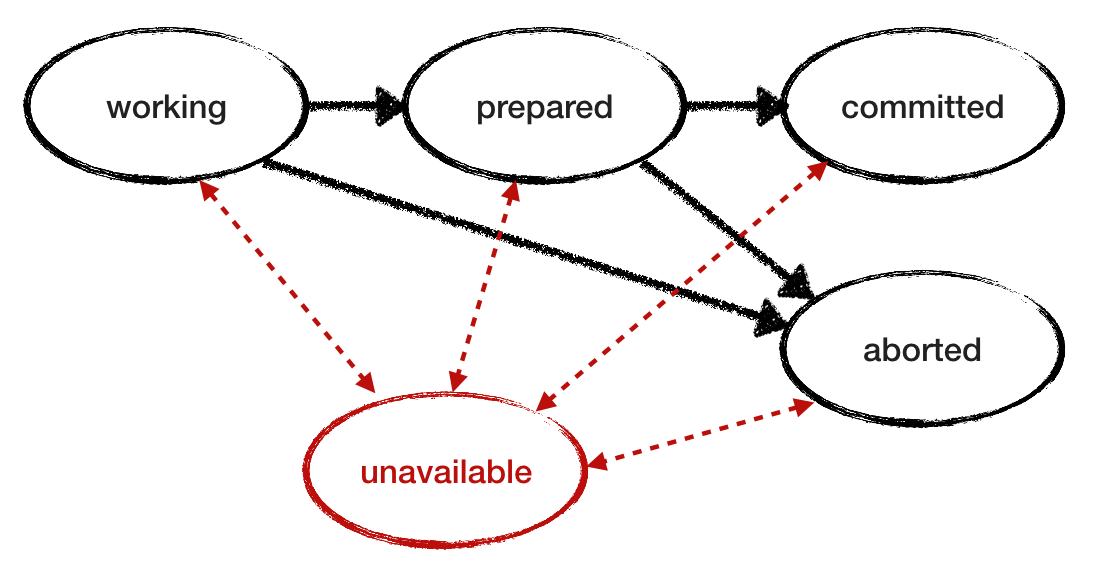

It is also necessary to modify
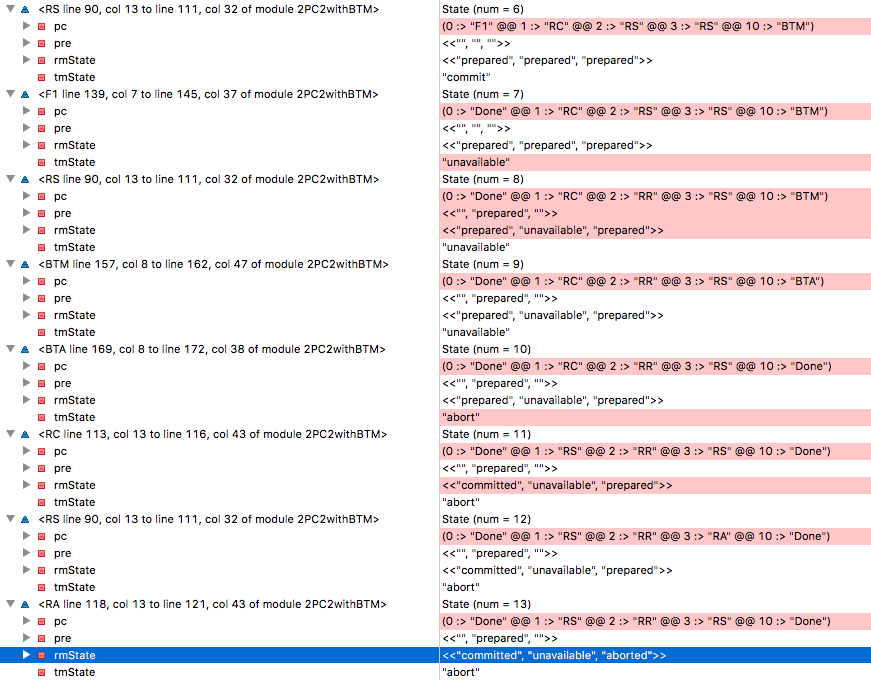
When we check the model, the inconsistency problem arises! How could this happen? We trace the trace.
With
In this case, the BTM made a decision that broke the consistency . On the other hand, if you force the BTM to wait for the RM to exit from the inaccessible state, it may hang forever in the event of a crash on the node, and this will violate the condition for fulfillment (progress).
An updated TLA + model file is available here , as well as the corresponding pdf .
So what happened? We have stumbled into the theorem of Fisher, Lynch, Paterson (FLP) about the impossibility of consensus in an asynchronous system with failures.
In our example, the BTM cannot correctly decide whether RM2 is in a state of failure or not — and it is incorrect to decide to abort the transaction. If only the original TM made the decision, such an inaccuracy in recognizing the failure would not have become a problem. RM will comply with any TM decision, so both consistency and implementation progress will be maintained.
The problem is that we have two objects make decisions: TM and BTM, they look at the state of RM at different times and make different decisions. Such asymmetric information is the root of all evil in distributed systems.
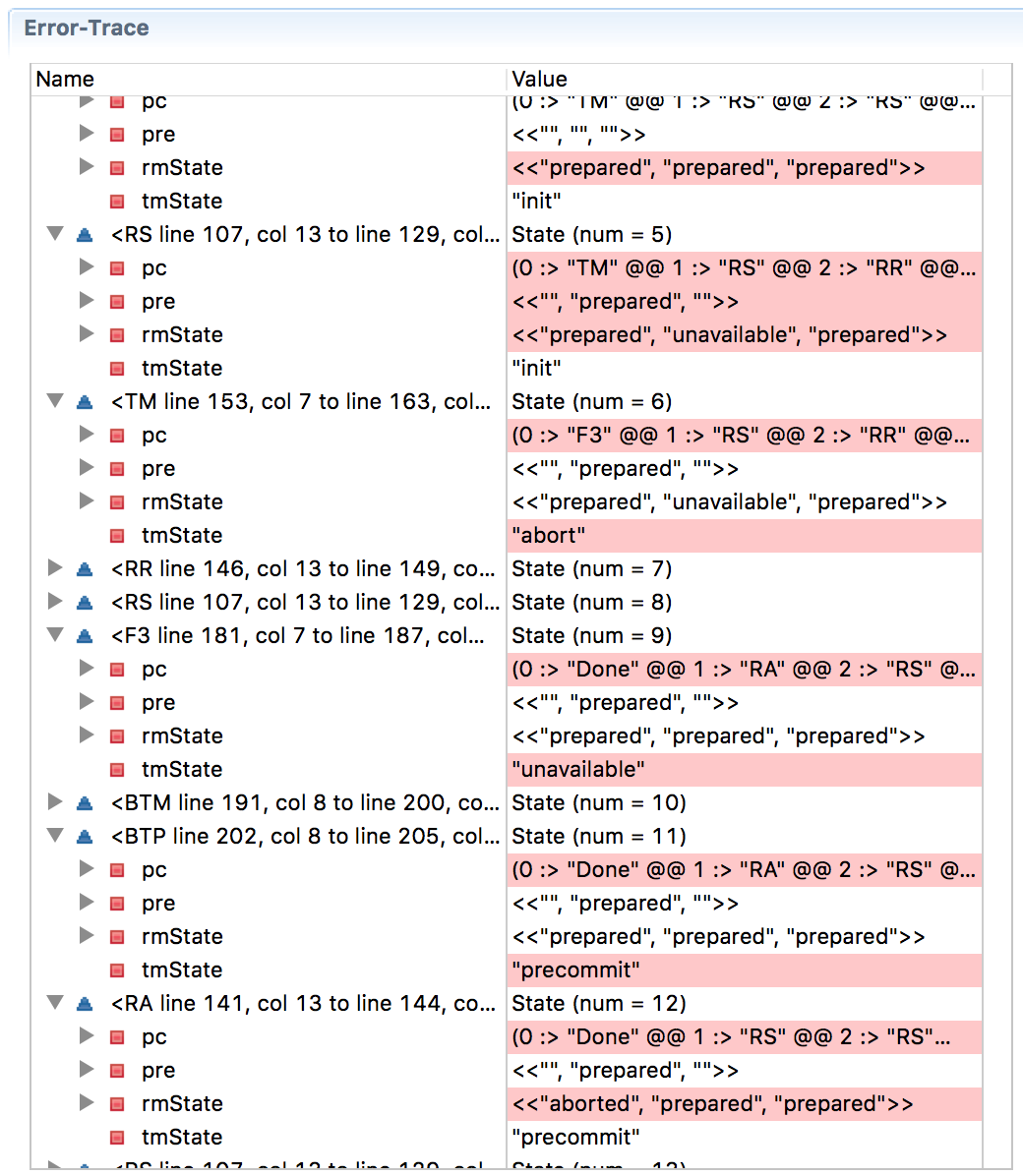
The problem does not disappear even with the extension to a three-phase commit. Here is a three-phase commit modeled in TLA + ( pdf version ), and the error tracing below shows that progress has been broken this time (on the Wikipedia page on the three-phase commit, the situation is described when RM1 hangs after receiving the solution before the commit and RM2 and RM3 commit commit, which violates consistency).

But all is not lost, hope is not dead. We have Paxos . It acts neatly within the FLP theorem. The innovation of Paxos is that it is always safe (even in the presence of inaccurate detectors, asynchronous execution and failures), and ultimately ends the transaction when consensus becomes possible.
You can emulate TM on a cluster with three Paxos nodes, and this solves the inconsistency problem of TM / BTM. Or, as Gray and Lamport showed in a scientific article on consensus in a commit transaction , if RM uses the Paxos container to store its decisions at the same time as the TM response, this eliminates one extra step in the standard protocol algorithm.
The two-phase commit protocol is practical and is used today in many distributed systems. However, it is rather short. Therefore, we can quickly simulate it and learn a lot. In fact, with this example we will illustrate what result is fundamentally impossible in distributed systems.
The problem of two-phase commit
The transaction goes through resource managers (RM) . All RMs must agree on whether the transaction will be completed or aborted .
')
The transaction manager (TM) makes the final decision: commit or cancel . The prerequisite for a commit is a commitment to committing all RMs. Otherwise, the transaction should be canceled.
Some notes on modeling
For simplicity, we perform simulations in a shared memory model, not in a messaging system. It also provides quick model validation. But we will add non-atomicity to the “read from neighboring node and state update” actions to capture interesting behavior in message passing.
RM can only read the TM state and read / update its own state. He cannot read the status of another resource manager. TM can read the status of all RM nodes and read / update its own state.
Definitions

Lines 9-10 set the initial
rmState for each RM to working , and TM to init .The predicate
canCommit is true if all RMs are “prepared” (ready for commit). If there is a RM in the "hang up" state, then the predicate canAbort becomes canAbort .
TM modeling is simple. The transaction manager checks for commit or cancellation — and updates
tmState .There is a possibility that TM will not be able to make
tmState “inaccessible”, but only if the TMMAYFAIL constant TMMAYFAIL set to true before starting the model check. In TLA +, labels define the degree of atomicity, that is, its granularity. By the labels F1 and F2 we denote that the corresponding operators are executed nonatomic (after some indefinite time) with respect to the previous operators.RM Model

The RM model is also simple. Since the “working” and “prepared” states are non-finite, RM selects non-deterministic among the actions until it reaches the final state. The “working” RM can go to the “interrupted” or “prepared” state. A “prepared” RM expects a commit / cancel from TM, and acts accordingly. The figure below shows the possible state transitions for one RM. But note that we have several RMs, each of which passes through its own states at its own pace without knowing the status of other RMs.

Two Phase Commit Model

We need to check the consistency of our two-phase commit: so that there are no different RMs, one of which says “commit” and the other “abortion”.
Completed predicate verifies that the protocol does not hang forever: in the end, each RM reaches the committed or aborted final state.Now we are ready to check the protocol model. Initially, we set
TMMAYFAIL=FALSE, RM=1..3 to run the protocol with three RMs and one TM, that is, in a reliable configuration. Verifying the model takes 15 seconds and says that there are no errors. Both Consistency and Completed satisfied with any possible protocol execution with any alternation of RM actions and TM actions.
Now set
TMMAYFAIL=TRUE and restart the check. The program quickly produces the opposite result, where RM is stuck waiting for a response from an inaccessible TM.
We see that at the
State=4 stage, the RM2 transitions are interrupted, the RM3 transitions are interrupted at State=7 , the State=8 TM goes into the “hang up” state and falls to the State=9 . At State=10 system freezes because RM1 remains in a prepared state forever, awaiting a decision from a fallen TM.BTM simulation
To avoid transaction freezes, we add a backup TM (BTM), which quickly takes control if the main TM is unavailable. For decision making, BTM uses the same logic as TM. And for simplicity, we assume that BTM never falls.

When we check the model with the added BTM process, we get a new error message.

BTM cannot accept a commit, because our original condition
canCommit states that all RMstates must be “prepared” and do not take into account the condition that some RMs have already received a decision on a commit from the original TM before BTM took control. It is necessary to rewrite canCommit conditions taking into account this situation.
Success! When we check the model, we achieve both consistency and completeness, since the BTM takes control and completes the transaction if TM drops. Here is the 2PCwithBTM model in TLA + (BTM and the second line canCommit were originally unpacked) and the corresponding pdf .
What if RM fails too?
We assumed that RM is reliable. Now cancel this condition and see how the protocol behaves when RM fails. Add the "unavailable" state to the failure model. To investigate the behavior and model intermittent loss of accessibility, let the emergency RM recover and continue working by reading its status from the log. Here is another RM state transition diagram with the “unavailable” state added and red transitions. Below is the revised model for RM.


It is also necessary to modify
canAbort , taking into account the state of inaccessibility. TM may decide to “hang up” if any of the services is in an interrupted or inaccessible state. If you omit this condition, then the fallen and not restored RM will interrupt the progress of the transaction. Of course, again, it is necessary to take into account the RMs, who have learned the transaction completion decision from the source TM.Model checking

When we check the model, the inconsistency problem arises! How could this happen? We trace the trace.
With
State=6 all RMs are in a prepared state, TM decided to complete the transaction, RM1 saw this decision and switched to RC tag, which means it is ready to change its state to “completed”. (Memorize RM1, this gun will fire in the last act). Unfortunately, TM collapses at State=7 , and RM2 becomes unavailable at State=8 . In the ninth step, the backup BTM takes control and reads the state of the three RMs as “prepared, unavailable, prepared” - and decides to cancel the transaction in the tenth step. Remember RM1? He decides to complete the transaction, because he received such a decision from the original TM, and goes into the committed state at the 11th step. In State=13 RM3 executes the decision to abort the transaction from the BTM and goes into the aborted state - and now we have broken consistency with RM1.In this case, the BTM made a decision that broke the consistency . On the other hand, if you force the BTM to wait for the RM to exit from the inaccessible state, it may hang forever in the event of a crash on the node, and this will violate the condition for fulfillment (progress).
An updated TLA + model file is available here , as well as the corresponding pdf .
Impossibility of FLP
So what happened? We have stumbled into the theorem of Fisher, Lynch, Paterson (FLP) about the impossibility of consensus in an asynchronous system with failures.
In our example, the BTM cannot correctly decide whether RM2 is in a state of failure or not — and it is incorrect to decide to abort the transaction. If only the original TM made the decision, such an inaccuracy in recognizing the failure would not have become a problem. RM will comply with any TM decision, so both consistency and implementation progress will be maintained.
The problem is that we have two objects make decisions: TM and BTM, they look at the state of RM at different times and make different decisions. Such asymmetric information is the root of all evil in distributed systems.
The problem does not disappear even with the extension to a three-phase commit. Here is a three-phase commit modeled in TLA + ( pdf version ), and the error tracing below shows that progress has been broken this time (on the Wikipedia page on the three-phase commit, the situation is described when RM1 hangs after receiving the solution before the commit and RM2 and RM3 commit commit, which violates consistency).

Paxos is trying to make the world better

But all is not lost, hope is not dead. We have Paxos . It acts neatly within the FLP theorem. The innovation of Paxos is that it is always safe (even in the presence of inaccurate detectors, asynchronous execution and failures), and ultimately ends the transaction when consensus becomes possible.
You can emulate TM on a cluster with three Paxos nodes, and this solves the inconsistency problem of TM / BTM. Or, as Gray and Lamport showed in a scientific article on consensus in a commit transaction , if RM uses the Paxos container to store its decisions at the same time as the TM response, this eliminates one extra step in the standard protocol algorithm.
Source: https://habr.com/ru/post/434496/
All Articles