Depth accuracy clearly
Depth accuracy is a pain in the ass, which sooner or later any graphics programmer faces. Many articles and papers have been written on this topic. And in different games and engines, and on different platforms, you can see a lot of different formats and settings for the depth buffer .
The transformation of depth on the GPU does not seem obvious because of how it interacts with the perspective projection, and the study of equations does not clarify the situation. To understand how this works, it is useful to draw some pictures.

')
This article is divided into 3 parts:
Hardware GPU depth buffer usually does not store a linear representation of the distance between the object and the camera, contrary to what is naively expected from it at the first meeting. Instead, depth buffer stores values inversely proportional to the depth of the view-space. I want to briefly describe the motivation for such a decision.
In this article I will use d to represent the values stored in the depth buffer (in the range [0, 1] for DirectX), and z to represent the depth view-space, i.e. real distance from the camera, in world units, for example, meters. In general, the relationship between them is as follows:
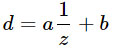
where a, b are constants associated with the near and far settings of the planes. In other words, d is always some linear transformation from 1 / z .
At first glance it may seem that as d you can take any function of z . So why does she look that way? There are two main reasons for this.
First, 1 / z naturally fits into the perspective projection framework. And this is the most basic class of transformations, which is guaranteed to keep straight. Therefore, the perspective projection is suitable for hardware rasterization, since the straight edges of the triangles remain straight on the screen. We can obtain a linear transformation from 1 / z , taking advantage of the promising division, which the GPU already performs:
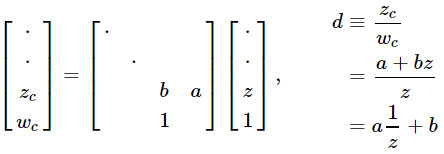
Of course, the real strength of this approach is that the projection matrix can be multiplied with other matrices, allowing you to combine many transformations into one.
The second reason is that 1 / z is linear in the screen space (screen space), as noted by Emil Persson . This makes it easy to interpolate d in a triangle during rasterization, and things like hierarchical Z-buffers , early Z-culling and compression depth buffer .
Equations are hard, let's look at a couple of pictures!
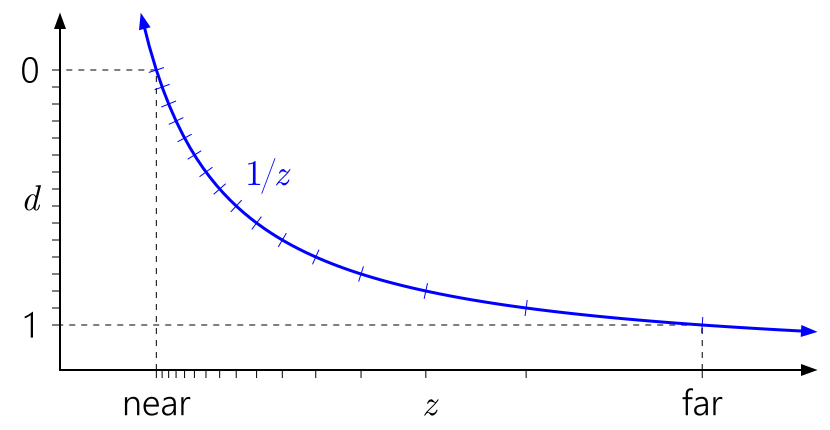
The way to read these graphs: from left to right, then down. Start with d on the left axis. Since d can be an arbitrary linear transformation from 1 / z , we can arrange 0 and 1 to any convenient place on the axis. The marks indicate different depth buffer . For the sake of clarity, I am modeling a 4-bit integer normalized depth buffer , so there are 16 evenly spaced marks.
The graph above shows the “standard” vanilla depth conversion in D3D and similar APIs. You can immediately see how, due to the 1 / z curve, the values close to the near plane are grouped, and the values close to the far plane are scattered.
It is also easy to see why the near plane influences depth accuracy so much. Distance to the near plane will lead to a rapid increase in d values relative to z values, which will lead to an even more uneven distribution of values:
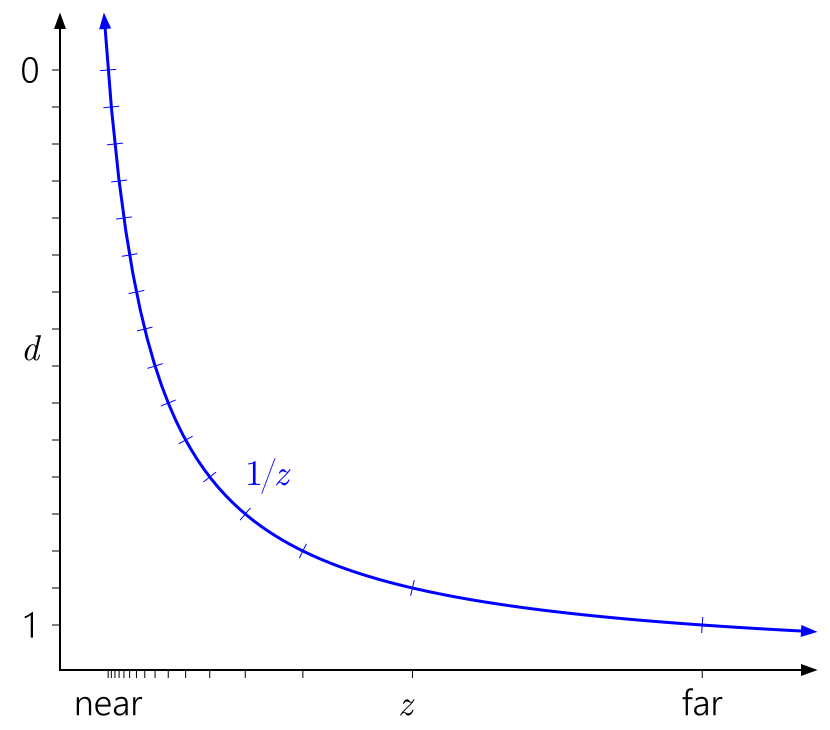
Similarly, in this context, it is easy to see why moving a far plane to infinity does not have such a large effect. It simply means extending the range d to 1 / z = 0 :
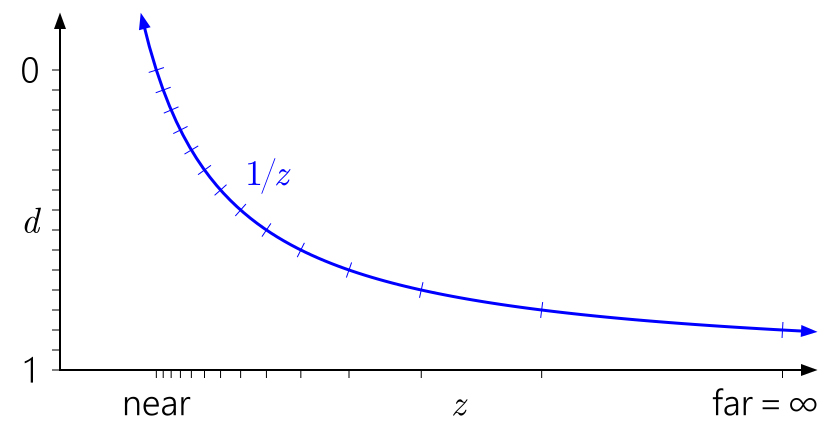
But what about floating-point depth? The following graph adds marks corresponding to a float format with 3 bits of exponent and 3 bits of mantissa:
Now in the range [0,1] there are 40 different values - a little more than 16 values earlier, but most of them are uselessly grouped close to the near plane (closer to 0, float has higher accuracy), where we really don’t need greater accuracy.
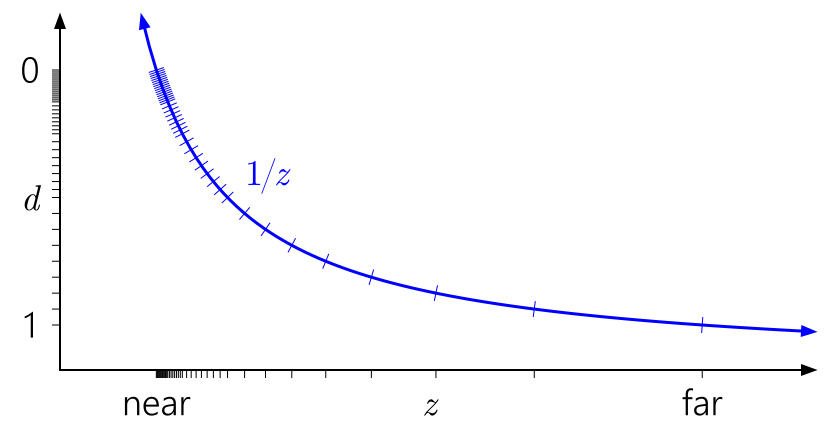
Now a well-known trick is to invert the depth, displaying the near plane on d = 1 and the far plane on d = 0 :
Much better! Now the quasi-logarithmic distribution of float somehow compensates for the nonlinearity of 1 / z , while closer to the near plane gives an accuracy similar to the integer depth buffer, and gives a much greater accuracy elsewhere. The accuracy of the depth deteriorates very slowly if you move further away from the camera.
The reversed-Z trick may have been reinvented independently several times, but at least the first mention was in SIGGRAPH '99 paper [Eugene Lapidous and Guofang Jiao (unfortunately not publicly available)]. And recently he was re-mentioned on the blog by Matt Petineo and Brano Kemen , and in the speech of Emil Persson, Creating Vast Game Worlds SIGGRAPH 2012.
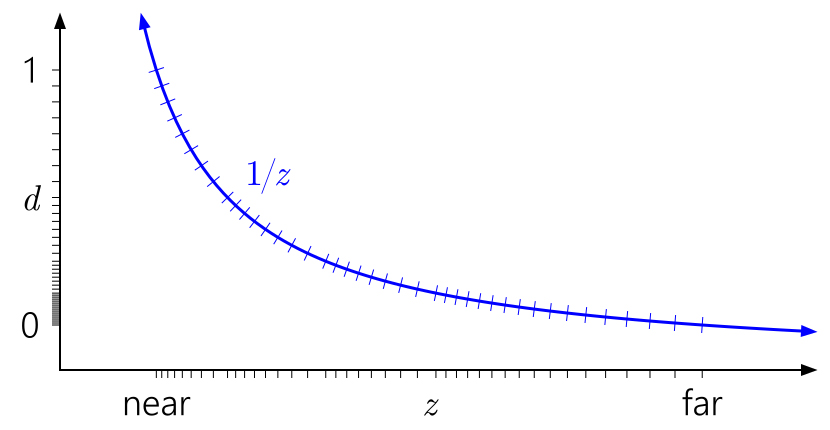
All previous graphics assumed the depth [0,1] range after projection, which is an agreement in D3D. What about OpenGL ?
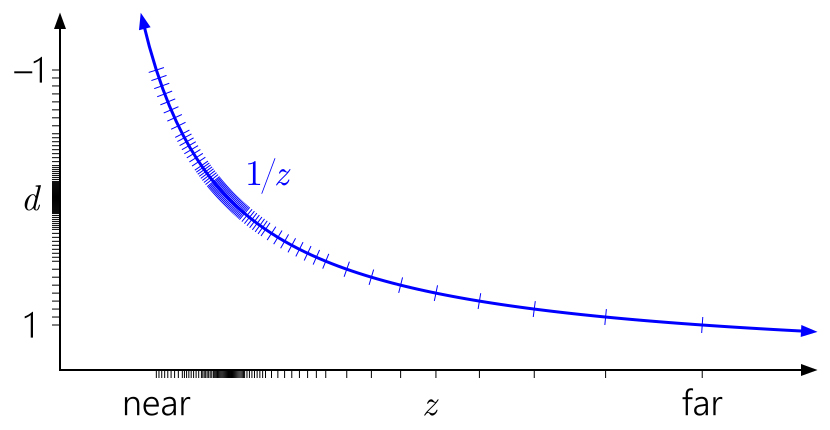
OpenGL defaults to the depth [-1, 1] range after projection. For integer formats, nothing changes, but for a floating point all accuracy is concentrated in the middle uselessly. (The depth value is mapped to the [0,1] range for subsequent storage in the depth buffer, but this does not help, since the initial mapping to [-1,1] has already destroyed all accuracy in the far half of the range.) And because of the symmetry, the trick reversed-Z won't work here.
Fortunately, this can be fixed in the desktop OpenGL using the widely supported ARB_clip_control extension (also starting with OpenGL 4.5, glClipControl is included in the standard). Unfortunately, the GL ES in the span.
The 1 / z conversion and the choice of float vs int depth buffer is a big part of the accuracy story, but not all. Even if you have enough depth depth to represent the scene you are trying to render, it is easy to degrade the accuracy with arithmetic errors during the vertex conversion process.
At the beginning of the article it was mentioned that Upchurch and Desbrun studied this problem. They offered two basic recommendations for minimizing rounding errors:
Upchurch and Desbrun compiled these recommendations using an analytical method based on processing round-off errors as small random errors presented in each arithmetic operation, and tracking them until the first order in the conversion process. I decided to test the results in practice.
The sources here are Python 3.4 and numpy. The program works as follows: a sequence of random points is generated, ordered by depth, located linearly or logarithmically between the near and far planes. Then the points are multiplied by the view and projection of the matrix and the perspective division is performed, 32-bit floats are used, and optionally the final result is converted into a 24-bit int. At the end, the sequence is followed by counting how many times 2 neighboring points (which initially had different depths) either became identical, as their total depth coincided, or the order changed in general. In other words, the program measures the frequency with which depth comparison errors occur - which corresponds to issues such as Z-fighting - under various scenarios.
Here are the results for near = 0.1, far = 10K, with a linear depth of 10K. (I tried the logarithmic depth interval and other near / far relationships, and although specific numbers varied, the overall trends in the results were the same.)
In the table, “eq” - two points with the nearest depth get the same value in the depth buffer, and “swap” - two points with the nearest depth are swapped.
I apologize for the fact that without graphics, the dimension is too large and just can not build it! In any case, looking at the numbers, the following conclusions are obvious:
However, the above conclusions do not have a real value compared to the magic reversed-Z . Check:
I think the conclusion here is clear. In any situation, when dealing with perspective projection, simply use the float depth buffer and reversed-Z ! And if you can't use the float depth buffer, you should still use reversed-Z. This is not a panacea for all ills, especially if you create an open-world environment with extreme depth ranges. But this is a great start.
The transformation of depth on the GPU does not seem obvious because of how it interacts with the perspective projection, and the study of equations does not clarify the situation. To understand how this works, it is useful to draw some pictures.

')
This article is divided into 3 parts:
- I will try to explain the motivation of the nonlinear depth conversion.
- I will present several graphs that will help you understand how nonlinear depth conversion works in different situations, intuitively and visually.
- Discussion of the main findings of Tightening the Precision of Perspective Rendering [Paul Upchurch, Mathieu Desbrun (2012)] concerning the effect of round-off floating-point error on depth accuracy.
Why 1 / z?
Hardware GPU depth buffer usually does not store a linear representation of the distance between the object and the camera, contrary to what is naively expected from it at the first meeting. Instead, depth buffer stores values inversely proportional to the depth of the view-space. I want to briefly describe the motivation for such a decision.
In this article I will use d to represent the values stored in the depth buffer (in the range [0, 1] for DirectX), and z to represent the depth view-space, i.e. real distance from the camera, in world units, for example, meters. In general, the relationship between them is as follows:
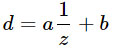
where a, b are constants associated with the near and far settings of the planes. In other words, d is always some linear transformation from 1 / z .
At first glance it may seem that as d you can take any function of z . So why does she look that way? There are two main reasons for this.
First, 1 / z naturally fits into the perspective projection framework. And this is the most basic class of transformations, which is guaranteed to keep straight. Therefore, the perspective projection is suitable for hardware rasterization, since the straight edges of the triangles remain straight on the screen. We can obtain a linear transformation from 1 / z , taking advantage of the promising division, which the GPU already performs:
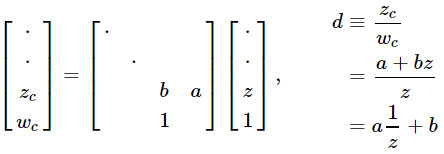
Of course, the real strength of this approach is that the projection matrix can be multiplied with other matrices, allowing you to combine many transformations into one.
The second reason is that 1 / z is linear in the screen space (screen space), as noted by Emil Persson . This makes it easy to interpolate d in a triangle during rasterization, and things like hierarchical Z-buffers , early Z-culling and compression depth buffer .
Short from article
While the value of w (view-space depth) is linear in the view space, it is non-linear in the screen space. z (depth) , non-linear in the view space, on the other hand, is linear in the screen space. This can be easily verified with a simple DX10 shader:
Here In.position is SV_Position. The result looks something like this:

Notice that all surfaces look monochrome. The difference in z from pixel to pixel is the same for any primitive. This is very important for the GPU. One of the reasons is that z interpolation is cheaper than w interpolation. For z, it is not necessary to perform a perspective correction. With cheaper hardware units, you can handle more pixels per cycle with the same transistor budget. Naturally, this is very important for the pre-z pass and shadow map . With modern hardware, linearity in the screen space is also a very useful feature for z-optimizations. Given that the gradient is linear for the entire primitive, it is also relatively easy to calculate the exact depth range within the tile for Hi-z culling . This also means that z-compression is possible. With the constant Δz in x and y, you do not need to store a lot of information to be able to fully restore all z values in the tile, provided that the primitive covered the entire tile.
float dx = ddx(In.position.z); float dy = ddy(In.position.z); return 1000.0 * float4(abs(dx), abs(dy), 0, 0); Here In.position is SV_Position. The result looks something like this:

Notice that all surfaces look monochrome. The difference in z from pixel to pixel is the same for any primitive. This is very important for the GPU. One of the reasons is that z interpolation is cheaper than w interpolation. For z, it is not necessary to perform a perspective correction. With cheaper hardware units, you can handle more pixels per cycle with the same transistor budget. Naturally, this is very important for the pre-z pass and shadow map . With modern hardware, linearity in the screen space is also a very useful feature for z-optimizations. Given that the gradient is linear for the entire primitive, it is also relatively easy to calculate the exact depth range within the tile for Hi-z culling . This also means that z-compression is possible. With the constant Δz in x and y, you do not need to store a lot of information to be able to fully restore all z values in the tile, provided that the primitive covered the entire tile.
Depth chart graphics
Equations are hard, let's look at a couple of pictures!

The way to read these graphs: from left to right, then down. Start with d on the left axis. Since d can be an arbitrary linear transformation from 1 / z , we can arrange 0 and 1 to any convenient place on the axis. The marks indicate different depth buffer . For the sake of clarity, I am modeling a 4-bit integer normalized depth buffer , so there are 16 evenly spaced marks.
The graph above shows the “standard” vanilla depth conversion in D3D and similar APIs. You can immediately see how, due to the 1 / z curve, the values close to the near plane are grouped, and the values close to the far plane are scattered.
It is also easy to see why the near plane influences depth accuracy so much. Distance to the near plane will lead to a rapid increase in d values relative to z values, which will lead to an even more uneven distribution of values:

Similarly, in this context, it is easy to see why moving a far plane to infinity does not have such a large effect. It simply means extending the range d to 1 / z = 0 :

But what about floating-point depth? The following graph adds marks corresponding to a float format with 3 bits of exponent and 3 bits of mantissa:

Now in the range [0,1] there are 40 different values - a little more than 16 values earlier, but most of them are uselessly grouped close to the near plane (closer to 0, float has higher accuracy), where we really don’t need greater accuracy.
Now a well-known trick is to invert the depth, displaying the near plane on d = 1 and the far plane on d = 0 :

Much better! Now the quasi-logarithmic distribution of float somehow compensates for the nonlinearity of 1 / z , while closer to the near plane gives an accuracy similar to the integer depth buffer, and gives a much greater accuracy elsewhere. The accuracy of the depth deteriorates very slowly if you move further away from the camera.
The reversed-Z trick may have been reinvented independently several times, but at least the first mention was in SIGGRAPH '99 paper [Eugene Lapidous and Guofang Jiao (unfortunately not publicly available)]. And recently he was re-mentioned on the blog by Matt Petineo and Brano Kemen , and in the speech of Emil Persson, Creating Vast Game Worlds SIGGRAPH 2012.
All previous graphics assumed the depth [0,1] range after projection, which is an agreement in D3D. What about OpenGL ?

OpenGL defaults to the depth [-1, 1] range after projection. For integer formats, nothing changes, but for a floating point all accuracy is concentrated in the middle uselessly. (The depth value is mapped to the [0,1] range for subsequent storage in the depth buffer, but this does not help, since the initial mapping to [-1,1] has already destroyed all accuracy in the far half of the range.) And because of the symmetry, the trick reversed-Z won't work here.
Fortunately, this can be fixed in the desktop OpenGL using the widely supported ARB_clip_control extension (also starting with OpenGL 4.5, glClipControl is included in the standard). Unfortunately, the GL ES in the span.
The effect of rounding error
The 1 / z conversion and the choice of float vs int depth buffer is a big part of the accuracy story, but not all. Even if you have enough depth depth to represent the scene you are trying to render, it is easy to degrade the accuracy with arithmetic errors during the vertex conversion process.
At the beginning of the article it was mentioned that Upchurch and Desbrun studied this problem. They offered two basic recommendations for minimizing rounding errors:
- Use infinite far plane.
- Keep the projection matrix separate from other matrices, and apply it as a separate operation in the vertex shader, and not combine it with the view matrix.
Upchurch and Desbrun compiled these recommendations using an analytical method based on processing round-off errors as small random errors presented in each arithmetic operation, and tracking them until the first order in the conversion process. I decided to test the results in practice.
The sources here are Python 3.4 and numpy. The program works as follows: a sequence of random points is generated, ordered by depth, located linearly or logarithmically between the near and far planes. Then the points are multiplied by the view and projection of the matrix and the perspective division is performed, 32-bit floats are used, and optionally the final result is converted into a 24-bit int. At the end, the sequence is followed by counting how many times 2 neighboring points (which initially had different depths) either became identical, as their total depth coincided, or the order changed in general. In other words, the program measures the frequency with which depth comparison errors occur - which corresponds to issues such as Z-fighting - under various scenarios.
Here are the results for near = 0.1, far = 10K, with a linear depth of 10K. (I tried the logarithmic depth interval and other near / far relationships, and although specific numbers varied, the overall trends in the results were the same.)
In the table, “eq” - two points with the nearest depth get the same value in the depth buffer, and “swap” - two points with the nearest depth are swapped.
| Composite view-projection matrix | Separate view and projection matrix | |||
| float32 | int24 | float32 | int24 | |
| Unchanged Z values (control test) | 0% eq 0% swap | 0% eq 0% swap | 0% eq 0% swap | 0% eq 0% swap |
| Standard projection | 45% eq 18% swap | 45% eq 18% swap | 77% eq 0% swap | 77% eq 0% swap |
| Infinite far | 45% eq 18% swap | 45% eq 18% swap | 76% eq 0% swap | 76% eq 0% swap |
| Reversed z | 0% eq 0% swap | 76% eq 0% swap | 0% eq 0% swap | 76% eq 0% swap |
| Infinite + reversed-Z | 0% eq 0% swap | 76% eq 0% swap | 0% eq 0% swap | 76% eq 0% swap |
| Standard + GL-style | 56% eq 12% swap | 56% eq 12% swap | 77% eq 0% swap | 77% eq 0% swap |
| Infinite + GL-style | 59% eq 10% swap | 59% eq 10% swap | 77% eq 0% swap | 77% eq 0% swap |
I apologize for the fact that without graphics, the dimension is too large and just can not build it! In any case, looking at the numbers, the following conclusions are obvious:
- In most cases, there is no difference between int and float depth buffer . Arithmetic errors of depth calculation overlap conversion errors to int. Partially because float32 and int24 are almost equal to the ULP (the unit of least precision is the distance to the nearest adjacent number) by [0.5.1] (since float32 has a 23-bit mantissa), so almost the entire depth range does not add a conversion error in int.
- In most cases, the separation of view and projection matrices (following the recommendations of Upchurch and Desbrun) improves the result. Despite the fact that the overall error rate does not decrease, “swaps” become equal values, and this is a step in the right direction.
- The infinite far plane slightly changes the error rate. Upchurch and Desbrun predicted a 25% reduction in the frequency of numerical errors (accuracy errors), but this does not seem to lead to a decrease in the frequency of comparison errors.
However, the above conclusions do not have a real value compared to the magic reversed-Z . Check:
- Reversed-Z with float depth buffer gives zero error rate in the test. Now, of course, you may get some errors if you continue to increase the interval of input depth values. However, reversed-Z with float is ridiculously more accurate than any other option.
- Reversed-Z with integer depth buffer is as good as other integer options.
- Reversed-Z erases the differences between the composite and separate view / projection matrices, and the finite and infinite far planes. In other words, with reversed-Z, you can multiply the projection with other matrices, and use any far plane you want without compromising accuracy.
Conclusion
I think the conclusion here is clear. In any situation, when dealing with perspective projection, simply use the float depth buffer and reversed-Z ! And if you can't use the float depth buffer, you should still use reversed-Z. This is not a panacea for all ills, especially if you create an open-world environment with extreme depth ranges. But this is a great start.
Source: https://habr.com/ru/post/434322/
All Articles