Amateur mathematician found the smallest universal coverage

Through difficult geometric calculations, Philip Gibbs discovered the smallest known coating for any possible shape.

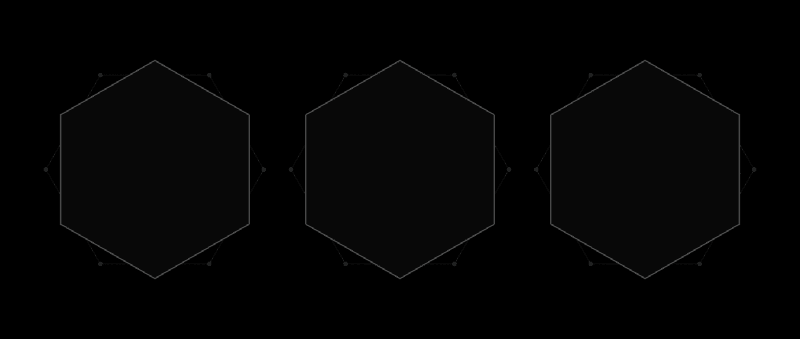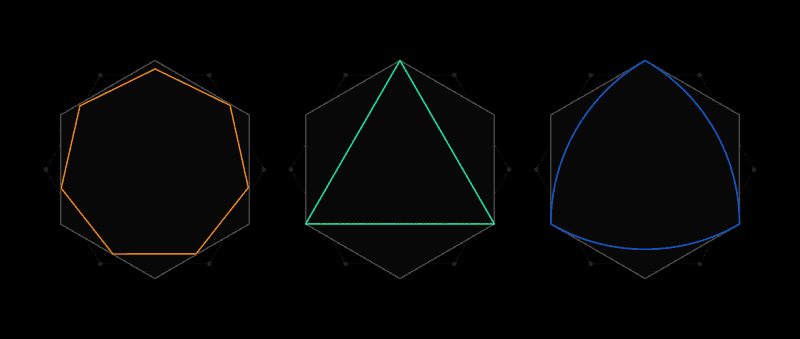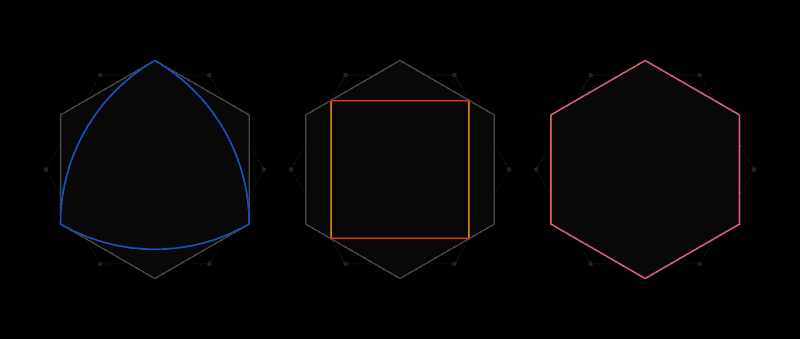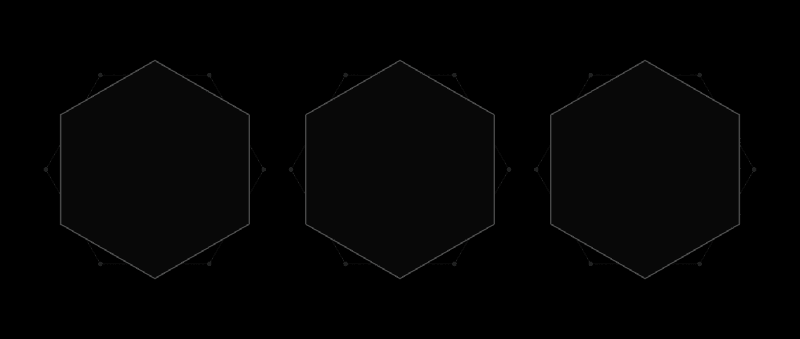
Such a universal coating, like a hexagon, can be described around any shape.



Philip Gibbs is not a professional mathematician. So when he wanted to reflect on a task, he was looking for one that an amateur could handle. He discovered a difficult task that can drive even the best minds. And in the work published this year, Gibbs made significant progress in addressing the issue of a century ago, depending on the ability to accurately measure the area down to atomic scales.



The first task was proposed by the French mathematician Henri León Leguegue, in a letter to his friend Julius Pal, written in 1914. Lebesgue asked: what is the shape of the smallest possible area that can fully cover a large number of other forms (having one common property, which is described below)?



Over the past century, the task of searching for universal coverage turned into a mousetrap: progress in solving it, if it happened periodically, has always been amazingly small. Gibbs’s improvement in comparison with this has become cardinal - although you still need to think a little over him.

')

Imagine a dozen paper cuttings of various sizes and shapes lying on your floor. Now imagine that you are offered to come up with another form, large enough to cover any of the existing ones. By experimenting — by applying forms and turning them — you can think of some way to solve this problem. But, having found universal coverage, is it possible to be sure that you have found the smallest? You can imagine that during the day you periodically return to your form, and find the opportunity to cut off additional pieces here and there.



This is the spirit of the Lebesgue task of universal coverage. Instead of paper clippings, it considers forms in which two points of any distance are not further from each other than one unit of length. The most obvious shape will be a circle of diameter 1, but there are an infinite number of them: an equilateral triangle, a regular pentagon, a regular hexagon, a three-sided form with puffy sides, known as the Ryolet triangle - and this is just for starters. A variety of forms makes it difficult to find the smallest coverage of them all.







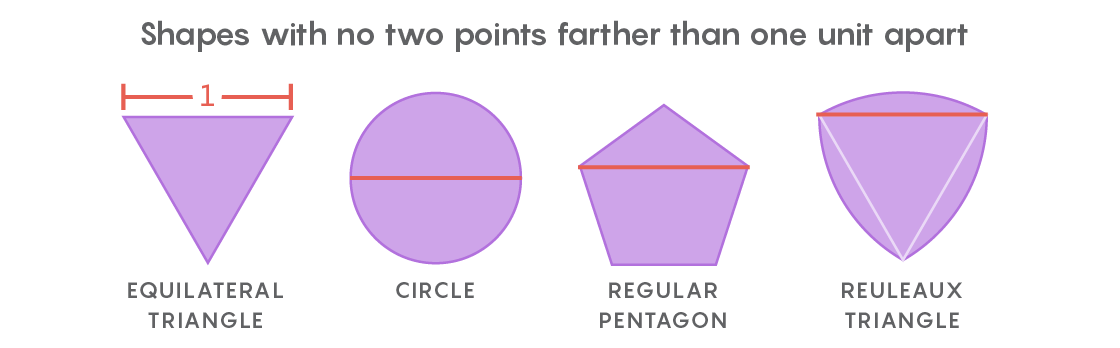
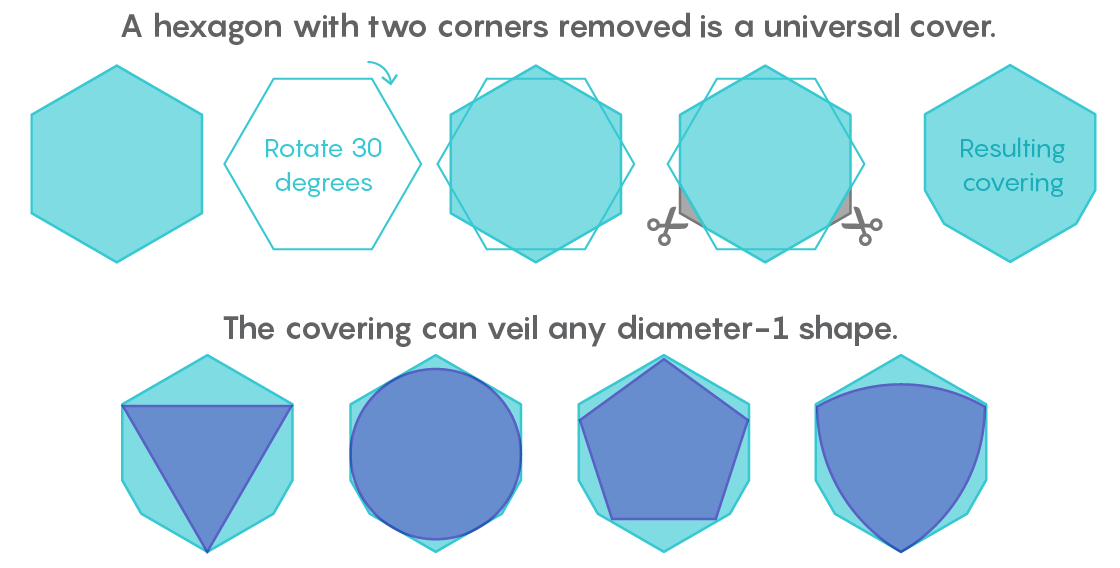
Shortly after receiving a letter from Lebesgue, Pal realized that a universal hexagon would be a universal cover. And then he improved this result, noting that by cutting off the two corners of the hexagon, not standing side by side, you can get a shape with a smaller area, which would still be a universal coating.



“We take a hexagon, put the second one on top of it, rotate it by 30 degrees, and cut off the two corners. At this, Pal finished his research, ”said Gibbs.



In the next 80 years, two other mathematicians cut off narrow strips from Pala’s universal coverage. In 1936, Roland Sprague removed a small piece near one of the corners. In 1992, Hansen would remove two miniature wedges from the bottom right and left corners. Hansen's illustrations could convey the location of these parts, but not their size: their area was 0.00000000004 units.







“You can't draw them on a scale, they would be atom-sized,” said John Baez , a mathematician at the University of California at Riverside.



Baez brought Lebesgue's task out of oblivion when he wrote about it in his blog about popular mathematics in 2013. He admitted that he was fascinated by this task in the way that a video with a sinking insect could enchant you. “My interest in the task was unhealthy,” wrote BAez. - I do not know the reasons for which it may be important. I do not see how it can connect with many other beautiful tasks. It just seems incredibly complex compared to the first impression. I admire people working on it just as I admire people who decided to ski across Antarctica. ”



Philip Gibbs never crossed Antarctica on skis, but read Baez’s blog. When he met a record about Lebesgue’s task, he thought: “Here, this is exactly what I need.”

Atomic scissors

Once, Gibbs thought he could become a scientist. He received a degree in mathematics from the University of Cambridge and defended his doctoral degree in theoretical physics at the University of Glasgow. However, he soon lost his enthusiasm for academic research and became a programmer. He worked on systems designed to develop ships, control air traffic and finances, and in 2006 he retired.



Gibbs remained interested in academic issues, but as a non-professional researcher, he could do little. “An independent scientist is hard to keep track of what is happening,” he said. “But if you find the right niche, you can do something and get some useful results.”





Amateur mathematician Philip Gibbs



Such a niche was the Lebesgue problem of universal coverage. This task has never received the attention of mathematicians, so he suspected that he could make some progress. Gibbs also realized that his programming experience could be an advantage. “I always look for tasks that can be solved using computers and experimental mathematics,” he said.



In 2014, Gibbs drove a computer simulation for 200 random shapes of diameter 1. It followed from the simulations that he might be able to cut off a small piece from the top corner of the previous smallest coverage. He turned this into evidence that the new cover would work for all possible shapes of diameter 1. Gibbs sent proof to Baez, who, together with one of his students, Karina Baghdasaryan, helped Gibbs to give the work a formal mathematical style.



The three of them published work on the Internet in February 2015. It reduced the area of ​​the smallest possible universal coverage from 0.8441377 to 0.8441153 units. The savings of 0.0000224 units were almost a million times greater than what Hansen achieved in 1992.



Gibbs was confident that he could improve the result. In a paper published in October, he cut off another relatively large piece of universal coverage, bringing its area to 0.84409359 units.







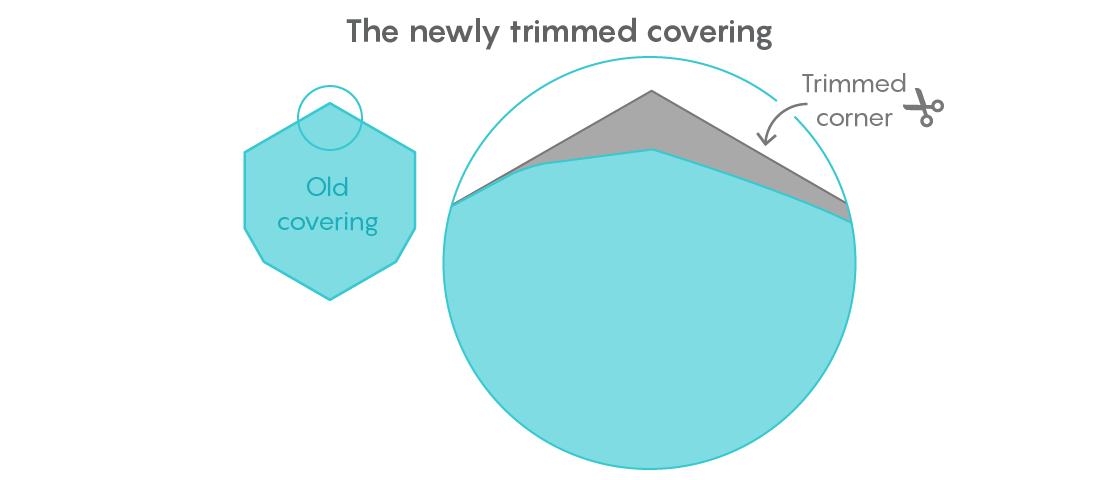
His strategy was to move all the shapes with a diameter of 1 into the corner of the universal cover he had discovered several years ago, and then remove the rest of the area of ​​the opposite angle. But accurate measurement of the area saved was difficult. The techniques used by Gibbs were based on Euclidean geometry, but were performed with such precision that would shock any high school student.



“From the point of view of mathematics, this is all geometry for high school. But performed with fanatical tension, ” wrote Baez.



So far, Gibbs has held the first place in search of the smallest universal coverage, but his prize is in danger. Gibbs believes that there is an opportunity to find coverage even smaller. Baez hopes that the attention that Gibbs returned to the Lebesgue problem stimulates the interest of other mathematicians. Perhaps it is time to put aside the ruler and compass and use the whole arsenal of modern mathematics.



“It is possible that a completely different way will be used to solve this riddle,” he said, “although I have no idea what ideas it may be.”