Mixture Density Networks
Hello!
Let's talk about, as you probably already guessed, neural networks and machine learning. From the title it is clear that Mixture Density Networks will be discussed, then simply MDN, I don’t want to translate the name and leave it as it is. Yes, yes, yes ... there will be some boring mathematics and probability theory, but without it, unfortunately, or fortunately, then decide for yourself, it is difficult to imagine the world of machine learning. But I hasten to reassure you, it will be relatively small and it will not be very difficult. And in general it will be possible to skip it, but just look at a small amount of code in Python and PyTorch, that's right, we will write the network using PyTorch, as well as various graphs with results. But the most important thing is that there will be an opportunity to understand a bit and understand what the MD network is.
Well, let's start!
Regression
Let's first refresh our knowledge a little and remember, quite briefly, what linear regression is .
')
We have a vector X = \ {x_1, x_2, ..., x_n \} we need to predict the value which somehow depends on using a certain linear model:
As the error function, we will use the standard deviation (Squared Error):
This problem can be solved directly by taking the derivative of SE and equating its value to zero:
Thus, we simply find its minimum, and the SE is a quadratic function, so the minimum will always exist. After that, you can already easily find :
That's all, the problem is solved. At the end we’ll remember what linear regression is.
Of course, the dependence inherent in the nature of data generation may be different and then we need to add some nonlinearity to our model. Solving the regression problem directly for big and real data is also a bad idea, since there is a matrix there dimensions , and it is still necessary to find its inverse matrix, and it often happens that such a matrix simply does not exist. In this case, various methods based on gradient descent come to our rescue. And non-linearity of models can be implemented in different ways, including using neural networks.
But now, let's talk not about this, but about the error functions. What is the difference between SE and Log-Likelihood in the case where the data may have a non-linear relationship?
We deal with the zoo, namely: OLS, LS, SE, MSE, RSS
All this is essentially the same, RSS is the residual sum of squares, OLS is the least squares, LS is the least squares, MSE is the mean squared error, SE is squared error. In different sources you can find different names. The essence of this is only one: the square deviation . You can get confused of course, but you get used to it quickly.
It is worth noting that MSE is the standard deviation, a kind of mean error for the entire training data set. In practice, MSE is usually used. The formula is no different:
It is worth noting that MSE is the standard deviation, a kind of mean error for the entire training data set. In practice, MSE is usually used. The formula is no different:
- dataset size, - model prediction for .
Stop! Likelihood? This is something from probability theory. That's right - this is the theory of probability in its purest form. But how can the standard deviation be related to the likelihood function? And as it turns out connected. Associated with finding the maximum likelihood (Maximum Likelihood) and with the normal distribution, to be more precise, with its average .
In order to realize that this is the case, let’s look again at the square deviation function:
Now suppose that the likelihood function has a normal appearance, that is, a Gaussian or normal distribution:
In general, what is the likelihood function and what meaning it contains I will not tell, you can read about this in another place, you should also get acquainted with the concept of conditional probability, Bayes theorem and much more, for a deeper understanding. It all goes into pure probability theory, which is studied both at school and at university.
Now, remembering the normal distribution formula, we get:
And what if we put the standard deviation and remove all the constants in the formula (2), just remove it, do not reduce, because finding the minimum of the function does not depend on them. Then see this:
Still nothing like? Not? Well, what if we take the logarithm of the function? From the logarithm there are generally some pluses: multiplication will transform into a sum, degree into multiplication, and - for this property it is worth clarifying that this is a natural logarithm and strictly speaking . And in general, the logarithm of a function does not change its maximum, and this is the main feature for us. About the connection with Log-Likelihood and Likelihood and why it will be useful to be discussed below, in a small digression. And so, what we did: removed all the constants, and took the logarithm of the likelihood function. They also removed the minus sign, thus turning the Log-Likelihood into the Negative Log-Likelihood (NLL), the connection between them will also be described as a bonus. As a result, we got the NLL function:
Take another look at the RSS (1) function. Yes, they are the same! Exactly! It also shows that .
If we use the MSE standard deviation function, we get from this:
Where - expected value, - the parameters of the model, we will further denote them as: .
Conclusion: If, in the regression question, we use the LS family as error functions, then in essence we solve the problem of finding the maximum likelihood function in the case when the distribution is Gaussian. And the predicted value equal to the average in the normal distribution. And now we know how all this is connected, how probability theory is related (with its likelihood function and normal distribution) and the methods of standard deviation or OLS. More details about this can be found in [2].
And here is the promised bonus. If we are talking about the links between the various functions of the error, we consider (not necessarily to read):
Relationship between Cross-Entropy, Likelihood, Log-Likelihood and Negative Log-Likelihood
Suppose we have data X = \ {x_1, x_2, x_3, x_4, ... \} , each point belongs to a certain class, for example \ {x_1 \ rightarrow1, x_2 \ rightarrow2, x_3 \ rightarrow n, ... \} . There is a total classes, with class 1 occurring time class 2 - time and class - time. We have trained some model on this data. . The likelihood function for it will look like this:
Where - predicted probability for a class .
Take the logarithm of the likelihood function and get the Log-Likelihood:
Example. Consider a binary classification. We have class values:
Real probability for class 0 equals for class 1 equals . Suppose we have a binary classifier that predicts the probability of class 0 for each example, respectively, for class 1, the probability is . We plot the values of the Log-Loss function for different predictions. :
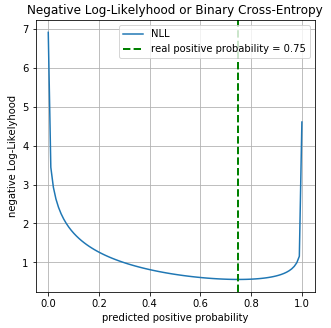
On the graph you can see that the minimum of the Log-Loss function corresponds to the point 0.75, i.e. if our model had completely “learned” the distribution of the source data, .
Where - predicted probability for a class .
Take the logarithm of the likelihood function and get the Log-Likelihood:
Probability lies in the range from 0 to 1, based on the definition of probability. Therefore, the logarithm will be negative. And if you multiply the Log-Likelihood by -1, we get the Negative Log-Likelihood (NLL) function:
If we divide NLL by the number of points in , , we get:
however, you can see that the real probability for the class equals: . From here we get:
Now if you look at the definition of cross-entropy then we get:
In the case when we have only two classes (binary classification) we get the formula for binary cross entropy (you can also meet the well-known name Log-Loss):
From all this, it can be understood that in some cases, minimizing Cross-Entropy is equivalent to minimizing NLL or finding the maximum likelihood function (Likelihood) or Log-Likelihood.
Example. Consider a binary classification. We have class values:
y = np.array([0, 1, 1, 1, 1, 0, 1, 1]).astype(np.float32) Real probability for class 0 equals for class 1 equals . Suppose we have a binary classifier that predicts the probability of class 0 for each example, respectively, for class 1, the probability is . We plot the values of the Log-Loss function for different predictions. :

On the graph you can see that the minimum of the Log-Loss function corresponds to the point 0.75, i.e. if our model had completely “learned” the distribution of the source data, .
Regression using neural networks
Here we come to the more interesting, to practice. Let's see how you can solve the regression problem using neural networks (neural networks). We will implement everything in the Python programming language; to create a network, we use the PyTorch deep learning library.
Source data generation
Input data we will generate using uniform distribution (uniform distribution), we will take an interval from-15 to 15, . Points get using the equation:
Where - vector of noise dimension obtained using the normal distribution with parameters: .
Data generation
N = 3000 # IN_DIM = 1 OUT_DIM = IN_DIM x = np.random.uniform(-15., 15., (IN_DIM, N)).T.astype(np.float32) noise = np.random.normal(size=(N, 1)).astype(np.float32) y = 0.5*x+ 8.*np.sin(0.3*x) + noise # 3 x_train, x_test, y_train, y_test = train_test_split(x, y) # 
Graph of the data.
Network building
Create a regular forward distribution network (feed forward neural network or FFNN).
Build FFNN
class Net(nn.Module): def __init__(self, input_dim=IN_DIM, out_dim=OUT_DIM, layer_size=40): super(Net, self).__init__() self.fc = nn.Linear(input_dim, layer_size) self.logit = nn.Linear(layer_size, out_dim) def forward(self, x): x = F.tanh(self.fc(x)) # 4 x = self.logit(x) return x Our network consists of one hidden layer with the dimension of 40 neurons and with the activation function - hyperbolic tangent:
The output layer is an ordinary linear transformation without an activation function.
Training and getting results
We’ll use AdamOptimizer as an optimizer. Number of learning epochs = 2000, learning rate (learning rate or lr) = 0.1.
FFNN training
def train(net, x_train, y_train, x_test, y_test, epoches=2000, lr=0.1): criterion = nn.MSELoss() optimizer = optim.Adam(net.parameters(), lr=lr) N_EPOCHES = epoches BS = 1500 n_batches = int(np.ceil(x_train.shape[0] / BS)) train_losses = [] test_losses = [] for i in range(N_EPOCHES): for bi in range(n_batches): x_batch, y_batch = fetch_batch(x_train, y_train, bi, BS) x_train_var = Variable(torch.from_numpy(x_batch)) y_train_var = Variable(torch.from_numpy(y_batch)) optimizer.zero_grad() outputs = net(x_train_var) loss = criterion(outputs, y_train_var) loss.backward() optimizer.step() with torch.no_grad(): x_test_var = Variable(torch.from_numpy(x_test)) y_test_var = Variable(torch.from_numpy(y_test)) outputs = net(x_test_var) test_loss = criterion(outputs, y_test_var) test_losses.append(test_loss.item()) train_losses.append(loss.item()) if i%100 == 0: sys.stdout.write('\r Iter: %d, test loss: %.5f, train loss: %.5f' %(i, test_loss.item(), loss.item())) sys.stdout.flush() return train_losses, test_losses net = Net() train_losses, test_losses = train(net, x_train, y_train, x_test, y_test) Now look at the learning outcomes.
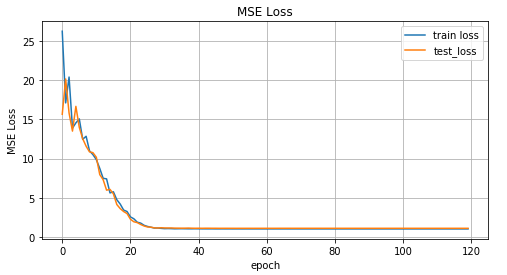
The graph of the MSE function values versus the learning iteration, the graph of the values for the training data and the test data.
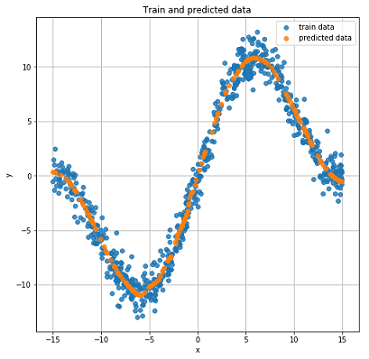
Real and predicted results on test data.
Inverted data
Complicate the task and invert the data.
Invert data
x_train_inv = y_train y_train_inv = x_train x_test_inv = y_train y_test_inv = x_train 
Graph Inverted data.
To predict let's use the direct distribution network from the previous section and see how it handles it.
inv_train_losses, inv_test_losses = train(net, x_train_inv, y_train_inv, x_test_inv, y_test_inv) 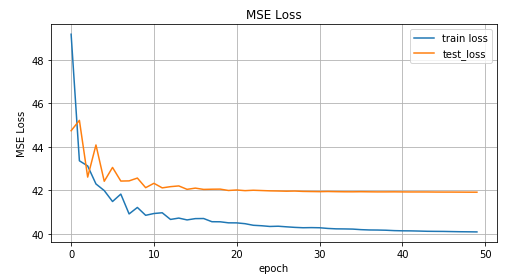
The graph of the MSE function values versus the learning iteration, the graph of the values for the training data and the test data.
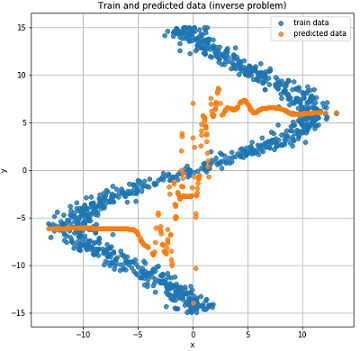
Real and predicted results on test data.
As you can see from the graphs above, our network did n’t cope at all with such data; it simply cannot predict them. And all this happened because in such an inverted task for one point several points can match . You ask, what about noise? He, too, created a situation in which for one could get multiple values . Yes, it's true. But the thing is that, despite the noise, it was all one definite distribution. And since our model essentially predicted , and in the case of MSE, this was the average value for a normal distribution (why this is explained in the first part of the article), then it coped well with the “direct” task. In the opposite case, we get several different distributions for one and accordingly we can not get a good result using only one normal distribution.
Mixture Density Network
The fun begins! What is the Mixture Density Network (further MDN or MD network)? In general, this kind of model that is able to simulate several distributions at once:
What an incomprehensible formula, you say. Let's see. Our MD network is learning to model the average. and variance for several distributions. In the formula (5) - the so-called significance coefficients of the individual distribution for each point , a certain mixing coefficient or how much each of the distributions contributes to a certain point. There is a total distributions.
Just a couple of words about - in fact, this is also a distribution and represents the probability that for a point there will be a condition .
Fuh, again this mathematics, let's write something already. And so, let's start implementing the network. For our network, take .
self.fc = nn.Linear(input_dim, layer_size) self.fc2 = nn.Linear(layer_size, 50) self.pi = nn.Linear(layer_size, coefs) self.mu = nn.Linear(layer_size, out_dim*coefs) # mean self.sigma_sq = nn.Linear(layer_size, coefs) # variance Define the output layers for our network:
x = F.relu(self.fc(x)) x = F.relu(self.fc2(x)) pi = F.softmax(self.pi(x), dim=1) sigma_sq = torch.exp(self.sigma_sq(x)) mu = self.mu(x) Write the error function or loss function, formula (5):
def gaussian_pdf(x, mu, sigma_sq): return (1/torch.sqrt(2*np.pi*sigma_sq)) * torch.exp((-1/(2*sigma_sq)) * torch.norm((x-mu), 2, 1)**2) losses = Variable(torch.zeros(y.shape[0])) # p(y|x) for i in range(COEFS): likelihood = gaussian_pdf(y, mu[:, i*OUT_DIM:(i+1)*OUT_DIM], sigma_sq[:, i]) prior = pi[:, i] losses += prior * likelihood loss = torch.mean(-torch.log(losses)) Full MDN Build Code
COEFS = 30 class MDN(nn.Module): def __init__(self, input_dim=IN_DIM, out_dim=OUT_DIM, layer_size=50, coefs=COEFS): super(MDN, self).__init__() self.fc = nn.Linear(input_dim, layer_size) self.fc2 = nn.Linear(layer_size, 50) self.pi = nn.Linear(layer_size, coefs) self.mu = nn.Linear(layer_size, out_dim*coefs) # mean self.sigma_sq = nn.Linear(layer_size, coefs) # variance self.out_dim = out_dim self.coefs = coefs def forward(self, x): x = F.relu(self.fc(x)) x = F.relu(self.fc2(x)) pi = F.softmax(self.pi(x), dim=1) sigma_sq = torch.exp(self.sigma_sq(x)) mu = self.mu(x) return pi, mu, sigma_sq # def gaussian_pdf(x, mu, sigma_sq): return (1/torch.sqrt(2*np.pi*sigma_sq)) * torch.exp((-1/(2*sigma_sq)) * torch.norm((x-mu), 2, 1)**2) # def loss_fn(y, pi, mu, sigma_sq): losses = Variable(torch.zeros(y.shape[0])) # p(y|x) for i in range(COEFS): likelihood = gaussian_pdf(y, mu[:, i*OUT_DIM:(i+1)*OUT_DIM], sigma_sq[:, i]) prior = pi[:, i] losses += prior * likelihood loss = torch.mean(-torch.log(losses)) return loss Our MD network is ready to go. Almost ready. It remains to train her and look at the results.
MDN Training
def train_mdn(net, x_train, y_train, x_test, y_test, epoches=1000): optimizer = optim.Adam(net.parameters(), lr=0.01) N_EPOCHES = epoches BS = 1500 n_batches = int(np.ceil(x_train.shape[0] / BS)) train_losses = [] test_losses = [] for i in range(N_EPOCHES): for bi in range(n_batches): x_batch, y_batch = fetch_batch(x_train, y_train, bi, BS) x_train_var = Variable(torch.from_numpy(x_batch)) y_train_var = Variable(torch.from_numpy(y_batch)) optimizer.zero_grad() pi, mu, sigma_sq = net(x_train_var) loss = loss_fn(y_train_var, pi, mu, sigma_sq) loss.backward() optimizer.step() with torch.no_grad(): if i%10 == 0: x_test_var = Variable(torch.from_numpy(x_test)) y_test_var = Variable(torch.from_numpy(y_test)) pi, mu, sigma_sq = net(x_test_var) test_loss = loss_fn(y_test_var, pi, mu, sigma_sq) train_losses.append(loss.item()) test_losses.append(test_loss.item()) sys.stdout.write('\r Iter: %d, test loss: %.5f, train loss: %.5f' %(i, test_loss.item(), loss.item())) sys.stdout.flush() return train_losses, test_losses mdn_net = MDN() mdn_train_losses, mdn_test_losses = train_mdn(mdn_net, x_train_inv, y_train_inv, x_test_inv, y_test_inv) 
Graph of values of loss function depending on the iteration of training, on the graph of the values for the training data and test data.
Since our network has learned the mean values for several distributions, let's look at it:
pi, mu, sigma_sq = mdn_net(Variable(torch.from_numpy(x_test_inv))) 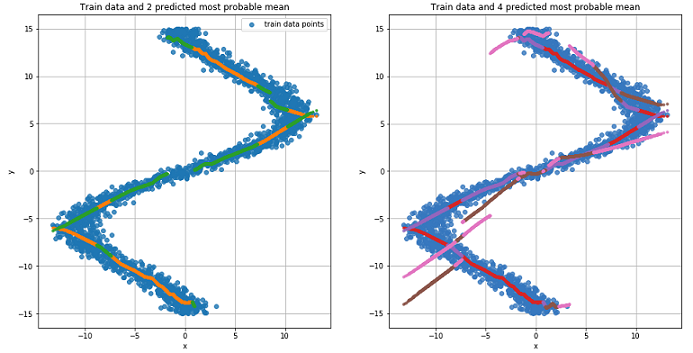
Chart for the two most likely mean values for each point (left). Chart for the 4 most likely mean values for each point (right).
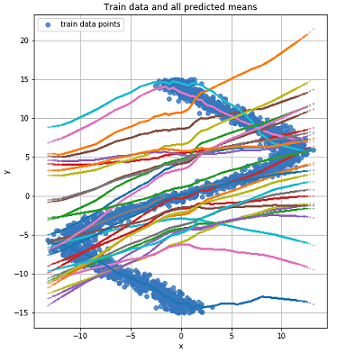
Graph for all mean values for each point.
To predict the data, we will randomly choose several values. and based on the value . And then based on them generate target data using normal distribution.
Result prediction
def rand_n_sample_cumulative(pi, mu, sigmasq, samples=10): n = pi.shape[0] out = Variable(torch.zeros(n, samples, OUT_DIM)) for i in range(n): for j in range(samples): u = np.random.uniform() prob_sum = 0 for k in range(COEFS): prob_sum += pi.data[i, k] if u < prob_sum: for od in range(OUT_DIM): sample = np.random.normal(mu.data[i, k*OUT_DIM+od], np.sqrt(sigmasq.data[i, k])) out[i, j, od] = sample break return out pi, mu, sigma_sq = mdn_net(Variable(torch.from_numpy(x_test_inv))) preds = rand_n_sample_cumulative(pi, mu, sigma_sq, samples=10) 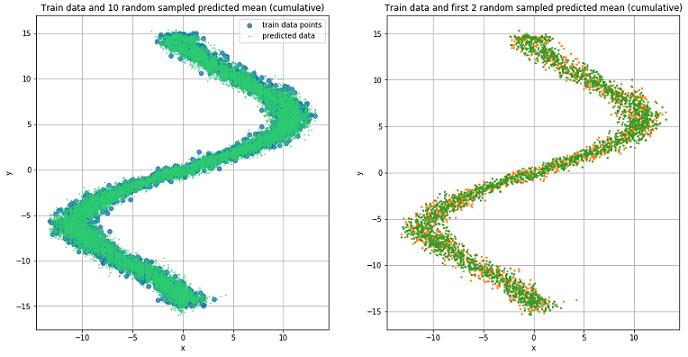
Predicted data for 10 randomly selected values. and (left) and two (right).
From the figures it is clear that MDN did an excellent job with the “reverse” task.
Using more complex data
Let's see how our MD network will cope with more complex data, such as spiral data. The equation of a hyperbolic spiral in Cartesian coordinates:
Spiral Data Generation
N = 2000 x_train_compl = [] y_train_compl = [] x_test_compl = [] y_test_compl = [] noise_train = np.random.uniform(-1, 1, (N, IN_DIM)).astype(np.float32) noise_test = np.random.uniform(-1, 1, (N, IN_DIM)).astype(np.float32) for i, theta in enumerate(np.linspace(0, 5*np.pi, N).astype(np.float32)): # 6 r = ((theta)) x_train_compl.append(r*np.cos(theta) + noise_train[i]) y_train_compl.append(r*np.sin(theta)) x_test_compl.append(r*np.cos(theta) + noise_test[i]) y_test_compl.append(r*np.sin(theta)) x_train_compl = np.array(x_train_compl).reshape((-1, 1)) y_train_compl = np.array(y_train_compl).reshape((-1, 1)) x_test_compl = np.array(x_test_compl).reshape((-1, 1)) y_test_compl = np.array(y_test_compl).reshape((-1, 1)) 
Graph of the obtained spiral data.
For the sake of interest, let's see how a regular Feed-Forward network will cope with this task.
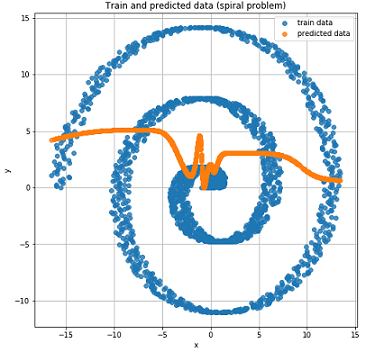
As expected, the Feed-Forward network is unable to solve the regression problem for such data.
We use the previously described and created MD network for training on spiral data.
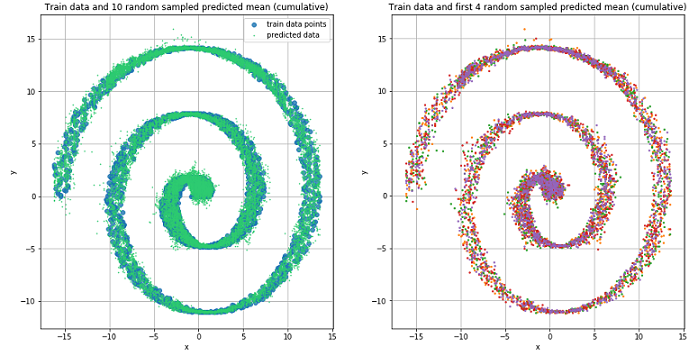
Mixture Density Network did a great job in this situation.
Conclusion
At the beginning of this article, we recalled the basics of linear regression. Saw that the general between finding of average for normal distribution and MSE. Disassembled as connected NLL and cross entropy. And most importantly, we figured out the MDN model, which is capable of learning from data obtained from a mixed distribution. I hope the article was clear and interesting, despite the fact that there was a bit of mathematics.
The full code can be viewed on GitHub .
Literature
Source: https://habr.com/ru/post/433804/
All Articles