The amazing performance of parallel C ++ 17 algorithms. Myth or Reality?
Good evening!
From our course “Developer C ++” we offer you a small and interesting study about parallel algorithms.
Go.
')
With the advent of parallel algorithms in C ++ 17, you can easily update your “computational” code and benefit from parallel execution. In this article, I want to consider the STL algorithm, which naturally reveals the idea of independent computing. Is it possible to expect 10-fold acceleration with a 10-core processor? Maybe more? Or less? Let's talk about it.
Introduction to parallel algorithms

C ++ 17 offers an execution policy option for most algorithms:
Briefly:
As a quick example, we call
Note how easy it is to add a parallel execution parameter to the algorithm! But will it be possible to achieve significant performance improvements? Will it increase the speed? Or are there cases of slowdown?
Parallel
In this article, I want to draw attention to the
Our test code will be based on the following pattern:
Suppose that the
I would like to experiment with the following things:
As you can see, I want to not only test the number of elements that are “good” for using the parallel algorithm, but also the ALU operations that the processor occupies.
Other algorithms, such as sorting, accumulation (in the form of std :: reduce) also offer parallel execution, but also require more work to calculate the results. Therefore, we will consider them candidates for another article.
Benchmark Note
For my tests, I use Visual Studio 2017, 15.8 - since this is the only implementation in the popular / STL compiler implementation at the current time (November, 2018) (GCC on the way!). Moreover, I focused only on
There are two computers:
The code is compiled into x64, Release more, auto-vectorization is enabled by default, I also included the extended command set (SSE2) and OpenMP (2.0).
The code is in my github: github / fenbf / ParSTLTests / TransformTests / TransformTests.cpp
For OpenMP (2.0), I use parallelism only for loops:
I run the code 5 times and look at the minimum results.
Warning : The results reflect only rough observations, check on your system / configuration before using in production. Your requirements and environment may differ from mine.
More details about MSVC implementation can be found in this post . But the latest report of Bill O'Neal with CppCon 2018 (Bill implemented Parallel STL in MSVC).
Well, let's start with simple examples!
Simple conversion
Consider the case when you apply a very simple operation to the input vector. This may be copying or multiplying elements.
For example:
My computer has 6 or 4 cores ... can I expect a 4..6-fold acceleration of sequential execution? Here are my results (time in milliseconds):
On a faster machine, we can see that it will take about 1 million items to notice an improvement in performance. On the other hand, on my laptop all parallel implementations were slower.
Thus, it is difficult to notice any significant performance improvement with such transformations, even with an increase in the number of elements.
Why so?
Since the operations are elementary, the processor cores can call it almost instantly, using only a few cycles. However, the processor cores spend more time waiting for the main memory. So, in this case, for the most part they will wait, rather than perform calculations.
Reading and writing a variable in memory takes about 2-3 clocks if it is cached, and a few hundred clocks if not cached.
https://www.agner.org/optimize/optimizing_cpp.pdf
You can roughly say that if your algorithm depends on memory, then you should not expect an improvement in performance with parallel computation.
More calculations
Because memory bandwidth is extremely important and can affect the speed of things ... let's increase the number of calculations affecting each element.
The idea is that it is better to use processor cycles, and not to waste time waiting for memory.
To begin with, I use trigonometric functions, for example,
We use
For more information about the delays of the teams, see the excellent Perf Guide article from Agner Fogh .
Here is the benchmark code:
And now what? Can we expect to improve performance compared to the previous attempt?
Here are some results (time in milliseconds):
Finally, we see quite good numbers :)
For 1000 elements (not shown here), the time for parallel and sequential calculations was similar, so for more than 1000 elements we see an improvement in the parallel version.
For 100 thousand items, the result on a faster computer is almost 9 times better than the sequential version (similarly for the OpenMP version).
In the largest variant of a million elements - the result is faster by 5 or 8 times.
For such calculations, I achieved “linear” acceleration, depending on the number of processor cores. What was expected.
Fresnel and 3D Vectors
In the section above, I used “made-up” calculations, but what about the real code?
Let's solve the Fresnel equations that describe the reflection and curvature of light from a smooth, flat surface. This is a popular method for generating realistic lighting in 3D games.
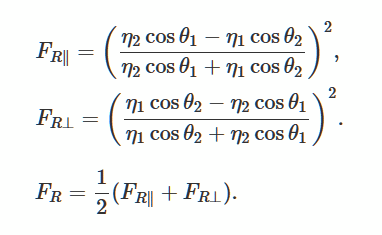

Photo from Wikimedia
As a good sample, I found this description and implementation .
About using the GLM library
Instead of creating my own implementation, I used the glm library . I often use it in my OpenGl projects.
The library is easy to access through the Conan Package Manager , so I will use it too. Link to package.
Conan file:
and the command line to install the library (it generates props files that I can use in the Visual Studio project):
The library consists of a header, so you can simply download it manually if you want.
Actual code and benchmark
I adapted the glm code from scratchapixel.com :
The code uses several mathematical instructions, scalar product, multiplication, division, so the processor has something to do. Instead of the double vector, we use a vector of 4 elements to increase the amount of used memory.
Benchmark:
And here are the results (time in milliseconds):
With “real” computations, we see that parallel algorithms provide good performance. For such operations on two of my Windows machines, I achieved acceleration with an almost linear dependence on the number of cores.
For all tests, I also showed results from OpenMP and two implementations: MSVC and OpenMP work in a similar way.
Conclusion
In this article, I examined three cases of the use of parallel computing and parallel algorithms. Replacing the standard algorithms with the version of std :: execution :: par may seem very tempting, but this is not always worth it! Each operation you use inside the algorithm may work differently and be more dependent on the processor or memory. Therefore, consider each change separately.
What is worth remembering:
Special thanks to JFT for helping with the article!
Also note my other sources about parallel algorithms:
Check out another article related to Parallel Algorithms: How to Boost Performance with Intel Parallel STL and C ++ 17 Parallel Algorithms
THE END
We are waiting for comments and questions that can be left here or with our teacher at the open door .
From our course “Developer C ++” we offer you a small and interesting study about parallel algorithms.
Go.
')
With the advent of parallel algorithms in C ++ 17, you can easily update your “computational” code and benefit from parallel execution. In this article, I want to consider the STL algorithm, which naturally reveals the idea of independent computing. Is it possible to expect 10-fold acceleration with a 10-core processor? Maybe more? Or less? Let's talk about it.
Introduction to parallel algorithms

C ++ 17 offers an execution policy option for most algorithms:
- sequenced_policy is a type of execution policy, is used as a unique type to eliminate the overload of the parallel algorithm and the requirement that parallelization of the execution of a parallel algorithm is impossible: the corresponding global object is
std::execution::seq; - parallel_policy is a type of execution policy used as a unique type to eliminate the overload of the parallel algorithm and to indicate that parallelization of the execution of the parallel algorithm is possible: the corresponding global object is
std::execution::par; - parallel_unsequenced_policy is a type of execution policy used as a unique type for eliminating the overload of the parallel algorithm and indicating that parallelization and vectorization of the parallel algorithm execution are possible: the corresponding global object is
std::execution::par_unseq;
Briefly:
- use
std::execution::seqto execute the algorithm sequentially; - use
std::execution::parto execute the algorithm in parallel (usually with the help of some implementation of the Thread Pool implementation); - use
std::execution::par_unseqfor parallel execution of the algorithm with the possibility of using vector commands (for example, SSE, AVX).
As a quick example, we call
std::sort in parallel: std::sort(std::execution::par, myVec.begin(), myVec.end()); // ^^^^^^^^^^^^^^^^^^^ // Note how easy it is to add a parallel execution parameter to the algorithm! But will it be possible to achieve significant performance improvements? Will it increase the speed? Or are there cases of slowdown?
Parallel
std::transformIn this article, I want to draw attention to the
std::transform algorithm, which can potentially be the basis for other parallel methods (along with std::transform_reduce , for_each , scan , sort ...).Our test code will be based on the following pattern:
std::transform(execution_policy, // par, seq, par_unseq inVec.begin(), inVec.end(), outVec.begin(), ElementOperation); Suppose that the
ElementOperation function ElementOperation not have any synchronization methods, in which case the code has the potential for parallel execution or even vectorization. Each element calculation is independent, the order does not matter, so the implementation can generate several threads (possibly in a thread pool) for independent processing of elements.I would like to experiment with the following things:
- the size of the vector field is large or small;
- a simple conversion that spends most of the time accessing memory;
- more arithmetic (ALU) operations;
- ALU in a more realistic scenario.
As you can see, I want to not only test the number of elements that are “good” for using the parallel algorithm, but also the ALU operations that the processor occupies.
Other algorithms, such as sorting, accumulation (in the form of std :: reduce) also offer parallel execution, but also require more work to calculate the results. Therefore, we will consider them candidates for another article.
Benchmark Note
For my tests, I use Visual Studio 2017, 15.8 - since this is the only implementation in the popular / STL compiler implementation at the current time (November, 2018) (GCC on the way!). Moreover, I focused only on
execution::par , since execution::par_unseq not available in MSVC (it works like execution::par ).There are two computers:
- i7 8700 - PC, Windows 10, i7 8700 - clock speed 3.2 GHz, 6 cores / 12 threads (Hyperthreading);
- i7 4720 - Laptop, Windows 10, i7 4720, 2.6GHz clock speed, 4 cores / 8 threads (Hyperthreading).
The code is compiled into x64, Release more, auto-vectorization is enabled by default, I also included the extended command set (SSE2) and OpenMP (2.0).
The code is in my github: github / fenbf / ParSTLTests / TransformTests / TransformTests.cpp
For OpenMP (2.0), I use parallelism only for loops:
#pragma omp parallel for for (int i = 0; ...) I run the code 5 times and look at the minimum results.
Warning : The results reflect only rough observations, check on your system / configuration before using in production. Your requirements and environment may differ from mine.
More details about MSVC implementation can be found in this post . But the latest report of Bill O'Neal with CppCon 2018 (Bill implemented Parallel STL in MSVC).
Well, let's start with simple examples!
Simple conversion
Consider the case when you apply a very simple operation to the input vector. This may be copying or multiplying elements.
For example:
std::transform(std::execution::par, vec.begin(), vec.end(), out.begin(), [](double v) { return v * 2.0; } ); My computer has 6 or 4 cores ... can I expect a 4..6-fold acceleration of sequential execution? Here are my results (time in milliseconds):
| Operation | Vector size | i7 4720 (4 cores) | i7 8700 (6 cores) |
|---|---|---|---|
| execution :: seq | 10k | 0.002763 | 0.001924 |
| execution :: par | 10k | 0.009869 | 0.008983 |
| openmp parallel for | 10k | 0.003158 | 0.002246 |
| execution :: seq | 100k | 0.051318 | 0.028872 |
| execution :: par | 100k | 0.043028 | 0.025664 |
| openmp parallel for | 100k | 0.022501 | 0.009624 |
| execution :: seq | 1000k | 1.69508 | 0.52419 |
| execution :: par | 1000k | 1.65561 | 0.359619 |
| openmp parallel for | 1000k | 1.50678 | 0.344863 |
On a faster machine, we can see that it will take about 1 million items to notice an improvement in performance. On the other hand, on my laptop all parallel implementations were slower.
Thus, it is difficult to notice any significant performance improvement with such transformations, even with an increase in the number of elements.
Why so?
Since the operations are elementary, the processor cores can call it almost instantly, using only a few cycles. However, the processor cores spend more time waiting for the main memory. So, in this case, for the most part they will wait, rather than perform calculations.
Reading and writing a variable in memory takes about 2-3 clocks if it is cached, and a few hundred clocks if not cached.
https://www.agner.org/optimize/optimizing_cpp.pdf
You can roughly say that if your algorithm depends on memory, then you should not expect an improvement in performance with parallel computation.
More calculations
Because memory bandwidth is extremely important and can affect the speed of things ... let's increase the number of calculations affecting each element.
The idea is that it is better to use processor cycles, and not to waste time waiting for memory.
To begin with, I use trigonometric functions, for example,
sqrt(sin*cos) (these are conditional calculations in a non-optimal form, just to occupy the processor).We use
sqrt , sin and cos , which can take ~ 20 per sqrt and ~ 100 per trigonometric function. This amount of computation can cover the memory access delay.For more information about the delays of the teams, see the excellent Perf Guide article from Agner Fogh .
Here is the benchmark code:
std::transform(std::execution::par, vec.begin(), vec.end(), out.begin(), [](double v) { return std::sqrt(std::sin(v)*std::cos(v)); } ); And now what? Can we expect to improve performance compared to the previous attempt?
Here are some results (time in milliseconds):
| Operation | Vector size | i7 4720 (4 cores) | i7 8700 (6 cores) |
|---|---|---|---|
| execution :: seq | 10k | 0.105005 | 0.070577 |
| execution :: par | 10k | 0.055661 | 0.03176 |
| openmp parallel for | 10k | 0.096321 | 0.024702 |
| execution :: seq | 100k | 1.08755 | 0.707048 |
| execution :: par | 100k | 0.259354 | 0.17195 |
| openmp parallel for | 100k | 0.898465 | 0.189915 |
| execution :: seq | 1000k | 10.5159 | 7.16254 |
| execution :: par | 1000k | 2.44472 | 1.10099 |
| openmp parallel for | 1000k | 4.78681 | 1.89017 |
Finally, we see quite good numbers :)
For 1000 elements (not shown here), the time for parallel and sequential calculations was similar, so for more than 1000 elements we see an improvement in the parallel version.
For 100 thousand items, the result on a faster computer is almost 9 times better than the sequential version (similarly for the OpenMP version).
In the largest variant of a million elements - the result is faster by 5 or 8 times.
For such calculations, I achieved “linear” acceleration, depending on the number of processor cores. What was expected.
Fresnel and 3D Vectors
In the section above, I used “made-up” calculations, but what about the real code?
Let's solve the Fresnel equations that describe the reflection and curvature of light from a smooth, flat surface. This is a popular method for generating realistic lighting in 3D games.
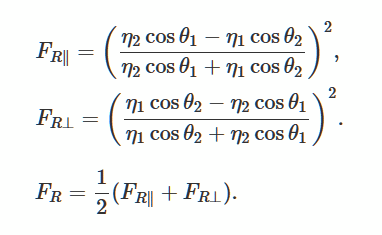

Photo from Wikimedia
As a good sample, I found this description and implementation .
About using the GLM library
Instead of creating my own implementation, I used the glm library . I often use it in my OpenGl projects.
The library is easy to access through the Conan Package Manager , so I will use it too. Link to package.
Conan file:
[requires] glm/0.9.9.1@g-truc/stable [generators] visual_studio and the command line to install the library (it generates props files that I can use in the Visual Studio project):
conan install . -s build_type=Release -if build_release_x64 -s arch=x86_64 The library consists of a header, so you can simply download it manually if you want.
Actual code and benchmark
I adapted the glm code from scratchapixel.com :
// https://www.scratchapixel.com float fresnel(const glm::vec4 &I, const glm::vec4 &N, const float ior) { float cosi = std::clamp(glm::dot(I, N), -1.0f, 1.0f); float etai = 1, etat = ior; if (cosi > 0) { std::swap(etai, etat); } // sini float sint = etai / etat * sqrtf(std::max(0.f, 1 - cosi * cosi)); // if (sint >= 1) return 1.0f; float cost = sqrtf(std::max(0.f, 1 - sint * sint)); cosi = fabsf(cosi); float Rs = ((etat * cosi) - (etai * cost)) / ((etat * cosi) + (etai * cost)); float Rp = ((etai * cosi) - (etat * cost)) / ((etai * cosi) + (etat * cost)); return (Rs * Rs + Rp * Rp) / 2.0f; } The code uses several mathematical instructions, scalar product, multiplication, division, so the processor has something to do. Instead of the double vector, we use a vector of 4 elements to increase the amount of used memory.
Benchmark:
std::transform(std::execution::par, vec.begin(), vec.end(), vecNormals.begin(), // vecFresnelTerms.begin(), // [](const glm::vec4& v, const glm::vec4& n) { return fresnel(v, n, 1.0f); } ); And here are the results (time in milliseconds):
| Operation | Vector size | i7 4720 (4 cores) | i7 8700 (6 cores) |
|---|---|---|---|
| execution :: seq | 1k | 0.032764 | 0.016361 |
| execution :: par | 1k | 0.031186 | 0.028551 |
| openmp parallel for | 1k | 0.005526 | 0.007699 |
| execution :: seq | 10k | 0.246722 | 0.169383 |
| execution :: par | 10k | 0.090794 | 0.067048 |
| openmp parallel for | 10k | 0.049739 | 0.029835 |
| execution :: seq | 100k | 2.49722 | 1.69768 |
| execution :: par | 100k | 0.530157 | 0.283268 |
| openmp parallel for | 100k | 0.495024 | 0.291609 |
| execution :: seq | 1000k | 25.0828 | 16.9457 |
| execution :: par | 1000k | 5.15235 | 2.33768 |
| openmp parallel for | 1000k | 5.11801 | 2.95908 |
With “real” computations, we see that parallel algorithms provide good performance. For such operations on two of my Windows machines, I achieved acceleration with an almost linear dependence on the number of cores.
For all tests, I also showed results from OpenMP and two implementations: MSVC and OpenMP work in a similar way.
Conclusion
In this article, I examined three cases of the use of parallel computing and parallel algorithms. Replacing the standard algorithms with the version of std :: execution :: par may seem very tempting, but this is not always worth it! Each operation you use inside the algorithm may work differently and be more dependent on the processor or memory. Therefore, consider each change separately.
What is worth remembering:
- parallel execution usually does more than sequential, since the library must prepare for parallel execution;
- not only the number of elements is important, but also the number of instructions the processor is occupied with
- it is better to take tasks that are independent of each other and other shared resources;
- parallel algorithms offer an easy way to divide work into separate threads;
- if your operations are memory dependent, you should not expect performance improvements, and in some cases, the algorithms may be slower;
- to get a decent performance improvement, always measure the timings of each problem, in some cases the results may be completely different.
Special thanks to JFT for helping with the article!
Also note my other sources about parallel algorithms:
- A fresh chapter in my book C ++ 17 In Detail on Parallel Algorithms;
- Parallel STL And Filesystem: Files Word Count Example ;
- Examples of parallel algorithms from C ++ 17 .
Check out another article related to Parallel Algorithms: How to Boost Performance with Intel Parallel STL and C ++ 17 Parallel Algorithms
THE END
We are waiting for comments and questions that can be left here or with our teacher at the open door .
Source: https://habr.com/ru/post/433588/
All Articles