AI in the game Hase und Igel: minimax for three

After the real boom of board games of the late 00s, several boxes of games remained in the family. One of them is the game “Rabbit and Hedgehog” in the original German version. A multi-player game in which the element of chance is minimized, and sober calculation and the player’s ability to “look in” several steps ahead conquer.
My frequent defeats in the game led me to the idea of writing a computer “intellect” to select the best move. Intellect, ideally, able to fight with the grandmaster Hare and Hedgehog (and that tea, not chess, the game will be simpler). Further in the article there is a description of the development process, AI logic and a link to the sources.
Game Rules Hare and Yozh
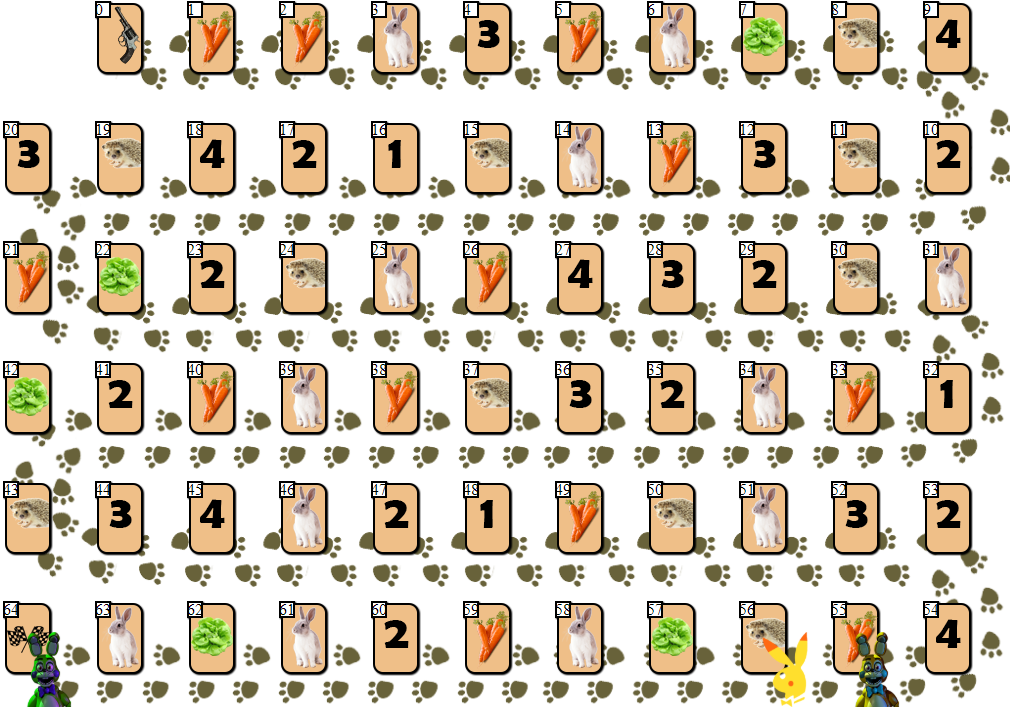
On the playing field in 65 cells, there are several players' chips, from 2 to 6 participants (my drawing, non-canonical, looks, of course, so-so):
')
Apart from the cells with indices 0 (start) and 64 (finish), only one player can be placed in each of the cells. The goal of each player is to move forward to the finish cell, ahead of rivals.
The “fuel” for moving forward is a carrot - a game “ currency ”. At the start, each player receives 68 carrots, which he gives (and sometimes receives) as he moves.
In addition to carrots, the player receives 3 cards of lettuce at the start. Salad is a special “artifact” that a player must get rid of before the finish. Getting rid of the salad (and this can only be done on a special cage of lettuce, like this:

), the player, including, receives additional carrots. Before that, skipping your turn. The more players ahead of the salad leaving the card, the more carrots that player will receive: 10 x (the position of the player on the field relative to other players). That is, the second player on the field will receive 20 carrots, leaving the lettuce cage.
Cells with numbers 1-4 can bring several dozen carrots if the player’s position coincides with the number on the cage (1-4, cage number 1 is also suitable for the 4th and 6th positions on the field), by analogy with the lettuce cage.
The player can skip the move, remaining on the cage with the image of carrots and get or give for this action 10 carrots. Why should a player give “fuel”? The fact is that a player can only finish having 10 carrots after his final move (20 if you finish second, 30 if third, etc.).
Finally, a player can get 10 x N carrots by making N steps on the nearest free hedgehog (if the nearest hedgehog is busy, such a move is impossible).
The cost of moving forward is calculated not proportionally to the number of moves, according to the formula (rounded up):
,
where N is the number of steps forward.
So for a step forward one cell, the player gives 1 carrot, 3 carrots for 2 cells, 6 carrots for 3 cells, 10 for 4, ..., 210 carrots for moving 20 cells forward.
The last cage, the hare cage, introduces an element of randomness into the game. When a player gets into a cage with a hare, he pulls a special card from the pile, after which some action is taken. Depending on the card and the game situation, the player may lose some carrots, get extra carrots, or skip one turn. It should be noted that among the cards with “effects” there are several more negative scenarios for the player, which encourages the game to be cautious and calculated.
No AI implementation
In the very first implementation, which will then become the basis for the development of the game “intellect”, I have limited myself to the option in which each move is made by a player - a person.
I decided to implement the game as a client - a static one-page website, all of the “logic” of which is implemented on JS and the server is a WEB API application. The server is written in .NET Core 2.1 and produces at the output one assembly artifact - a dll file that can run under Windows / Linux / Mac OS.
The “logic” of the client part is minimized (just like the UX, since the GUI is purely utilitarian). For example, the web client does not perform the check itself - is the rules requested by the player allowed by the rules? This check is performed on the server. The server also tells the client what moves the player can make from the current playing position.
The server is a classic Moore machine . In the server logic, there are no such concepts as “connected client”, “game session”, etc.
All that the server does is process the received (HTTP POST) command. The “command” pattern is implemented on the server. The client can request the execution of one of the following commands:
- start a new game, i.e. “Arrange” chips of a specified number of players on a “clean” board
- make the move indicated in the team
For the second team, the client sends the current game position to the server (object of Disposition class), that is, a description of the following form:
- position, number of carrots and lettuce for each hare, plus an additional boolean field indicating that the hare is missing its turn
- index hare making a move.
The server does not need to send additional information - for example, information about the playing field. Just as for recording a chess etude, it is not necessary to paint the arrangement of black and white cells on the board - this information is taken as a constant.
In the response, the server indicates whether the command was successful. Technically, a client may, for example, request an invalid move. Or try to create a new game for a single player, which obviously does not make sense.
If the team is successful, the response will contain a new playing position , as well as a list of moves that the next player in the queue (current for the new position) can make.
In addition to this, the server response contains some service fields. For example, the text of the hare card “pulled out” by the player at a step on the corresponding cell.
Player's move
The player's turn is encoded by an integer:
- 0, if the player is forced to stay in the current cell,
1, 2, ... N for 1, ... N steps forward, - -1, -2, ... -M to move 1 ... M cells back to the nearest free hedgehog,
- 1001, 1002 - special codes for the player who decided to stay on the carrot cage and get (1001) or give (1002) 10 carrots for it.
Software implementation
The server receives the JSON of the requested command, parses it into one of the corresponding request classes, and performs the requested action.
If the client (player) requested to make a move with the CMD code from the position (POS) transferred to the team, the server performs the following actions:
- checks if such a move is possible
- creates a new position from the current one, applying corresponding modifications to it,
gets many possible moves for a new position. Let me remind you that the index of the player making the move is already included in the object describing the position , - returns a response to the client with a new position, possible moves, or the success flag equal to false, and a description of the error.
The logic of checking the admissibility of the requested move (CMD) and building a new position turned out to be connected a little more closely than we would like. The search method for permissible moves echoes this logic. All this functionality implements the class TurnChecker.
At the input of the validation / execution method of a turn, TurnChecker obtains an object of a game position class (Disposition). The Disposition object contains an array of player data (Haze [] hazes), the index of the player making a move + some service information that is filled in during the operation of the TurnChecker object.
The game field describes the FieldMap class, which is implemented as a singleton . The class contains an array of cells + some service information used to simplify / speed up subsequent calculations.
Performance considerations
In the implementation of the TurnChecker class, I tried, as far as possible, to avoid cycles. The fact is that the methods for obtaining the set of permissible moves / execution of the course will subsequently be called thousands (tens of thousands) of times during the search procedure for a quasi-optimal move.
So, for example, I calculate how many cells a player can go forward, having N carrots, according to the formula:
When checking if cell i is not occupied by one of the players, I do not run through the list of players (since this action will probably have to be performed many times), but I turn to a dictionary of the form [cell index, busy flag] that was filled in advance.
When checking whether the specified hedgehog cell is the closest (behind) with respect to the current cell occupied by the player, I also compare the requested position with the value from the dictionary of the form [cell_ index, close_back_ index] with static information.
So, for example, I calculate how many cells a player can go forward, having N carrots, according to the formula:
return ((int)Math.Pow(8 * N + 1, 0.5) - 1) / 2; When checking if cell i is not occupied by one of the players, I do not run through the list of players (since this action will probably have to be performed many times), but I turn to a dictionary of the form [cell index, busy flag] that was filled in advance.
When checking whether the specified hedgehog cell is the closest (behind) with respect to the current cell occupied by the player, I also compare the requested position with the value from the dictionary of the form [cell_ index, close_back_ index] with static information.
Implementation with AI
One command is added to the list of commands processed by the server: execute a quasi-optimal, selected by the program, move. This command is a small modification of the “player's move” command, from which the move field ( CMD ) itself is removed.
The first solution that comes to mind is to use heuristics to select the “best possible” move. By analogy with chess, we can evaluate each of the game positions obtained with our move, putting some assessment of this position.
Heuristic position evaluation
For example, in chess, it is quite simple to make an assessment (without getting into the wilds of debuts): at least, you can calculate the total “cost” of the pieces, taking the knight / bishop cost for 3 pawns, the value of the rook is 5 pawns, the queen is 9, the king is int .MaxValue pawns. Estimation is easy to improve, for example, by adding to it (with a correction factor — a multiplier / exponent or a function):
- the number of possible moves from the current position,
- the ratio of threats to enemy figures / threats from the enemy.
A special assessment is given to the position of the mat: int.MaxValue , if the mat has set the computer, int.MinValue if the mat has been set by the person.
If you order the chess processor to choose the next move, guided only by such an assessment, the processor will probably choose not the worst moves. In particular:
- do not miss the opportunity to take a bigger figure or checkmate,
- most likely not pounding the figures in the corners,
- it will not expose the figure once again (if we take into account the number of threats in the assessment).
Of course, such moves of the computer will not leave him a chance of success with the opponent making his moves more or less meaningful. The computer will ignore any of the forks. In addition, it does not hesitate to even probably exchange a queen for a pawn.
Nevertheless, the algorithm of the heuristic evaluation of the current playing position in chess (without claiming the laurels of the champion program) is quite transparent. What can not be said about the game Hare and Hedgehog.
In general, in the game Hare and Hedgehog, a rather vague maxim works: “ it’s better to go far away with more carrots and less lettuce ”. However, not everything is so straightforward. For example, if a player has 1 salad card in his hand in the middle of a game, this option can be quite good. But the player standing at the finish with a salad card, obviously, will be in a losing situation. In addition to the evaluation algorithm, I would also like to be able to “peep” a step further, just as in a heuristic evaluation of a chess position, you can count threats to the figures. For example, it is worth considering the bonus of carrots received by a player leaving a salad / cell position (1 ... 4), taking into account the number of players ahead.
I brought the final assessment as a function:
E = Ks * S + Kc * C + Kp * P,
where S, C, P are scores calculated by lettuce cards (S) and carrots © on the player’s hands, P is the score given to the player for the distance traveled.
Ks, Kc, Kp - the corresponding correction factors (they will be discussed later).
The easiest way I determined the grade for the distance traveled :
P = i * 3, where i is the index of the cell where the player is located.
Grade C (carrots) is made more difficult.
To get a specific C value, I choose one of 3 functions. from one argument (the number of carrots on hand). The index of the function C ([0, 1, 2]) is determined by the relative position of the player on the playing field:
- [0], if the player has passed less than half of the playing field,
- [2], if the player has enough (m. B., Even with an excess) carrots to finish,
- [1] in other cases.
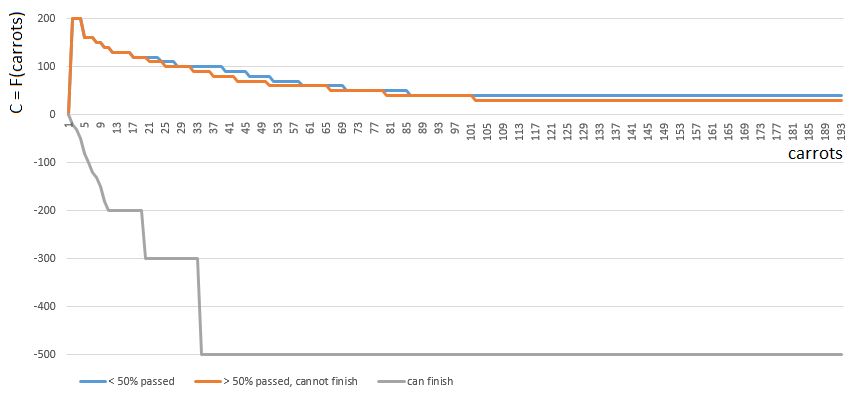
Functions 0 and 1 are similar: the “value” of each carrot in the hands of the player gradually decreases with increasing number of carrots in the hands. The game rarely encourages "Plyushkin." In case 1 (half of the field is passed), the value of the carrot decreases a little faster.
Function 2 (the player can finish), on the contrary, imposes a large penalty (negative coefficient value) on each carrot on the player's hands - the more carrots, the greater the penalty factor. Since with an excess of carrot finish is prohibited by the rules of the game.
Before calculating the number of carrots in the hands of the player is specified taking into account the carrots for the course from the lettuce cage / cell number 1 ... 4.
“ Salad ” score S is displayed in a similar way. Depending on the amount of salad on the player’s hands (0 ... 3), the function is selected. or . Function argument . - again, the “relative” path traveled by the player. Namely, the number of cells left in front (relative to the cell occupied by the player) with salad:
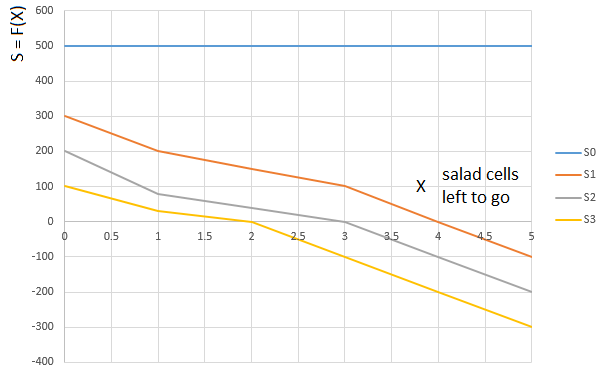
Curve - the evaluation function (S) of the number of lettuce cells in front of the player (0 ... 5), for a player with 0th lettuce cards on his hands,
curve - the same function for a player with one salad card on hand, etc.
The final score (E = Ks * S + Kc * C + Kp * P), therefore, takes into account:
- the additional amount of carrots that a player will receive immediately before his own turn,
- the path traveled by the player
- the number of carrots and lettuce on the hands, non-linearly affecting the assessment.
And this is how a computer plays, choosing the next move according to the maximum heuristic evaluation:
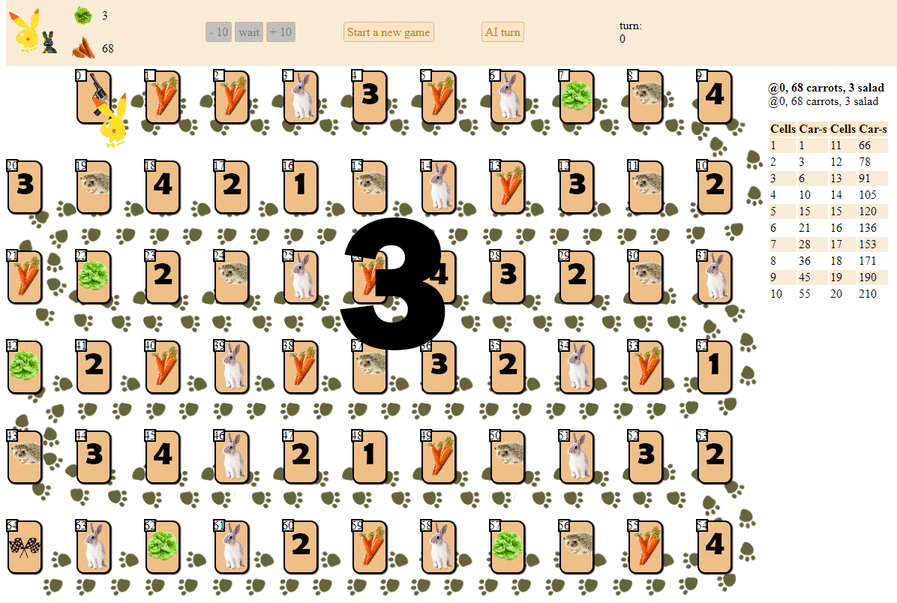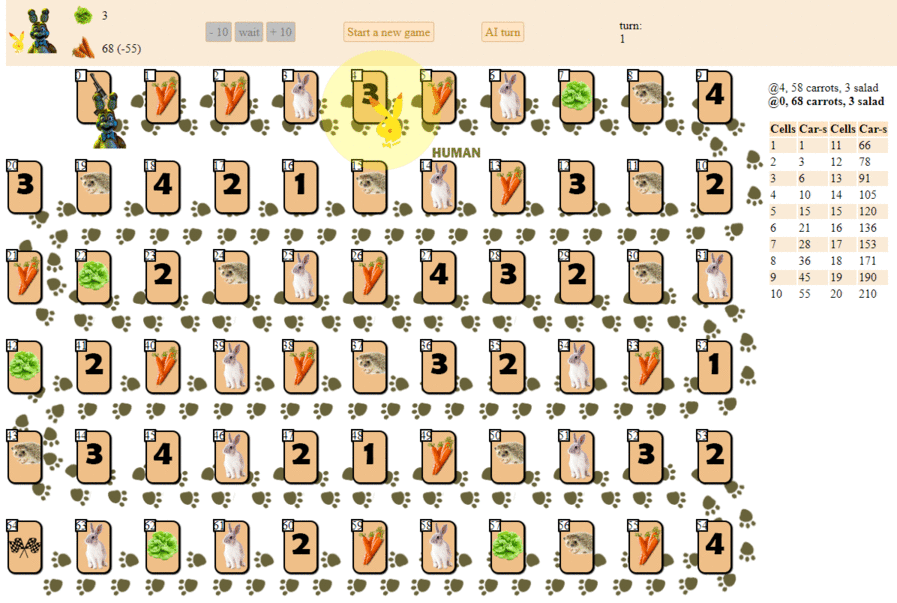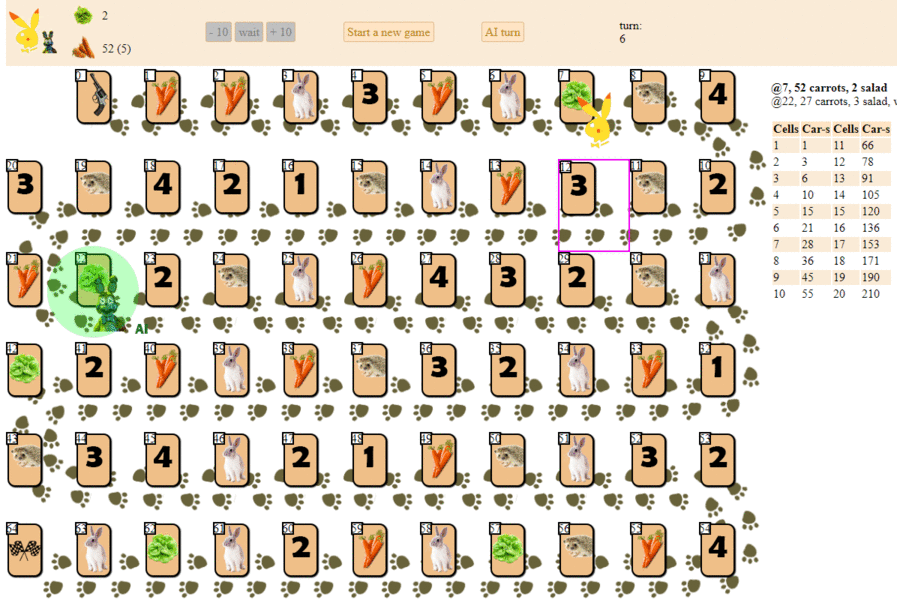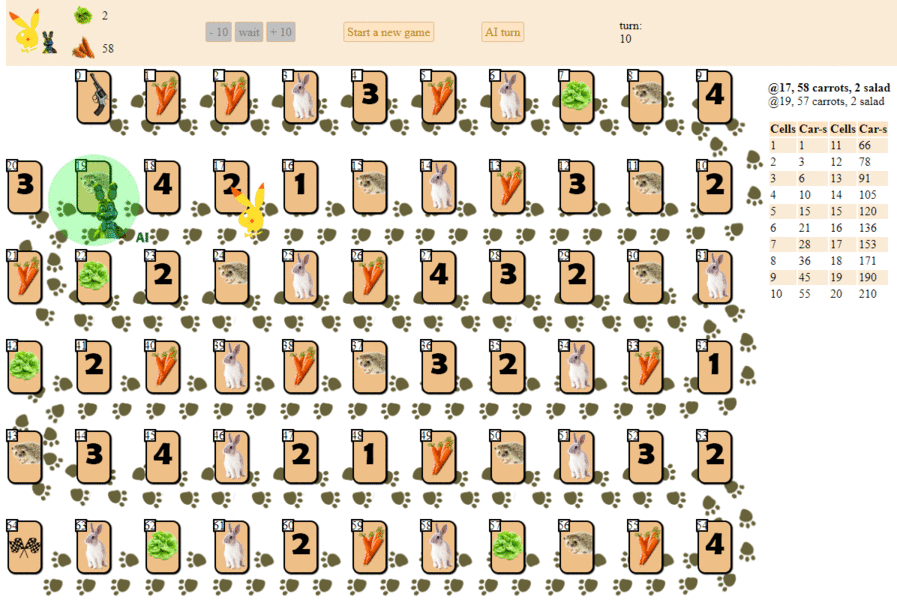
In principle, the debut is not so bad. However, one should not expect a good game from such an AI: by the middle of the game, the green “robot” begins to make repeated moves, and by the end it performs several iterations of moves forward - backward to the hedgehog, until finally it finishes. Finishes, partly due to chance, behind the player - a man for a dozen moves.
Implementation notes
Estimate is EstimationCalculator. Position evaluation functions for carrot - lettuce cards are loaded into arrays in the static constructor of the calculator class. At the input, the position estimation method receives the position object itself and the player's index, from the “point of view” of which the position is evaluated by the algorithm. That is, the same game position can receive several different ratings, depending on which player is considered to be virtual points.
Decision tree and Minimax algorithm
We use the decision-making algorithm in the antagonistic game “Minimax”. Very well, in my opinion, the algorithm is described in this post (translation) .
Teach the program to “look in” a few moves ahead. Suppose that from the current position (and the algorithm does not care about the prehistory - as we remember, the program functions as a Moore machine gun ), numbered 1, the program can make two moves. We will get two possible positions, 2 and 3. Next comes the turn of the player - the person (in the general case - the enemy). From the 2nd position, the opponent has 3 moves, from the third - only two moves. Next, the turn to make a move again falls to the program, which, in total, can make 10 moves out of 5 possible positions:
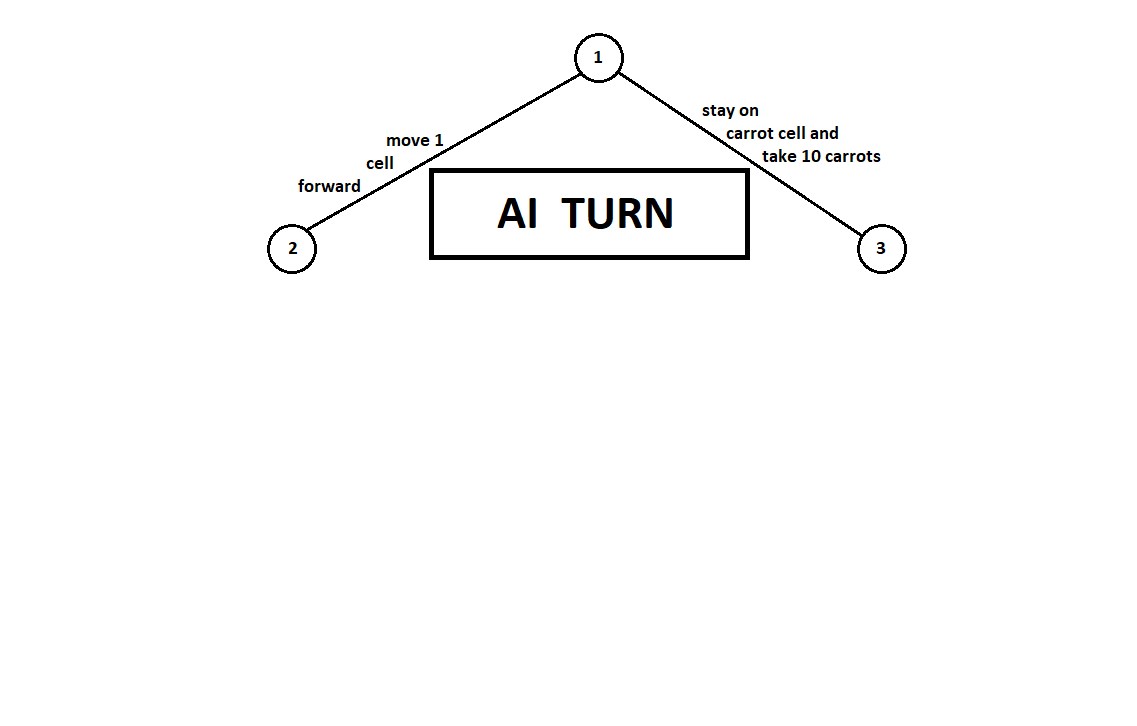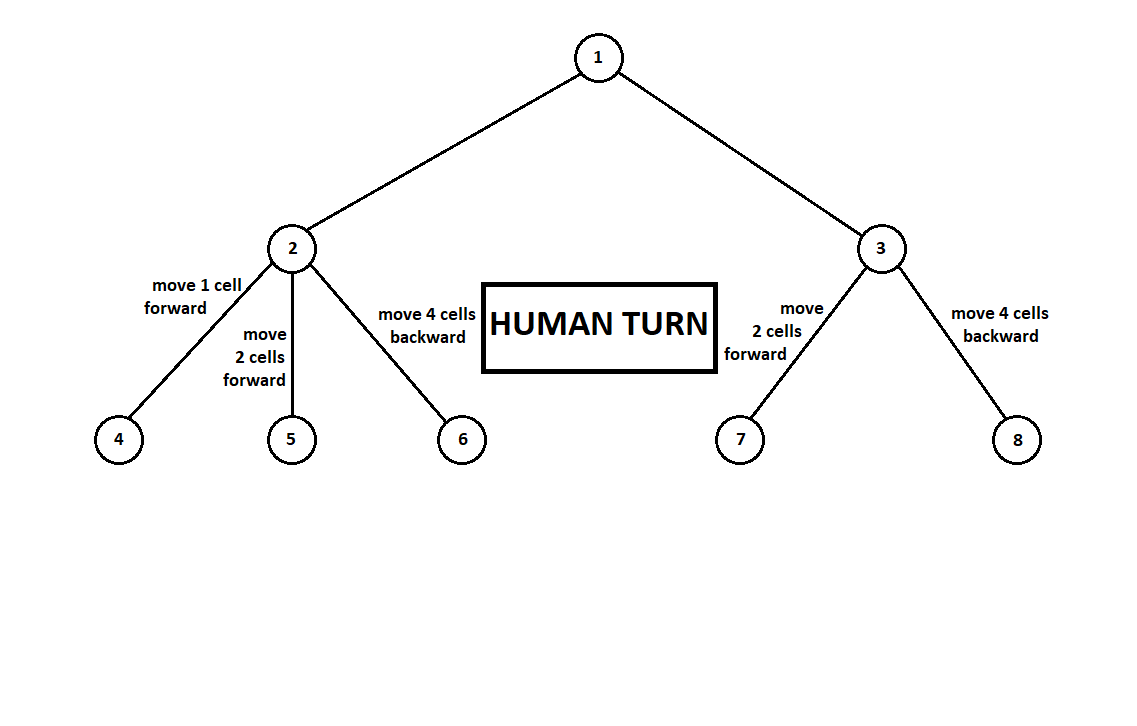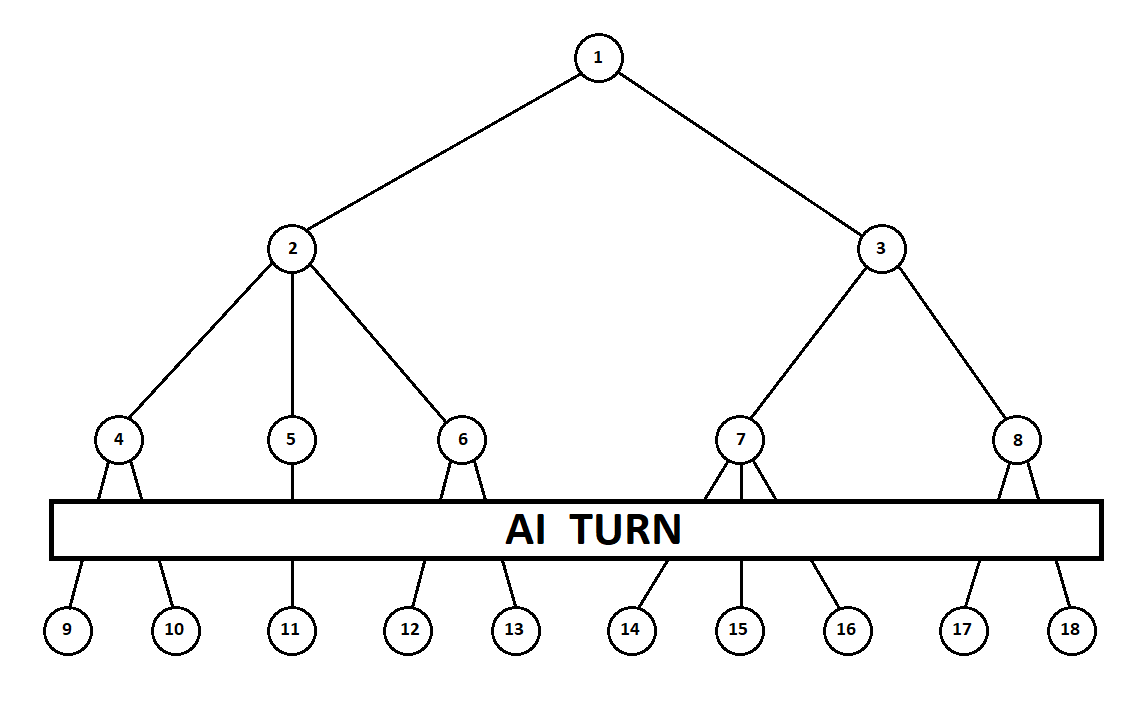
Suppose that after the second move of the computer the game ends and each of the positions obtained is evaluated from the point of view of the first and second players. And the evaluation algorithm we have already implemented. Let us evaluate each of the final positions (leaves of a tree 9 ... 18) in the form of a vector ,
Where - the score calculated for the first player, - second player's score:
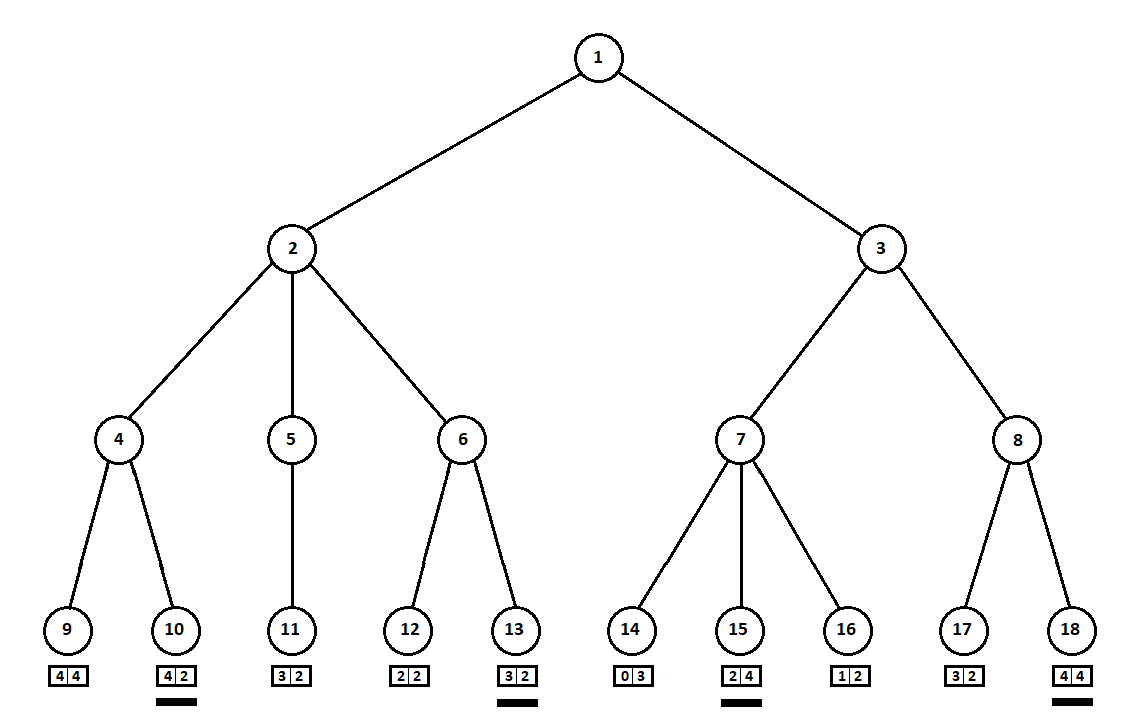
Since the last move is made by a computer, he will obviously choose in each of the subtree variants ([9, 10], [11], [12, 13], [14, 15, 16], [17, 18]) that which gives him a better grade. The question immediately arises: on what basis to choose the “best” position?
For example, there are two moves, after which we have positions with estimates [5; 5] and [2; one]. Evaluates the first player. Two alternatives are obvious:
- selection of the position with the maximum absolute value of the i-th score for the i-th player. In other words, the noble racer Leslie, eager to win, without looking at the competition. In this case, the position with the estimate will be selected [5; five].
- choosing a position with a maximum rating relative to competitor ratings is a cunning professor Faith, who does not miss the opportunity to inflict a dirty trick on the enemy. For example, deliberately falling behind the player who plans to start from the second position. The position with the estimate will be selected [2; one].
In my software implementation, I made an evaluation selection algorithm (a function that maps the evaluation vector to a scalar value for the i-th player) as a configurable parameter. Further tests showed, to some surprise to me, the superiority of the first strategy — the choice of position by the maximum absolute value. .
Features of software implementation
If the first choice of selecting the best estimate is specified in the AI settings (of the TurnMaker class), the code of the corresponding method takes the form:
The second method - maximum relative to the positions of competitors - is implemented a little more complicated:
int ContractEstimateByAbsMax(int[] estimationVector, int playerIndex) { return estimationVector[playerIndex]; } The second method - maximum relative to the positions of competitors - is implemented a little more complicated:
int ContractEstimateByRelativeNumber(int[]eVector, int player) { int? min = null; var pVal = eVector[player]; for (var i = 0; i < eVector.Length; i++) { if (i == player) continue; var val = pVal - eVector[i]; if (!min.HasValue || min.Value > val) min = val; } return min.Value; } The selected estimates (underlined in the figure) are moved up one level. Now, the opponent will have to choose a position, knowing which subsequent position the algorithm will choose:
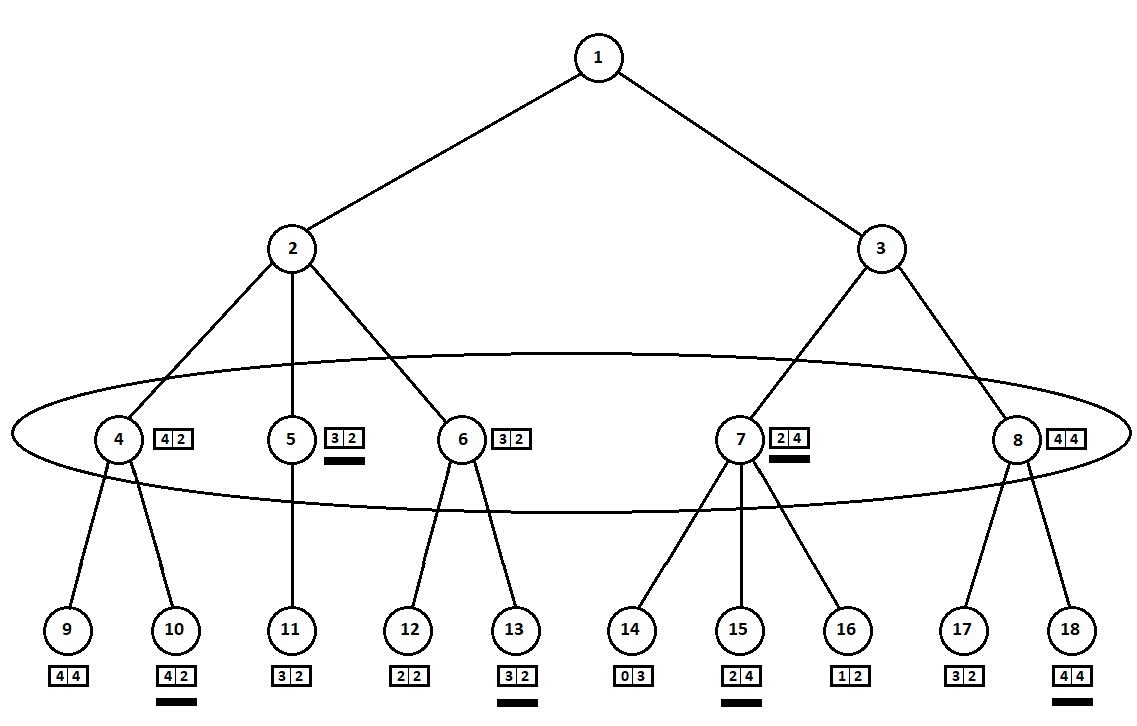
The enemy will obviously choose the position with the best estimate for himself (the one where the second coordinate of the vector takes the greatest value). These ratings are again underlined in the graph.
Finally, we return to the very first move. Selects a computer, and he prefers the move with the largest first coordinate of the vector:
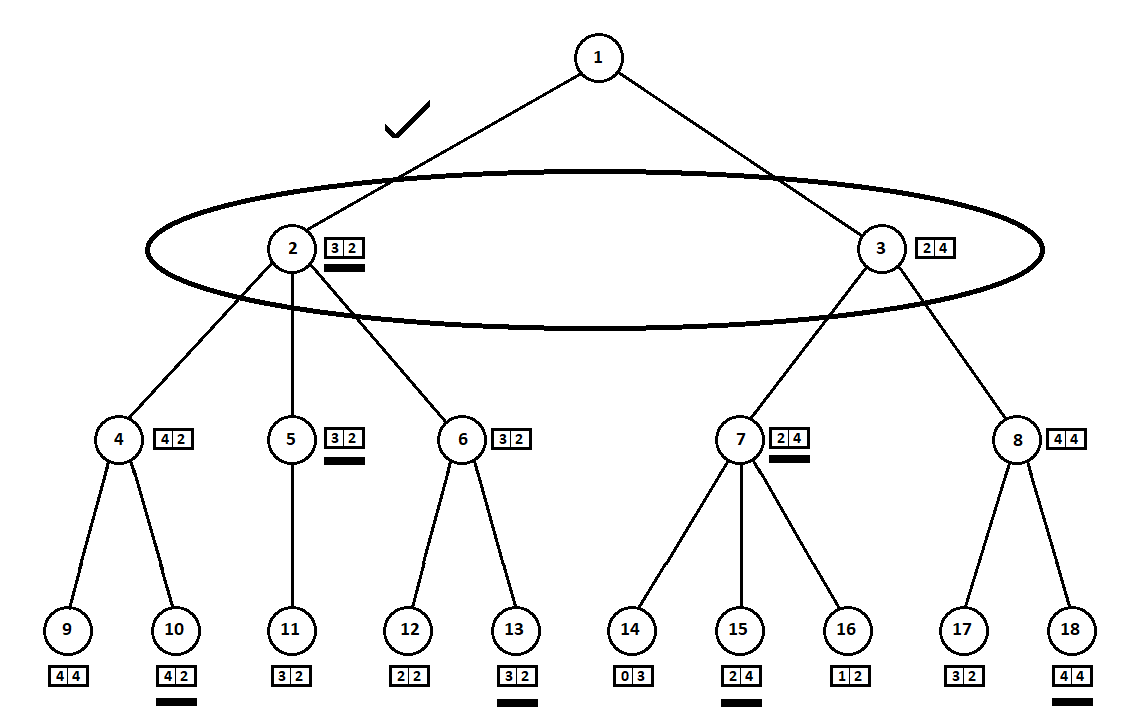
Thus, the problem is solved - a quasi-optimal move is found. Suppose a heuristic estimate in the leaf positions of a tree is 100% indicating the future winner. Then our algorithm will definitely choose the best possible move.
However, the heuristic estimate is 100% accurate only when the final position of the game is evaluated - one (or several) players finished, the winner was determined. Therefore, having the opportunity to look at N moves ahead - as much as it takes to win rivals equal in strength, you can choose the optimal move.
But a typical game for 2 players lasts on average about 30 - 40 moves (for three players - about 60 moves, etc.). From each position, the player can make, as a rule, about 8 moves. Consequently, a full tree of possible positions for 30 moves will consist of approximately
= 1237940039285380274899124224 vertices!
In practice, building and “parsing” a tree from ~ 100,000 positions on my PC takes about 300 milliseconds. That gives us a limit on the depth of the tree in 7 - 8 levels (moves), if we want to wait for the computer to respond by no more than a second.
Features of software implementation
To build a tree of positions and find the best move, obviously, you need a recursive method. At the input of the method is the current position (in which, as we remember, the player who performs the move is already indicated) and the current level of the tree (the move number). As soon as we descend to the maximum level allowed by the algorithm settings, the function returns the heuristic position estimation vector from the “point of view” of each player.
An important addition : the descent below the tree must be stopped also in the case when the current player has finished. Otherwise (if the algorithm for selecting the best position relative to the positions of other players is chosen), the program can “trample” at the finish for a rather long time, “mocking” the opponent. In addition, we reduce the size of the tree in the endgame a little.
If we are not yet at the limit of the recursion level, then we select the possible moves, create a new position for each move and pass it to the recursive call of the current method.
An important addition : the descent below the tree must be stopped also in the case when the current player has finished. Otherwise (if the algorithm for selecting the best position relative to the positions of other players is chosen), the program can “trample” at the finish for a rather long time, “mocking” the opponent. In addition, we reduce the size of the tree in the endgame a little.
If we are not yet at the limit of the recursion level, then we select the possible moves, create a new position for each move and pass it to the recursive call of the current method.
Why “Minimax”?
In the original interpretation of the players are always two. The program calculates the score only from the position of the first player. Accordingly, when choosing the “best” position, a player with index 0 searches for a position with a maximum rating, a player with index 1 - with a minimum.
In our case, the score should be a vector, so that each of the N players can evaluate it from their “point of view” as the score goes up the tree.
In our case, the score should be a vector, so that each of the N players can evaluate it from their “point of view” as the score goes up the tree.
Tuning AI
My practice of playing against the computer has shown that the algorithm is not so bad, but still so far inferior to man. I decided to improve AI in two ways:
- optimize the construction / passage of the decision tree,
- improve heuristics.
Optimization algorithm Minimax
In the example above, we could refuse to consider position 8 and “save” 2 - 3 tree tops:
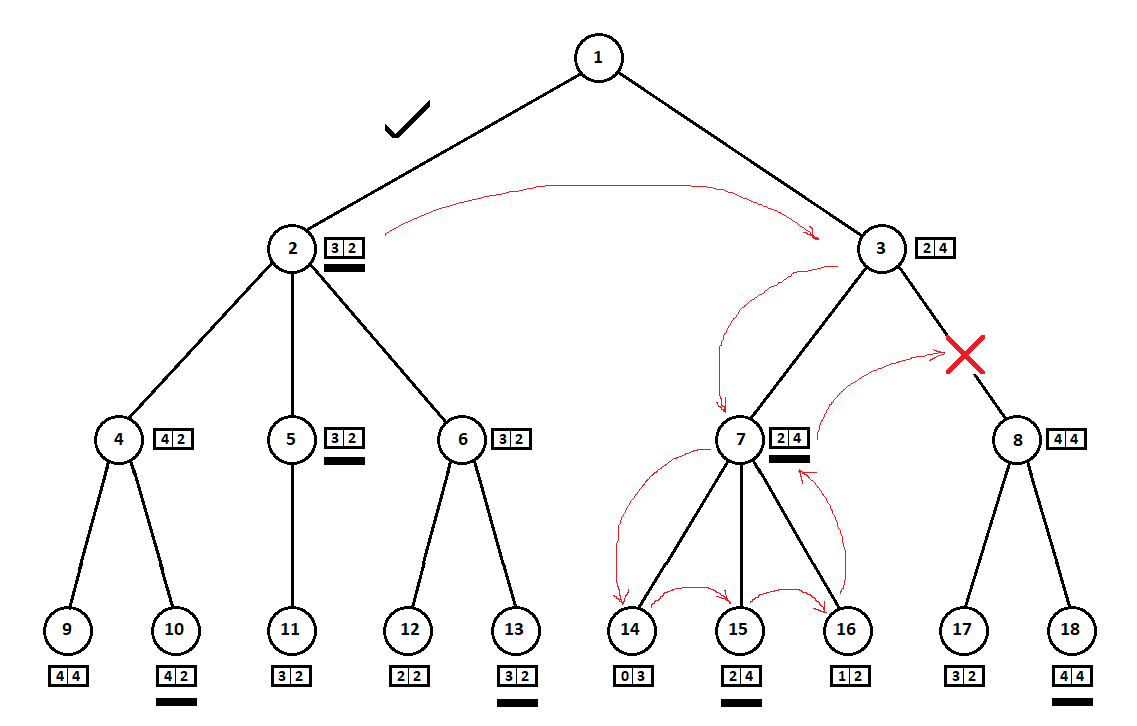
We walk the tree from top to bottom, from left to right. Bypassing the subtree starting at position 2, we derived the best mark for move 1 -> 2: [3, 2]. Passing the subtree rooted at position 7, we determined the current (best for move 3 -> 7) grade: [2, 4]. From the point of view of the computer (first player), the rating [2, 4] is worse than the rating [3, 2]. And since the opponent of the computer chooses the move from position 3, whatever the estimate for position 8, the final assessment for position 3 will be a priori worse than the estimate obtained for the third position. Accordingly, the subtree rooted at position 8 can be not built or evaluated.
The optimized version of the Minimax algorithm, which allows you to cut off extra subtrees, is called the alpha-beta cut-off algorithm . To implement this algorithm, minor modifications to the source code will be required.
Features of software implementation
In addition, two integer parameters are transferred to the CalcEstimate method of the TurnMaker class - alpha, which is initially equal to int.MinValue and beta, equal to int.MaxValue. Further, after receiving an estimate of the current considered move, the following pseudo-code is executed:
e = _[0] // ( ) (e > alpha) alpha = e (e < beta) beta = e (beta <= alpha) Important feature of the software implementation
The alpha-beta pruning method leads to the same solution as the “pure” Minimax algorithm. To check whether the decision logic (or rather, the results - the moves) changed, I wrote a unit test in which the robot made 8 moves for each of the 2 opponents (16 moves in total) and saved the resulting series of moves - cut off option.
Then, in the same test, the procedure was repeated with the cut-off option enabled. Then the sequence of moves were compared. The discrepancy in the moves indicates an error in the implementation of the alpha-beta cut-off algorithm (test failed).
Then, in the same test, the procedure was repeated with the cut-off option enabled. Then the sequence of moves were compared. The discrepancy in the moves indicates an error in the implementation of the alpha-beta cut-off algorithm (test failed).
Small optimization of the alpha-beta clipping algorithm
With the cut-off option enabled in the AI settings, the number of vertices in the position tree decreased on average by 3 times. This result can be slightly improved.
In the example above:

so successfully “coincided” that, before the subtree with the top in position 3, we looked at the subtree with the top in position 2. If the order were different, we could start with the “worst” subtree and not conclude that there is no point in considering the next position .
As a rule, clipping on a tree is more “economical”, the vertices of which are on the same level (i.e., all possible moves from the i-position) are already sorted by the current position estimate (without looking inwards). In other words, we assume that from the best (from the point of view of heuristics) progress there is a greater chance of getting a better final grade. Thus, we are, with some probability, sorting the tree so that the “best” subtree will be considered before the “worst”, which will allow cutting off more options.
Evaluating the current position is a costly procedure. If before it was enough for us to evaluate only the terminal positions (leaves), now the assessment is made for all tree tops. However, as the tests showed, the total number of assessments made was still somewhat less than in the variant without the initial sorting of possible moves.
Features of software implementation
The alpha-beta clipping algorithm returns the same course as the original Minimax algorithm. This is checked by a unit test written by us that compares two sequences of moves (for an algorithm with and without clipping). Alpha-beta pruning with sorting , in general, may indicate a different move as a quasi-optimal.
To test the correct operation of the modified algorithm, we need a new test. Despite the modification, the sorting algorithm should produce exactly the same final evaluation vector ([3, 2] in the example in the figure) as the non-sorting algorithm as the original Minimax algorithm.
In the test, I created a series of test positions and selected one for each of the “best” moves, including disabling the sorting option. After that, he compared the vector estimates obtained in two ways.
To test the correct operation of the modified algorithm, we need a new test. Despite the modification, the sorting algorithm should produce exactly the same final evaluation vector ([3, 2] in the example in the figure) as the non-sorting algorithm as the original Minimax algorithm.
In the test, I created a series of test positions and selected one for each of the “best” moves, including disabling the sorting option. After that, he compared the vector estimates obtained in two ways.
Additionally, since the positions for each of the possible moves in the current vertex of the tree are sorted by heuristic evaluation, the idea suggests that we should immediately discard some of the worst options. For example, a chess player may consider a move in which he substitutes his own rook under the blow of a pawn. However, “unwinding” the situation deeper by 3, 4 ... moves forward, he immediately marks out the options when, for example, the enemy submits his queen for an elephant.
In the AI settings, I set the “cut-off worst case” vector. For example, a vector of the form [0, 0, 8, 8, 4] means that:
- looking at one [0] and two [0] steps forward, the program will consider all possible moves, because 0 ,
- [8] [8] , 8 “” , , ,
- [4], 4 “” .
- 300 , “” 8 .
“” , AI . “ ”.
. ( 8 — 10 15), . “” ( !):
. :
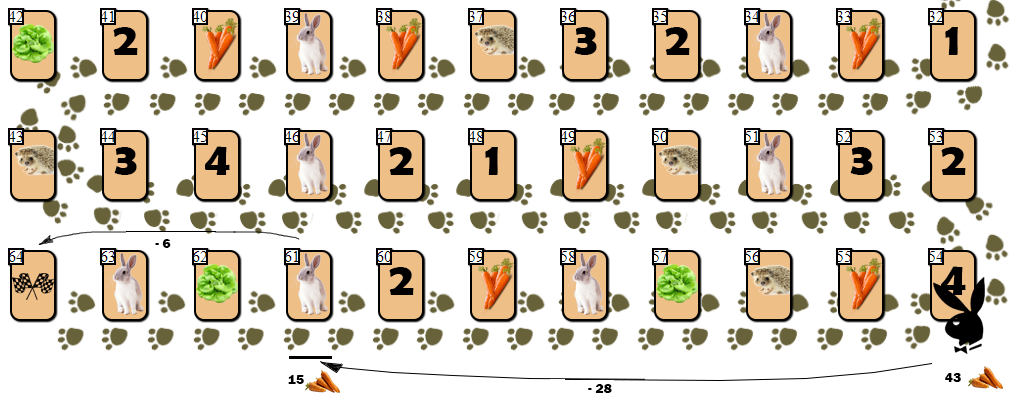
54 (43), — 10 55 . AI, , (61), 28 . , 6 9 ( 10 ).
, ( ), , 4 — 6 . , , , AI ?
, , . AI . , , . “ ” :
65 — “” , , . , , , () .
- 7,
- , , . , , , .
. :

54 (43), — 10 55 . AI, , (61), 28 . , 6 9 ( 10 ).
, ( ), , 4 — 6 . , , , AI ?
, , . AI . , , . “ ” :
65 — “” , , . , , , () .
,
E = Ks * S + Kc * C + Kp * P,
, .
, , , , , .. “ ”. , , Ks, Kc Kp, .
“” ? — , . :
“”, CSV
45;26;2;f;29;19;0;f;2 ... :
- 45 , 26 2 , (f = false). .
- 29 19 , .
- , , “” , , .
20 , “” web-, . , , , “”. , .
20 (, ), . , 0.5 2 0.1 — = 4096 . , ( 1), “”. . .
, “” (16 20). 250 4096 , “”, , “ ”, AI.
Results
, , , , . . , AI . , .
, ( ), , , . , i- , , ( ).
3- . , “” AI 3- , . , — , , “”.
AI — “”, .., “”. .
→
Source: https://habr.com/ru/post/432382/
All Articles