Sound modulation
A bit of theory that I know about sound is sound:
wave, oscillations, damped oscillations, a wave can be described from the point of view of physics, a wave can be described from the point of view of mathematics.
Download and test the program
As we model on a computer, our wave is described using a sequence (Fourier series) of bytes (numbers from -128 to 127 and zero), that is, an array of bytes.
')
The oscillation equation is best described by the SIN function.
Agree, it would be too easy if we just ran the SIN function through the array.
Therefore, guided by the articles about the description of the device synthesizer Yamaha, I wrote the following algorithm:
1. Using the SIN function, a main or modeling wave is created, here is a formula that can be useful to another developer:
Where:
amplitude1 - amplitude
frequency1 - oscillation frequency
faza - the initial phase of oscillation
2. With the help of the second function SIN, the main wave is created, with the amplitude in which the values of the first wave are:
Program screenshot
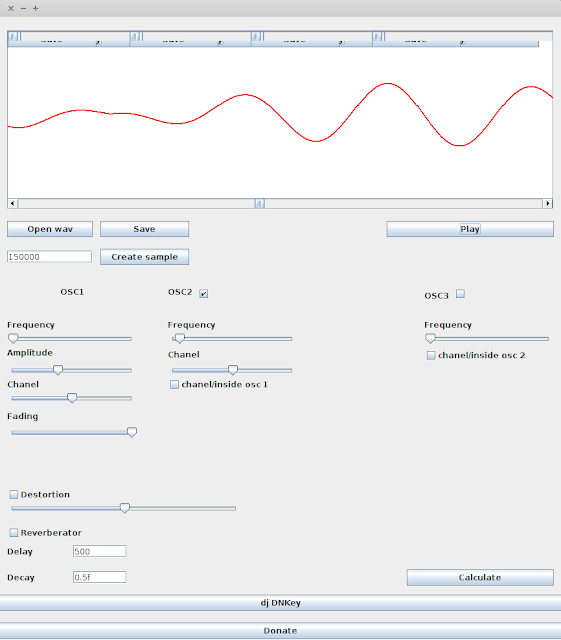
I downloaded the test sounds into the lmms program.

Listen to mp3
Another algorithm will be implemented, which will work through the channels, if I can write about it in the second article.
Update:
According to the comments of commentators, the algorithms can now be multiplied by themselves and among themselves.
Update 2: The program is updated, now the wave can be mixed into the sound.
wave, oscillations, damped oscillations, a wave can be described from the point of view of physics, a wave can be described from the point of view of mathematics.
Download and test the program
As we model on a computer, our wave is described using a sequence (Fourier series) of bytes (numbers from -128 to 127 and zero), that is, an array of bytes.
')
The oscillation equation is best described by the SIN function.
Agree, it would be too easy if we just ran the SIN function through the array.
Therefore, guided by the articles about the description of the device synthesizer Yamaha, I wrote the following algorithm:
1. Using the SIN function, a main or modeling wave is created, here is a formula that can be useful to another developer:
for(int k = 0; k < SoundLabVisual.player.data.length;k++){ double sinusoid = amplitude1 * Math.sin(2 * (3.14/1 ) * k * frequency1 + faza); } Where:
amplitude1 - amplitude
frequency1 - oscillation frequency
faza - the initial phase of oscillation
2. With the help of the second function SIN, the main wave is created, with the amplitude in which the values of the first wave are:
//c double a1 = 0.1f; //c double c1 = 0.1f; //c double d1 = 0.1f; sinusoid = a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 )); Program screenshot

I downloaded the test sounds into the lmms program.

Listen to mp3
Another algorithm will be implemented, which will work through the channels, if I can write about it in the second article.
Update:
According to the comments of commentators, the algorithms can now be multiplied by themselves and among themselves.
if(jCheckBox8.isSelected()){ sinusoid = (a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 ))) * (a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 ))); }else{ sinusoid = a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 )); } Update 2: The program is updated, now the wave can be mixed into the sound.
Source: https://habr.com/ru/post/431488/
All Articles