Looking for promising shadows for roguelike

Dear Habrovchane, I present to your attention the continuation of research on the topic of finding suitable shadows for a 2D bagel.
This post is a sequel to the publication , a kind of work on the mistakes and further development of the idea.
In their comments, respected critics, quite rightly pointed out that in confined spaces the shadows turned out to be angular and somewhat unnatural. Several solutions were suggested, I liked the suggestion to use ray casting to calculate the shadow.
')

I’m clarifying that I’m not working with a video card (I’m not working yet), all the results are modeled on the CPU.
In this work on reykasting, we understand the method of constructing an image by throwing rays from an observer into space before crossing with an obstacle (screen boundaries) and highlighting the place of their collision.
Here we will use a simplified version of reykasting, based on the intersection of the beam grid. This method was widely used in the pseudo-three-dimensional games of the past (for example, Wolfenstein_3D , deference to those who are in the subject), we adapt it for two-dimensional space.
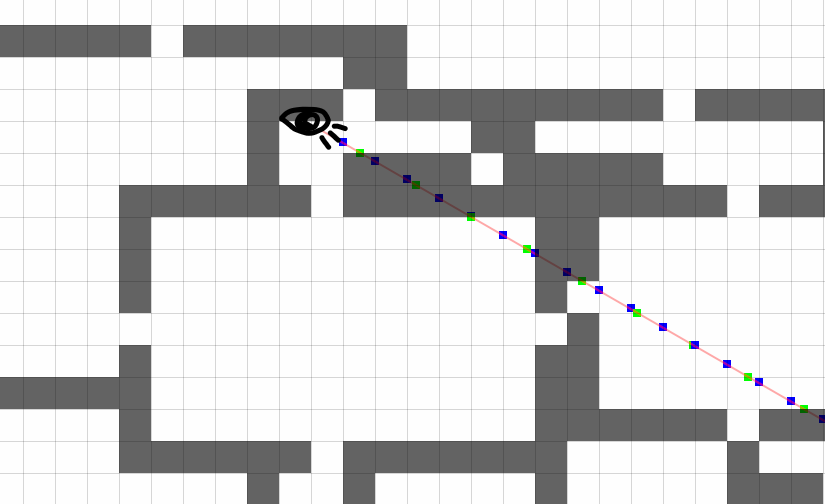
The algorithm is simple enough for both understanding and implementation. I will give its own implementation:
Pascal
// i,j - , - // X,Y - // r - // if cos(a)<0 then begin di :=-1; ddi:= 0; end else begin di := 1; ddi:= 1; end; if sin(a)<0 then begin dj :=-1; ddj:= 0; end else begin dj := 1; ddj:= 1; end; // Y x1 := (i+ddi) * tile_size; y1 := y+ (x1-x) * tan(a); Dx := len(x,y,x1,y1); y1 := (j+ddj) * tile_size; x1 := x+ (y1-y) * cotan(a); Dy := len(x,y,x1,y1); sum_lenX := 0; sum_lenY := 0; // X Y a rX := abs(tile_size / cos(a)); rY := abs(tile_size / sin(a)); // repeat if sum_lenX+DX < sum_lenY+DY then begin x1 := (i+ddi) * tile_size; y1 := y+ (x1-x) * tan(a); i := i+di; // key := is_wall(i,j); sum_lenX := sum_lenX + DX; if DX<>rX then DX:=rX; // if r<sum_lenX then Break; end else begin y1 := (j+ddj) * tile_size; x1 := x+ (y1-y) * cotan(a); j := j+dj; // key := is_wall(i,j); sum_lenY := sum_lenY + DY; if DY<>rY then DY:=rY; // if r<sum_lenY then Break; end; until ( ); // x1,y1 Since the beam crosses the cells along each axis at the same distance, you can save on calculations and only check if there are no walls within the boundaries of the tile. We need an intersection with an obstacle and memorize its coordinates.
In my implementation, I carried out all trigonometry and divisions into a separate table for each angle, which greatly accelerated the algorithm.
Starting the rays in all directions with the right step, we get something like this:
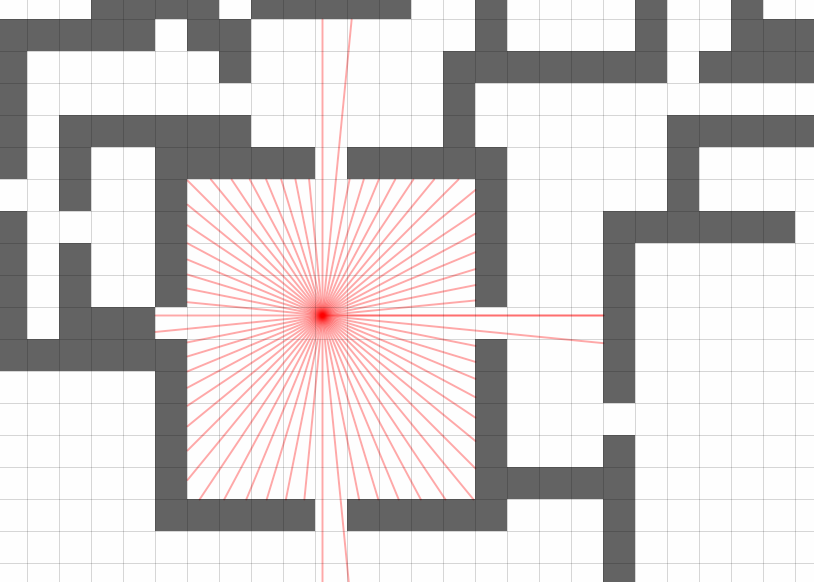
Increasing the number of rays to several thousand and we obtain the desired polyhedron of the scope. It is possible, of course, to throw rays for each pixel of the image, as on 3D accelerators, but you cannot do without a video card.
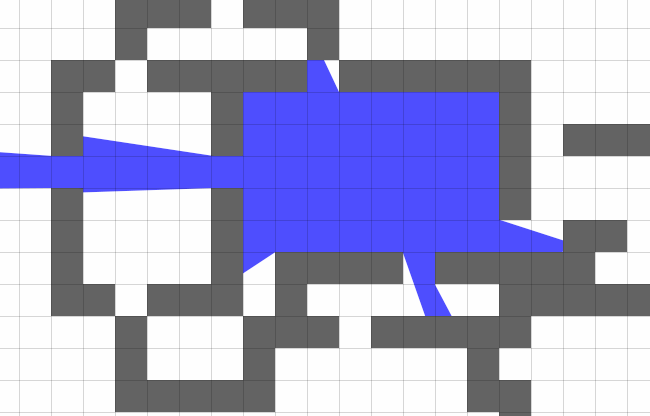
Further work with layers begins.
Area of visibility. Here and below, the rays slightly penetrate the objects. This game convention creates a unique surroundings, typical of the 2D Game.

Lightmap generation We generate static light sources in advance and cache them to improve speed, we impose dynamic ones during the output to the screen.

Keeping everything together. All that is missing is creepy monsters and treasure ... many treasures.

The walls with variable curvature of light penetration did not come to me, but maybe this is an amateur.

In the process of creating a prototype, I tried many variations of the model, some of them are better suited for horror :
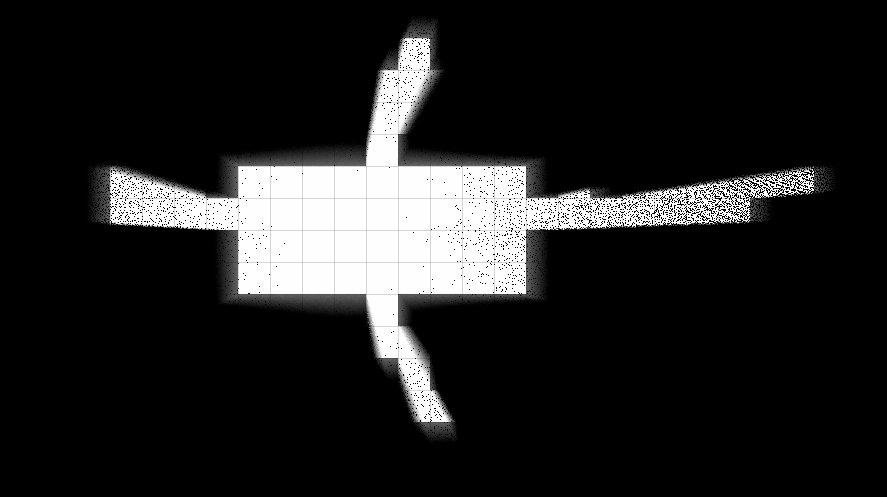
I especially liked the effect of multiple reflections of the rays from the walls, but even its naive implementation slowed down so much that I left it for the future when I became friends with the video card.
Thanks for attention.
Link play (exe for windows)
Source: https://habr.com/ru/post/431304/
All Articles