From the Geiger counter, matches and arduins. Part One - Theory
It has long been no problem to buy a device under the conditional name “household dosimeter” (there was money - in this sense, Fukushima radio phobia and radio physics (TM) podgadila), but I think that this device would be interesting to do with your own hands.

The heart of our device will be a Geiger counter. We know, of course, that this detector has a lot of flaws and in general “the device must be scintillation”, but the scintillation radiometer is much more complicated and I have the next post for it. Moreover, the Geiger-Muller counter has a number of undeniable advantages.
So, let's begin.
So, the Geiger-Muller counter. (Fig. 1) The simplest device consisting of two electrodes placed in a gaseous medium at low pressure is a cathode having a large area and an anode in the form of more or less thin wire creating a local field of great intensity. in which the process of multiplication of ions develops, due to which a single ion pair can cause a powerful avalanche of ionization and the ignition of an independent discharge.
')

Fig. 1. Geiger-Muller counter. 1 — anode, 2 — cathode, 3 — balloon, 4 — cathode lead, 5, 6 — springs tightening the cathode filament.
In fact, the counter works like a cold cathode thyratron, only the discharge in it is ignited by ionization, caused not by a pulse from the grid, but by a charged particle flying through the gas. After the discharge has caught fire, it must be extinguished either by removing the voltage from the anode, or ... Or it will go off itself. But for this purpose, it is necessary to introduce something into the gas medium of the meter, which under the action of the discharge will turn into a form that will make the gas opaque to ultraviolet radiation and because of this one of the factors for maintaining an independent discharge - photoelectric emission - will disappear. There are two such additives: alcohol and halogens (chlorine, bromine and iodine). The first in the discharge decomposes, turning, roughly speaking, into soot, and then does not turn back into alcohol, and after a few tens of thousands of pulses will end and the meter ends. And halogens become molecular atomic from, and the process is reversible. They also end - due to the fact that atomic halogens easily react with everything, including the counter walls, but more often they have time to recombine with each other, therefore halogen counters are much more durable, withstanding billions of pulses. We are primarily interested in halogen meters, because:
a) they are more durable
b) they operate at 400-500 V, and not at one and a half thousand, like alcohol,
c) they are simply the most common.
In Table 1, I listed several common Geiger counters and their main parameters.
Table 1.
The main parameters of some Geiger-Muller counters.
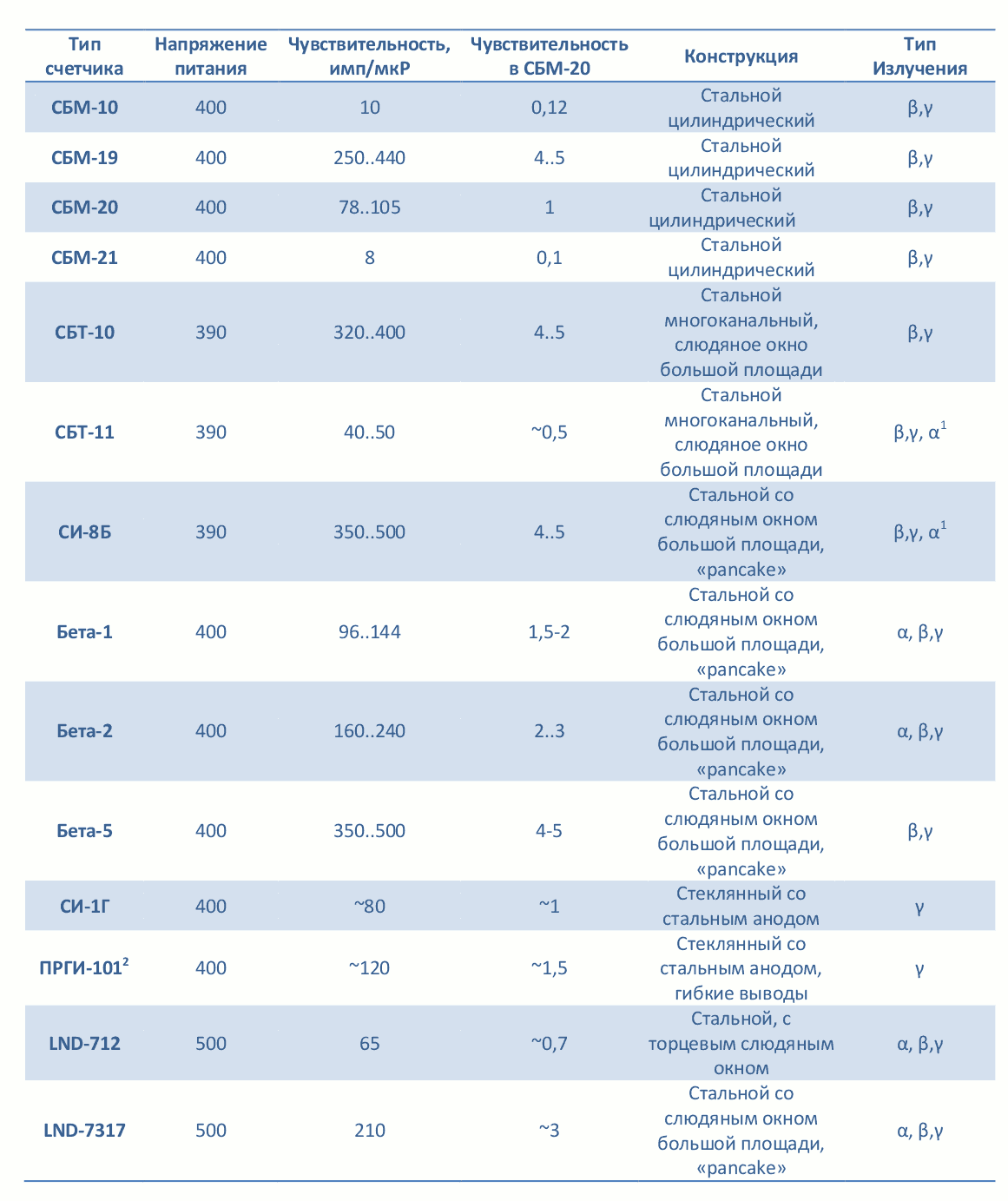
Notes: 1 - sensitivity to alpha radiation is not regulated; 2 - small-scale counter, the data on it is scarce.
When choosing a Geiger counter for our dosimeter, you must first look at its sensitivity. After all, it is unlikely that you want a device that will show something only where Kuzkina Mother exploded a couple of hours ago. But there are plenty of such meters, and for their almost complete uselessness for the average man, they are very cheap. These are all sorts of SI-3BG, SI-13G and other “doomsday counters” standing in army dosimeters for work at the upper limit of measurements. The more sensitive the counter, the more pulses per second it will give at the same level of radiation. The classic SBM-20 counter (also known as the earlier issues was called STS-5), which was traditionally put into all reorganization-post-Chernobyl “ratchets”, with a natural background of 12 μR / h gives about 18 pulses per minute. From this figure it is convenient to dance, considering the sensitivity of the counter in the "SBM-20".
What gives us the sensitivity of the counter? Accuracy and speed of reaction. The fact is that the particles of radioactive radiation arrive to us not according to the schedule, but as it should be, and some of them will miss the counter, but from some of them will work (from photons of gamma radiation - approximately from one of several hundreds). So the pulses from the Geiger counter (and from any counting radiation detector) come at absolutely random times with unpredictable intervals between them. And counting the number of pulses in one minute, another, the third - we get different values. And the standard deviation of these values, that is, the error in determining the counting rate, will be proportional to the square root of the number of recorded pulses. The greater the number of pulses, the smaller will be the relative (as a percentage of the measured value) error in their counting:
When we have a detector — the mentioned “reference” SBM-20, and the counting time — 40 seconds (this was done in simple household dosimeters, directly showing the number of counted pulses as a dose rate level in μR / h), on a natural background the number of pulses is ~ 10 pieces. And this means that the standard deviation is about three. And the error at 95% confidence level is twice as large, that is, 6 pulses. Thus, we have a sad picture: the dosimeter readings of 10 μR / h mean that the dose rate is somewhere from 4 to 16 μR / h. And we will be able to talk about the detection of an anomaly only when the dosimeter shows a deviation of three sigmas, that is, more than 20 μR / h ...
To increase accuracy, you can increase the counting time. If we make it three minutes, that is, four times more, we will quadruple the number of pulses, which means we double the accuracy. But then we will lose the response of the device to short bursts of radiation, for example, at the “Your Excellency” that passed by you after scintigraphy or radioiodine therapy or vice versa, when you pass by the radio base past the SPD clock. And taking four times more sensitive detector (4 parallel-connected SBM-20, one SBM-19, SBT-10 or SI-8B) and leaving the same measurement time, we will increase the accuracy and maintain the speed of the reaction.
Alpha radiation is delayed by a piece of paper. Beta radiation can be shielded with a plexiglass sheet. And from hard gamma radiation you need to build a wall of lead bricks. This is probably all know. And all this has a direct bearing on Geiger counters: in order for him to sense the radiation, it is necessary that it at least penetrate inside. And it should not fly right through, like a neutrino through the Earth.
The SBM-20 type counter (and its older brother the SBM-19 and the younger ones of the SBM-10 and the SBM-21) have a metal casing, in which there are no special entrance windows. From this it follows that there is no question of any sensitivity to alpha radiation. Beta rays he feels quite well, but only if they are tough enough to get inside. This is somewhere from 300 keV. But he feels the gamma radiation, starting with a couple of dozen keV.
And the SBT-10 and SI-8B counters (as well as the new-fashioned and inaccessible because of the scrap prices Beta-1, 2 and 5) instead of a solid steel shell have an extensive window of thin mica. Beta particles with energies above 100-150 keV are able to penetrate through this window, which makes it possible to see carbon 14 pollution, which is completely invisible to steel counters. Also, a window of mica allows the counter to feel alpha particles. True, in relation to the latter, it is necessary to look at the thickness of the mica specific meters. So, SBT-10 with its thick mica practically does not see it, while Beta-1 and 2 have thinner mica, which makes the registration efficiency of alpha particles of plutonium-239 about 20%. SI-8B - somewhere in the middle between them.
And now with regard to the passage through. The fact is that the alpha and beta particles of the Geiger counter registers almost everything that could penetrate inside. But with gamma rays everything is sad. In order for a gamma quantum to trigger a pulse in a counter, it must knock an electron out of its wall. This electron must overcome the thickness of the metal from the point where the interaction occurred, to the inner surface, and therefore the “working volume” of the detector, where it interacts with the photons of gamma radiation, is the thinnest, several microns, layer of metal. From this it is clear that the efficiency of the counter for gamma radiation is very small — a hundred or more times less than for beta radiation.
For the Geiger counter operation requires high voltage power. Typical Soviet-Russian halogen devices require a voltage of about 400 V, many western meters are rated for 500 or 900 V. Some meters require voltages up to one and a half kilovolts - these are old meters with alcohol quenching of the type MS and BC, X-ray counters for X-ray analysis, neutron . They will not interest us much. Power is supplied to the meter through the ballast resistance of a few megaohms - it limits the current pulse and reduces the voltage at the counter after the pulse, facilitating damping. The magnitude of this resistance is given in the reference data for a specific device — its too small a magnitude shortens the life of the detector, and too much increases the dead time. It can usually be taken at about 5 megohms.
When the voltage increases from zero, the Geiger counter first works like an ordinary ionization chamber, and then as a proportional counter: each of the pairs of ions that were formed during the passage of a particle produces small ions, increasing the ion current hundreds and thousands of times. At the same time, very weak impulses measured by millivolts can already be detected on the load resistance in the counter circuit. As the voltage rises, avalanches become more and more, and at some point the strongest of them begin to support themselves, igniting an independent discharge. At this moment, instead of weak millivolt pulses from avalanches passing through the interelectrode space and disappearing at the electrodes, gigantic, with an amplitude of several tens of volts, appear! And their frequency grows rapidly with increasing voltage, until each avalanche starts to cause a flash of discharge. Obviously, with a further increase in voltage, the counting rate should stop growing. So it happens: a plateau is observed on the dependence of sensitivity on voltage.
Nevertheless, the increase in voltage does not leave the counting rate unchanged: a discharge may arise just as a result of spontaneous emission. And with increasing voltage, the probability of such a discharge only increases. Therefore, the plateau is oblique, and starting from a certain voltage, the counting rate begins to grow rapidly, and then the discharge becomes continuous. In this mode, of course, the meter not only fails to fulfill its function, but also quickly fails.
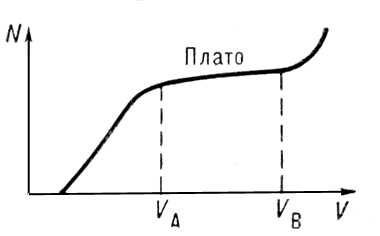
Fig. 2. The dependence of the counting rate of the Geiger counter on the supply voltage.
The presence of the plateau greatly facilitates the power of the Geiger counter - it does not require the highly stable high voltage sources that are required for scintillation counters. The length of this plateau for low-voltage meters is 80-100 V. In many Soviet household dosimeters of cooperative origin and in almost all amateur constructions of that time, the meter was powered from a voltage converter based on a blocking generator without any hint of stabilization. The calculation was as follows: with a fresh battery, the voltage at the anode of the meter corresponded to the upper plateau boundary, so that the low plateau boundary reached a high voltage even with a fairly discharged battery.
Any detector of any radiation always has some dark signal recorded when no radiation is incident on the detector. The Geiger-Muller counter is no exception. One of the sources of dark background is the spontaneous emission mentioned above. The second is the radioactivity of the meter itself, which is especially important for meters with a mica window, since natural mica inevitably contains impurities of uranium and thorium. And if the latter practically does not depend on anything and is a constant for a given detector instance, then the background from spontaneous emission depends on the magnitude of the high voltage, temperature, “age” of the counter. Because of this, it becomes a bad idea to supply a meter with unstabilized voltage, which we will use mainly when measuring low levels of radiation: the meter’s own background depends on the supply voltage quite significantly.
The counting rate from its own background reaches a level corresponding to 3-10 μR / h for Geiger counters, that is, it accounts for a significant fraction of the counting rate in a normal radiation environment. The background of mica sensors is especially great - SBT-10, SI-8B, and Beta. So it must be deducted from the measurement results. But for this you need to know it. The reference book does not help here: only maximum values are given there. To measure your own background, you need a lead "house" at least 5 cm thick, while the inner surface must be covered with sheets of copper with a thickness of 2-3 mm and 5 mm plexiglass. The fact is that the “house” will be under shelling of cosmic rays, which make the house itself an X-ray source, mainly in the characteristic lines of lead. And if you make protection only from lead, this is a fluorescent "glow" and "see" the counter - instead of total "darkness". And plexiglass is needed from electrons knocked out by the same cosmic of lead and copper, whose energy is also sufficient for detection by a Geiger counter.
When measuring the background, it should be borne in mind that the lead "house" does not pose any obstacle for cosmic muons. Their flow is ~ 0,015 . For example, through the SBM-20 counter with an effective area of ~ 8 pass 0.12 or 7.2 . Due to the high energy, the registration efficiency of cosmic muons by almost any Geiger counter can be taken as 100%, and this value should be subtracted from the dark background.
If the background is a source of errors at low levels, then the dead time affects at high levels of radiation. The essence of the phenomenon is that immediately after the pulse, the capacity of the counter has not yet been charged to the initial voltage through the load resistance. In addition, in the meter only the discharge went out - but the quenching additive had not yet managed to return to its original state. Therefore, a 150-200 µs counter has a state when it is insensitive to the next particle, after which it gradually restores sensitivity. (pic. 3)
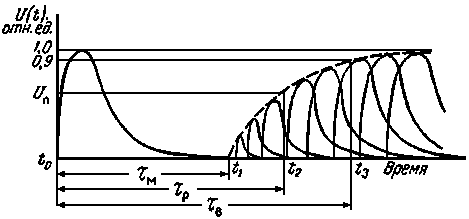
Fig. 3. Dead Time Geiger Counter
The dead time correction is according to the formula:
where m and n, respectively, are the measured and corrected count rates, and - dead time.
With very high levels of radiation in many Geiger counters (it also depends on the rest of the circuit), an unpleasant and dangerous effect occurs: constant ionization prevents individual impulses from forming. The counter starts to continuously “burn” with a constant discharge and the counting rate drops sharply to a very small value. Instead of going off-scale, the dosimeter shows some moderately elevated, if not almost normal numbers. In the meantime, tens and hundreds of X-rays an hour shine around and it would be necessary to run, but you are reassured by the dosimeter's readings. That is why in army dosimeters there is almost always a besides the main sensitive one - the “Doomsday” counter, which is very insensitive, but able to digest thousands of P / h.
Generally speaking, the Geiger counter does not measure the dose rate. We get only the counting rate - how many pulses per minute or second the counter gave. By the dose - the energy absorbed in one kilogram of the human body (or something else) is very far from it. First of all, in connection with the principle of action: the Geiger counter absolutely does not care about the nature of the particle and its energy. Pulses from photons of any energy, beta particles, muons, positrons, protons - will be the same. But the registration efficiency is different.
As I said, the beta radiation Geiger counter registers with efficiency of tens of percent. And gamma-gamma-quanta are only fractions of a percent. And all this is reminiscent of folding meters with kilograms, and even with arbitrarily taken coefficients. In addition, the sensitivity of the counter to gamma radiation varies at different energies (Fig. 4). The dose sensitivity to radiation of different energies can differ by almost an order of magnitude. The nature of this phenomenon is clear: low-energy gamma radiation has a much greater chance of being absorbed by a thin layer of matter, so the lower the energy, the higher the efficiency (until the absorption in the walls of the counter begins to affect). In the high-energy region, on the contrary: with increasing energy, the registration efficiency increases, which is an unusual phenomenon among ionizing radiation detectors.
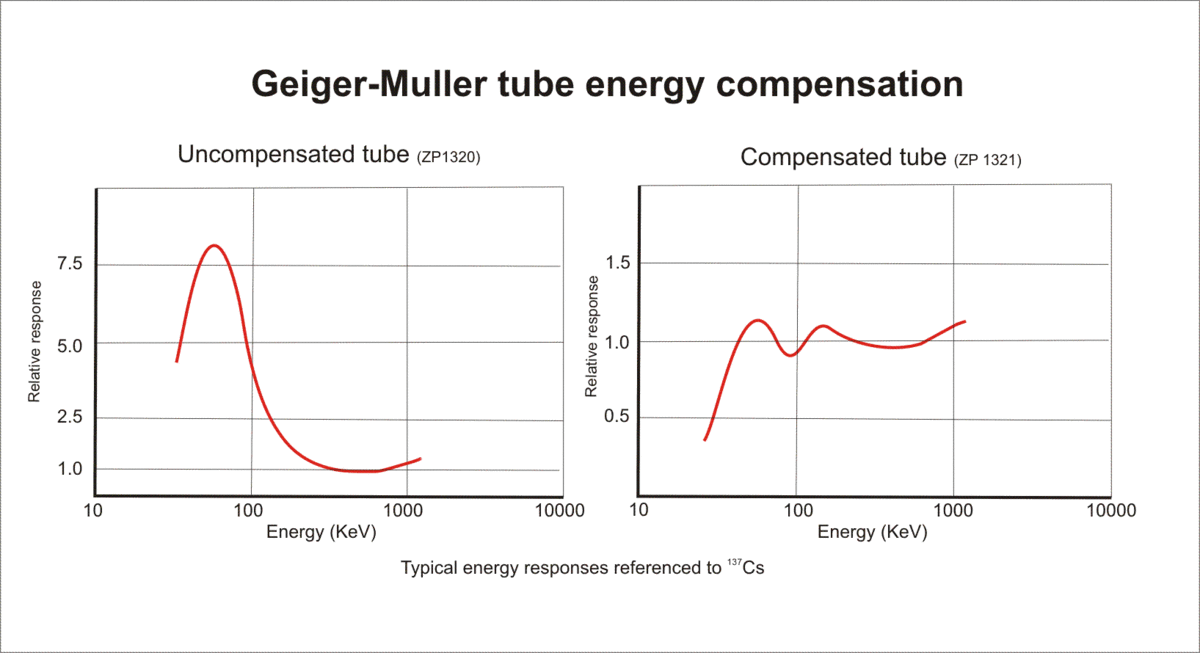
Fig. 4. Energy dependence of the dose sensitivity of the Geiger-Muller counter (left) and the result of its compensation with a filter.
Fortunately, at high energies (above 0.5-1 MeV), the efficiency of a Geiger counter to gamma radiation is almost proportional to energy. So, the energy dependence of the dose sensitivity there is small. A hump at low energies is easy to remove with a filter of about 0.5 mm thick lead. The thickness of the filter is chosen so that at an energy corresponding to the maximum sensitivity of the detector (this is 50-100 keV, depending on the thickness of the detector input window), the absorption ratio would be the value of this peak. The more energy, the less absorption in lead, and at 500-1000 keV, where the sensitivity of the detector is aligned itself, it is almost imperceptible.
A more accurate correction can be achieved using a multi-layer filter of different metals, which must be selected to a specific counter.
Such a filter reduces the “stroke with rigidity” to a value of 15–20% over the entire range of 50–3000 keV and turns the display meter (ok, search radiometer indicator) into a dosimeter.
Such a filter is usually made removable because it makes the sensor insensitive to alpha and beta radiation.
In general, this is all you need to know about the Geiger-Muller counter, the designer of devices based on it. As you can see, the device is really simple, although a number of subtleties are available. In the next series, we will construct something useful based on it.

The heart of our device will be a Geiger counter. We know, of course, that this detector has a lot of flaws and in general “the device must be scintillation”, but the scintillation radiometer is much more complicated and I have the next post for it. Moreover, the Geiger-Muller counter has a number of undeniable advantages.
So, let's begin.
Detector
So, the Geiger-Muller counter. (Fig. 1) The simplest device consisting of two electrodes placed in a gaseous medium at low pressure is a cathode having a large area and an anode in the form of more or less thin wire creating a local field of great intensity. in which the process of multiplication of ions develops, due to which a single ion pair can cause a powerful avalanche of ionization and the ignition of an independent discharge.
')

Fig. 1. Geiger-Muller counter. 1 — anode, 2 — cathode, 3 — balloon, 4 — cathode lead, 5, 6 — springs tightening the cathode filament.
In fact, the counter works like a cold cathode thyratron, only the discharge in it is ignited by ionization, caused not by a pulse from the grid, but by a charged particle flying through the gas. After the discharge has caught fire, it must be extinguished either by removing the voltage from the anode, or ... Or it will go off itself. But for this purpose, it is necessary to introduce something into the gas medium of the meter, which under the action of the discharge will turn into a form that will make the gas opaque to ultraviolet radiation and because of this one of the factors for maintaining an independent discharge - photoelectric emission - will disappear. There are two such additives: alcohol and halogens (chlorine, bromine and iodine). The first in the discharge decomposes, turning, roughly speaking, into soot, and then does not turn back into alcohol, and after a few tens of thousands of pulses will end and the meter ends. And halogens become molecular atomic from, and the process is reversible. They also end - due to the fact that atomic halogens easily react with everything, including the counter walls, but more often they have time to recombine with each other, therefore halogen counters are much more durable, withstanding billions of pulses. We are primarily interested in halogen meters, because:
a) they are more durable
b) they operate at 400-500 V, and not at one and a half thousand, like alcohol,
c) they are simply the most common.
In Table 1, I listed several common Geiger counters and their main parameters.
Table 1.
The main parameters of some Geiger-Muller counters.

Notes: 1 - sensitivity to alpha radiation is not regulated; 2 - small-scale counter, the data on it is scarce.
Sensitivity
When choosing a Geiger counter for our dosimeter, you must first look at its sensitivity. After all, it is unlikely that you want a device that will show something only where Kuzkina Mother exploded a couple of hours ago. But there are plenty of such meters, and for their almost complete uselessness for the average man, they are very cheap. These are all sorts of SI-3BG, SI-13G and other “doomsday counters” standing in army dosimeters for work at the upper limit of measurements. The more sensitive the counter, the more pulses per second it will give at the same level of radiation. The classic SBM-20 counter (also known as the earlier issues was called STS-5), which was traditionally put into all reorganization-post-Chernobyl “ratchets”, with a natural background of 12 μR / h gives about 18 pulses per minute. From this figure it is convenient to dance, considering the sensitivity of the counter in the "SBM-20".
What gives us the sensitivity of the counter? Accuracy and speed of reaction. The fact is that the particles of radioactive radiation arrive to us not according to the schedule, but as it should be, and some of them will miss the counter, but from some of them will work (from photons of gamma radiation - approximately from one of several hundreds). So the pulses from the Geiger counter (and from any counting radiation detector) come at absolutely random times with unpredictable intervals between them. And counting the number of pulses in one minute, another, the third - we get different values. And the standard deviation of these values, that is, the error in determining the counting rate, will be proportional to the square root of the number of recorded pulses. The greater the number of pulses, the smaller will be the relative (as a percentage of the measured value) error in their counting:
.
When we have a detector — the mentioned “reference” SBM-20, and the counting time — 40 seconds (this was done in simple household dosimeters, directly showing the number of counted pulses as a dose rate level in μR / h), on a natural background the number of pulses is ~ 10 pieces. And this means that the standard deviation is about three. And the error at 95% confidence level is twice as large, that is, 6 pulses. Thus, we have a sad picture: the dosimeter readings of 10 μR / h mean that the dose rate is somewhere from 4 to 16 μR / h. And we will be able to talk about the detection of an anomaly only when the dosimeter shows a deviation of three sigmas, that is, more than 20 μR / h ...
To increase accuracy, you can increase the counting time. If we make it three minutes, that is, four times more, we will quadruple the number of pulses, which means we double the accuracy. But then we will lose the response of the device to short bursts of radiation, for example, at the “Your Excellency” that passed by you after scintigraphy or radioiodine therapy or vice versa, when you pass by the radio base past the SPD clock. And taking four times more sensitive detector (4 parallel-connected SBM-20, one SBM-19, SBT-10 or SI-8B) and leaving the same measurement time, we will increase the accuracy and maintain the speed of the reaction.
Alpha, beta, gamma and meter design
Alpha radiation is delayed by a piece of paper. Beta radiation can be shielded with a plexiglass sheet. And from hard gamma radiation you need to build a wall of lead bricks. This is probably all know. And all this has a direct bearing on Geiger counters: in order for him to sense the radiation, it is necessary that it at least penetrate inside. And it should not fly right through, like a neutrino through the Earth.
The SBM-20 type counter (and its older brother the SBM-19 and the younger ones of the SBM-10 and the SBM-21) have a metal casing, in which there are no special entrance windows. From this it follows that there is no question of any sensitivity to alpha radiation. Beta rays he feels quite well, but only if they are tough enough to get inside. This is somewhere from 300 keV. But he feels the gamma radiation, starting with a couple of dozen keV.
And the SBT-10 and SI-8B counters (as well as the new-fashioned and inaccessible because of the scrap prices Beta-1, 2 and 5) instead of a solid steel shell have an extensive window of thin mica. Beta particles with energies above 100-150 keV are able to penetrate through this window, which makes it possible to see carbon 14 pollution, which is completely invisible to steel counters. Also, a window of mica allows the counter to feel alpha particles. True, in relation to the latter, it is necessary to look at the thickness of the mica specific meters. So, SBT-10 with its thick mica practically does not see it, while Beta-1 and 2 have thinner mica, which makes the registration efficiency of alpha particles of plutonium-239 about 20%. SI-8B - somewhere in the middle between them.
And now with regard to the passage through. The fact is that the alpha and beta particles of the Geiger counter registers almost everything that could penetrate inside. But with gamma rays everything is sad. In order for a gamma quantum to trigger a pulse in a counter, it must knock an electron out of its wall. This electron must overcome the thickness of the metal from the point where the interaction occurred, to the inner surface, and therefore the “working volume” of the detector, where it interacts with the photons of gamma radiation, is the thinnest, several microns, layer of metal. From this it is clear that the efficiency of the counter for gamma radiation is very small — a hundred or more times less than for beta radiation.
Nutrition
For the Geiger counter operation requires high voltage power. Typical Soviet-Russian halogen devices require a voltage of about 400 V, many western meters are rated for 500 or 900 V. Some meters require voltages up to one and a half kilovolts - these are old meters with alcohol quenching of the type MS and BC, X-ray counters for X-ray analysis, neutron . They will not interest us much. Power is supplied to the meter through the ballast resistance of a few megaohms - it limits the current pulse and reduces the voltage at the counter after the pulse, facilitating damping. The magnitude of this resistance is given in the reference data for a specific device — its too small a magnitude shortens the life of the detector, and too much increases the dead time. It can usually be taken at about 5 megohms.
When the voltage increases from zero, the Geiger counter first works like an ordinary ionization chamber, and then as a proportional counter: each of the pairs of ions that were formed during the passage of a particle produces small ions, increasing the ion current hundreds and thousands of times. At the same time, very weak impulses measured by millivolts can already be detected on the load resistance in the counter circuit. As the voltage rises, avalanches become more and more, and at some point the strongest of them begin to support themselves, igniting an independent discharge. At this moment, instead of weak millivolt pulses from avalanches passing through the interelectrode space and disappearing at the electrodes, gigantic, with an amplitude of several tens of volts, appear! And their frequency grows rapidly with increasing voltage, until each avalanche starts to cause a flash of discharge. Obviously, with a further increase in voltage, the counting rate should stop growing. So it happens: a plateau is observed on the dependence of sensitivity on voltage.
Nevertheless, the increase in voltage does not leave the counting rate unchanged: a discharge may arise just as a result of spontaneous emission. And with increasing voltage, the probability of such a discharge only increases. Therefore, the plateau is oblique, and starting from a certain voltage, the counting rate begins to grow rapidly, and then the discharge becomes continuous. In this mode, of course, the meter not only fails to fulfill its function, but also quickly fails.

Fig. 2. The dependence of the counting rate of the Geiger counter on the supply voltage.
The presence of the plateau greatly facilitates the power of the Geiger counter - it does not require the highly stable high voltage sources that are required for scintillation counters. The length of this plateau for low-voltage meters is 80-100 V. In many Soviet household dosimeters of cooperative origin and in almost all amateur constructions of that time, the meter was powered from a voltage converter based on a blocking generator without any hint of stabilization. The calculation was as follows: with a fresh battery, the voltage at the anode of the meter corresponded to the upper plateau boundary, so that the low plateau boundary reached a high voltage even with a fairly discharged battery.
Background and Dead Time
Any detector of any radiation always has some dark signal recorded when no radiation is incident on the detector. The Geiger-Muller counter is no exception. One of the sources of dark background is the spontaneous emission mentioned above. The second is the radioactivity of the meter itself, which is especially important for meters with a mica window, since natural mica inevitably contains impurities of uranium and thorium. And if the latter practically does not depend on anything and is a constant for a given detector instance, then the background from spontaneous emission depends on the magnitude of the high voltage, temperature, “age” of the counter. Because of this, it becomes a bad idea to supply a meter with unstabilized voltage, which we will use mainly when measuring low levels of radiation: the meter’s own background depends on the supply voltage quite significantly.
The counting rate from its own background reaches a level corresponding to 3-10 μR / h for Geiger counters, that is, it accounts for a significant fraction of the counting rate in a normal radiation environment. The background of mica sensors is especially great - SBT-10, SI-8B, and Beta. So it must be deducted from the measurement results. But for this you need to know it. The reference book does not help here: only maximum values are given there. To measure your own background, you need a lead "house" at least 5 cm thick, while the inner surface must be covered with sheets of copper with a thickness of 2-3 mm and 5 mm plexiglass. The fact is that the “house” will be under shelling of cosmic rays, which make the house itself an X-ray source, mainly in the characteristic lines of lead. And if you make protection only from lead, this is a fluorescent "glow" and "see" the counter - instead of total "darkness". And plexiglass is needed from electrons knocked out by the same cosmic of lead and copper, whose energy is also sufficient for detection by a Geiger counter.
When measuring the background, it should be borne in mind that the lead "house" does not pose any obstacle for cosmic muons. Their flow is ~ 0,015 . For example, through the SBM-20 counter with an effective area of ~ 8 pass 0.12 or 7.2 . Due to the high energy, the registration efficiency of cosmic muons by almost any Geiger counter can be taken as 100%, and this value should be subtracted from the dark background.
If the background is a source of errors at low levels, then the dead time affects at high levels of radiation. The essence of the phenomenon is that immediately after the pulse, the capacity of the counter has not yet been charged to the initial voltage through the load resistance. In addition, in the meter only the discharge went out - but the quenching additive had not yet managed to return to its original state. Therefore, a 150-200 µs counter has a state when it is insensitive to the next particle, after which it gradually restores sensitivity. (pic. 3)

Fig. 3. Dead Time Geiger Counter
The dead time correction is according to the formula:
where m and n, respectively, are the measured and corrected count rates, and - dead time.
With very high levels of radiation in many Geiger counters (it also depends on the rest of the circuit), an unpleasant and dangerous effect occurs: constant ionization prevents individual impulses from forming. The counter starts to continuously “burn” with a constant discharge and the counting rate drops sharply to a very small value. Instead of going off-scale, the dosimeter shows some moderately elevated, if not almost normal numbers. In the meantime, tens and hundreds of X-rays an hour shine around and it would be necessary to run, but you are reassured by the dosimeter's readings. That is why in army dosimeters there is almost always a besides the main sensitive one - the “Doomsday” counter, which is very insensitive, but able to digest thousands of P / h.
From count rate to dose. Stroke with rigidity and other bad things
Generally speaking, the Geiger counter does not measure the dose rate. We get only the counting rate - how many pulses per minute or second the counter gave. By the dose - the energy absorbed in one kilogram of the human body (or something else) is very far from it. First of all, in connection with the principle of action: the Geiger counter absolutely does not care about the nature of the particle and its energy. Pulses from photons of any energy, beta particles, muons, positrons, protons - will be the same. But the registration efficiency is different.
As I said, the beta radiation Geiger counter registers with efficiency of tens of percent. And gamma-gamma-quanta are only fractions of a percent. And all this is reminiscent of folding meters with kilograms, and even with arbitrarily taken coefficients. In addition, the sensitivity of the counter to gamma radiation varies at different energies (Fig. 4). The dose sensitivity to radiation of different energies can differ by almost an order of magnitude. The nature of this phenomenon is clear: low-energy gamma radiation has a much greater chance of being absorbed by a thin layer of matter, so the lower the energy, the higher the efficiency (until the absorption in the walls of the counter begins to affect). In the high-energy region, on the contrary: with increasing energy, the registration efficiency increases, which is an unusual phenomenon among ionizing radiation detectors.

Fig. 4. Energy dependence of the dose sensitivity of the Geiger-Muller counter (left) and the result of its compensation with a filter.
Fortunately, at high energies (above 0.5-1 MeV), the efficiency of a Geiger counter to gamma radiation is almost proportional to energy. So, the energy dependence of the dose sensitivity there is small. A hump at low energies is easy to remove with a filter of about 0.5 mm thick lead. The thickness of the filter is chosen so that at an energy corresponding to the maximum sensitivity of the detector (this is 50-100 keV, depending on the thickness of the detector input window), the absorption ratio would be the value of this peak. The more energy, the less absorption in lead, and at 500-1000 keV, where the sensitivity of the detector is aligned itself, it is almost imperceptible.
A more accurate correction can be achieved using a multi-layer filter of different metals, which must be selected to a specific counter.
Such a filter reduces the “stroke with rigidity” to a value of 15–20% over the entire range of 50–3000 keV and turns the display meter (ok, search radiometer indicator) into a dosimeter.
Such a filter is usually made removable because it makes the sensor insensitive to alpha and beta radiation.
***
In general, this is all you need to know about the Geiger-Muller counter, the designer of devices based on it. As you can see, the device is really simple, although a number of subtleties are available. In the next series, we will construct something useful based on it.
Source: https://habr.com/ru/post/430198/
All Articles