Memcached clustering and caching key selection
A series of posts under the general title “Web, caching and memcached” continues. In the first, we talked about memcached, its architecture, and its possible use.
Today we will talk about:
The following post will be devoted to atomic operations and counters in memcached .
Suppose we have already seen that using memcached for caching is the right decision. The first task that confronts us is the selection of a key for each cache. The key in memcached is a string of limited length, consisting of a limited set of characters (for example, spaces are not allowed). The caching key must have the following properties:
Of course, we could build a key for each sample by ourselves, for example,
')
You can use the following option (example for PHP): if there is a point in the code through which all calls to the database pass, and any call is fully described (contains all the request parameters) in a certain
Such a key undoubtedly satisfies the first condition (if
For load balancing and fault tolerance, a cluster of such servers is used instead of a single memcached server. Servers included in the cluster can be configured with different amounts of memory, while the total cache volume will be equal to the sum of the cache volumes of all memcached included in the cluster. The memcached process can be run on a server where the processor is poorly used and the network is not loaded to the limit (for example, on a file server). With a high load on the processor, memcached may not be able to respond quickly enough to queries, which leads to degradation of the service.
When working with a cluster, the keys are distributed across servers, that is, each server processes part of the project's total key array. Fault tolerance follows from the fact that in the event of a failure of one of the servers, the keys will be redistributed to the remaining servers in the cluster. In this case, of course, the contents of the failed server will be lost (see the section "Loss of keys"). If necessary, important keys can be stored not on a single server, but duplicated on several, so you can minimize the consequences of a server crashing due to redundant storage.
With clustering, the key distribution issue becomes topical: how to distribute keys among servers in the most efficient way. To do this, it is necessary to determine the key distribution function, which by key returns the number of the server on which it should be stored (or server numbers if storage is redundant).
Historically, the first distribution function was the module function:
Such a function ensures even distribution of keys across servers, but problems arise when memcached cluster is reconfigured: changing the number of servers leads to the movement of a significant part of the keys across servers, which is equivalent to losing a significant part of the keys.
An alternative to this function is consistent hashing, which, when the cluster is reconfigured, maintains the position of the keys across the servers. This approach was implemented in memcached clients for the first time by developers of the Last.fm service in April 2007.
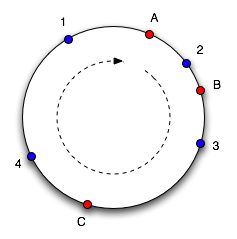
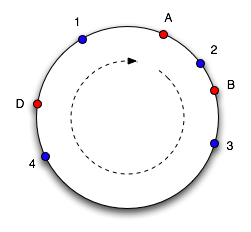
The essence of the algorithm is as follows: we consider a set of integers from 0 to 2 32 , “twisting” the numerical axis into a ring (we glue 0 and 2 32 ). To each server in the pool of memcached servers, we associate a number on the ring (image on the left, servers A, B, and C). The key is hashed to a number in the same range (blue dots 1-4 in the figure), we choose the server at the point closest to the key point in the clockwise direction as the server for storing the key. If the server is removed from the pool or added to the pool, a server point appears or disappears on the axis, as a result of which only a part of the keys are moved to another server. Figure 2 on the right shows the situation when server C was removed from the server pool and a new server D was added. It is easy to see that keys 1 and 2 did not change server bindings, and keys 3 and 4 moved to other servers. In fact, one server is assigned 100-200 points on an axis (proportional to its weight in the pool), which improves the uniform distribution of keys across servers in the event of a change in their configuration.
This algorithm has been implemented in many memcached clients in various programming languages, but the implementation is sometimes different in details, which leads to hash incompatibility. This fact makes consistent hashing inconvenient to use when accessing the same pool of memcached servers from different programming languages. The simplest algorithm with crc32 and module is implemented in all clients in all languages in the same way, which ensures identical hashing of keys across servers. Therefore, if there is no need to access memcached from different clients in different programming languages, the approach with consistent hashing looks more attractive.
Today we will talk about:
- caching key selection;
- memcached clustering and key distribution algorithms.
The following post will be devoted to atomic operations and counters in memcached .
Caching key
Suppose we have already seen that using memcached for caching is the right decision. The first task that confronts us is the selection of a key for each cache. The key in memcached is a string of limited length, consisting of a limited set of characters (for example, spaces are not allowed). The caching key must have the following properties:
- When changing the sample parameters that we cache, the caching key must change (so that we don’t “get” to the old cache with the new parameters).
- According to the sampling parameters, the key must be determined uniquely, i.e. for the same sample, the caching key should be only one, otherwise we risk reducing the efficiency of the caching process.
Of course, we could build a key for each sample by ourselves, for example,
'user_158' to fetch user information with ID 158 or 'friends_192_public_sorted_online' for user friends with ID 192, which are publicly available and, moreover, sorted in the order of the last appearance on the site. Such an approach is fraught with errors and non-compliance with the conditions set forth above.')
You can use the following option (example for PHP): if there is a point in the code through which all calls to the database pass, and any call is fully described (contains all the request parameters) in a certain
$options structure, you can use the following key: $key = md5(serialize($options)) Such a key undoubtedly satisfies the first condition (if
$options changes, the $options $key will necessarily be changed), but the second condition will be met if we use all the data types in $ options “canonically”, i.e. Do not allow the string "1" instead of the number 1 (although in PHP two such values are equal, but their serialized representation is different). The md5 function is used to “compress” data: the memcached key is limited in length, and the serialized representation may be too long.Memcached clustering
For load balancing and fault tolerance, a cluster of such servers is used instead of a single memcached server. Servers included in the cluster can be configured with different amounts of memory, while the total cache volume will be equal to the sum of the cache volumes of all memcached included in the cluster. The memcached process can be run on a server where the processor is poorly used and the network is not loaded to the limit (for example, on a file server). With a high load on the processor, memcached may not be able to respond quickly enough to queries, which leads to degradation of the service.
When working with a cluster, the keys are distributed across servers, that is, each server processes part of the project's total key array. Fault tolerance follows from the fact that in the event of a failure of one of the servers, the keys will be redistributed to the remaining servers in the cluster. In this case, of course, the contents of the failed server will be lost (see the section "Loss of keys"). If necessary, important keys can be stored not on a single server, but duplicated on several, so you can minimize the consequences of a server crashing due to redundant storage.
With clustering, the key distribution issue becomes topical: how to distribute keys among servers in the most efficient way. To do this, it is necessary to determine the key distribution function, which by key returns the number of the server on which it should be stored (or server numbers if storage is redundant).
Historically, the first distribution function was the module function:
f() = crc32() % _ Such a function ensures even distribution of keys across servers, but problems arise when memcached cluster is reconfigured: changing the number of servers leads to the movement of a significant part of the keys across servers, which is equivalent to losing a significant part of the keys.
An alternative to this function is consistent hashing, which, when the cluster is reconfigured, maintains the position of the keys across the servers. This approach was implemented in memcached clients for the first time by developers of the Last.fm service in April 2007.


The essence of the algorithm is as follows: we consider a set of integers from 0 to 2 32 , “twisting” the numerical axis into a ring (we glue 0 and 2 32 ). To each server in the pool of memcached servers, we associate a number on the ring (image on the left, servers A, B, and C). The key is hashed to a number in the same range (blue dots 1-4 in the figure), we choose the server at the point closest to the key point in the clockwise direction as the server for storing the key. If the server is removed from the pool or added to the pool, a server point appears or disappears on the axis, as a result of which only a part of the keys are moved to another server. Figure 2 on the right shows the situation when server C was removed from the server pool and a new server D was added. It is easy to see that keys 1 and 2 did not change server bindings, and keys 3 and 4 moved to other servers. In fact, one server is assigned 100-200 points on an axis (proportional to its weight in the pool), which improves the uniform distribution of keys across servers in the event of a change in their configuration.
This algorithm has been implemented in many memcached clients in various programming languages, but the implementation is sometimes different in details, which leads to hash incompatibility. This fact makes consistent hashing inconvenient to use when accessing the same pool of memcached servers from different programming languages. The simplest algorithm with crc32 and module is implemented in all clients in all languages in the same way, which ensures identical hashing of keys across servers. Therefore, if there is no need to access memcached from different clients in different programming languages, the approach with consistent hashing looks more attractive.
Materials
Source: https://habr.com/ru/post/42972/
All Articles