MIT course "Computer Systems Security". Lecture 16: "Attacks through the side channel", part 2

Massachusetts Institute of Technology. Lecture course # 6.858. "Security of computer systems". Nikolai Zeldovich, James Mykens. year 2014

Computer Systems Security is a course on the development and implementation of secure computer systems. Lectures cover threat models, attacks that compromise security, and security methods based on the latest scientific work. Topics include operating system (OS) security, capabilities, information flow control, language security, network protocols, hardware protection and security in web applications.

Lecture 1: "Introduction: threat models" Part 1 / Part 2 / Part 3
Lecture 2: "Control of hacker attacks" Part 1 / Part 2 / Part 3
Lecture 3: "Buffer overflow: exploits and protection" Part 1 / Part 2 / Part 3
Lecture 4: "Separation of privileges" Part 1 / Part 2 / Part 3
Lecture 5: "Where Security Errors Come From" Part 1 / Part 2
Lecture 6: "Opportunities" Part 1 / Part 2 / Part 3
Lecture 7: "Sandbox Native Client" Part 1 / Part 2 / Part 3
Lecture 8: "Model of network security" Part 1 / Part 2 / Part 3
Lecture 9: "Web Application Security" Part 1 / Part 2 / Part 3
Lecture 10: "Symbolic execution" Part 1 / Part 2 / Part 3
Lecture 11: "Ur / Web programming language" Part 1 / Part 2 / Part 3
Lecture 12: "Network Security" Part 1 / Part 2 / Part 3
Lecture 13: "Network Protocols" Part 1 / Part 2 / Part 3
Lecture 14: "SSL and HTTPS" Part 1 / Part 2 / Part 3
Lecture 15: "Medical Software" Part 1 / Part 2 / Part 3
Lecture 16: "Attacks through the side channel" Part 1 / Part 2 / Part 3

Audience: how to determine x and y first?
')
Professor: for this you have to look at the exhibitor in the binary representation. Suppose I try to calculate the value of c ^1011010 , the degree may consist of a larger number of bits. If we want to do a repeated squaring, then we need to look at the lowest bit - here it is 0.



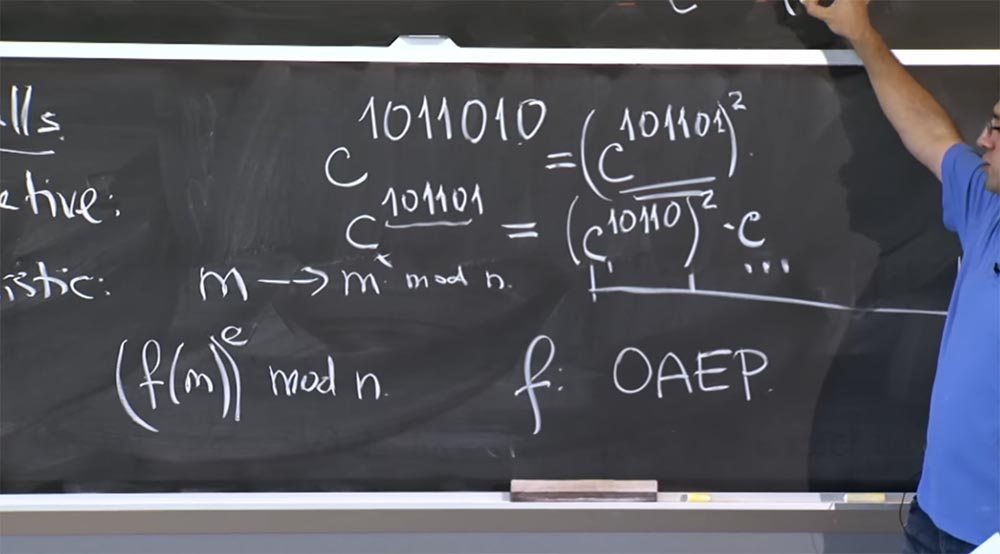
Thus, we have the equality c ^1011010 = (c ¹⁰¹¹⁰¹ ) ²

Next, we need to calculate c ¹⁰¹¹⁰¹ , here we cannot use this rule, because it is not 2x - it will be x plus 1. Therefore, we write this equality:

c ¹⁰¹¹⁰¹ = (c ¹⁰¹¹⁰ ) ² c, because this prefix is ​​101101 = 10110 + 1.

Therefore, we multiply the square by c, so we use it for re-squaring.

For sliding windows, we need to capture more bits from the lower end. If you want to do a “sliding window” trick here instead of extracting one from here, then with this huge table we can take 3 bits at a time, clinging to c7. If we take the first 3 bits of the degree, we get c ¹⁰¹¹⁰¹ = (c ¹⁰¹ ) ⁸ c ¹⁰¹ .

In this case, we really have the same amount of calculations for (c ¹⁰¹ ) ⁸ , but you can see the value of c ¹⁰¹ in the table. And the part in the form (c ¹⁰¹ ) ⁸ says that you are going to use the “sliding windows” to calculate its value.



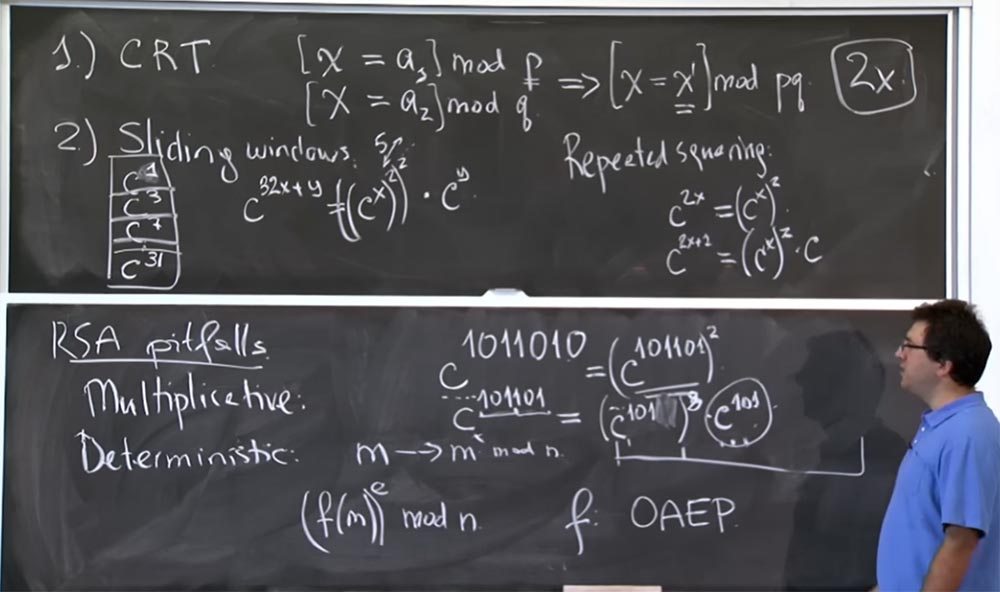
This saves a lot of time, as it allows you to use pre-multiplied values. 10 years ago, it was believed that a table of values ​​up to 32 degrees is the optimal plan in terms of computational efficiency, because there is some kind of compromise, right? You spend time creating this table, but it should not be too large if you are not going to use some records often. Suppose if you create a table of values ​​up to c ⁵⁰⁰ degrees, but you are not going to use exponents with a value greater than 128, then you just waste your time.

Audience: Is there a reason not to create such a giant table in advance? That is, to calculate the values ​​of a limited number of degrees that can be dispensed with in calculations?

Professor: if you do not want to make volume calculations in advance ... well, there are two things here. One is that then you must have a code to check whether the required entry is filled in the table or not, and this will probably reduce the accuracy of prediction of the branches of the CPU process. In this case, in general, the processor will work more slowly, because it will have to check whether there is a necessary entry in the table. The second thing, which is somewhat annoying, may be the leakage of table entries through various side channels, namely through cache access patterns. So if you have some other process running on the same processor, you can see which cache addresses are being removed from the cache or are slowing down because someone has access to the c ³ entry or the c ³¹ entry. And the more this table becomes, the easier it is to determine which exponent bits are used when creating the RSA key.

This giant table is able to tell which cache address was lost for the processor, that is, indicates that the encryption process should have access to this entry in the table. In turn, this tells you that a given sequence of bits appears in the exponent of your secret key. Therefore, I assume that mathematically you can fill this table as much as you need, but in practice you do not want it to turn out to be gigantic in size. In addition, you will not be able to effectively use huge table entries. It is much more useful to use the records of a relatively small table again, for example, to calculate c ^7, you can use the value c ³ twice and so on.

So, this is what RSA optimization is about by means of re-squaring and “sliding window”. I don’t know if they are still using this “sliding window” size, but in any case it speeds up the calculation process, because otherwise you would have to square each bit of the exponent and then multiply by each bit. Therefore, if you have a 500-bit exponent, then you would have to perform 500 squaring and about 256 multiplications per c. With the “sliding windows” you will still have to make 512 squaring, because you cannot avoid it, but the number of multiplications by c will decrease from 256 to about 32 by using records from the table.

This is the general optimization plan, which speeds up the calculation process by about one and a half times. This is a fairly simple optimization. There are two clever tricks with numbers to make the multiplication process more efficient.

The first is the Montgomery transformation, in a second we will see why this is especially important for us. This optimization is trying to solve for us the problem, which is that each time we multiply, we get a number that continues to grow and grow. In particular, both in the “sliding windows” and in the repeated quadration, you actually multiplied 2 numbers together when you raised c to the power of y.

The problem is that if the input data c ^x and c ^y for multiplication was the size of, say, 512 bits each, then the size of the multiplication result will be 1000 bits. After that, you take this 1000-bit result and again multiply it by something like 512 bits, it becomes 1500, 2000, 2500 bits in size and everything grows and grows.

However, you do not want this, because multiplication increases the order of the multiplied numbers. Because of this, we have to keep the size of our number as small as possible, mostly equal to 512 bits, because all these calculations are mod p or mod q.

We can reduce this number, let's say we want to calculate (((c ^x ) ² ) ² ) ² . What you could do is, for example, calculate cx modulo p, then square it again modulo p and square again modulo p. This method is relatively good, as it allows us to keep the size of our number within 512 bits, that is, as little as we can get. This is good in the sense of reducing the size of the numbers that we need to multiply, but in fact the operation with this module p significantly increases the cost of the calculation.



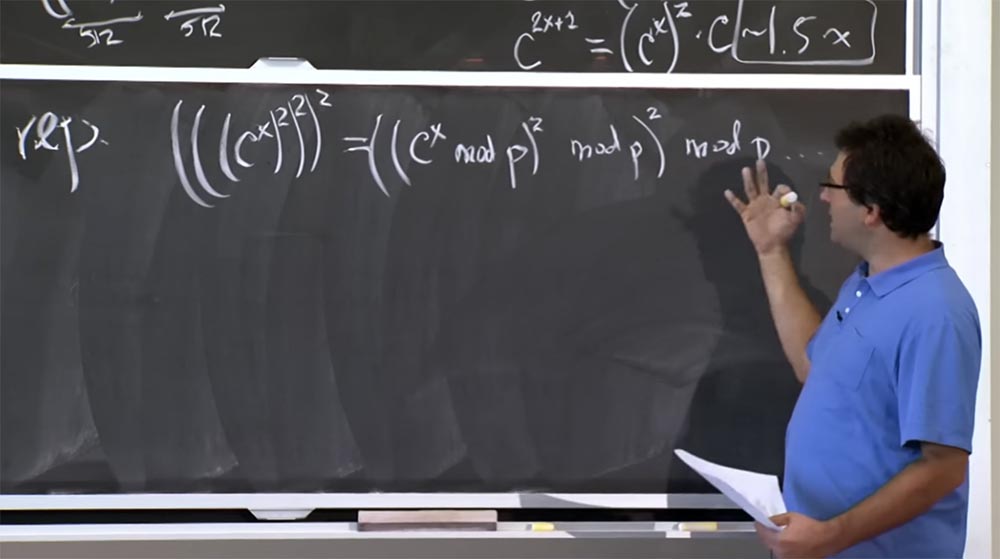
Because the way you get mod p is to divide. And division is worse than multiplication. I will not list the algorithms for division, but this is very slow. Usually you try to avoid division operations as much as possible, because this is not simple programming. The fact is that you need to use some approximation algorithms, Newton's methods, and the like, and all this will slow down the computation process.

Multiplication is much more profitable, but using mod p or mod q operations to reduce the size of numbers is more expensive than multiplication. I will show you how to avoid this and how to do quick calculations using the Montgomery transform.

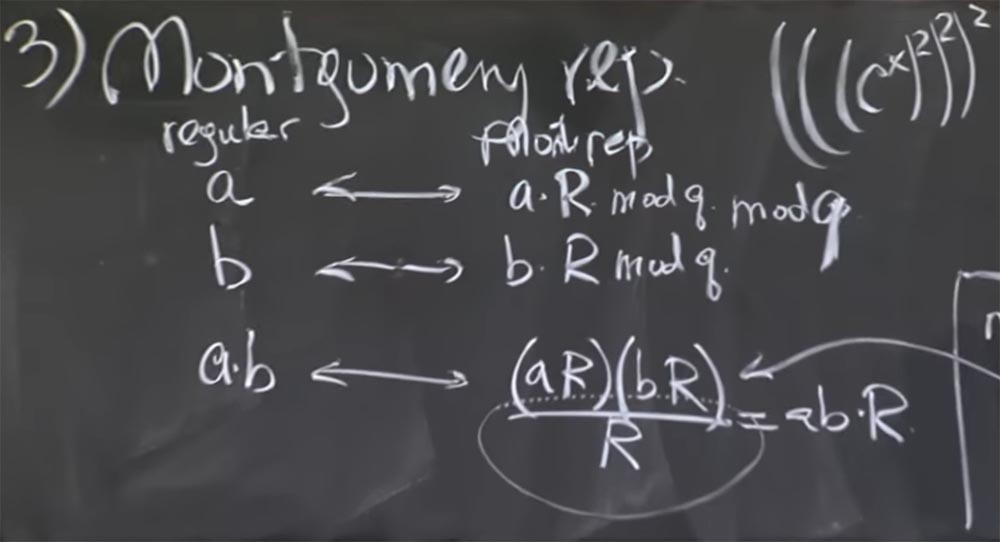
The basic idea is to represent the integers you are going to multiply in the form of the Montgomery transform. In fact, it is very easy. To do this, we simply multiply our number and by some magical value R. In a second I will tell you what it is. But let's first find out what happens here when we choose an arbitrary value of R.

So, we take 2 numbers, a and b, and convert them into a Montgomery representation, multiplying each by R. Then the product of a and b in the Montgomery transformation will look like this:

ab <-> (aR) (bR) / R = abR

That is, you multiply aR by bR and get the product ab by R squared. Now we have two R's, which is a bit annoying, but you can divide it by R. As a result, we get the product of ab by R. It's a little unclear why we needed to multiply this number once more. Let's first find out if this is correct, and then we will understand why it will be faster.
This is correct in the sense that it is very easy. If you want to multiply some numbers, then they need to be multiplied by this value of R and get the Montgomery transform. Each time we multiply these 2 numbers, we have to divide them by R, and then look at the resulting form of a transformation of the form abR. Then, when we finish squaring, multiplication, and all these things, we will return to the normal, usual form of the result, simply dividing by R for the last time.



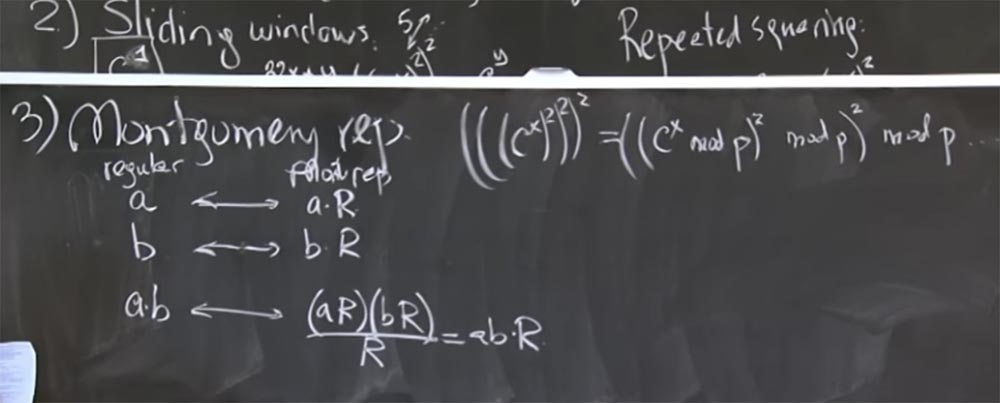
Now consider how to choose the most appropriate number for R to make division by R a very fast operation. And the great thing here is that if the division into R is very fast, when it is a small number, and we don’t have to do this mod q too often. In particular, aR, let's say, will also be about 500 bits in size, because all of this is in fact mod p or mod q. Thus, aR is 500 bits, bR will also be 500 bits, so the product (aR) (bR) will be 1000 bits. R will also be a convenient 500-bit number, the size of p. And if we can make the division operation fast enough, then the result of ab will also be approximately a 500-bit number, so that we can multiply without the need to do additional division. The division into R is much more profitable and gives us the result of small size, which avoids the use of mod p in most situations.

So, what is this strange number R that I’m talking about all the time? It has a value of 2 to 512 degrees:

R = ^2,512

It will be 1 and a bunch of zeros, so it’s easy to multiply by such a number, because it will be enough just to add a bunch of zeros to the result. The division can also be simple if the low-order bits of the result are zero. So if you have a value from a pile of bits, accompanied by 512 zeros, then dividing it by 2 to 512 degrees will be very simple - you just drop zeros on the right side, and this is a completely correct division operation.

A minor problem is that we don’t actually have zeros on the right side when you do this multiplication. We have real 512-bit numbers using all 512 bits.

The product (aR) to (bR) is also a real number on the order of 1000 bits, so we cannot just discard the lower bits. But a reasonable approach is based on the fact that the only thing that worries us is the mod p value. Thus, you can always add several p to this value without changing its equivalent mod p. As a result, we can add multiple p values ​​so that all low bits become zeros. Let's look at some simple examples. I am not going to write out 512 bits on the blackboard, but I will give only a short example.

Suppose that in our situation R = 2 ⁴ = 10000. This is a much smaller size than is found in reality. Let's see how this Montgomery transformation will work. We will try to calculate mod q, where q = 7. In binary form, q = 7 is (111).

Suppose further that we have produced some multiplication (aR) (bR), and in the binary representation the result is 11010, that is, this will be the value of the product (aR) (bR). How do we divide it by R?

Obviously, not all four low bits are zeros, so we cannot just separate them, but we can add multiples of q. In particular, we can add 2 times in q, with 2q = 1110 in binary representation. As a result of the addition, we get 101000, I hope I did everything right.



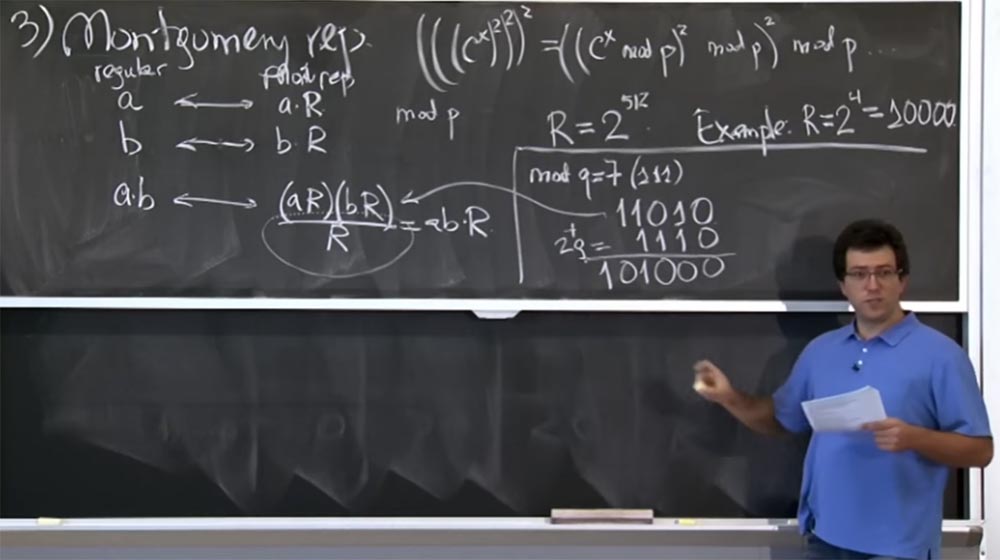
So we got the sum (aR) (bR) + 2q. In fact, we do not care about + 2q, because all we care about is the value of mod q. Now we are closer to the goal, because we have three zeros on the right. Now we can add some more q. Let's say this time it will be 8q, which will be 111000. Add up our lines again and get 1100000. Now we have the original (aR) (bR) + 2q + 8q = 1100000. Finally, we can very easily divide this thing by R, simply dropping four low zeros.



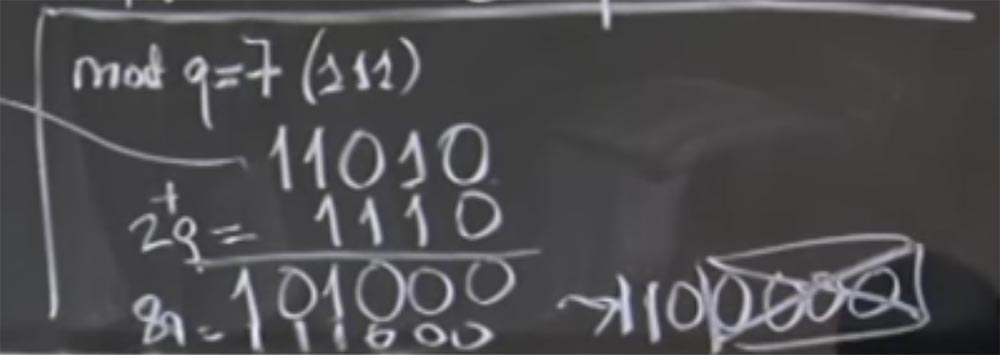
Audience: the product (aR) (bR) will always end with 1024 zeros?

Professor: No, and I will explain what the confusion may be. Let's say the number a is 512 bits, we multiplied it by R and got a 1000-bit number. In this case, you are right, aR is a number in which high bits are a, and low bits are all zeros. But then we do mod q to make it smaller. Therefore, the size of 1024 bits in the general case is an accident, since this number has these low zeros only at the first conversion, but after you do several multiplications, it will be arbitrary bits.

In order not to mislead you, I had to write mod q here after aR and after bR — so I add it — and calculate this mod q as soon as you do the conversion to reduce the value.



The initial transformation is quite laborious, or at least as expensive as normal modulation during multiplication. It's cool that you pay this price once when you do a Montgomery transform, and then, instead of converting it back at every step of the calculation, you just keep it in the form of a Montgomery representation.
Remember that for a exponentiation that has 512 bits, you have to do more than 500 multiplications, because we have to do at least 500 squaring and some more actions. So you do mod q twice and then get a lot of simple division operations if you stay in this form of representing numbers. And at the end you divide by R to return to this form ab.

So, instead of doing mod q q 500 times for each multiplication step, you do mod q twice and then continue to do these divisions of R with minimal cost.
Audience: when you add multiples of q, and then divide by R, do we get a remainder?
Professor: mod q actually means the remainder when you divide by q. Simply put, x + yq mod q = x. In this case, there is another useful feature - this is that all modules are prime numbers. This is as true as the fact that if you have (x + yq / R) mod q, then it is x / R mod q.



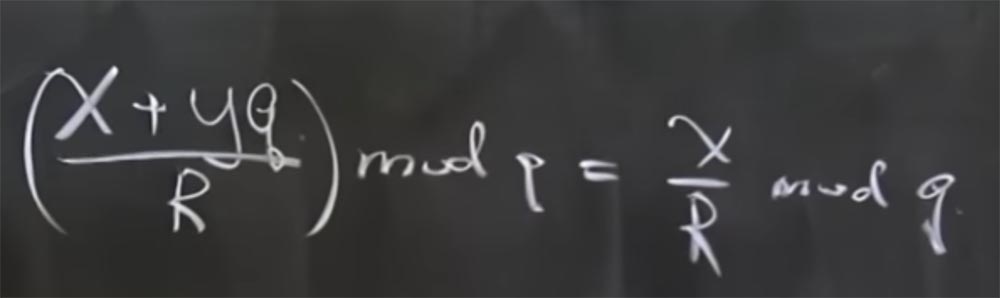
The reason for considering this is that in modular arithmetic there are no real division operations, it is just an invert. In fact, this means that if we have (x + yq) multiplied by the inverted R calculated by the mod q, then it is equal to the sum of two products: the product x by the inverted R by mod q and the product yq by the inverted R mod q. And the last term is reduced, because it is something multiplied by q.



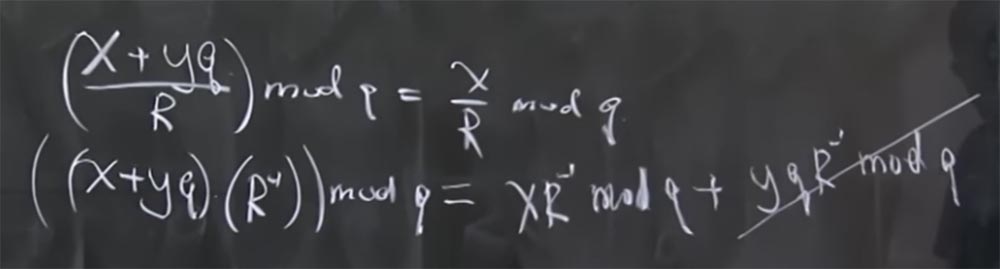
For things like summation of 2q, 8q, and so on, there is a formula that speeds up the calculation process. I did this gradually, first calculating 2q, then 8q, and so on, but in the lecture materials there is a complete formula that I can use, I just don’t want to waste time writing it on the blackboard. It allows you to calculate how many times the q value you need to add, so that all the low-order bits turn into 0. Then it turns out that in order to make a division by R, you just need to calculate this magic multiple of q, add it, then drop the low zero bits, and it will return your number to 512 bits no matter what size of result you got.

But there is one subtlety. The only reason we talk about this is something funny happening here that allows us to find out information about timings. In particular, although we divided it into R, we still know that the result will be about 512 bits. But it can still be more than q, because q is not a 512-bit number, it can be a little less than R.

So it may be that after we do this profitable division by R, we may need to subtract q again, because we get something small, but still not small enough. So there is a chance that after this division we may have to subtract q again. And this subtraction can be used as part of an attack, because the subtraction operation adds computation time.



And someone found out - not these guys, but someone in a previous work - that there is a chance to do something called extra reduction, or an additional reduction. This probability depends on a particular value, which is raised to a power. So, if you calculate xd mod q, the likelihood of an additional reduction at some point in time for computing this value will be x mod q divided by 2R. I will separate this expression from the rest of the calculations.



Depending on whether the value of x mod q is large or small, you will have more or less of these additional cuts. And all this happens at the decryption stage, because when decrypting the server will calculate cd.



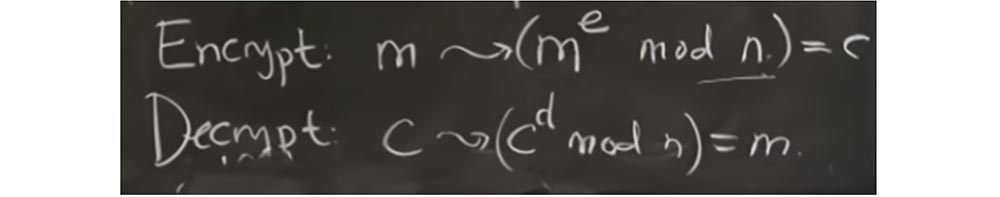
This suggests that extra reduction will be proportional to how close X or, in this case, s, to the value of q.



This is dangerous because the attacker must select the input data c, and the number of extra reduction will be proportional to how close c to one of the factors is q. It’s as if you can tell if you’ve approached a q value or overshot. In this case, a situation suddenly arises when there is no extra reduction, probably because X mod q is very small, and X = q + έ, and this is a very small value. This is part of the attack in the method of determining the timings, which we will talk about in a second. I have no evidence that this is true, but, in any case, these additional reductions of extra reduction work just like this.

Audience: What happens if you do not make this additional reduction?

Professor: what happens if you do not do this extra reduction? , , , . , . , , extra reduction, , , . , . , , mod q. , , , . , mod q , , .

, . , - , . — , . , - , extra reduction .

, . , OpenSSL, , . , mod q . , , .

, , , , a b. — 512- . , 32- , , 64- ? ?



- ? , , a b .

, , 512 , 64- , 32- . a : a ₁ a ₀ , a ₀ , a ₁ — . b – b ₁ b ₀ .

ab 3- : a ₁ b ₁ , a ₀ b ₀ , a ₁ b ₀ + a ₀ b ₁ . .



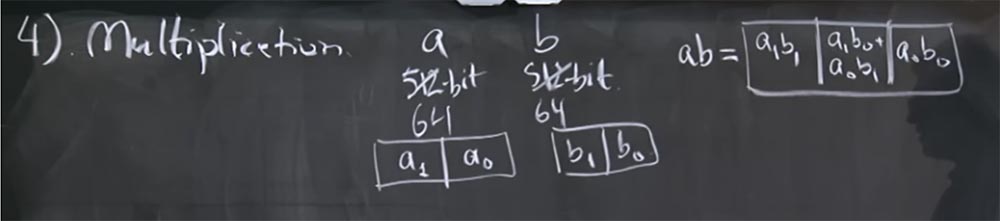
55:00

MIT course "Computer Systems Security". 16: « », 3


Full version of the course is available here .

Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending to friends, 30% discount for Habr users on a unique analogue of the entry-level servers that we invented for you: The whole truth about VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps from $ 20 or how to share the server? (Options are available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps until December for free if you pay for a period of six months, you can order here .

Dell R730xd 2 times cheaper? Only we have 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV from $ 249 in the Netherlands and the USA! Read about How to build an infrastructure building. class c using servers Dell R730xd E5-2650 v4 worth 9000 euros for a penny?