Julia and phase portraits of dynamic systems

We continue to master the young and promising general-purpose language Julia . But first, we need just the very narrow possibility of application - for solving typical problems of physics. This is the most convenient tactic for mastering the tool: in order to fill our hands, we will solve pressing problems, gradually increasing complexity and finding ways to make our lives easier. In short, we will solve diffs and build graphs.

To begin with, download the Gadfly graphics package, and immediately the full version of the developer, so that it works well with our Julia 1.0.1. We drive in our REPL, JUNO or Jupyter notebook:

using Pkg pkg"add Compose#master" pkg"add Gadfly#master" 

Not the most convenient option, but while waiting for the update PlotlyJS, you can compare and try.

You also need a powerful tool for solving differential equations. DifferentialEquations

 ]add DifferentialEquations #     

This is the most extensive and supported package, providing a lot of methods for solving difures. Now proceed to the phase portraits.

The solutions of ordinary differential equations are often more conveniently depicted in a manner not usual. $$$y ^ 1 (t), ..., y ^ L (t)$, and in the phase space , along the axes of which the values ​​of each of the functions found are deposited. The argument t is included in the graphs only parametrically. In the case of two ODEs, such a graph, the phase portrait of the system, is a curve on the phase plane and is therefore particularly visual.

Oscillator

Dynamics of harmonic oscillator with attenuation $$$\ gamma$described by the following system of equations:

and regardless of the initial conditions (x0, y0), it comes to a state of equilibrium, a point (0,0) with a zero deflection angle and zero speed.

With $$$\ gamma = 0$the decision takes the form peculiar to the classical oscillator.

 using DifferentialEquations, Gadfly #     -    function garmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) A = [0 1 -ω^2 γ] syst(u,p,t) = A * u # ODE system u0 = [x0, y0] # start cond-ns tspan = (0.0, 4pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end 

Let's sort the code. The function takes the values ​​of the frequency and attenuation parameter, as well as the initial conditions. The nested syst () function sets the system. In order to come out single-line, they used matrix multiplication. The solve () function accepting a huge number of parameters is configured very flexibly to solve a problem, but we only indicated the solution method — Runge-Kutta 4 ( there are many more ), the relative error, and the fact that not all points need to be saved, but only every fourth . The response matrix is ​​stored in the variable sol , and sol.t contains the vector of time values, and sol.u contains the solutions of the system at these times. All this is quietly drawn in Plots , and for Gadfly it will be necessary to complete the answer in a matrix more comfortably. We do not need times, so we only return solutions.

Construct a phase portrait:

 Ans0 = garmosc() plot(x = Ans0[:,1], y = Ans0[:,2]) 

Among the high-order functions, broadcast(f, [1, 2, 3]) is particularly noticeable for us, which alternately substitutes the values ​​of the array [1, 2, 3] to the function f . A brief entry f.([1, 2, 3]) . This is useful to vary the frequency, attenuation parameter, initial coordinate, and initial velocity.

 L = Array{Any}(undef, 3)#     (  ) clr = ["red" "green" "yellow"] function ploter(Answ) for i = 1:3 L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path, Theme(default_color=clr[i]) ) end p = plot(L[1], L[2], L[3]) end Ans1 = garmosc.( [pi 2pi 3pi] )#  p1 = ploter(Ans1) Ans2 = garmosc.( pi, [0.1 0.3 0.5] )#  p2 = ploter(Ans2) Ans3 = garmosc.( pi, 0.1, [0.2 0.5 0.8] ) p3 = ploter(Ans3) Ans4 = garmosc.( pi, 0.1, 0.1, [0.2 0.5 0.8] ) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) ) #     

Now we will consider not small oscillations, but oscillations of arbitrary amplitude:

The graph of the solution on the phase plane is not an ellipse (which indicates the nonlinearity of the oscillator). The less we choose the amplitude of oscillations (i.e., the initial conditions), the less non-linearity will appear (therefore, the small oscillations of the pendulum can be considered harmonic).

 function ungarmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) function syst(du,u,p,t) du[1] = u[2] du[2] = -sin( ω*u[1] )+γ*u[2] end u0 = [x0, y0] # start cond-ns tspan = (0.0, 2pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end Ans1 = ungarmosc.( [pi 2pi 3pi] ) p1 = ploter(Ans1) Ans2 = ungarmosc.( pi, [0.1 0.4 0.7] ) p2 = ploter(Ans2) Ans3 = ungarmosc.( pi, 0.1, [0.1 0.5 0.9] ) p3 = ploter(Ans3) Ans4 = ungarmosc.( pi, 0.1, 0.1, [0.1 0.5 0.9] ) p4 = ploter(Ans4) vstack( hstack(p1,p2), hstack(p3,p4) )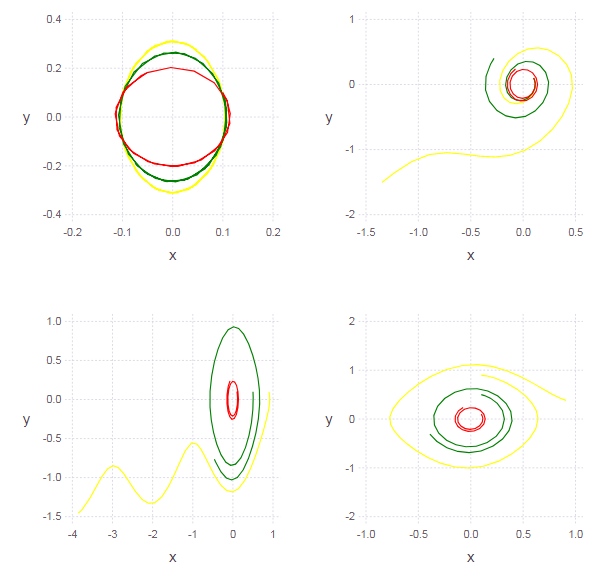 

Brusselator

This model describes some autocatalytic chemical reaction in which diffusion plays a certain role. The model was proposed in 1968 by Lefebvre and Prigogine

Unknown functions $$$u_1 (t), \, u_2 (t)$reflect the dynamics of the concentration of intermediate products of a chemical reaction. Model parameter $$$\ mu$It makes sense to the initial concentration of the catalyst (the third substance).

In more detail, the evolution of the phase portrait of the Brusselator can be observed by performing calculations with a different parameter. $$$\ mu$. When it is increased, the node will first gradually shift to a point with coordinates (1, $$$\ mu$) until it reaches the bifurcation value $$$\ mu$= 2. At this point, there is a qualitative restructuring of the portrait, expressed in the birth of the limiting cycle. With further increase $$$\ mu$there is only a quantitative change in the parameters of this cycle.

 function brusselator(μ = 0.1, u0 = [0.1; 0.1]) function syst(du,u,p,t) du[1] = -(μ+1)*u[1] + u[1]*u[1]*u[2] + 1 du[2] = μ*u[1] - u[1]*u[1]*u[2] end tspan = (0.0, 10) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 1) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end L = Array{Any}(undef, 10) function ploter(Answ) for i = 1:length(Answ) L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path ) end plot(L[1], L[2], L[3], L[4], L[5], L[6], L[7], L[8], L[9], L[10]) end SC = [ [0 0.5], [0 1.5], [2.5 0], [1.5 0], [0.5 1], [1 0], [1 1], [1.5 2], [0.1 0.1], [0.5 0.2] ] Ans1 = brusselator.( 0.1, SC ) Ans2 = brusselator.( 0.8, SC ) Ans3 = brusselator.( 1.6, SC ) Ans4 = brusselator.( 2.5, SC ) p1 = ploter(Ans1) p2 = ploter(Ans2) p3 = ploter(Ans3) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) ) 

It's enough for today. Next time we’ll try to learn how to use another graphic package on new tasks, at the same time getting a hand on Julia’s syntax. In the process of solving problems, one slowly begins to trace not only the pros and cons ... more likely pleasantness and inconvenience — a separate conversation should be devoted to this. And of course, I would like to see something more serious in my games with functions — so I urge the julists to tell more about serious projects, this would help many people and me in particular in learning this wonderful language.