Sly prefix C tree implementation

Introduction

It has been a long four months since the publication of the article about my attempt at a low-level implementation of the prefix tree . Despite all my efforts, the ceiling on which my past implementation of the prefix tree was capable of was ~ 80 thousand words per second. Then I spent a lot of time and effort, but the result would be useful only as a laboratory work on computer science.

Many then told me: “Do not reinvent the wheel, which has already been invented! Use a turnkey solution. ” The difficulty is that I could not use something that I did not understand, even in general outlines.

I seem to understand the prefix tree, and this is what was achieved.

Principle of operation

I do not know English very well, so of the many articles read on the topic of prefix trees, for sure some of the information did not reach me. Therefore, I thought of how to arrange everything, understanding only the basic principle of the prefix tree operation. For those who do not know, I will try to describe it more clearly than it is written in Wikipedia. So I explained what I was doing to my wife.
')
A prefix tree is a logical structure for storing data that can be represented as a card index of books in a library. Each drawer has a number. Each box corresponds to a specific letter of the alphabet. Inside are the numbers of the following boxes, opening which you can find out the following and so on. When inside the box there is nothing, it means that the letter of this box is the last in the word. The problem is that some drawers are almost empty, because they contain 1 or 2 rooms, and the remaining space is empty.

To solve this problem, many varieties of prefix trees appeared, including: HAT-trie, double-array trie, tripple-array trie. Exactly that I could not thoroughly understand the principle of their work pushed me onto a tree as simple as a library file cabinet.

The last time I managed to implement a fairly economical memory consumption implementation of a simple prefix tree. Continuing this metaphor with a library card file, I made boxes in my card file of various sizes, the box is the largest for a complete alphabet, the smallest for 1 letter.

This very PHP scheme I managed to implement in C.

1. Each letter of the word in the installed table is encoded with a number from 2 to 95. For example, the word “abc” is encoded with three numbers: 11, 12, 13. For maximum speed, a two-dimensional array of numbers 1 byte uint8_t abc[256][256] = {}; For conversion, the program reads a string of 1 byte, the value of each byte, it tries to take in our array. For example, the code of the digit 1 = 49, so we look abc[49][0]; . If there is a value other than '\ 0', then this is the code of our letter, remember it and go to the next byte. In our case, the word “abb” consists of a sequence of 6 bytes, two bytes per letter: 208, 176, 208, 177, 208, 178. Since the utf-8 encoding is designed so that the first bytes of single-byte characters never coincide with the first multibyte bytes , in our array abc[208][0] = 0; .

However, for byte pairs there are some coincidences:

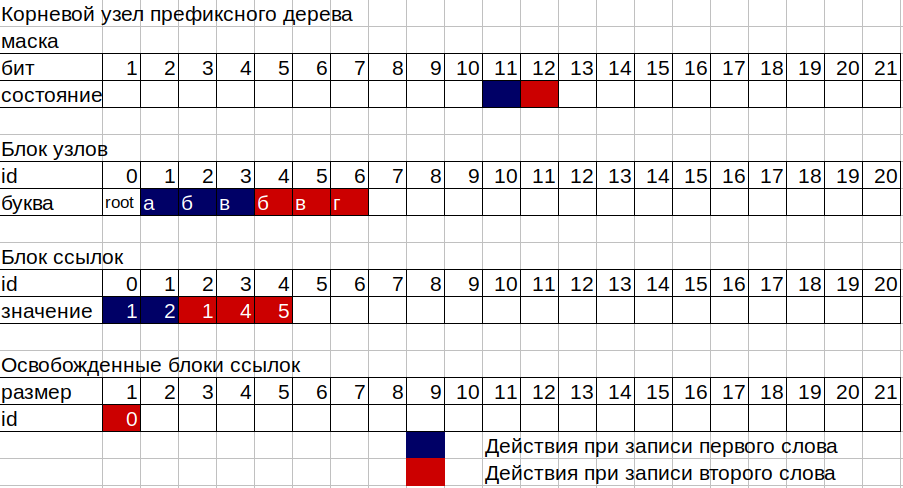
 /*  [11] */ abc[208][176] = 11; /*  [12] */ abc[208][177] = 12; /*  [13] */ abc[208][178] = 13; 

2. Now we need to write the numbers 11, 12 and 13 in the boxes of our tree. The tree consists of 2 separate continuous memory blocks, the first is a block of nodes, the second is a block of links, and also two counters of occupied nodes and occupied cells of a block of links. Each node of the tree consists of 16 bytes, 12 bytes of the bit mask and 4 bytes for storing the id of the link block. The mask allows you to store numbers from 2 to 96 bits. The first bit of the mask is used for the word end flag on this node. Each node can correspond to an id from a block of links if at least one letter is written in this node, or not to correspond if the node is a “leaf” in terms of trees, that is, a word just ends on it. Librarian, empty box.

3. Take the mask of the first (root) node. trie-> nodes [0] .mask; We consider the bits raised in this mask, starting with the second (the first for the word ending flag). If not a single bit in the mask is raised, i.e. the node is empty, then we will need a block of links of size 1 to store our number 11, take the number from the block's link counter and increment the old value by one (after all, we need size 1). We take the number from the node count and also increase the old value by 1. Write the id of the link block to our root node, which is the number obtained from the link block counter. And in this link block id we write the id of the new node, that is, the number obtained from the node count. Now, in addition to the root node (id 0), we have the letter “a” node (id 1). To write the number 12, corresponding to the letter “b”, we do the same, but already with the node letter “a”.

4. On the last letter "in" we do not need a place in the link unit, since we will have the last node in a branch or node - sheet. At such a node only 1 bit in the mask is raised.

5. The most difficult part of the work of the tree occurs when writing occurs in a node in which some letters have already been written. In this case, the scheme of work is as follows:

Suppose we want to add the word “bvg” (12, 13, 14) to our tree, in which the word “abb” (11, 12, 13) is already written. We count the bits in the mask of the root node to the bit of the letter of interest to us. We have the letter “b” with code 12, so the bit of this letter 12, in the mask from 1 to 12 bits, bit 11 is already raised from the letter “a”. So we have the current size of the block of links for the root node 1. We write the second letter, which means we now need a block of links of size 2. Here comes the registry of released blocks, which are written id and size of sections in the block of links that are no longer used by nodes tree. Our old id of the link block for the root node of size 1 is exactly in the register of free sites of size 1, since our root node needs a bigger size. Our registry does not have a suitable area of ​​size 2 and again we take the value from the reference block counter as the new link block id, increasing the counter by 2. At the new address of the link block in the same order in which the bits are located in the node mask, we write the id value node from the old block of references for the letter "a" of the first word and the meaning of the newly created node of the letter "b" of the second word.

Work speed

Drum roll sounds ... Remember the last result? About 80 thousand words per second. The tree was created from the dictionary of all Russian words OpenCorpora 3 039 982 words. But what happened now:

 yatrie creation time: 4.588216s (666k wps) yatrie search time 1 mln. rounds: 0.565618s (1.76m wps) 

UPDATE 11/01/2018:
In version 0.0.2, it was still possible to raise the speed almost 2 times by replacing full-fledged functions with macro functions, as well as changing the structure of the node mask by the uint32_t mask [3], it used to be uint8_t mask [12].
Also added LIKELY () UNLIKELY () macros to predict the expected results in those if () blocks, where possible.
UPDATE 11/05/2018:
Twisted a little more. It was possible to make it work normally even when compiling -O3 and -Ofast. The search speed in the tree is ~ 0.2 μs or 0.2c per 1 million repetitions. Apparently this speed was obtained thanks to the transition to a different mask format. There used to be 12 bytes of 8 bits, and now there are 3 int32 and a very fast function of counting bits in int32.

How compact is all this?

The specified OpenCorpora dictionary occupies ~ 84MB, which is not much worse than libdatrie, which gives ~ 80MB.

→ Source Code

Welcome!