How to make even more incorrect states even more inexpressible

Not so long ago on Habré translated an article about how using algebraic data types to ensure that incorrect states were ineffable. Today we will look at a slightly more generalized, scalable and secure way to express the inexpressible, and haskel will help us in this.

In short, in this article some entity is considered with a postal address and an e-mail address, as well as with an additional condition that there must be at least one of these addresses. How is it proposed to express this condition at the type level? It is proposed to record addresses as follows:

type ContactInfo = | EmailOnly of EmailContactInfo | PostOnly of PostalContactInfo | EmailAndPost of EmailContactInfo * PostalContactInfo 

What are the problems with this approach?

The most obvious (and it was noted several times in the comments to that article) - this approach is not scalable at all. Imagine that we have not two types of addresses, but three or five, and the condition of correctness looks like “there must be either a postal address or an email address and an office address at the same time, and there should not be several addresses of the same type”. Anyone can write the appropriate type as an exercise for self-checking. The task with an asterisk is to rewrite this type for the case when the condition about the absence of duplicates disappeared from the TZ.

We divide

How can this problem be solved? Let's try to fantasize. Only first we will decompose and divide the address class (for example, mail / email / table number in the office) and the contents corresponding to this class:

 data AddrType = Post | Email | Office 

We will not think about the content yet, because there is nothing about it in the statement of work on the condition of the validity of the address list.

If we checked the corresponding condition in the runtime of some constructor of some ordinary OOP-language, then we would just write a function like

 valid :: [AddrType] -> Bool valid xs = let hasNoDups = nub xs == xs --      hasPost = Post `elem` xs hasEmail = Email `elem` xs hasOffice = Office `elem` xs in hasNoDups && (hasPost || (hasEmail && hasOffice)) 

And would throw any, if it returns False .

Can we instead check for a similar condition using a tip checker when compiling? It turns out that yes, we can, if the type system of the language is sufficiently expressive, and the rest of the article we will pick this approach.

Here dependent types will help us a lot, and since the most adequate way to write seized code on a Haskel is to first write it on aqda or Idris, we will sharply change our shoes and we will write on Idris. Idris syntax is close enough to a Haskel: for example, the above function only needs to change the signature a little:

 valid : List AddrType -> Bool 

Now remember that in addition to the address classes, we also need their contents, and encode the dependence of the fields on the address class as GADT:

 data AddrFields : AddrType -> Type where PostFields : (city : String) -> (street : String) -> AddrFields Post EmailFields : (email : String) -> AddrFields Email OfficeFields : (floor : Int) -> (desk : Nat) -> AddrFields Office 

That is, if we are given a value of fields type AddrFields t , then we know that t is some class of AddrType , and that in fields lies a set of fields corresponding to this particular class.

 addrFields : AddrType -> Type addrFields Post = PostFields addrFields Email = EmailFields addrFields Office = OfficeFields 

What is the entire address in this model? This is a pair from the address class and the corresponding fields:

 Addr : Type Addr = (t : AddrType ** AddrFields t) 

Fans of type theory will say that this is an existential dependent type: if we are given some value of type Addr , then this means that there is a value t type AddrType and a corresponding set of fields AddrFields t . Naturally, the addresses of different classes are of the same type:

 someEmailAddr : Addr someEmailAddr = (Email ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (Office ** OfficeFields (-2) 762) 

Moreover, if we are given EmailFields fields, then the only address class that matches is Email , so you can leave it out, the type checker will display it himself:

 someEmailAddr : Addr someEmailAddr = (_ ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (_ ** OfficeFields (-2) 762) 

Let us write an auxiliary function, which according to the list of addresses gives the corresponding list of classes of addresses, and immediately generalize it before working on an arbitrary functor:

 types : Functor f => f Addr -> f AddrType types = map fst 

Here the existential type Addr behaves like a familiar couple: in particular, you can ask for its first component AddrType (task with an asterisk: why ask the second component so it does not work out?).

Raise

Now we come to the key part of our story. So, we have a List Addr address list and some valid : List AddrType -> Bool predicate valid : List AddrType -> Bool , the execution of which for this list we want to guarantee at the level of types. How can we combine them? Of course, another type!

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst 

Now we will understand what we have written here.

data ValidatedAddrList : List Addr -> Type where means that the type ValidatedAddrList parameterized by the address list itself.

Let's look at the signature of the only MkValidatedAddrList constructor of this type: (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst . That is, it takes some list of addresses lst and one more argument prf type valid (types lst) = True . What does this type mean? It means that the value to the left of = is equal to the value to the right of = , that is, valid (types lst) is actually True.

How it works? The signature = looks like (x : A) -> (y : B) -> Type . That is, = takes two arbitrary values ​​of x and y (perhaps even different types of A and B , which means that the inequality in Idris is heterogeneous, and that is somewhat ambiguous from the point of view of type theory, but this is a topic for a separate discussion). Due to what then equality is demonstrated? And due to the fact that the only constructor = - Refl with a signature of almost (x : A) -> x = x . That is, if we have a value of type x = y , then we know that it was built using Refl (because there are no other constructors), which means that x is actually equal to y .

Note that this is why, at best, we will always pretend at best that we are proving something, because there is undefined in Haskel, which populates any type, so the above reasoning does not work there: for any x , y term is type x = y could be created via undefined (or through infinite recursion, let's say that by and large the same thing from the point of view of type theory).

We also note that equality here is not in the sense of Haskell's Eq or some kind of operator== in C ++, but significantly more rigorous: structural, which, simplifying, means that two values ​​have the same form . That is, to deceive him so simply will not work. But equality issues are traditionally pulled into a separate article.

In order to consolidate our understanding of equality, we write unit tests on the valid function:

 testPostValid : valid [Post] = True testPostValid = Refl testEmptyInvalid : valid [] = False testEmptyInvalid = Refl testDupsInvalid : valid [Post, Post] = False testDupsInvalid = Refl testPostEmailValid : valid [Post, Email] = True testPostEmailValid = Refl 

These tests are good because you don’t even need to run them; it’s enough that the TIP checker checked them. Indeed, let's replace True with False , for example, in the very first of them and see what happens:

 testPostValid : valid [Post] = False testPostValid = Refl 

Typcheker cuss

as expected. Wonderful.

Simplified

Now let's review our ValidatedAddrList bit.

First, the pattern of comparing some value with True quite common, so there is a special type So for this: you can take So x as a synonym for x = True . Let's fix the definition of ValidatedAddrList :

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : So (valid $ types lst)) -> ValidatedAddrList lst 

In addition, there is a convenient auxiliary function for choose for So , which in its sense raises a check for the level of types:

 > :doc choose Data.So.choose : (b : Bool) -> Either (So b) (So (not b)) Perform a case analysis on a Boolean, providing clients with a So proof 

We need it when we write functions that modify this type.

Secondly, sometimes (especially with interactive development), the idris can find a suitable prf value prf its own. In order in such cases it was not necessary to design it by hand, there is an appropriate syntactic sugar:

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> {auto prf : So (valid $ types lst)} -> ValidatedAddrList lst 

Curly brackets mean that this is an implicit argument that idris will try to pull out of context, and auto means that he will also try to construct it himself.

So, what does this new ValidatedAddrList give us? And it gives this chain of reasoning: let val be a value of type ValidatedAddrList lst . This means that lst is some address list, and besides, val was created using the MkValidatedAddrList constructor, to which we passed this same lst and another prf value of type So (valid $ types lst) , which is almost valid (types lst) = True . And in order for us to build prf , we need, in fact, to prove that this equality holds.

And the most beautiful thing is that everything is checked by the tickpicker. Yes, validation will have to be performed at runtime (because addresses can be read from a file or from a network), but the type checker guarantees that this check will be done: without it, ValidatedAddrList cannot be created. At least in Idris. In Haskel it is possible, alas.

We insert

To make sure that verification is inevitable, we will try to write a function to add an address to the list. First try:

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = MkValidatedAddrList (addr :: lst) 

Nope, the typchecker gives on the fingers (although not very readable, the cost of valid too complicated):

How do we get a copy of this here So ? No other than the above choose . Second attempt:

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => MkValidatedAddrList (addr :: lst) Right r => ?rhs 

It is almost secret check. “Almost” because it is not clear what to substitute for rhs . Rather, it is clear: in this case, the function must somehow report the error. So, we need to change the signature and wrap the return value, for example, in Maybe :

 insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Just $ MkValidatedAddrList (addr :: lst) Right r => Nothing 

This is tipped and works as it should.

But now the following is not a very obvious problem, which was, in fact, in the original article. The type of this function does not interfere with writing such an implementation:

 insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = Nothing 

That is, we always say that we could not build a new address list. Tips? Yes. Correctly? Well, hardly. Can this be avoided?

It turns out that it is possible, and we have all the necessary tools for this. In case of success, insert returns ValidatedAddrList , which contains evidence of this very success. So add elegant symmetry and ask the function to return more and proof of failure!

 insert : (addr : Addr) -> ValidatedAddrList lst -> Either (So (not $ valid $ types (addr :: lst))) (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Right $ MkValidatedAddrList (addr :: lst) Right r => Left r 

Now we can not just take and always return Nothing .

Similarly, you can do for address removal functions and the like.

Let's see how it all looks in the end now.

Let's try to create an empty address list:

It is impossible, the empty list is not valid.

How about a list of just one email address?

OK, let's try to insert the postal address into the list, in which there is already an postal address:

Let's try to insert an email:

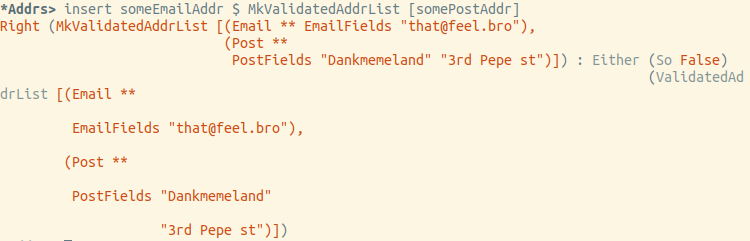
In the end, everything works exactly as expected.

Ffuh. I thought it would be three lines, but it worked a little longer. So explore how far we can go to Haskel, we will be in the next article. In the meantime, a little

Ponder

What is the result of the profit of such a decision in comparison with the one given in the article to which we referred at the very beginning?

1. It is, again, much more scalable. Complex validation functions are easier to write.
2. It is more isolated. The client code is generally not obliged to know what is inside the validation function, whereas the ContactInfo form from the original article requires you to tie it up.
3. The logic of validation is written in the form of ordinary and familiar functions, so that you can immediately check it with thoughtful reading and test with time-tests, and not deduce the meaning of the test from the form of the data type representing the already verified result.
4. It becomes possible to slightly more accurately specify the behavior of functions that work with the type of data that we are interested in, especially in the case of failure to check. For example, the insert written as a result cannot simply be written incorrectly . Similarly, one could write insertOrReplace , insertOrIgnore and the like, whose behavior is fully specified in the type.

What is the profit compared to the OOP solution in this spirit?

 class ValidatedAddrListClass { public: ValidatedAddrListClass(std::vector<Addr> addrs) { if (!valid(addrs)) throw ValidationError {}; } }; 

1. The code is more modularized and secure. In the case of the above, verification is an action that is checked once and which was later forgotten. Everything rests on the word of honor and agreement that if you have a ValidatedAddrListClass , then its implementation once there made a check. The very fact of this check from the class as some value can not be picked out. In the case of values ​​of some type, this value can be transferred between different parts of the program, used to build more complex values ​​(for example, again, negating this test), explore (see the next paragraph) and generally do the same thing that we used to do. with values.
2. Such checks can be used with (dependent) pattern matching. True, not in the case of this valid function and not in the case of Idris, it is painfully complicated, and Idris is painfully stupid so that information useful for patterns can be extracted from the valid structure. Nevertheless, valid can be rewritten in a slightly more pattern-friendly style, but this is beyond the scope of this article and is generally nontrivial in itself.

What are the disadvantages?

I see only one serious fundamental flaw: valid is too stupid a function. It returns only one bit of information - validated or not. In the case of smarter types, we could achieve something more interesting.

For example, imagine that the requirement of unique addresses is missing from the TK. In this case, it is obvious that adding a new address to an existing list of addresses will not make the list invalid, so one could prove this theorem by writing a function of type So (valid $ types lst) -> So (valid $ types $ addr :: lst) , and use it, for example, to write a type-safe always successful

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) 

But, alas, theorems like recursion and induction, and in our problem there is no elegant inductive structure, therefore, in my opinion, the code with valid oak boolean is also not bad.