Hi, the community of developers , it is necessary to finish business.

In my previous opus, there was a call to show how the Prolog language can be used, and to show that it would be fun. Turn this into an exercise.

I will try to continue show off to demonstrate.

Briefly recall the task:

Prove the completeness of the solution failed. On the site that provides the task there are 1808 tests that cannot be immediately seen, you need to write a program and get another test as an error.

Hardcore I got 66 from him and checked my solution - while everything worked. But it can not be so simple.

Why do so many tests, I want to check further ...

I will try to rewrite this solution in language understandable available on this system (they reflect the popularity of modern programming languages).

So, choose Python.

The power of Prolog in the search procedure, the roots of which are in the methods of proving theorems . Simply put, it has a built-in mechanism for unification and search with a return. It is even simpler to say mapping plus depth search in a decision tree.

And Python is a modern Pascal (something already three languages ​​on the letter "P")), it is also possible to write programs on it for schoolchildren .

Now I will rewrite the solution that was laid in the previous implementation and quickly implement a similar prolog search with a return.

Then I will launch it into the testing system, and I will see if the move (code) was correct.

Join now.

At the entrance, the test string and pattern:

def test(st,pat): if st=="" and pat=="": yield True if pat>"" and pat[0]=='*':yield test(st,pat[1:]) if st>"" and pat>"": if st[0]==pat[0] or pat[0]=='?': yield test(st[1:],pat[1:]) if pat[0]=='*':yield test(st[1:],pat) yield False 

It seems to be very similar to the implementation of Prolog:

 test_pattrn([],[]). test_pattrn([Ch|UnpTail],[Ch|PatTail]):-test_pattrn(UnpTail,PatTail). test_pattrn([Ch|UnpTail],['?'|PatTail]):-test_pattrn(UnpTail,PatTail). test_pattrn([Ch|UnpTail],['*'|PatTail]):-test_pattrn(UnpTail,['*'|PatTail]). test_pattrn(Str,['*'|PatTail]):-test_pattrn(Str,PatTail). 

Five solutions, otherwise a lie.

But how to do a return search ?, for this I use yield, as it is called there, unfinished (lazy) calculations, closure, an element of the functional approach, tell me ... It will return something from which you can get the following solution, but if will not lead to the correct answer, then we will go to the program branch with the next yield, this is the difference from return.

This function will accept the result of the first test () as an input, if it is true then everything is fine, otherwise it will try to iterate more, and so will be a depth search similar to the prolog output.

Here, return is already specifically needed:

 def run(r): if type(r)==bool: if r==True: return True else: for nr in r: if run(nr):return True return False 

Checking 1

Wow, this is the result, "939/1808 test cases passed." and "Status: Time Limit Exceeded".
This is exactly what I expected; a declarative solution does not always lead to an effective implementation time. Transparent wording is not a quick wording.

But, here is the result of the python, let's test the opened test in the implementation from the first article, and measure the time:

 import time pt=time.time() print(run(test("babaaababaabababbbbbbaabaabbabababbaababbaaabbbaaab","***bba**a*bbba**aab**b"))) print(time.time()-pt) 

Runtime by Python 11.10963249206543 sec., Yes, a bit too much.

Improved testing mechanism for Prolog:

 %unit-tests framework assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is Fin-St,writeln(Goal->ok:Per/sec). assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is Fin-St,writeln(Goal->ok:Per/sec). assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp). :-assert_are_equal(isMatch(aaabababaaabaababbbaaaabbbbbbabbbbabbbabbaabbababab,'*ab***ba**b*b*aaab*b'),true). 

And here is the result of Prolog (running not in the online editor, locally, on the same hardware as the previous one):

 isMatch(aaabababaaabaababbbaaaabbbbbbabbbbabbbabbaabbababab,*ab***ba**b*b*aaab*b)->ok:2.208951950073242/sec 

It looks like I do not use python badly ((, it is necessary to improve, not so visually:

 def test(st,pat): if st==pat: return True if pat>"" and pat[0]=='*': if test(st,pat[1:]):return True if st>"" and pat>"": if st[0]==pat[0] or pat[0]=='?': if test(st[1:],pat[1:]):return True if pat[0]=='*': if test(st[1:],pat):return True return False import time pt=time.time() print(test("babaaababaabababbbbbbaabaabbabababbaababbaaabbbaaab","***bba**a*bbba**aab**b")) print(time.time()-pt) 

Here is the result: 3.921879768371582 sec. (this is closer to the original). We return to the arbitrator:

Once again.

I conclude that the total passing of tests goes beyond the time frame, because the last two options are solved very quickly.

Need optimization on the order.

Check 2. Need optimization.

What begs, for sure - search in width.

Do not continue the decision of each branch until we get a lie and return to another branch, but look through the solutions by levels, descending simultaneously for each option and gradually go deeper further.

I'll try to make it a python, and then I'll demonstrate the prologue.

 def test(st,pat): if st==pat: return True res=[] #     ,    if pat>"" and pat[0]=='*':res+=[(st,pat[1:])] if st>"" and pat>"": stt=st[1:] if st[0]==pat[0] or pat[0]=='?':res+=[(stt,pat[1:])] if pat[0]=='*':res+=[(stt,pat)] return res def run(st,pat): lev=[(st,pat)] while len(lev)!=0: nxt=set() ##        for s,p in lev: one=test(s,p) if one==True:return True else:nxt.update(set(one)) lev=nxt return False 

There is already a result for test 939, only 0.01585698127746582 seconds.
and ..., URA this decision is made

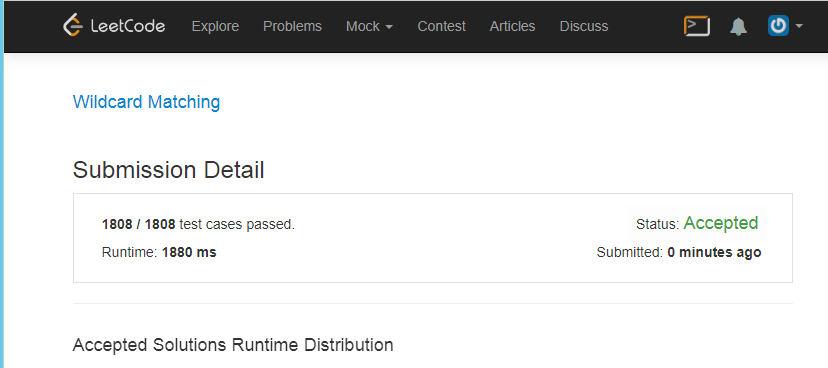
Prologue

I will try to show how to implement a search in width, in a declarative implementation. To do this, there are special predicates of the second order, which can assemble solutions into the list, for example, bagof, setof, findall.

bagof (+ Template,: Goal, -Bag)
Unify Bag with the alternatives of Template. The bagof / 3 will be able to track your bag. Not in the bind Var in Goal. bagof / 3 fails if goal has no solutions.
setof (+ Template, + Goal, -Set)
This is a list of alternatives without duplicates.

The predicate setof works well. he already knows how to remove duplicates (in the python for this I had to learn about sets).

So, I will make a predicate that gets a solution of one level, then we collect it with another predicate and delve into it, here’s the complete solution:

 atom_to_list(Str,[Ch|T]) :- atom_concat(Ch,Rest,Str),atom_length(Ch,1), atom_to_list(Rest,T). %  pattrn(X:X,true). %-      pattrn([Ch|UnpTail]:[Ch|PatTail],UnpTail:PatTail). pattrn([_|UnpTail]:['?'|PatTail],UnpTail:PatTail). pattrn([_|UnpTail]:['*'|PatTail],UnpTail:['*'|PatTail]). pattrn(Str:['*'|PatTail],Str:PatTail). %  true,     ,     next_level(Lev):-member(true,Lev),!. next_level(Lev):-setof(One,SP^(member(SP,Lev),pattrn(SP,One)),Next),!, next_level(Next). test_pattrn(Str,Pat):-next_level([Str:Pat]). isMatch(S,P) :- atom_to_list(S,SL), atom_to_list(P,PL),!, test_pattrn(SL,PL),!. %unit-tests framework assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is Fin-St, writeln(Goal->ok:Per/sec). assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is Fin-St, writeln(Goal->ok:Per/sec). assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp). %all test :-assert_are_equal(isMatch(aa,a),false). :-assert_are_equal(isMatch(aa,'*'),true). :-assert_are_equal(isMatch(cb,'?a'),false). :-assert_are_equal(isMatch(adceb,'*a*b'),true). :-assert_are_equal(isMatch(acdcb,'a*c?b'),false). :-assert_are_equal(isMatch(aab,'c*a*b'),false). :-assert_are_equal(isMatch(mississippi,'m??*ss*?i*pi'),false). :-assert_are_equal(isMatch(abefcdgiescdfimde,'ab*cd?i*de'),true). :-assert_are_equal(isMatch(zacabz,'*a?b*'),false). :-assert_are_equal(isMatch(leetcode,'*e*t?d*'),false). :-assert_are_equal(isMatch(aaaa,'***a'),true). :-assert_are_equal(isMatch(b,'*?*?*'),false). :-assert_are_equal(isMatch(aaabababaaabaababbbaaaabbbbbbabbbbabbbabbaabbababab,'*ab***ba**b*b*aaab*b'),true). :-assert_are_equal(isMatch(abbbbbbbaabbabaabaa,'*****a*ab'),false). :-assert_are_equal(isMatch(aaabababaaabaababbbaaaabbbbbbabbbbabbbabbaabbababab,'*ab***ba**b*b*aaab*b'),true). :-assert_are_equal(isMatch(babaaababaabababbbbbbaabaabbabababbaababbaaabbbaaab,'***bba**a*bbba**aab**b'),false). 

Here you can see that the rule that previously performed a pattern-based search, as if making a transition along a face in a graph, has now become a set of pattrn facts that contain possible transitions (connections between states) - this is a description of the graph, and not its implementing code.

And results of performance with time in sec .:

 isMatch(aa, a)->ok:0.00010013580322265625/sec isMatch(aa, *)->ok:4.00543212890625e-5/sec isMatch(cb, ?a)->ok:3.981590270996094e-5/sec isMatch(adceb, *a*b)->ok:0.0001399517059326172/sec isMatch(acdcb, a*c?b)->ok:9.989738464355469e-5/sec isMatch(aab, c*a*b)->ok:4.00543212890625e-5/sec isMatch(mississippi, m??*ss*?i*pi)->ok:0.0003399848937988281/sec isMatch(abefcdgiescdfimde, ab*cd?i*de)->ok:0.0003600120544433594/sec isMatch(zacabz, *a?b*)->ok:9.989738464355469e-5/sec isMatch(leetcode, *e*t?d*)->ok:0.00020003318786621094/sec isMatch(aaaa, ***a)->ok:9.989738464355469e-5/sec isMatch(b, *?*?*)->ok:6.008148193359375e-5/sec isMatch(aaabababaaabaababbbaaaabbbbbbabbbbabbbabbaabbababab, *ab***ba**b*b*aaab*b)->ok:0.0040400028228759766/sec isMatch(abbbbbbbaabbabaabaa, *****a*ab)->ok:0.0006201267242431641/sec isMatch(aaabababaaabaababbbaaaabbbbbbabbbbabbbabbaabbababab, *ab***ba**b*b*aaab*b)->ok:0.003679990768432617/sec isMatch(babaaababaabababbbbbbaabaabbabababbaababbaaabbbaaab, ***bba**a*bbba**aab**b)->ok:0.002460002899169922/sec 

And this is a successful solution not only logically but also in time.

findings

In the previous article, I wanted to see an interest in the topic of a declarative approach. The theme "niasilil such an approach" immediately opened, yet you can show interest. Here I showed that there is a performance problem, what is written clearly does not work quickly. Attempts to create a parallel prologue did not end with success. Maybe there is a question of the future, can a quantum computer ??
Total use puzzles on the above site, for a pleasant stay with the mind.

Well, next time there will be an attempt to immediately solve another one of the hard tasks effectively.