The implementation of the algorithm k-means (k-average) on the example of working with pixels
Hello! Recently, it was necessary to write code to implement image segmentation using the k-means method. Well, google first thing to help. I found a lot of information, as well as from a mathematical point of view (all sorts of complex mathematical scribbles there, you will understand what the fuck is written there), and some software implementations that exist on the English Internet. Of course, these codes are beautiful - no doubt, but the very essence of the idea is hard to catch. Somehow it’s all complicated there, confusing, and as long as you don’t write the code with your hands, you don’t understand anything. In this article I want to show a simple, not productive, but, I hope, understandable implementation of this wonderful algorithm. Okay, drove!
So what is clustering in terms of our perception? I will give an example, for example, there is a cute image with flowers from your grandmother’s dacha.

The question is: to determine how many areas of this photo are filled with approximately one color. Well, it’s not at all difficult: white petals - once, yellow centers - two (I am not a biologist, as they are called, I don’t know), greenery - three. These areas are called clusters. Cluster - combining data with common characteristics (color, position, etc.). The process of determining and placing each component of any data in such clusters - areas is called clustering.
')
There are many clustering algorithms, but the simplest of them is k-means, which will be discussed further. K-means is a simple and efficient algorithm that is easy to implement using a software method. The data that we will distribute across clusters is pixels. As you know, a color pixel has three components - red, green and blue. The overlay of these components creates a palette of existing colors.
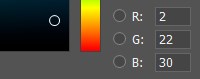
In the computer's memory, each component of a color is characterized by a number from 0 to 255. That is, by combining different values of red, green and blue, we get a color palette on the screen.
On the example of pixels, we implement our algorithm. K-means is an iterative algorithm, that is, it will give the correct result, after a certain number of repetitions of some mathematical calculations.
I will implement this project in C ++. The first file is “k_means.h”, in it I defined the main data types, constants, and the main class for work is “K_means”.
To characterize each pixel, we will create a structure that consists of three pixel components, for which I chose the double type for more accurate calculations, and also defined some constants for the program to work:
The K_means class itself:
Let's run through the class components:
vectorpixcel - vector for pixels;
q_klaster - the number of clusters;
k_pixcel - the number of pixels;
vectorcentr - vector for clustering centers, the number of elements in it is determined by q_klaster;
identify_centers () is a method for randomly selecting initial centers among input pixels;
compute () and compute_s () built-in methods for calculating the distance between pixels and recalculating centers, respectively;
three constructors: the first by default, the second for initializing pixels from an array, the third for initializing pixels from a text file (in my implementation, first the file is randomly filled with data, and then pixels are read from this file for the program to work, why not directly into a vector just need in my case);
clustering (std :: ostream & os) - clustering method;
method and operator output overload for publishing results.
Implementation methods:
This is a method for selecting initial clustering centers and adding them to the centers vector. A check is made on the repetition of centers and their replacement in these cases.
Implement a constructor to initialize pixels from an array.
In this constructor, we pass an input object for the ability to enter data from both the file and the console.
The output of the initial data.
This example is planned in advance, the pixels are selected specifically for demonstration. The program needs two iterations to group the data into three clusters. Looking at the centers of the last two iterations, you can see that they almost stayed in place.
More interesting cases with random pixel generation. Having generated 50 points that need to be divided into 10 clusters, I got 5 iterations. Having generated 50 points that need to be divided into 3 clusters, I got all 100 maximum allowed iterations. You can see that the more clusters, the easier it is for the program to find the most similar pixels and combine them into smaller groups, and vice versa - if there are few clusters and many points, the algorithm often ends only by exceeding the maximum allowed number of iterations, since some pixels constantly jump from one cluster to another. Nevertheless, the bulk is still defined in their clusters finally.
Well, now let's check the result of clustering. Taking the result of some clusters from the example of 50 points on 10 clusters, I hammered the result of this data into Illustrator and this is what happened:
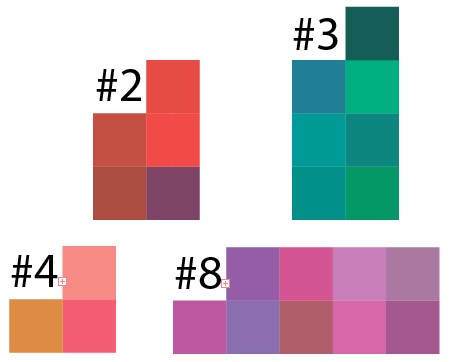
It can be seen that in each cluster any shades of color prevail, and here you need to understand that the pixels were chosen randomly; an analogue of such an image in real life is some kind of picture that was randomly sprinkled with all colors and it is difficult to isolate areas of similar colors.
Suppose we have such a photo. We can define an island as one cluster, but with an increase we see that it consists of different shades of green.

And this is the 8th cluster, but in a smaller version, the result is similar:

The full version of the program can be viewed on my GitHub .
So what is clustering in terms of our perception? I will give an example, for example, there is a cute image with flowers from your grandmother’s dacha.

The question is: to determine how many areas of this photo are filled with approximately one color. Well, it’s not at all difficult: white petals - once, yellow centers - two (I am not a biologist, as they are called, I don’t know), greenery - three. These areas are called clusters. Cluster - combining data with common characteristics (color, position, etc.). The process of determining and placing each component of any data in such clusters - areas is called clustering.
')
There are many clustering algorithms, but the simplest of them is k-means, which will be discussed further. K-means is a simple and efficient algorithm that is easy to implement using a software method. The data that we will distribute across clusters is pixels. As you know, a color pixel has three components - red, green and blue. The overlay of these components creates a palette of existing colors.

In the computer's memory, each component of a color is characterized by a number from 0 to 255. That is, by combining different values of red, green and blue, we get a color palette on the screen.
On the example of pixels, we implement our algorithm. K-means is an iterative algorithm, that is, it will give the correct result, after a certain number of repetitions of some mathematical calculations.
Algorithm
- You need to know in advance how many clusters you need to distribute the data. This is a significant disadvantage of this method, but this problem is solved by improved implementations of the algorithm, but this is said to be a completely different story.
- We need to choose the initial centers of our clusters. How? Yes, at random. What for? To be able to bind each pixel to the center of the cluster. The center is like a King, around which his subjects are gathered - pixels. It is the “distance” from the center to the pixel that determines who will obey each pixel.
- Calculate the distance from each center to each pixel. This distance is considered as the Euclidean distance between points in space, and in our case - as the distance between the three color components:
$$ display $$ \ sqrt {(R_ {2} -R_ {1}) ^ 2 + (G_ {2} -G_ {1}) ^ 2 + (B_ {2} -B_ {1}) ^ 2} . $$ display $$
We count the distance from the first pixel to each center and determine the smallest distance between this pixel and the centers. For the center, the distance to which is the smallest, recalculate the coordinates, as the arithmetic average between each component of the pixel - the king and the pixel - the subject. Our center is shifted in space, according to calculations. - After recalculating all the centers, we distribute the pixels into clusters, comparing the distance from each pixel to the centers. A pixel is placed in a cluster, to the center of which it is located closer than to the other centers.
- It all starts over again, as long as the pixels remain in the same clusters. Often this may not happen, since with a large amount of data the centers will move in a small radius, and the pixels on the edges of the clusters will jump to one or another cluster. To do this, determine the maximum number of iterations.
Implementation
I will implement this project in C ++. The first file is “k_means.h”, in it I defined the main data types, constants, and the main class for work is “K_means”.
To characterize each pixel, we will create a structure that consists of three pixel components, for which I chose the double type for more accurate calculations, and also defined some constants for the program to work:
const int KK = 10; // const int max_iterations = 100; // typedef struct { double r; double g; double b; } rgb; The K_means class itself:
class K_means { private: std::vector<rgb> pixcel; int q_klaster; int k_pixcel; std::vector<rgb> centr; void identify_centers(); inline double compute(rgb k1, rgb k2) { return sqrt(pow((k1.r - k2.r),2) + pow((k1.g - k2.g), 2) + pow((k1.b - k2.b), 2)); } inline double compute_s(double a, double b) { return (a + b) / 2; }; public: K_means() : q_klaster(0), k_pixcel(0) {}; K_means(int n, rgb *mas, int n_klaster); K_means(int n_klaster, std::istream & os); void clustering(std::ostream & os); void print()const; ~K_means(); friend std::ostream & operator<<(std::ostream & os, const K_means & k); }; Let's run through the class components:
vectorpixcel - vector for pixels;
q_klaster - the number of clusters;
k_pixcel - the number of pixels;
vectorcentr - vector for clustering centers, the number of elements in it is determined by q_klaster;
identify_centers () is a method for randomly selecting initial centers among input pixels;
compute () and compute_s () built-in methods for calculating the distance between pixels and recalculating centers, respectively;
three constructors: the first by default, the second for initializing pixels from an array, the third for initializing pixels from a text file (in my implementation, first the file is randomly filled with data, and then pixels are read from this file for the program to work, why not directly into a vector just need in my case);
clustering (std :: ostream & os) - clustering method;
method and operator output overload for publishing results.
Implementation methods:
void K_means::identify_centers() { srand((unsigned)time(NULL)); rgb temp; rgb *mas = new rgb[q_klaster]; for (int i = 0; i < q_klaster; i++) { temp = pixcel[0 + rand() % k_pixcel]; for (int j = i; j < q_klaster; j++) { if (temp.r != mas[j].r && temp.g != mas[j].g && temp.b != mas[j].b) { mas[j] = temp; } else { i--; break; } } } for (int i = 0; i < q_klaster; i++) { centr.push_back(mas[i]); } delete []mas; } This is a method for selecting initial clustering centers and adding them to the centers vector. A check is made on the repetition of centers and their replacement in these cases.
K_means::K_means(int n, rgb * mas, int n_klaster) { for (int i = 0; i < n; i++) { pixcel.push_back(*(mas + i)); } q_klaster = n_klaster; k_pixcel = n; identify_centers(); } Implement a constructor to initialize pixels from an array.
K_means::K_means(int n_klaster, std::istream & os) : q_klaster(n_klaster) { rgb temp; while (os >> temp.r && os >> temp.g && os >> temp.b) { pixcel.push_back(temp); } k_pixcel = pixcel.size(); identify_centers(); } In this constructor, we pass an input object for the ability to enter data from both the file and the console.
void K_means::clustering(std::ostream & os) { os << "\n\n :" << std::endl; /* : , - , , , .*/ std::vector<int> check_1(k_pixcel, -1); std::vector<int> check_2(k_pixcel, -2); int iter = 0; /* .*/ while(true) { os << "\n\n---------------- №" << iter << " ----------------\n\n"; { for (int j = 0; j < k_pixcel; j++) { double *mas = new double[q_klaster]; /* : . , .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[j], centr[i]); os << " " << j << " #" << i << ": " << *(mas + i) << std::endl; } /* m_k .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } os << " #" << m_k << std::endl; os << " #" << m_k << ": "; centr[m_k].r = compute_s(pixcel[j].r, centr[m_k].r); centr[m_k].g = compute_s(pixcel[j].g, centr[m_k].g); centr[m_k].b = compute_s(pixcel[j].b, centr[m_k].b); os << centr[m_k].r << " " << centr[m_k].g << " " << centr[m_k].b << std::endl; delete[] mas; } /* .*/ int *mass = new int[k_pixcel]; os << "\n : "<< std::endl; for (int k = 0; k < k_pixcel; k++) { double *mas = new double[q_klaster]; /* .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[k], centr[i]); os << " №" << k << " #" << i << ": " << *(mas + i) << std::endl; } /* .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } mass[k] = m_k; os << " №" << k << " #" << m_k << std::endl; } /* .*/ os << "\n : \n"; for (int i = 0; i < k_pixcel; i++) { os << mass[i] << " "; check_1[i] = *(mass + i); } os << std::endl << std::endl; os << " : " << std::endl; int itr = KK + 1; for (int i = 0; i < q_klaster; i++) { os << " #" << i << std::endl; for (int j = 0; j < k_pixcel; j++) { if (mass[j] == i) { os << pixcel[j].r << " " << pixcel[j].g << " " << pixcel[j].b << std::endl; mass[j] = ++itr; } } } delete[] mass; /* .*/ os << " : \n" ; for (int i = 0; i < q_klaster; i++) { os << centr[i].r << " " << centr[i].g << " " << centr[i].b << " - #" << i << std::endl; } } /* – .*/ iter++; if (check_1 == check_2 || iter >= max_iterations) { break; } check_2 = check_1; } os << "\n\n ." << std::endl; } The main clustering method. std::ostream & operator<<(std::ostream & os, const K_means & k) { os << " : " << std::endl; for (int i = 0; i < k.k_pixcel; i++) { os << k.pixcel[i].r << " " << k.pixcel[i].g << " " << k.pixcel[i].b << " - №" << i << std::endl; } os << std::endl << " : " << std::endl; for (int i = 0; i < k.q_klaster; i++) { os << k.centr[i].r << " " << k.centr[i].g << " " << k.centr[i].b << " - #" << i << std::endl; } os << "\n : " << k.q_klaster << std::endl; os << " : " << k.k_pixcel << std::endl; return os; } The output of the initial data.
Sample output
Sample output
Initial pixels:
255 140 50 - №0
100 70 1 - №1
150 20 200 - №2
251 141 51 - № 3
104 69 3 - №4
153 22 210 - №5
252 138 54 - № 6
101 74 4 - №7
Random initial clustering centers:
150 20 200 - # 0
104 69 3 - # 1
100 70 1 - # 2
Number of clusters: 3
Number of pixels: 8
Start of clustering:
Iteration # 0
Distance from pixel 0 to center # 0: 218.918
Distance from pixel 0 to center # 1: 173.352
Pixel Distance 0 to Center # 2: 176.992
Minimum distance to center # 1
We recount the center # 1: 179.5 104.5 26.5
Distance from pixel 1 to center # 0: 211.189
The distance from pixel 1 to the center # 1: 90.3369
Distance from pixel 1 to center # 2: 0
Minimum distance to center # 2
We recount the center # 2: 100 70 1
Distance from pixel 2 to the center # 0: 0
Distance from pixel 2 to the center # 1: 195.225
Distance from pixel 2 to the center # 2: 211.189
Minimum distance to center # 0
We recount the center # 0: 150 20 200
Distance from pixel 3 to the center # 0: 216.894
Distance from pixel 3 to the center. # 1: 83.933
Distance from pixel 3 to the center # 2: 174.19
Minimum distance to center # 1
We recount the center # 1: 215.25 122.75 38.75
Distance from pixel 4 to center # 0: 208.149
The distance from pixel 4 to the center # 1: 128.622
Pixel distance 4 to center # 2: 4.58258
Minimum distance to center # 2
We recount the center # 2: 102 69.5 2
Distance from pixel 5 to the center # 0: 10.6301
Distance from pixel 5 to the center # 1: 208.212
Distance from pixel 5 to the center # 2: 219.366
Minimum distance to center # 0
We recount the center # 0: 151.5 21 205
Distance from pixel 6 to center # 0: 215.848
Distance from pixel 6 to the center # 1: 42.6109
Distance from pixel 6 to the center. # 2: 172.905
Minimum distance to center # 1
We recount the center # 1: 233.625 130.375 46.375
Distance from pixel 7 to center # 0: 213.916
Distance from pixel 7 to center # 1: 150.21
Distance from pixel 7 to center # 2: 5.02494
Minimum distance to center # 2
We recount center # 2: 101.5 71.75 3
Perform pixel classification:
Distance from pixel number 0 to the center # 0: 221.129
Distance from pixel # 0 to center # 1: 23.7207
Distance from pixel # 0 to center # 2: 174.44
Pixel number 0 closest to the center # 1
Distance from pixel number 1 to the center # 0: 216.031
Distance from pixel number 1 to the center # 1: 153.492
Distance from pixel number 1 to the center # 2: 3.05164
Pixel number 1 closest to the center # 2
Distance from pixel number 2 to the center # 0: 5.31507
Distance from pixel number 2 to the center # 1: 206.825
Distance from pixel number 2 to the center # 2: 209.378
Pixel number 2 closest to the center # 0
Distance from pixel number 3 to the center # 0: 219.126
Distance from pixel number 3 to the center # 1: 20.8847
Distance from pixel number 3 to the center # 2: 171.609
Pixel number 3 closest to the center # 1
Distance from pixel number 4 to the center # 0: 212.989
Distance from pixel number 4 to the center # 1: 149.836
Distance from pixel number 4 to the center # 2: 3.71652
Pixel number 4 closest to the center # 2
Distance from pixel number 5 to the center # 0: 5.31507
Distance from pixel number 5 to the center # 1: 212.176
Distance from pixel number 5 to the center # 2: 219.035
Pixel number 5 closest to the center # 0
Distance from pixel number 6 to the center # 0: 215.848
Distance from pixel number 6 to the center # 1: 21.3054
Distance from pixel number 6 to the center # 2: 172.164
Pixel number 6 closest to the center # 1
Distance from pixel number 7 to the center # 0: 213.916
Distance from pixel number 7 to the center # 1: 150.21
Distance from pixel number 7 to the center # 2: 2.51247
Pixel number 7 closest to the center # 2
Array of matching pixels and centers:
1 2 0 1 2 0 1 2
Clustering result:
Cluster # 0
150 20 200
153 22 210
Cluster # 1
255 140 50
251 141 51
252 138 54
Cluster # 2
100 70 1
104 69 3
101 74 4
New centers:
151.5 21 205 - # 0
233.625 130.375 46.375 - # 1
101.5 71.75 3 - # 2
Iteration # 1
Distance from pixel 0 to center # 0: 221.129
Distance from pixel 0 to center # 1: 23.7207
Distance from pixel 0 to center # 2: 174.44
Minimum distance to center # 1
We recount the center # 1: 244.313 135.188 48.1875
Distance from pixel 1 to center # 0: 216.031
The distance from pixel 1 to the center # 1: 165.234
Distance from pixel 1 to the center # 2: 3.05164
Minimum distance to center # 2
We recount the center # 2: 100.75 70.875 2
The distance from pixel 2 to the center # 0: 5.31507
The distance from pixel 2 to the center # 1: 212.627
The distance from pixel 2 to the center # 2: 210.28
Minimum distance to center # 0
We recount the center # 0: 150.75 20.5 202.5
Distance from pixel 3 to center # 0: 217.997
Distance from pixel 3 to the center. # 1: 9.29613
Distance from pixel 3 to the center. # 2: 172.898
Minimum distance to center # 1
We recount the center # 1: 247.656 138.094 49.5938
The distance from pixel 4 to the center # 0: 210.566
Distance from pixel 4 to center # 1: 166.078
Distance from pixel 4 to the center. # 2: 3.88306
Minimum distance to center # 2
We recount the center # 2: 102.375 69.9375 2.5
Distance from pixel 5 to the center # 0: 7.97261
Distance from pixel 5 to the center # 1: 219.471
Distance from pixel 5 to the center. # 2: 218.9
Minimum distance to center # 0
We recount the center # 0: 151.875 21.25 206.25
Distance from pixel 6 to center # 0: 216.415
Distance from pixel 6 to the center # 1: 6.18805
The distance from pixel 6 to the center # 2: 172.257
Minimum distance to center # 1
We recount the center # 1: 249.828 138.047 51.7969
Distance from pixel 7 to center # 0: 215.118
Distance from pixel 7 to the center. # 1: 168.927
Distance from pixel 7 to the center. # 2: 4.54363
Minimum distance to center # 2
We recount the center # 2: 101.688 71.9688 3.25
Perform pixel classification:
Distance from pixel # 0 to center # 0: 221.699
Distance from pixel number 0 to the center # 1: 5.81307
Distance from pixel # 0 to center # 2: 174.122
Pixel number 0 closest to the center # 1
Distance from pixel number 1 to the center # 0: 217.244
Distance from pixel number 1 to the center # 1: 172.218
Distance from pixel number 1 to the center # 2: 3.43309
Pixel number 1 closest to the center # 2
Distance from pixel number 2 to the center # 0: 6.64384
Distance from pixel number 2 to the center # 1: 214.161
Distance from pixel number 2 to the center # 2: 209.154
Pixel number 2 closest to the center # 0
Distance from pixel number 3 to the center # 0: 219.701
Distance from pixel number 3 to the center # 1: 3.27555
Distance from pixel number 3 to the center # 2: 171.288
Pixel number 3 closest to the center # 1
Distance from pixel number 4 to the center # 0: 214.202
Distance from pixel number 4 to the center # 1: 168.566
Distance from pixel number 4 to the center # 2: 3.77142
Pixel number 4 closest to the center # 2
Distance from pixel number 5 to the center # 0: 3.9863
Distance from pixel number 5 to the center # 1: 218.794
Distance from pixel number 5 to the center # 2: 218.805
Pixel number 5 closest to the center # 0
Distance from pixel number 6 to the center # 0: 216.415
Distance from pixel number 6 to the center # 1: 3.09403
Distance from pixel number 6 to the center # 2: 171.842
Pixel number 6 closest to the center # 1
Distance from pixel number 7 to the center # 0: 215.118
Distance from pixel number 7 to the center # 1: 168.927
Distance from pixel number 7 to the center # 2: 2.27181
Pixel number 7 closest to the center # 2
Array of matching pixels and centers:
1 2 0 1 2 0 1 2
Clustering result:
Cluster # 0
150 20 200
153 22 210
Cluster # 1
255 140 50
251 141 51
252 138 54
Cluster # 2
100 70 1
104 69 3
101 74 4
New centers:
151.875 21.25 206.25 - # 0
249.828 138.047 51.7969 - # 1
101.688 71.9688 3.25 - # 2
End of clustering.
255 140 50 - №0
100 70 1 - №1
150 20 200 - №2
251 141 51 - № 3
104 69 3 - №4
153 22 210 - №5
252 138 54 - № 6
101 74 4 - №7
Random initial clustering centers:
150 20 200 - # 0
104 69 3 - # 1
100 70 1 - # 2
Number of clusters: 3
Number of pixels: 8
Start of clustering:
Iteration # 0
Distance from pixel 0 to center # 0: 218.918
Distance from pixel 0 to center # 1: 173.352
Pixel Distance 0 to Center # 2: 176.992
Minimum distance to center # 1
We recount the center # 1: 179.5 104.5 26.5
Distance from pixel 1 to center # 0: 211.189
The distance from pixel 1 to the center # 1: 90.3369
Distance from pixel 1 to center # 2: 0
Minimum distance to center # 2
We recount the center # 2: 100 70 1
Distance from pixel 2 to the center # 0: 0
Distance from pixel 2 to the center # 1: 195.225
Distance from pixel 2 to the center # 2: 211.189
Minimum distance to center # 0
We recount the center # 0: 150 20 200
Distance from pixel 3 to the center # 0: 216.894
Distance from pixel 3 to the center. # 1: 83.933
Distance from pixel 3 to the center # 2: 174.19
Minimum distance to center # 1
We recount the center # 1: 215.25 122.75 38.75
Distance from pixel 4 to center # 0: 208.149
The distance from pixel 4 to the center # 1: 128.622
Pixel distance 4 to center # 2: 4.58258
Minimum distance to center # 2
We recount the center # 2: 102 69.5 2
Distance from pixel 5 to the center # 0: 10.6301
Distance from pixel 5 to the center # 1: 208.212
Distance from pixel 5 to the center # 2: 219.366
Minimum distance to center # 0
We recount the center # 0: 151.5 21 205
Distance from pixel 6 to center # 0: 215.848
Distance from pixel 6 to the center # 1: 42.6109
Distance from pixel 6 to the center. # 2: 172.905
Minimum distance to center # 1
We recount the center # 1: 233.625 130.375 46.375
Distance from pixel 7 to center # 0: 213.916
Distance from pixel 7 to center # 1: 150.21
Distance from pixel 7 to center # 2: 5.02494
Minimum distance to center # 2
We recount center # 2: 101.5 71.75 3
Perform pixel classification:
Distance from pixel number 0 to the center # 0: 221.129
Distance from pixel # 0 to center # 1: 23.7207
Distance from pixel # 0 to center # 2: 174.44
Pixel number 0 closest to the center # 1
Distance from pixel number 1 to the center # 0: 216.031
Distance from pixel number 1 to the center # 1: 153.492
Distance from pixel number 1 to the center # 2: 3.05164
Pixel number 1 closest to the center # 2
Distance from pixel number 2 to the center # 0: 5.31507
Distance from pixel number 2 to the center # 1: 206.825
Distance from pixel number 2 to the center # 2: 209.378
Pixel number 2 closest to the center # 0
Distance from pixel number 3 to the center # 0: 219.126
Distance from pixel number 3 to the center # 1: 20.8847
Distance from pixel number 3 to the center # 2: 171.609
Pixel number 3 closest to the center # 1
Distance from pixel number 4 to the center # 0: 212.989
Distance from pixel number 4 to the center # 1: 149.836
Distance from pixel number 4 to the center # 2: 3.71652
Pixel number 4 closest to the center # 2
Distance from pixel number 5 to the center # 0: 5.31507
Distance from pixel number 5 to the center # 1: 212.176
Distance from pixel number 5 to the center # 2: 219.035
Pixel number 5 closest to the center # 0
Distance from pixel number 6 to the center # 0: 215.848
Distance from pixel number 6 to the center # 1: 21.3054
Distance from pixel number 6 to the center # 2: 172.164
Pixel number 6 closest to the center # 1
Distance from pixel number 7 to the center # 0: 213.916
Distance from pixel number 7 to the center # 1: 150.21
Distance from pixel number 7 to the center # 2: 2.51247
Pixel number 7 closest to the center # 2
Array of matching pixels and centers:
1 2 0 1 2 0 1 2
Clustering result:
Cluster # 0
150 20 200
153 22 210
Cluster # 1
255 140 50
251 141 51
252 138 54
Cluster # 2
100 70 1
104 69 3
101 74 4
New centers:
151.5 21 205 - # 0
233.625 130.375 46.375 - # 1
101.5 71.75 3 - # 2
Iteration # 1
Distance from pixel 0 to center # 0: 221.129
Distance from pixel 0 to center # 1: 23.7207
Distance from pixel 0 to center # 2: 174.44
Minimum distance to center # 1
We recount the center # 1: 244.313 135.188 48.1875
Distance from pixel 1 to center # 0: 216.031
The distance from pixel 1 to the center # 1: 165.234
Distance from pixel 1 to the center # 2: 3.05164
Minimum distance to center # 2
We recount the center # 2: 100.75 70.875 2
The distance from pixel 2 to the center # 0: 5.31507
The distance from pixel 2 to the center # 1: 212.627
The distance from pixel 2 to the center # 2: 210.28
Minimum distance to center # 0
We recount the center # 0: 150.75 20.5 202.5
Distance from pixel 3 to center # 0: 217.997
Distance from pixel 3 to the center. # 1: 9.29613
Distance from pixel 3 to the center. # 2: 172.898
Minimum distance to center # 1
We recount the center # 1: 247.656 138.094 49.5938
The distance from pixel 4 to the center # 0: 210.566
Distance from pixel 4 to center # 1: 166.078
Distance from pixel 4 to the center. # 2: 3.88306
Minimum distance to center # 2
We recount the center # 2: 102.375 69.9375 2.5
Distance from pixel 5 to the center # 0: 7.97261
Distance from pixel 5 to the center # 1: 219.471
Distance from pixel 5 to the center. # 2: 218.9
Minimum distance to center # 0
We recount the center # 0: 151.875 21.25 206.25
Distance from pixel 6 to center # 0: 216.415
Distance from pixel 6 to the center # 1: 6.18805
The distance from pixel 6 to the center # 2: 172.257
Minimum distance to center # 1
We recount the center # 1: 249.828 138.047 51.7969
Distance from pixel 7 to center # 0: 215.118
Distance from pixel 7 to the center. # 1: 168.927
Distance from pixel 7 to the center. # 2: 4.54363
Minimum distance to center # 2
We recount the center # 2: 101.688 71.9688 3.25
Perform pixel classification:
Distance from pixel # 0 to center # 0: 221.699
Distance from pixel number 0 to the center # 1: 5.81307
Distance from pixel # 0 to center # 2: 174.122
Pixel number 0 closest to the center # 1
Distance from pixel number 1 to the center # 0: 217.244
Distance from pixel number 1 to the center # 1: 172.218
Distance from pixel number 1 to the center # 2: 3.43309
Pixel number 1 closest to the center # 2
Distance from pixel number 2 to the center # 0: 6.64384
Distance from pixel number 2 to the center # 1: 214.161
Distance from pixel number 2 to the center # 2: 209.154
Pixel number 2 closest to the center # 0
Distance from pixel number 3 to the center # 0: 219.701
Distance from pixel number 3 to the center # 1: 3.27555
Distance from pixel number 3 to the center # 2: 171.288
Pixel number 3 closest to the center # 1
Distance from pixel number 4 to the center # 0: 214.202
Distance from pixel number 4 to the center # 1: 168.566
Distance from pixel number 4 to the center # 2: 3.77142
Pixel number 4 closest to the center # 2
Distance from pixel number 5 to the center # 0: 3.9863
Distance from pixel number 5 to the center # 1: 218.794
Distance from pixel number 5 to the center # 2: 218.805
Pixel number 5 closest to the center # 0
Distance from pixel number 6 to the center # 0: 216.415
Distance from pixel number 6 to the center # 1: 3.09403
Distance from pixel number 6 to the center # 2: 171.842
Pixel number 6 closest to the center # 1
Distance from pixel number 7 to the center # 0: 215.118
Distance from pixel number 7 to the center # 1: 168.927
Distance from pixel number 7 to the center # 2: 2.27181
Pixel number 7 closest to the center # 2
Array of matching pixels and centers:
1 2 0 1 2 0 1 2
Clustering result:
Cluster # 0
150 20 200
153 22 210
Cluster # 1
255 140 50
251 141 51
252 138 54
Cluster # 2
100 70 1
104 69 3
101 74 4
New centers:
151.875 21.25 206.25 - # 0
249.828 138.047 51.7969 - # 1
101.688 71.9688 3.25 - # 2
End of clustering.
This example is planned in advance, the pixels are selected specifically for demonstration. The program needs two iterations to group the data into three clusters. Looking at the centers of the last two iterations, you can see that they almost stayed in place.
More interesting cases with random pixel generation. Having generated 50 points that need to be divided into 10 clusters, I got 5 iterations. Having generated 50 points that need to be divided into 3 clusters, I got all 100 maximum allowed iterations. You can see that the more clusters, the easier it is for the program to find the most similar pixels and combine them into smaller groups, and vice versa - if there are few clusters and many points, the algorithm often ends only by exceeding the maximum allowed number of iterations, since some pixels constantly jump from one cluster to another. Nevertheless, the bulk is still defined in their clusters finally.
Well, now let's check the result of clustering. Taking the result of some clusters from the example of 50 points on 10 clusters, I hammered the result of this data into Illustrator and this is what happened:
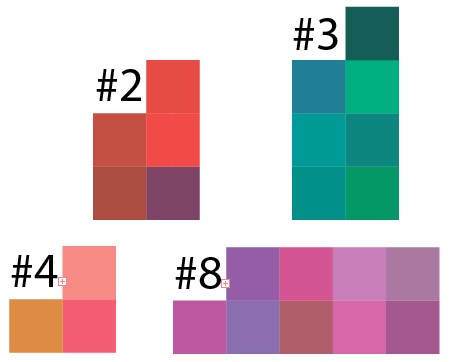
It can be seen that in each cluster any shades of color prevail, and here you need to understand that the pixels were chosen randomly; an analogue of such an image in real life is some kind of picture that was randomly sprinkled with all colors and it is difficult to isolate areas of similar colors.
Suppose we have such a photo. We can define an island as one cluster, but with an increase we see that it consists of different shades of green.

And this is the 8th cluster, but in a smaller version, the result is similar:

The full version of the program can be viewed on my GitHub .
Source: https://habr.com/ru/post/427761/
All Articles