Solvability beltway problems in polynomial time
Students get acquainted with the beltway problem by taking bioinformatics courses, in particular, one of the most qualitative and closest in spirit for programmers - the Bioinformatics course (Pavel Pevzner) at the course of the University of California San Diego. The problem draws attention to the simplicity of the statement, its practical importance, and the fact that it is still considered unsolved, with the seeming opportunity to solve it by simple coding. The problem is put this way. Is it possible to restore the coordinates of a set of points in polynomial time ? $ inline $ x $ inline $ if the set of all pair distances between them is known $ inline $ \ Delta X $ inline $ ?
This seemingly simple task is still on the list of unsolved problems of computational geometry. Moreover, the situation does not even concern points in multidimensional spaces, especially curved ones, the problem is the simplest option - when all points have integer coordinates and are localized on one line.
Over the past almost half a century since this task was perceived by mathematicians as a challenge (Shamos, 1975), some results were obtained. Consider two cases possible for a one-dimensional problem:
These two cases have received different names for a reason - various efforts are required to solve them. And indeed, the first problem was solved fairly quickly (in 15 years) and a backtracking algorithm was built, which restores the solution on average in quadratic time. $ inline $ O (n ^ 2 \ log n) $ inline $ where $ inline $ n $ inline $ - the number of points (Skiena, 1990); for the second task, this has not been done so far, and the best proposed algorithm has exponential computational complexity $ inline $ O (n ^ n \ log n) $ inline $ (Lemke, 2003). The picture below shows an estimate of how long your computer will work to get a solution for a set with a different number of points.
')

That is, for a psychologically acceptable time (~ 10 sec), you can restore a lot $ inline $ x $ inline $ up to 10 thousand points in the turnpike case and only ~ 10 points for the beltway case, which is completely useless for practical applications.
Small clarification. It is considered that the turnpike problem is solved from the point of view of use in practice, that is, for the vast majority of the data encountered. At the same time, the objections of pure mathematicians to the fact that there are special data sets for which the time of obtaining a solution is exponential are ignored. $ inline $ O (2 ^ n \ log n) $ inline $ (Zhang, 1982). In contrast to turnpike, beltway, the problem with its exponential algorithm can in no way be considered practically solved.
At the end of the 20th century, a new pathway for the synthesis of biomolecules was discovered, called the non-ribosomal synthesis pathway. Its main difference from the classical synthesis pathway is that the final result of the synthesis is not encoded in DNA at all. Instead, only the code of “tools” (many different synthetases) that these objects can collect is recorded in the DNA. Thus, biomachine engineering is substantially enriched, and a cell instead of one type of collector (ribosomes) that works with only 20 standard parts (standard amino acids, also called proteinogenic), many other types of collectors appear that can work with more than 500 standard and non-standard parts (non-proteinogenic amino acids and their various modifications). And these collectors can not only join parts into chains, but also get very intricate designs - cyclic, branching, as well as designs with many cycles and branching. All this significantly increases the cell's arsenal for different occasions of its life. The biological activity of such structures is high, the specificity (selectivity of action) is also, the variety of properties is not limited. The class of these cell products in the English-language literature is called NRPs (non-ribosomal products, or non-ribosomal peptides). Biologists hope that it is among these products of cell metabolism that one can find new pharmacological preparations that are highly effective and have no side effects due to their specificity.
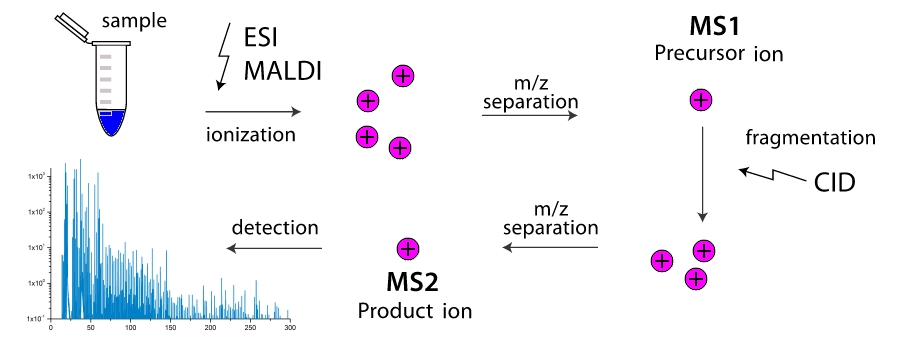
The only question is, how and where to look for NRPs? They are very effective, therefore the cell has absolutely no need to produce them in large quantities, and their concentrations are negligible. So chemical methods of extraction with their low accuracy ~ 1% and huge expenses on reagents and time are useless. Further. They are not encoded in DNA, which means all the databases that are accumulated during the decoding of the genome, and all methods of bioinformatics and genomics are also useless. The only way to find something remains physical methods, and, namely, mass spectroscopy. Moreover, the detection level of a substance in modern spectrometers is so high that it allows you to find insignificant quantities, total> ~ 800 molecules (atto-molar range, or concentration $ inline $ 10 ^ {- 18} $ inline $ ).
 "
"
And how does a mass spectrometer work? In the working chamber of the device is the destruction of molecules into fragments (more often through their collisions with each other, less often due to external influence). These fragments are ionized, and then accelerated and separated in an external electromagnetic field. The separation takes place either by the time it reaches the detector, or by the rotation angle in the magnetic field, because the greater the mass of the fragment and the lower its charge, the more clumsy it is. Thus, the mass spectrometer as if "weights" the mass of fragments. Moreover, the "weighing" can be made multi-stage by repeatedly filtering fragments with one mass (more precisely, with one value $ inline $ m / z $ inline $ ) and driving them through fragmentation with further separation. Two-stage mass spectrometers are widely distributed and are called tandem, multistage mass spectrometers are extremely rare, and are simply referred to as $ inline $ ms ^ n $ inline $ where $ inline $ n $ inline $ - number of stages. And here the task appears, knowing only the masses of various fragments of a molecule to know its structure? Here we come to turnpike and beltway problems, for linear and cyclic peptides, respectively.
Let me explain in more detail how the task of restoring the structure of a biomolecule is reduced to these problems using the example of a cyclic peptide.
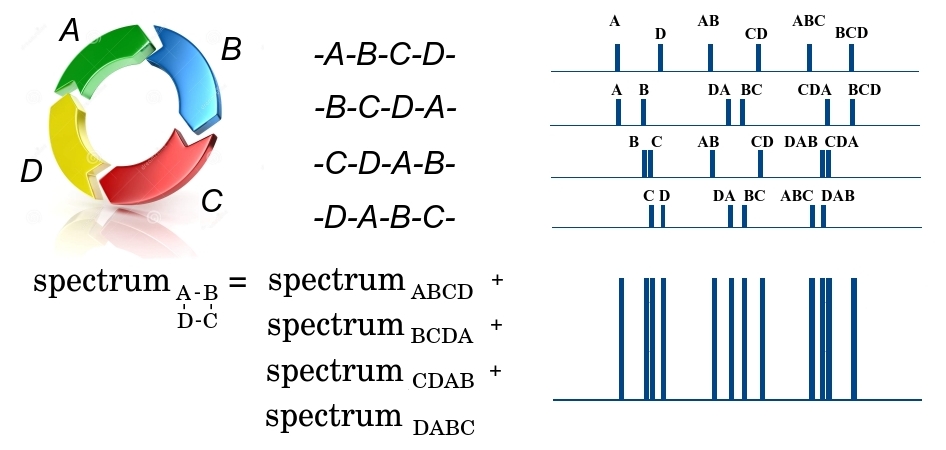
The cyclic ABCD peptide at the first stage of fragmentation can be broken in 4 places, either by the DA bond, or by AB, BC or CD, forming 4 possible linear peptides - either ABCD, BCDA, CDAB or DABC. Since a huge number of identical peptides pass through the spectrometer, then at the output we will have fragments of all 4 types. Moreover, we note that all the fragments have the same mass and cannot be separated at the first stage. At the second stage, the linear fragment of ABCD can be broken in three places, forming smaller fragments with different masses A and BCD, AB and CD, ABC and D, and forming the corresponding mass spectrum. In this spectrum, the fragment mass is deposited along the x axis, and the number of small fragments with a given mass along the y axis. Similarly, the spectra are formed for the remaining three linear fragments of BCDA, CDAB and DABC. Since all 4 large fragments passed to the second stage, all their spectra are added. Total, on an output some set of masses turns out $ inline $ \ {m_1 ^ {n_1}, m_2 ^ {n_2}, .., m_q ^ {n_q} \} $ inline $ where $ inline $ m_i $ inline $ - some mass, and $ inline $ n_i $ inline $ - the multiplicity of its repetition. At the same time, we do not know which fragment this mass belongs to or whether this fragment is unique, since different fragments can have the same mass. The further the bonds in the peptide are from each other, the greater the mass of the peptide fragment is between them. That is, the task of restoring the order of elements in a cyclic peptide is reduced to a beltway problem, in which the elements of the set $ inline $ x $ inline $ are bonds in the peptide, and elements of the set $ inline $ \ Delta X $ inline $ - masses of fragments between bonds.
From my own experience and from communication with people who tried or actually did something to solve this problem, I noticed that the vast majority of people try to solve it either in general, or for integer data in a narrow range, like this (1, 50). Both options are doomed to failure. For the general case, it was proved that the total number of solutions for beltway problems in the one-dimensional case $ inline $ S_1 (n) $ inline $ limited to values (Lemke, 2003)
Learning about these facts, you can put up and give up on this task. I admit that this is one of the reasons why the beltway problem is still considered unsolved. However, loopholes do exist. Recall that the exponential function $ inline $ e ^ {\ alpha x} $ inline $ behaves very interesting. At first, it grows scary slowly, rising from 0 to 1 for an infinitely large interval from $ inline $ \ infty $ inline $ to 0, then its growth accelerates more and more. However, the smaller the value $ inline $ \ alpha $ inline $ the greater should be the value $ inline $ x $ inline $ so that the result of the function transcends a specified value $ inline $ y = \ xi $ inline $ . As such a value is convenient to choose the number $ inline $ \ xi = 2 $ inline $ , before it is the only solution, after it there are many solutions. Question. Did anyone check the dependence of the number of decisions on what data go into the input? Yes, I did. There is a remarkable phD dissertation of a Croatian woman mathematician Tamara Dakis (Dakic, 2000), in which she defined what conditions the input data should satisfy in order for the problem to be solved in polynomial time. The most important of them are the uniqueness of the solution and the absence of duplication in the set of input data $ inline $ \ Delta X $ inline $ . The level of her phD dissertation is very high. It is a pity that this student was limited only by the turnpike problem, convinced that she would have turned her interest in the beltway problem a long time ago.
Detect data for which it is possible to build the desired algorithm by accident. It took additional ideas. The main idea arose from the observation (see above) that the spectrum of a cyclic peptide is the sum of the spectra of all linear peptides that are formed during single ring breaks. Since the amino acid sequence in a peptide can be recovered from any such linear peptide, the total number of lines in the spectrum is significant (in $ inline $ n $ inline $ time where $ inline $ n $ inline $ - the number of amino acids in the peptide) is excessive. The only question is which lines need to be excluded from the spectrum in order not to lose the possibility of restoring the sequence. Since mathematically both tasks (recovery of a cyclic peptide sequence from the mass spectrum and the beltway problem) are isomorphic, it is also possible to puncture many $ inline $ \ Delta X $ inline $ .
Thinning operations $ inline $ \ Delta X $ inline $ were built using local symmetries of the set $ inline $ \ Delta X $ inline $ (Fomin, 2016a).
Theorems have been proved that both operations thin out many $ inline $ \ Delta X $ inline $ but there will still be enough elements in it to restore the solution $ inline $ x $ inline $ . Using these, the operation was built and implemented on the c ++ algorithm to solve the beltway problem (Fomin, 2016b). The algorithm differs little from the classical backtracking algorithm (that is, we try to build a solution by iterating through possible options and make returns if we get an error during the construction). The only difference is that for the account of the narrowing of the set $ inline $ \ Delta X $ inline $ Trying us becomes significantly less options.
Here is an example of how many $ inline $ \ Delta X $ inline $ when thinning.

Computational experiments were performed for randomly generated cyclic peptides of length $ inline $ n $ inline $ from 10 to 1000 amino acids (y-axis on a logarithmic scale). The abscissa axis also on a logarithmic scale shows the number of elements in sets thinned out by different operations. $ inline $ \ Delta X $ inline $ in units $ inline $ n $ inline $ . Such a presentation is absolutely unusual, because I will decipher how it is read by example. Look at the left chart. Let the peptide have a length $ inline $ n = 100 $ inline $ . For him, the number of elements in the set $ inline $ \ Delta X $ inline $ equally $ inline $ n ^ 2 = 10000 $ inline $ (this is the point on the upper dotted straight line $ inline $ y = n ^ 2 $ inline $ ). After removing from the set $ inline $ \ Delta X $ inline $ duplicate elements, number of elements in $ inline $ \ Delta X $ inline $ reduced to $ inline $ n_D \ approx n ^ {1.9} \ approx 6300 $ inline $ (circles with crosses). After symmetrization the number of elements falls to $ inline $ n_S \ approx n ^ {1.75} \ approx 3100 $ inline $ (black circles), and after the convolution by partial solution before $ inline $ n_C \ approx n ^ {1.35} \ approx 500 $ inline $ (crosses). Total amount of the set $ inline $ \ Delta X $ inline $ reduced by only 20 times. For a peptide of the same length, but in the right diagram, the reduction is from $ inline $ n ^ 2 = 10000 $ inline $ before $ inline $ N_C \ approx n \ approx 100 $ inline $ that is 100 times.
Note that the generation of test examples for the left diagram is done in such a way that the level of duplication $ inline $ k_ {dup} $ inline $ at $ inline $ \ Delta X $ inline $ was in the range from 0.1 to 0.3, and for the right - less than 0.1. The level of duplication is defined as $ inline $ k_ {dup} = 2- \ log {N_u} / \ log {n} $ inline $ where $ inline $ N_u $ inline $ - the number of unique elements in the set $ inline $ \ Delta X $ inline $ . This definition gives a natural result: in the absence of duplicates in the set $ inline $ \ Delta X $ inline $ its power is equal to $ inline $ N_u = n ^ 2 $ inline $ and $ inline $ k_ {dup} = 0 $ inline $ , with the greatest possible duplication $ inline $ N_u = n $ inline $ and $ inline $ k_ {dup} = 1 $ inline $ . How to make provide a different level of duplication, I will say a little later. The diagrams show that the lower the level of duplication, the more thinned out $ inline $ \ Delta X $ inline $ at $ inline $ k_ {dup} <0.1 $ inline $ number of elements in thinned $ inline $ \ Delta X $ inline $ generally reaches its limit $ inline $ O (n ^ 2) \ rightarrow O (n) $ inline $ because the thinned set is less than $ inline $ O (n) $ inline $ elements cannot be obtained (operations retain enough elements to obtain a solution in which $ inline $ n $ inline $ elements). The fact of narrowing the power set $ inline $ \ Delta X $ inline $ to the lower limit is very important, it leads to dramatic changes in the computational complexity of obtaining a solution.
After inserting thinning operations into the backtracking algorithm and in solving the beltway problem, a complete analog of what Tamara Dakis was talking about with respect to the turnpike problem was revealed. I will remind you. She said that for turnpike problems it is possible to get a solution in polynomial time if the solution is unique and there is no duplication in $ inline $ \ Delta X $ inline $ . It turned out that a complete lack of duplication is not necessarily necessary (it is hardly possible for real data), it is enough that its level will be sufficiently small. The figure below shows how long it takes to get a solution to the beltway problem depending on the peptide length and the level of duplication in $ inline $ \ Delta X $ inline $ .

In the figure, both the x-axis and y-axis are given on a logarithmic scale. This allows you to clearly see whether the dependence of the count time on the sequence $ inline $ t = f (n) $ inline $ exponential (straight line) or polynomial (log-shaped curve). As can be seen in the diagrams, with a low level of duplication (right diagram), the solution is obtained in polynomial time. Well, to be more precise, the solution is obtained in quadratic time. This occurs when thinning operations reduce the power of the set to a lower limit. $ inline $ O (n ^ 2) \ rightarrow O (n) $ inline $ , there are few points left in it, returns when searching for options become single, and as a matter of fact, the algorithm ceases to sort out the options, but simply constructs a solution from what is left.
PS Well, I will reveal the last secret regarding the generation of sets in different levels of duplication. This is due to the different accuracy of data presentation. If the data is generated with low accuracy (for example, rounding to integers), then the level of duplication becomes high, more than 0.3. If the data is generated with good accuracy, for example, up to 3 decimal places, the level of duplication decreases sharply, less than 0.1. And from here follows the last most important remark.
For real data, in conditions of constantly increasing measurement accuracy, the beltway problem becomes solvable in real time.
Literature.
1. Dakic, T. (2000). On the Turnpike Problem. PhD thesis, Simon Fraser University.
2. Fomin. E. (2016a) A Pair of Distances in the Sequence of Sequencing Problem: I. Theory. J Comput Biol. 2016, 23 (9): 769-75.
3. Fomin. E. (2016b) wise Appro ^ Pair ps 2 wise ps wise Pair 2 wise Pair 2 2 wise II 2 2 Algorithm. J Comput Biol. 2016, 23 (12): 934-942.
4. Lemke, P., Skiena, S., and Smith, W. (2003). Reconstructing Sets From Interpoint Distances. Discrete and Computational Geometry Algorithms and Combinatorics, 25: 597–631.
5. Skiena, S., Smith, W., and Lemke, P. (1990). Reconstructing sets from interpoint distances. In Proceedings of the Sixth ACM Symposium on Computational Geometry, pages 332–339. Berkeley, CA
6. Zhang, Z. 1982. An example of a partial digest mapping algorithm. J. Comp. Biol. 1, 235–240.
This seemingly simple task is still on the list of unsolved problems of computational geometry. Moreover, the situation does not even concern points in multidimensional spaces, especially curved ones, the problem is the simplest option - when all points have integer coordinates and are localized on one line.
Over the past almost half a century since this task was perceived by mathematicians as a challenge (Shamos, 1975), some results were obtained. Consider two cases possible for a one-dimensional problem:
- points are located on a straight line (turnpike problem)
- points are located on a circle (beltway problem)
These two cases have received different names for a reason - various efforts are required to solve them. And indeed, the first problem was solved fairly quickly (in 15 years) and a backtracking algorithm was built, which restores the solution on average in quadratic time. $ inline $ O (n ^ 2 \ log n) $ inline $ where $ inline $ n $ inline $ - the number of points (Skiena, 1990); for the second task, this has not been done so far, and the best proposed algorithm has exponential computational complexity $ inline $ O (n ^ n \ log n) $ inline $ (Lemke, 2003). The picture below shows an estimate of how long your computer will work to get a solution for a set with a different number of points.
')

That is, for a psychologically acceptable time (~ 10 sec), you can restore a lot $ inline $ x $ inline $ up to 10 thousand points in the turnpike case and only ~ 10 points for the beltway case, which is completely useless for practical applications.
Small clarification. It is considered that the turnpike problem is solved from the point of view of use in practice, that is, for the vast majority of the data encountered. At the same time, the objections of pure mathematicians to the fact that there are special data sets for which the time of obtaining a solution is exponential are ignored. $ inline $ O (2 ^ n \ log n) $ inline $ (Zhang, 1982). In contrast to turnpike, beltway, the problem with its exponential algorithm can in no way be considered practically solved.
The importance of solving beltway problems in terms of bioinformatics
At the end of the 20th century, a new pathway for the synthesis of biomolecules was discovered, called the non-ribosomal synthesis pathway. Its main difference from the classical synthesis pathway is that the final result of the synthesis is not encoded in DNA at all. Instead, only the code of “tools” (many different synthetases) that these objects can collect is recorded in the DNA. Thus, biomachine engineering is substantially enriched, and a cell instead of one type of collector (ribosomes) that works with only 20 standard parts (standard amino acids, also called proteinogenic), many other types of collectors appear that can work with more than 500 standard and non-standard parts (non-proteinogenic amino acids and their various modifications). And these collectors can not only join parts into chains, but also get very intricate designs - cyclic, branching, as well as designs with many cycles and branching. All this significantly increases the cell's arsenal for different occasions of its life. The biological activity of such structures is high, the specificity (selectivity of action) is also, the variety of properties is not limited. The class of these cell products in the English-language literature is called NRPs (non-ribosomal products, or non-ribosomal peptides). Biologists hope that it is among these products of cell metabolism that one can find new pharmacological preparations that are highly effective and have no side effects due to their specificity.
The only question is, how and where to look for NRPs? They are very effective, therefore the cell has absolutely no need to produce them in large quantities, and their concentrations are negligible. So chemical methods of extraction with their low accuracy ~ 1% and huge expenses on reagents and time are useless. Further. They are not encoded in DNA, which means all the databases that are accumulated during the decoding of the genome, and all methods of bioinformatics and genomics are also useless. The only way to find something remains physical methods, and, namely, mass spectroscopy. Moreover, the detection level of a substance in modern spectrometers is so high that it allows you to find insignificant quantities, total> ~ 800 molecules (atto-molar range, or concentration $ inline $ 10 ^ {- 18} $ inline $ ).
 "
"And how does a mass spectrometer work? In the working chamber of the device is the destruction of molecules into fragments (more often through their collisions with each other, less often due to external influence). These fragments are ionized, and then accelerated and separated in an external electromagnetic field. The separation takes place either by the time it reaches the detector, or by the rotation angle in the magnetic field, because the greater the mass of the fragment and the lower its charge, the more clumsy it is. Thus, the mass spectrometer as if "weights" the mass of fragments. Moreover, the "weighing" can be made multi-stage by repeatedly filtering fragments with one mass (more precisely, with one value $ inline $ m / z $ inline $ ) and driving them through fragmentation with further separation. Two-stage mass spectrometers are widely distributed and are called tandem, multistage mass spectrometers are extremely rare, and are simply referred to as $ inline $ ms ^ n $ inline $ where $ inline $ n $ inline $ - number of stages. And here the task appears, knowing only the masses of various fragments of a molecule to know its structure? Here we come to turnpike and beltway problems, for linear and cyclic peptides, respectively.
Let me explain in more detail how the task of restoring the structure of a biomolecule is reduced to these problems using the example of a cyclic peptide.

The cyclic ABCD peptide at the first stage of fragmentation can be broken in 4 places, either by the DA bond, or by AB, BC or CD, forming 4 possible linear peptides - either ABCD, BCDA, CDAB or DABC. Since a huge number of identical peptides pass through the spectrometer, then at the output we will have fragments of all 4 types. Moreover, we note that all the fragments have the same mass and cannot be separated at the first stage. At the second stage, the linear fragment of ABCD can be broken in three places, forming smaller fragments with different masses A and BCD, AB and CD, ABC and D, and forming the corresponding mass spectrum. In this spectrum, the fragment mass is deposited along the x axis, and the number of small fragments with a given mass along the y axis. Similarly, the spectra are formed for the remaining three linear fragments of BCDA, CDAB and DABC. Since all 4 large fragments passed to the second stage, all their spectra are added. Total, on an output some set of masses turns out $ inline $ \ {m_1 ^ {n_1}, m_2 ^ {n_2}, .., m_q ^ {n_q} \} $ inline $ where $ inline $ m_i $ inline $ - some mass, and $ inline $ n_i $ inline $ - the multiplicity of its repetition. At the same time, we do not know which fragment this mass belongs to or whether this fragment is unique, since different fragments can have the same mass. The further the bonds in the peptide are from each other, the greater the mass of the peptide fragment is between them. That is, the task of restoring the order of elements in a cyclic peptide is reduced to a beltway problem, in which the elements of the set $ inline $ x $ inline $ are bonds in the peptide, and elements of the set $ inline $ \ Delta X $ inline $ - masses of fragments between bonds.
Anticipation of the possibility of the existence of an algorithm with a polynomial time to solve beltway problems
From my own experience and from communication with people who tried or actually did something to solve this problem, I noticed that the vast majority of people try to solve it either in general, or for integer data in a narrow range, like this (1, 50). Both options are doomed to failure. For the general case, it was proved that the total number of solutions for beltway problems in the one-dimensional case $ inline $ S_1 (n) $ inline $ limited to values (Lemke, 2003)
$$ display $$ e ^ {2 ^ {\ frac {\ ln n} {\ ln \ ln n} + o (1)}} \ leq S_1 (n) \ leq \ frac {1} {2} n ^ {n-2} $$ display $$
which means the existence of an exponential number of solutions in the asymptotics $ inline $ n \ rightarrow \ infty $ inline $ . Obviously, if the number of solutions grows exponentially, then the time to obtain them cannot grow more slowly. That is, for the general case, a polynomial time solution is impossible. As for the integer data in a narrow range, here everything can be checked experimentally, since it is not too difficult to write code that searches for a solution using the exhaustive search method. For small $ inline $ n $ inline $ This code will not take very long. The results of testing such a code will show that, under such conditions, for data a complete number of different solutions for any set $ inline $ \ Delta X $ inline $ already at small $ inline $ n $ inline $ also growing extremely sharply.Learning about these facts, you can put up and give up on this task. I admit that this is one of the reasons why the beltway problem is still considered unsolved. However, loopholes do exist. Recall that the exponential function $ inline $ e ^ {\ alpha x} $ inline $ behaves very interesting. At first, it grows scary slowly, rising from 0 to 1 for an infinitely large interval from $ inline $ \ infty $ inline $ to 0, then its growth accelerates more and more. However, the smaller the value $ inline $ \ alpha $ inline $ the greater should be the value $ inline $ x $ inline $ so that the result of the function transcends a specified value $ inline $ y = \ xi $ inline $ . As such a value is convenient to choose the number $ inline $ \ xi = 2 $ inline $ , before it is the only solution, after it there are many solutions. Question. Did anyone check the dependence of the number of decisions on what data go into the input? Yes, I did. There is a remarkable phD dissertation of a Croatian woman mathematician Tamara Dakis (Dakic, 2000), in which she defined what conditions the input data should satisfy in order for the problem to be solved in polynomial time. The most important of them are the uniqueness of the solution and the absence of duplication in the set of input data $ inline $ \ Delta X $ inline $ . The level of her phD dissertation is very high. It is a pity that this student was limited only by the turnpike problem, convinced that she would have turned her interest in the beltway problem a long time ago.
Obtaining a polynomial algorithm for solving beltway problems
Detect data for which it is possible to build the desired algorithm by accident. It took additional ideas. The main idea arose from the observation (see above) that the spectrum of a cyclic peptide is the sum of the spectra of all linear peptides that are formed during single ring breaks. Since the amino acid sequence in a peptide can be recovered from any such linear peptide, the total number of lines in the spectrum is significant (in $ inline $ n $ inline $ time where $ inline $ n $ inline $ - the number of amino acids in the peptide) is excessive. The only question is which lines need to be excluded from the spectrum in order not to lose the possibility of restoring the sequence. Since mathematically both tasks (recovery of a cyclic peptide sequence from the mass spectrum and the beltway problem) are isomorphic, it is also possible to puncture many $ inline $ \ Delta X $ inline $ .
Thinning operations $ inline $ \ Delta X $ inline $ were built using local symmetries of the set $ inline $ \ Delta X $ inline $ (Fomin, 2016a).
- Symmetrization. The first operation is to select an arbitrary element of the set $ inline $ x _ {\ mu} \ in \ Delta X $ inline $ and remove from $ inline $ \ Delta X $ inline $ all elements except those that have symmetric pairs with respect to points $ inline $ x _ {\ mu} / 2 $ inline $ and $ inline $ (L + x _ {\ mu}) / 2 $ inline $ where $ inline $ L $ inline $ - the circumference (I remind you that in the beltway case all points are located on the circle).
- Partial solution convolution. The second operation uses the presence of a guess about the solution, that is, knowledge of individual points that belong to the solution, the so-called partial solution. Here from the set $ inline $ \ Delta X $ inline $ all elements are also deleted, except those that satisfy the condition - if we measure the distances from the point being checked to all points of the partial solution, then all the obtained values are in $ inline $ \ Delta X $ inline $ . I will specify that if at least one of the distances obtained is absent in $ inline $ \ Delta X $ inline $ then the dot is ignored.
Theorems have been proved that both operations thin out many $ inline $ \ Delta X $ inline $ but there will still be enough elements in it to restore the solution $ inline $ x $ inline $ . Using these, the operation was built and implemented on the c ++ algorithm to solve the beltway problem (Fomin, 2016b). The algorithm differs little from the classical backtracking algorithm (that is, we try to build a solution by iterating through possible options and make returns if we get an error during the construction). The only difference is that for the account of the narrowing of the set $ inline $ \ Delta X $ inline $ Trying us becomes significantly less options.
Here is an example of how many $ inline $ \ Delta X $ inline $ when thinning.

Computational experiments were performed for randomly generated cyclic peptides of length $ inline $ n $ inline $ from 10 to 1000 amino acids (y-axis on a logarithmic scale). The abscissa axis also on a logarithmic scale shows the number of elements in sets thinned out by different operations. $ inline $ \ Delta X $ inline $ in units $ inline $ n $ inline $ . Such a presentation is absolutely unusual, because I will decipher how it is read by example. Look at the left chart. Let the peptide have a length $ inline $ n = 100 $ inline $ . For him, the number of elements in the set $ inline $ \ Delta X $ inline $ equally $ inline $ n ^ 2 = 10000 $ inline $ (this is the point on the upper dotted straight line $ inline $ y = n ^ 2 $ inline $ ). After removing from the set $ inline $ \ Delta X $ inline $ duplicate elements, number of elements in $ inline $ \ Delta X $ inline $ reduced to $ inline $ n_D \ approx n ^ {1.9} \ approx 6300 $ inline $ (circles with crosses). After symmetrization the number of elements falls to $ inline $ n_S \ approx n ^ {1.75} \ approx 3100 $ inline $ (black circles), and after the convolution by partial solution before $ inline $ n_C \ approx n ^ {1.35} \ approx 500 $ inline $ (crosses). Total amount of the set $ inline $ \ Delta X $ inline $ reduced by only 20 times. For a peptide of the same length, but in the right diagram, the reduction is from $ inline $ n ^ 2 = 10000 $ inline $ before $ inline $ N_C \ approx n \ approx 100 $ inline $ that is 100 times.
Note that the generation of test examples for the left diagram is done in such a way that the level of duplication $ inline $ k_ {dup} $ inline $ at $ inline $ \ Delta X $ inline $ was in the range from 0.1 to 0.3, and for the right - less than 0.1. The level of duplication is defined as $ inline $ k_ {dup} = 2- \ log {N_u} / \ log {n} $ inline $ where $ inline $ N_u $ inline $ - the number of unique elements in the set $ inline $ \ Delta X $ inline $ . This definition gives a natural result: in the absence of duplicates in the set $ inline $ \ Delta X $ inline $ its power is equal to $ inline $ N_u = n ^ 2 $ inline $ and $ inline $ k_ {dup} = 0 $ inline $ , with the greatest possible duplication $ inline $ N_u = n $ inline $ and $ inline $ k_ {dup} = 1 $ inline $ . How to make provide a different level of duplication, I will say a little later. The diagrams show that the lower the level of duplication, the more thinned out $ inline $ \ Delta X $ inline $ at $ inline $ k_ {dup} <0.1 $ inline $ number of elements in thinned $ inline $ \ Delta X $ inline $ generally reaches its limit $ inline $ O (n ^ 2) \ rightarrow O (n) $ inline $ because the thinned set is less than $ inline $ O (n) $ inline $ elements cannot be obtained (operations retain enough elements to obtain a solution in which $ inline $ n $ inline $ elements). The fact of narrowing the power set $ inline $ \ Delta X $ inline $ to the lower limit is very important, it leads to dramatic changes in the computational complexity of obtaining a solution.
After inserting thinning operations into the backtracking algorithm and in solving the beltway problem, a complete analog of what Tamara Dakis was talking about with respect to the turnpike problem was revealed. I will remind you. She said that for turnpike problems it is possible to get a solution in polynomial time if the solution is unique and there is no duplication in $ inline $ \ Delta X $ inline $ . It turned out that a complete lack of duplication is not necessarily necessary (it is hardly possible for real data), it is enough that its level will be sufficiently small. The figure below shows how long it takes to get a solution to the beltway problem depending on the peptide length and the level of duplication in $ inline $ \ Delta X $ inline $ .

In the figure, both the x-axis and y-axis are given on a logarithmic scale. This allows you to clearly see whether the dependence of the count time on the sequence $ inline $ t = f (n) $ inline $ exponential (straight line) or polynomial (log-shaped curve). As can be seen in the diagrams, with a low level of duplication (right diagram), the solution is obtained in polynomial time. Well, to be more precise, the solution is obtained in quadratic time. This occurs when thinning operations reduce the power of the set to a lower limit. $ inline $ O (n ^ 2) \ rightarrow O (n) $ inline $ , there are few points left in it, returns when searching for options become single, and as a matter of fact, the algorithm ceases to sort out the options, but simply constructs a solution from what is left.
PS Well, I will reveal the last secret regarding the generation of sets in different levels of duplication. This is due to the different accuracy of data presentation. If the data is generated with low accuracy (for example, rounding to integers), then the level of duplication becomes high, more than 0.3. If the data is generated with good accuracy, for example, up to 3 decimal places, the level of duplication decreases sharply, less than 0.1. And from here follows the last most important remark.
For real data, in conditions of constantly increasing measurement accuracy, the beltway problem becomes solvable in real time.
Literature.
1. Dakic, T. (2000). On the Turnpike Problem. PhD thesis, Simon Fraser University.
2. Fomin. E. (2016a) A Pair of Distances in the Sequence of Sequencing Problem: I. Theory. J Comput Biol. 2016, 23 (9): 769-75.
3. Fomin. E. (2016b) wise Appro ^ Pair ps 2 wise ps wise Pair 2 wise Pair 2 2 wise II 2 2 Algorithm. J Comput Biol. 2016, 23 (12): 934-942.
4. Lemke, P., Skiena, S., and Smith, W. (2003). Reconstructing Sets From Interpoint Distances. Discrete and Computational Geometry Algorithms and Combinatorics, 25: 597–631.
5. Skiena, S., Smith, W., and Lemke, P. (1990). Reconstructing sets from interpoint distances. In Proceedings of the Sixth ACM Symposium on Computational Geometry, pages 332–339. Berkeley, CA
6. Zhang, Z. 1982. An example of a partial digest mapping algorithm. J. Comp. Biol. 1, 235–240.
Source: https://habr.com/ru/post/427759/
All Articles