Meta-clustering with error minimization, and why I think the brain works that way
Hello to all! I want to share with you my idea of machine learning.
Great achievements in the field of machine learning are impressive. Convolutional networks and LSTM are cool. But almost all modern technologies are based on the reverse propagation of error. Based on this method, it is unlikely to build a thinking machine. Neural networks are something of a frozen brain, trained once and for all, unable tochange to reflect.
I thought, why not try to create something like a living brain. A sort of reengineering. Since in all animals, despite differences in intelligence, the brain consists of approximately identical neurons, some basic principle must lie at the heart of its work.
There are several questions to which I have not found definite answers in popular literature;
')
The plausible answer to all these questions seems to me that the brain works like a multitude of simple clusterizers. Is it possible to perform such an algorithm on a group of neurons? For example, the K-means method. Completely, you just need to simplify it a bit. In the classical algorithm, the centers are calculated iteratively as the average of all the considered examples, but we will shift the center immediately after each example.
Let's see what we need to implement the clustering algorithm.
Check the resulting algorithm in practice. I scribbled a few lines on Python. This is what happens with two measurements from random numbers:

But MNIST:

At first glance, it seems that all of the above has not changed anything. Well, we had some data at the input, we somehow converted it, got other data.
But in fact there is a difference. If before the conversion, we had a bunch of analog parameters, then after the conversion we have only one parameter, with a coded unitary code. Each neuron in the group can be associated with a specific action.
I will give an example: Suppose there are only two neurons in a clustering group. Let's call them "TASTY" and "SCARY." To allow the brain to make a decision, it is necessary only to connect the neuron “EAT” to the first one, and “RUN” to the second one. For this we need a teacher. But this is not about that, training with a teacher is a topic for another article.
If you increase the number of clusters, then the accuracy will gradually increase. The extreme case is the number of clusters equal to the number of examples. But there is a problem, the number of neurons in the brain is limited. You need to constantly compromise, either accuracy or brain size.
Suppose that we have not one clustering group, but two. In this case, the inputs are fed the same values. Obviously, you get the same result.
Let's make a small random error. Let, sometimes, each clusteriser selects not the closest center of the cluster, but which one. Then the values will begin to differ, over time the difference will accumulate.

And now, let's calculate the error for each clusteriser. Error is the difference between the input example and the center of the selected cluster. If one clusteriser chooses the nearest value, and the other random, then the error of the second will be greater.
Go ahead, add a mask to the input of each clusteriser. A mask is a set of coefficients for each input. Not zero or one, as commonly used in masks, but a real number from zero to one.
Before giving an example to the input of the clusterer, we will multiply this example by the mask. For example, if a mask is used for a picture, then if for some pixel the mask is equal to one, then it is as if completely transparent. And if the mask is zero, then this pixel is always black. And if the mask is 1/2, then the pixel is darkened by half.
And now the main action, we will reduce the mask value in proportion to the error of the clusterizer. That is, if the error is large, then we will reduce the value more strongly, and if it is zero, then we will not reduce it at all.
To ensure that the values of the masks are not gradually zeroed, we will normalize them. That is, the sum of the values of the masks for each input parameter is always one. If something is taken away in one mask, this is added to another.
Let's try to see what happens by the example of MNIST. We see that the masks gradually divide the pixels into two parts.
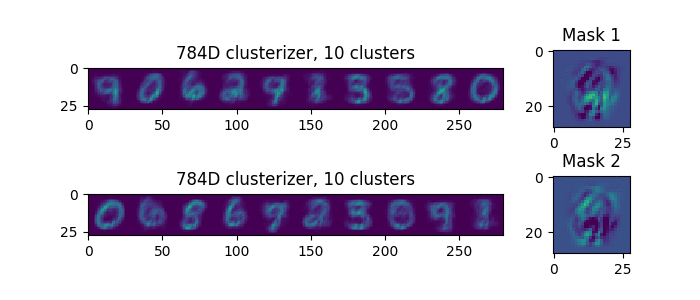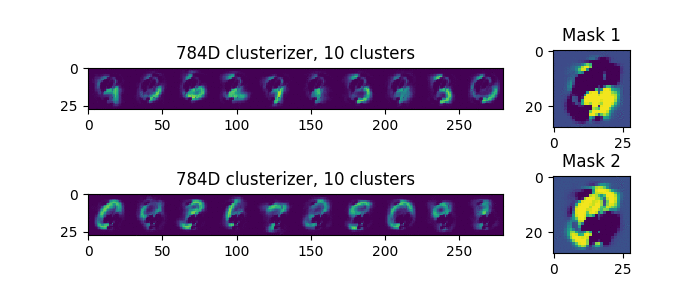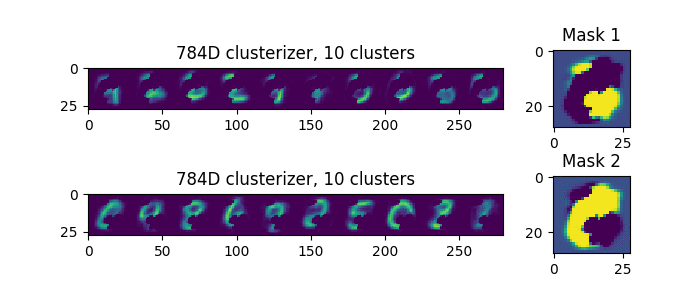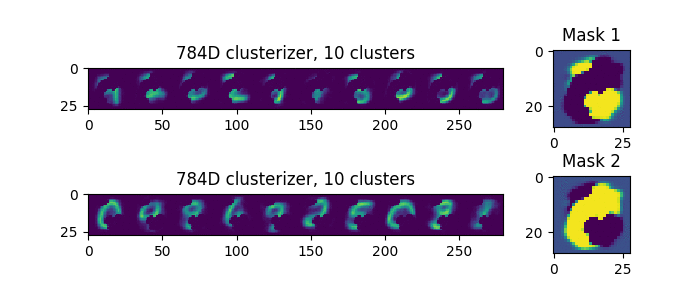
The right side of the picture shows the resulting masks. At the end of the process, the top clusteriser examines the bottom right, and the bottom clusteriser considers the rest of the examples being submitted. Interestingly, if we rerun the process, we’ll get another separation. But at the same time, the groups of parameters are not obtained as they were, but so as to reduce the prediction error. Clusterizers, as it were, try on each pixel to their mask, and at the same time, the pixel takes that clusterizer to which the pixel fits better.
Let's try to submit to the input double numbers, not superimposed on each other, but located side by side, here are the ones (this is one example, not two):

Now we see that every time, the separation is the same. That is, if there is a single, clearly the best way to separate the masks, then it will be selected.

Only one will be random, whether the first mask chooses the left figure or the right one.
I call the resulting masks meta-clusters. And the process of forming masks by meta-clustering. Why meta? Because clustering is not the input examples, but the inputs themselves.
The example is more complicated. Let's try to divide 25 parameters into 5 meta-clusters.
To do this, take five groups of five parameters, encoded with a unitary code.
That is, in each group one and only one unit in a random place. In each given example, always five units.
In the pictures below, each column is an input parameter, and each row is a meta-cluster mask. The clusters themselves are not shown.

100 parameters and 10 meta clusters:
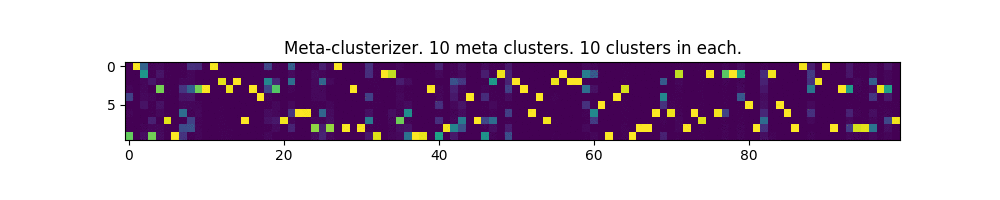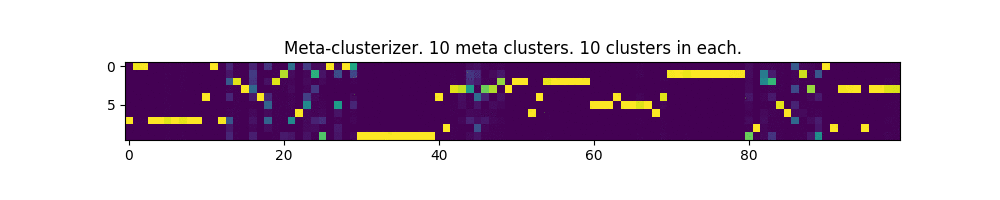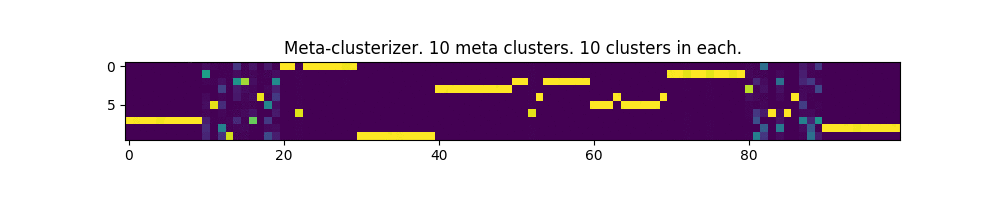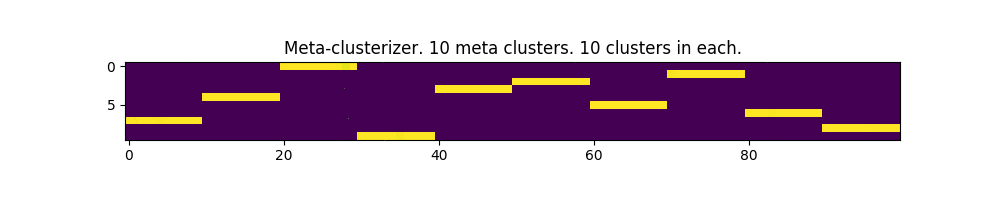
Works! In some places, even a bit like the image of the matrix from the movie of the same name.
Using meta-clustering can drastically reduce the number of clusters.
For example, take ten groups of ten parameters, in each group one unit.
If we have one clusterizer (there are no meta-clusters), then we need 10 10 = 10000000000 clusters to get a zero error.
And if we have ten clusterizers, then we need only 10 * 10 = 100 clusters. This is similar to the decimal number system, no need to come up with notation for all possible numbers, you can do with ten numbers.
Meta clustering is very well parallelized. The most costly computations (comparison of the example with the cluster center) can be performed independently for each cluster. Notice, not for the clusteriser, but for the cluster.
Before that, I was talking only about dendrites, but neurons have axons. And they also learn. So, it seems that axons are masks of meta-clusters.
Add to the description of the work of the dendrites, above, another function.
Suppose that if a neuron spike occurs, all the dendrites somehow throw something into the synapse that indicates the concentration of the neurotransmitter in the dendrite. Not from an axon to a dendrite, but back. The concentration of this substance depends on the comparison error. Let, the smaller the error, the greater the amount of substance emitted. Well, the axon reacts to the amount of this substance and grows. And if the substance is small, which means a big mistake, then the axon gradually decreases.
And if axons are changed in this way from the very birth of the brain, then over time, they will only go to those groups of neurons where their spikes of these axons are needed (do not lead to big mistakes).
Example: let it be necessary to memorize human faces. Let each face be depicted using a megapixel image. Then for each person you need a neuron with a million dendrites, which is unrealistic. And now we divide all pixels into meta-clusters, such as eyes, nose, ears, and so on. Only ten such meta-clusters. Let there be ten clusters in each meta-cluster, ten variants of the nose, ten variants of the ears, and so on for everything. Now, to memorize a face, a neuron with ten dendrites is enough. This reduces the amount of memory (well, brain volume) by five orders of magnitude.
And now, if we assume that the brain consists of meta-clusters, we can try to consider from this point of view some concepts inherent in the living brain:
Clusters must be constantly trained, otherwise new data will not be processed correctly. For learning clusters in the brain, a balanced sample is needed. Let me clarify that if it is winter now, then the brain will learn only from winter examples, and the resulting clusters will gradually become relevant only to winter, and in the summer everything will be bad for this brain. What to do with it? It is necessary to submit periodically to all clusterizers not only new, but also old important examples (memories of both winter and summer). And so that these memories do not interfere with the current sensations, you need to temporarily disable the senses. In animals, this is called a dream .
Imagine the brain is seeing something small, GRAY, that is running. After meta-clustering, we have three active neurons in three meta-clusters. And thanks to the memory, the brain knows that it is delicious. Then, the brain sees something small, BLUE, that runs. But the brain does not know whether it is tasty or scary. It is enough to temporarily disable the meta-cluster where the colors are located, and only the small one that runs will remain. And the brain knows it is delicious. This is called an analogy .
Suppose the brain remembered something, and then changed the active neuron-cluster in some group to any other, while in the other meta-clusters there remains a real memory. And so, the brain has already presented something that has never seen before. And this is the imagination .
Thank you for your attention, the code is here .
Great achievements in the field of machine learning are impressive. Convolutional networks and LSTM are cool. But almost all modern technologies are based on the reverse propagation of error. Based on this method, it is unlikely to build a thinking machine. Neural networks are something of a frozen brain, trained once and for all, unable to
I thought, why not try to create something like a living brain. A sort of reengineering. Since in all animals, despite differences in intelligence, the brain consists of approximately identical neurons, some basic principle must lie at the heart of its work.
What I do not know about neurons
There are several questions to which I have not found definite answers in popular literature;
')
- Obviously, the neuron somehow reacts to neurotransmitters, but how exactly? The simple assumption that the larger the neurotransmitter, the more frequent the adhesions, obviously does not hold water. If it were so, then the triggering of a single neuron would trigger the operation of several neighbors, the next ones, and in a short time this avalanche would capture the entire brain. But in reality this does not happen, at the same time only a small part of neurons work in the brain. Why?
- Obviously, neurons are units of memory, but how do they store information? The central part of the neuron is nothing special: the nucleus of the mitochondria and the like. The axon cannot influence the spike, since the information goes only in one direction, from the nucleus. So the only thing left is dendrites. But how is information stored in them? In analog or digital form?
- Obviously, neurons somehow learn. But how exactly? Suppose that dendrites grow in those places where there was a lot of neurotransmitter just before the spike. But if this is so, then the triggered neuron will grow a little and the next time the neurotransmitter appears, it will be the thickest among the neighbors, it will absorb the most neurotransmitter and work again. And again, a little older. And so on to infinity, until you strangle all your neighbors? Is something wrong here?
- If one neuron grows, then the neighboring ones should decrease, the head is not rubber. Something should encourage the neuron to dry out. What?
Just clustering
The plausible answer to all these questions seems to me that the brain works like a multitude of simple clusterizers. Is it possible to perform such an algorithm on a group of neurons? For example, the K-means method. Completely, you just need to simplify it a bit. In the classical algorithm, the centers are calculated iteratively as the average of all the considered examples, but we will shift the center immediately after each example.
Let's see what we need to implement the clustering algorithm.
- Cluster centers, of course, are dendrites of the neurons of our group. But how to remember the information? Suppose that the unit cell of information storage in a dendrite is the volume of a dendrite branch in the region of the synapse. The thicker the branch, respectively, the greater its volume, the greater the value saved. Thus, each dendrite can memorize several analog quantities.
- Comparators to calculate the proximity of the example. It's more complicated here. Suppose that after submitting the data (the axons have thrown out the neurotransmitter), each neuron will work the faster, the more stored data (cluster center) are similar to the example (number of neurotransmitters). Note that the absolute neurotransmitter quantity does not affect the neuron response rate, but it is the proximity of the neurotransmitter quantity to the value stored in the dendrites. Suppose that if a neurotransmitter is low, then the dendrite does not give a command for a spike. Nothing happens and if there is a lot of neurotransmitter, the spike of the dendritic branch occurs earlier than that of other dendritic branches and does not reach the nucleus. But if the neurotransmitter is just right, then all the dendritic twigs will give a mini-spike at about the same time, and this wave will turn into a spike of a neuron that will follow an axon.
- Multi-input comparator allows you to compare results and select the best. Suppose that nearby neurons have an inhibitory effect on all their neighbors. So, in some group of neurons, only one can be active at a time. It is the one that worked first. Since the neurons in the group are nearby, they have the same access to all axons coming to this group. Thus, in the group, the neuron with which the stored information is closest to the considered example will work.
- The mechanism of displacement of the center in the direction of the example. Well, everything is simple. After spike of the neuron, all the dendrites of this neuron change their volume. Where the concentration of the neurotransmitter was too large, the branches grow. Where there was insufficient, the twigs are reduced. Where the concentration is just right, the volume does not change. The volumes of the branches vary slightly. But right away. The next spike is the next change.
Check the resulting algorithm in practice. I scribbled a few lines on Python. This is what happens with two measurements from random numbers:

But MNIST:

At first glance, it seems that all of the above has not changed anything. Well, we had some data at the input, we somehow converted it, got other data.
But in fact there is a difference. If before the conversion, we had a bunch of analog parameters, then after the conversion we have only one parameter, with a coded unitary code. Each neuron in the group can be associated with a specific action.
I will give an example: Suppose there are only two neurons in a clustering group. Let's call them "TASTY" and "SCARY." To allow the brain to make a decision, it is necessary only to connect the neuron “EAT” to the first one, and “RUN” to the second one. For this we need a teacher. But this is not about that, training with a teacher is a topic for another article.
If you increase the number of clusters, then the accuracy will gradually increase. The extreme case is the number of clusters equal to the number of examples. But there is a problem, the number of neurons in the brain is limited. You need to constantly compromise, either accuracy or brain size.
Meta clustering
Suppose that we have not one clustering group, but two. In this case, the inputs are fed the same values. Obviously, you get the same result.
Let's make a small random error. Let, sometimes, each clusteriser selects not the closest center of the cluster, but which one. Then the values will begin to differ, over time the difference will accumulate.

And now, let's calculate the error for each clusteriser. Error is the difference between the input example and the center of the selected cluster. If one clusteriser chooses the nearest value, and the other random, then the error of the second will be greater.
Go ahead, add a mask to the input of each clusteriser. A mask is a set of coefficients for each input. Not zero or one, as commonly used in masks, but a real number from zero to one.
Before giving an example to the input of the clusterer, we will multiply this example by the mask. For example, if a mask is used for a picture, then if for some pixel the mask is equal to one, then it is as if completely transparent. And if the mask is zero, then this pixel is always black. And if the mask is 1/2, then the pixel is darkened by half.
And now the main action, we will reduce the mask value in proportion to the error of the clusterizer. That is, if the error is large, then we will reduce the value more strongly, and if it is zero, then we will not reduce it at all.
To ensure that the values of the masks are not gradually zeroed, we will normalize them. That is, the sum of the values of the masks for each input parameter is always one. If something is taken away in one mask, this is added to another.
Let's try to see what happens by the example of MNIST. We see that the masks gradually divide the pixels into two parts.

The right side of the picture shows the resulting masks. At the end of the process, the top clusteriser examines the bottom right, and the bottom clusteriser considers the rest of the examples being submitted. Interestingly, if we rerun the process, we’ll get another separation. But at the same time, the groups of parameters are not obtained as they were, but so as to reduce the prediction error. Clusterizers, as it were, try on each pixel to their mask, and at the same time, the pixel takes that clusterizer to which the pixel fits better.
Let's try to submit to the input double numbers, not superimposed on each other, but located side by side, here are the ones (this is one example, not two):

Now we see that every time, the separation is the same. That is, if there is a single, clearly the best way to separate the masks, then it will be selected.

Only one will be random, whether the first mask chooses the left figure or the right one.
I call the resulting masks meta-clusters. And the process of forming masks by meta-clustering. Why meta? Because clustering is not the input examples, but the inputs themselves.
The example is more complicated. Let's try to divide 25 parameters into 5 meta-clusters.
To do this, take five groups of five parameters, encoded with a unitary code.
That is, in each group one and only one unit in a random place. In each given example, always five units.
In the pictures below, each column is an input parameter, and each row is a meta-cluster mask. The clusters themselves are not shown.

100 parameters and 10 meta clusters:

Works! In some places, even a bit like the image of the matrix from the movie of the same name.
Using meta-clustering can drastically reduce the number of clusters.
For example, take ten groups of ten parameters, in each group one unit.
If we have one clusterizer (there are no meta-clusters), then we need 10 10 = 10000000000 clusters to get a zero error.
And if we have ten clusterizers, then we need only 10 * 10 = 100 clusters. This is similar to the decimal number system, no need to come up with notation for all possible numbers, you can do with ten numbers.
Meta clustering is very well parallelized. The most costly computations (comparison of the example with the cluster center) can be performed independently for each cluster. Notice, not for the clusteriser, but for the cluster.
How it works in the brain
Before that, I was talking only about dendrites, but neurons have axons. And they also learn. So, it seems that axons are masks of meta-clusters.
Add to the description of the work of the dendrites, above, another function.
Suppose that if a neuron spike occurs, all the dendrites somehow throw something into the synapse that indicates the concentration of the neurotransmitter in the dendrite. Not from an axon to a dendrite, but back. The concentration of this substance depends on the comparison error. Let, the smaller the error, the greater the amount of substance emitted. Well, the axon reacts to the amount of this substance and grows. And if the substance is small, which means a big mistake, then the axon gradually decreases.
And if axons are changed in this way from the very birth of the brain, then over time, they will only go to those groups of neurons where their spikes of these axons are needed (do not lead to big mistakes).
Example: let it be necessary to memorize human faces. Let each face be depicted using a megapixel image. Then for each person you need a neuron with a million dendrites, which is unrealistic. And now we divide all pixels into meta-clusters, such as eyes, nose, ears, and so on. Only ten such meta-clusters. Let there be ten clusters in each meta-cluster, ten variants of the nose, ten variants of the ears, and so on for everything. Now, to memorize a face, a neuron with ten dendrites is enough. This reduces the amount of memory (well, brain volume) by five orders of magnitude.
Conclusion
And now, if we assume that the brain consists of meta-clusters, we can try to consider from this point of view some concepts inherent in the living brain:
Clusters must be constantly trained, otherwise new data will not be processed correctly. For learning clusters in the brain, a balanced sample is needed. Let me clarify that if it is winter now, then the brain will learn only from winter examples, and the resulting clusters will gradually become relevant only to winter, and in the summer everything will be bad for this brain. What to do with it? It is necessary to submit periodically to all clusterizers not only new, but also old important examples (memories of both winter and summer). And so that these memories do not interfere with the current sensations, you need to temporarily disable the senses. In animals, this is called a dream .
Imagine the brain is seeing something small, GRAY, that is running. After meta-clustering, we have three active neurons in three meta-clusters. And thanks to the memory, the brain knows that it is delicious. Then, the brain sees something small, BLUE, that runs. But the brain does not know whether it is tasty or scary. It is enough to temporarily disable the meta-cluster where the colors are located, and only the small one that runs will remain. And the brain knows it is delicious. This is called an analogy .
Suppose the brain remembered something, and then changed the active neuron-cluster in some group to any other, while in the other meta-clusters there remains a real memory. And so, the brain has already presented something that has never seen before. And this is the imagination .
Thank you for your attention, the code is here .
Source: https://habr.com/ru/post/427407/
All Articles