How can LIGO see gravitational waves, if in GRT the light is stretched along with the space?

How can LIGO register gravitational waves if they stretch the light along with the space between the mirrors?

Image credit: www.ligo.caltech.edu

This question certainly arises when there is a conversation about the detection of gravitational waves (GW). Usually the argument is as follows: we know that there is a gravitational redshift , i.e. gravity stretches wavelengths. It is reasonable to assume that in LIGO the light will also stretch, and the wavelengths that we use as a “ruler” to measure the distance between the mirrors will stretch to the same extent as the distance itself. How, then, can an interferometer be used to measure gravitational waves?

Imagine the possible answers to it:
')

1. GW do not affect the light, so the question does not make sense.
2. GW stretch the wavelength of light, but very weakly, so that we do not notice.
3. It does not matter, the principle of detection is not sensitive to wavelength.
4. Detectors actually do not work.

1. Was there a boy?

To begin with, the detectors do work.


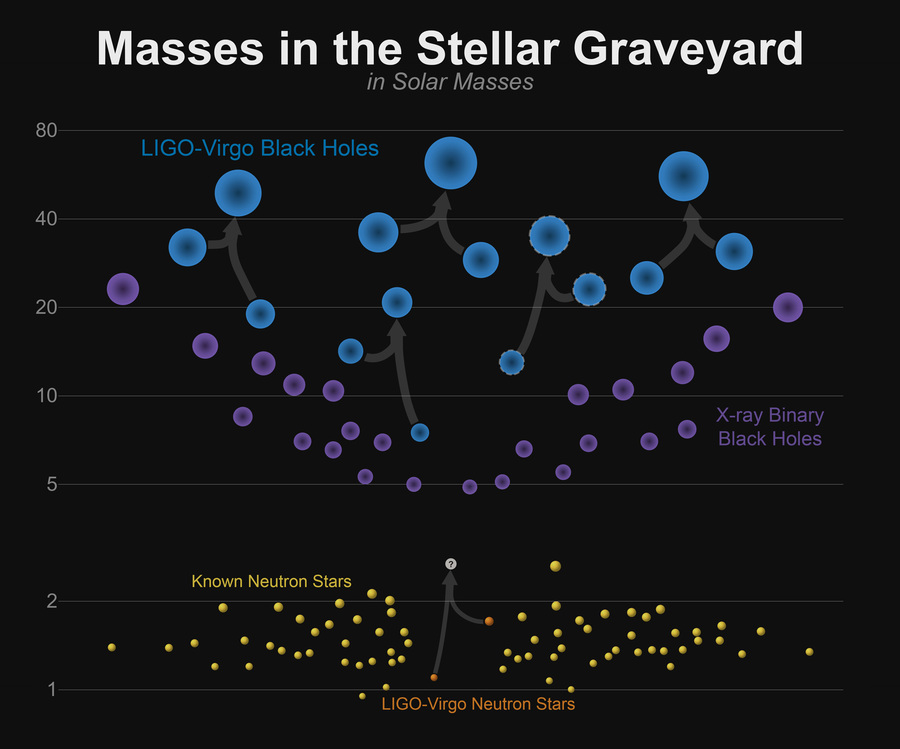
The cemetery of stars: the masses of neutron stars and black holes known to us, including the observations of LIGO. Image credit: www.ligo.caltech.edu


At the moment we have seen more than a dozen events with GW. The most convincing is the joint detection of HS and flashes of light from the fusion of neutron stars. In LIGO, they saw the GV, triangulated the area in the sky where they came from, and told the telescopes: “Look there!”. Those looked, and saw a flash of a kilon exactly where indicated from LIGO. So there is no doubt that it works. Let's see how exactly.

2. What is LIGO anyway?

The Virgo detector is a European detector, one of three detectors that have seen gravitational waves. Image credit: www.ligo.caltech.edu

A gravitational wave, arising from the merger of massive objects (for example, two black holes), propagates in space-time as a small perturbation of its curvature. This leads to the fact that the distances between objects change slightly when the wave passes through them (more precisely, the definition of the distance itself changes). In LIGO, the two arms of the Michelson interferometer with a length of 4 km change by ~ 10 ^-18 m, and the detector is able to catch this change. An important point: if the GW stretches one interferometer arm, the second arm will be compressed proportionally (ideally; this follows from the quadrupole nature of the GW and the presence of two polarizations in them).

On Habré there is already a good article about the LIGO device , so let's move on to the actual answer to the question posed at the beginning of the article.

3. The concept of measurement

An animation that demonstrates how detector works

To begin, consider an example that will help you understand the basic principle of the detector.
This detector works with continuous light - the laser constantly pumps resonators into LIGO with light, and photodiodes constantly record the presence / absence of a signal. But for example, let's simplify the scheme: suppose we have a photon source that simultaneously sends photons in two directions, they are reflected from the mirrors, and return to the photon detector (in our case, the beam divider), as shown in the illustration below.



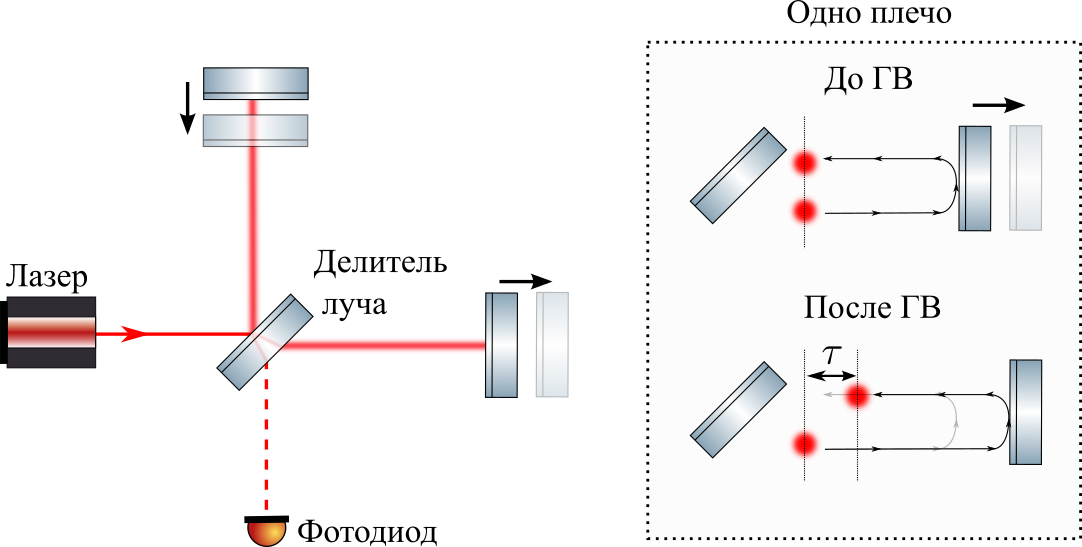
If two mirrors are at an equal distance from the photon source, two photons will return to the detector at the same time (as in the figure above). If GW stretches one shoulder to $$$x$ and compresses the other on $$$x$ , then one photon will come before another on $$$2 \ tau = 4x / c \ sim 4 \ times 10 ^ {- 18} / (3 * 10 ^ 8) \ sim 10 ^ {- 26}$ c, as in the picture above. This is very small, of course, and it would be impossible to measure directly, but we measure it a little differently. I just wanted to demonstrate the main message of this post:

The detector is not a ruler, but a clock

4. Detailed explanation

Let us now consider the Michelson interferometer, in which they shine with a continuous laser, the beam is divided equally in the beam divider, reflected from the final mirrors and, returning back to the beam divider, interferes.



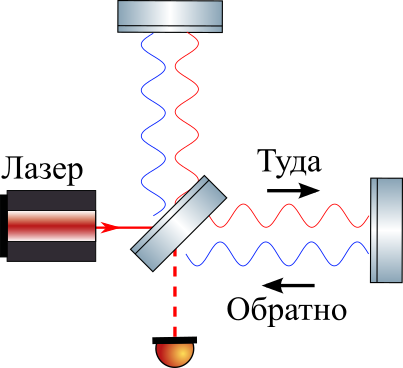
For simplicity, we assume that the GW is a "step" - instantly changes the metric by a small amount $$$h_0$ . By the words “change of metric” we mean that the definition of distance changes somewhat, i.e. all distances increase (or decrease) in $$$(1+ h_0 / 2)$ time. If we consider the distance between the beam divider and the end mirror $$$L$ , as the metric changes, it will increase by $$$\ Delta L$ , so that $$$h_0 = 2 \ Delta L / L$ .

Note: it is important that the representation of the HW “step” is only useful for viewing on the fingers, in reality it is necessary to consider the HW as a wave with a certain length.

Consider what happens to the light at that moment.


At the time of arrival of the GW, the wavelength of light is stretched relative to the initial wavelength (translucent curves). NB: the wavelength is shown comparable to that of the shoulder for clarity, in fact, the laser wavelength is about 1 micron, and the shoulder length is 4 km.

If the mirror before stretching was a node of the standing wave, it will remain in the same place after stretching, as shown in the picture above. Why? The theory of relativity requires this: since there is no dedicated independent system of rest, the node has no choice but to remain where it was relative to the surface of the mirror. That is, the wavelength increases in $$$(1 + h_0 / 2)$ times, as expected at the beginning of the article, by analogy with the gravitational redshift.

So it turns out that the light still stretched along with the detector, and we can not register the signal?

And yet we can!



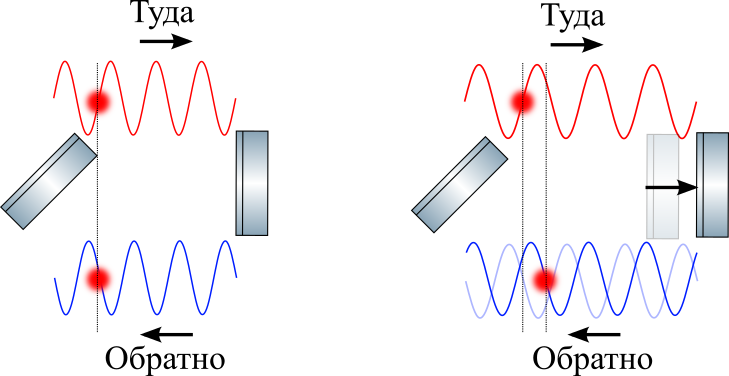
Let's show it in the picture above: let's trace the path of a particular node in a stretched wave on the way there and back, marking it with a circle. Despite stretching, light still travels at the speed of light. And this means that for the part of the wave that just entered the shoulder, it will take more time to overcome the way back and forth (recall point 3 from the article). That is, its phase upon arrival will change (as can be seen in the picture).

Moreover, the light continues to pump light with an unstretched wavelength.

The phase accumulated by the light on the way from the divider to the mirror and back depends on the natural frequency of the light. $$$\ omega _ {\ rm comp}$ observed on the beam splitter and time $$$\ tau _ {\ rm round-trip}$ :

$$

$$\ phi = \ omega _ {\ rm comp} \ tau _ {\ rm round-trip}$$

It can be shown (for example, here or here ) that if the wavelength of the GW is much greater than the length of the interferometer arm, the natural frequency remains almost unchanged. And the delay time will depend on the distance between the mirrors:

$$

$$\ tau _ {\ rm round-trip} \ approx \ frac {2 L} {c} (1+ \ frac {h_0} {2})$$

Accordingly, upon arrival at the beam splitter, the phase of the light will have a delay depending on the magnitude of the metric $$$h_0$ . In the other shoulder, everything will be the same to the sign before $$$h_0$ - because this shoulder will not stretch, but shrink. As a result, on the beam splitter, the phase difference between the two shoulders will be

$$

$$\ Delta \ phi = \ frac {2 \ omega L} {c} (1+ \ frac {h_0} {2}) - \ frac {2 \ omega L} {c} (1- \ frac {h_0} { 2}) = 2 \ pi \ frac {L} {\ lambda} h_0$$

From this equation, by the way, it is obvious why the detector has such a long shoulder - the longer the L is compared to the wavelength, the more sensitive the detector. Next-generation detectors, such as the Einstein Telescope or Cosmic Explorer , will be even longer - from 10 to 40 km.

I note that in reality HB is not a “step”, it is a wave with a wavelength much greater than the length of the shoulder, so during the time that one “node” of the light wave travels back and forth, its stretch can be neglected. Therefore, the first moment of "stretching" the light from viewing "on the fingers" is actually virtually absent.

So the conclusion. The correct answer to the question at the beginning of the article: both 2 and 3 - gravitational waves act on light a little differently than on the distance between the mirrors, but this does not matter, since in any case we measure not the wavelength, but the phase delay. In other words,

The gravitational-wave detector works like a clock, not like a ruler.

5. Conclusion

It is important to emphasize that the gravitational wave affects the wavelength of light differently than the distance between the mirrors. This is due primarily to the fact that the period of GW is much longer than the time it takes for the light to go back and forth. The shoulder of the interferometer continues to stretch over time, following the period of the GW, and the light all the time comes "new" from the laser.

In addition, in the real detector there are additional mirrors that create several resonators, which effectively increase the length of the shoulder. However, this does not affect the basic idea.

So we can really observe gravitational waves, and no conspiracy!

Image credit: www.ligo.caltech.edu

6. LIGO news

As a postscript, a little about what is happening in LIGO now. The second cycle of O2 observations brought not only the observation of neutron star fusion and the first joint observation of GW by three detectors , including Virgo, but also many other events. In the very near future, the results of data analysis will be published, and the data itself will become open and available for analysis.

LIGO is now completing numerous updates, including the installation of compressed light and a more powerful laser, which will increase the sensitivity of the detector several times and allow you to observe much more events (with a good deal - on an event per week).

At the beginning of next year, a new O3 observation cycle will begin.