Build functions in the console. Part 1

Most probably have a reasonable question: why?



From a pragmatic point of view, there is no need) You can always use a conventional Tungsten, and if you need to do this in python, then use special modules that are not so difficult to master.

')

But if suddenly you were given such a task or you just love programming very much, like me, then you will have fascinating - and sometimes not very much - hours of writing a program and debugging it)



When writing this masterpiece, we really need step-by-step debugging, so please download PyCharm, VS or something else with this feature. For the construction of tables, the absence of this function is not so critical yet, but for plotting a graph ...



So, what will be my program. At the input it will take three values: the beginning and the end of the segment where we want to see our function and the step with which we will move. Next, we will draw a table of function values ​​at each point of the range of values ​​specified by the input data. Well, then we will draw the graph of the function itself with a moving y axis.



So let's go



To begin, I will declare several functions, the values ​​of which we will consider. Specially take pretty simple

from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x))) 

Now we have three functions, two of which have a break point. From the math module, in which all mathematical buns are stored (including cosines, arctangents and other trigonometry), we import sqrt, that is, the square root. We need it in order to read the function y3.



After that, we need to consider the range of the function on X and the step with which we will go through this range. For this I will use the map.



As a first parameter, this function accepts some function that somehow converts the data we need, and the second argument is some kind of data sheet that we need to process.

 from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split()) 

We read three values ​​entered with a space, divide them into elements by spaces (using the split method, which, when called without parameters, will automatically divide the string you specify by spaces). The data entered using input () will by default be of type str, that is, a string, so we will not have any errors here.



Since the range bounding numbers can be fractional, we convert each element of the resulting array into a real number using the float function.



I note that the variables are declared without specifying the data type. It is determined automatically (the data type of the value you are trying to assign to a variable), or using the functions str, int, float, etc. they are set manually by applying these functions to the values. The same variable can have a different data type during the whole program - for this it is enough to assign a new value to it with a different data type.



For example,

 auxiliary_variable = "" #   str auxiliary_variable = 2 #   int auxiliary_variable = 9.218 #   float 

Let's return to our program. We need to check if the entered data is correct.



The program should print that the entered data is incorrect if:

• step equals 0
• The entered lower bound of the range is greater than the upper, and the step is positive (that is, we have an arithmetic progression of the form xn = from_x + pace_x * (n - 1) , in which from_x> to_x . Since pace_x> 0, then this progression will be increasing and we never get to to_x )
• the entered lower bound of the range is less than the upper one, and the step is negative (similar reasoning)
• graphs consisting of one point are not informative, so the segment on which we build the function must contain at least two values

We formulate these conditions in the code. Obviously, the first item is easy to set up. The second and third can be combined into one, if you notice that the sign of the difference between the first (from_x) and the last (to_x) must match the step sign. Well, the fourth point is also not so complicated: the modulus of the difference between the first and the last value should be no less than the modulus of the step.



Because of the module, we may have a situation in which the signs of the difference and the step will not coincide, but the second condition cuts off these cases, so the condition is correct.



As a result, these three conditions will look like this:

 if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x): #-  else: print("Incorrect input") 

Let's go directly to the table. For ease of debugging, I will create several variables with talking names that are responsible for the accuracy of numbers, the number of spaces before the number, the number of spaces after the number, etc.

 dials_precision = "%10.6g" #   spaces_in_the_title = int((int(dials_precision[1:3])) / 2) length_of_table_lower_bound = (int(dials_precision[1:3]) + 2) * 4 + 5 delimiter = ' ' is_sequence_decreasing = to_x - from_x < 0 min_y1_value, max_y1_value, x_copy = y1(from_x), y1(from_x), from_x negative_value_exists = False 

So what is going on here?

 dials_precision = "%10.6g" #   

In this line I set the accuracy of the number. Maximum 10 characters for the whole number and 6 characters for the fractional part. If we have too large a value for this range, then all sorts of e-15 or something similar will appear.

 spaces_in_the_title = int((int(dials_precision[1:3])) / 2) 

dials_precision is a string, so we can take a slice of this string, that is, some kind of substring. In this case, we need to get the number 10, so we take the characters under the 1 and 2 indices, this substring is reduced to an integer data type, divided by two and rounded down.



We need this variable to ensure that the captions in the table heading are aligned to the center of the cell.

 length_of_table_lower_bound = (int(dials_precision[1:3]) + 2) * 4 + 5 

as the name implies, this variable is responsible for the length of the lower bounds of the cells of the table of function values. The total number in us is 10 positions, so the column cannot be less than 10 wide. When we have numbers with the format e-15 (described above), the value takes 11-12 positions. Therefore, to 10 we add another two.



4 is responsible for the number of columns (x, y1, y2, y3), and 5 for the number of characters bounding a cell in a row.



The remaining variables seem to be intuitive, so go to the print labels

 print("|" + (spaces_in_the_title + 1) * delimiter + 'x' + spaces_in_the_title * delimiter + '|' + spaces_in_the_title * delimiter + "y1" +\ spaces_in_the_title* delimiter\ + '|' + spaces_in_the_title * delimiter + 'y2'\ + spaces_in_the_title * delimiter + '|' +\ spaces_in_the_title * delimiter\ + "y3" + spaces_in_the_title * delimiter + "|\n"\ + length_of_table_lower_bound * '-') 

If you combine all the code that we have already written, then we will see this in the console:







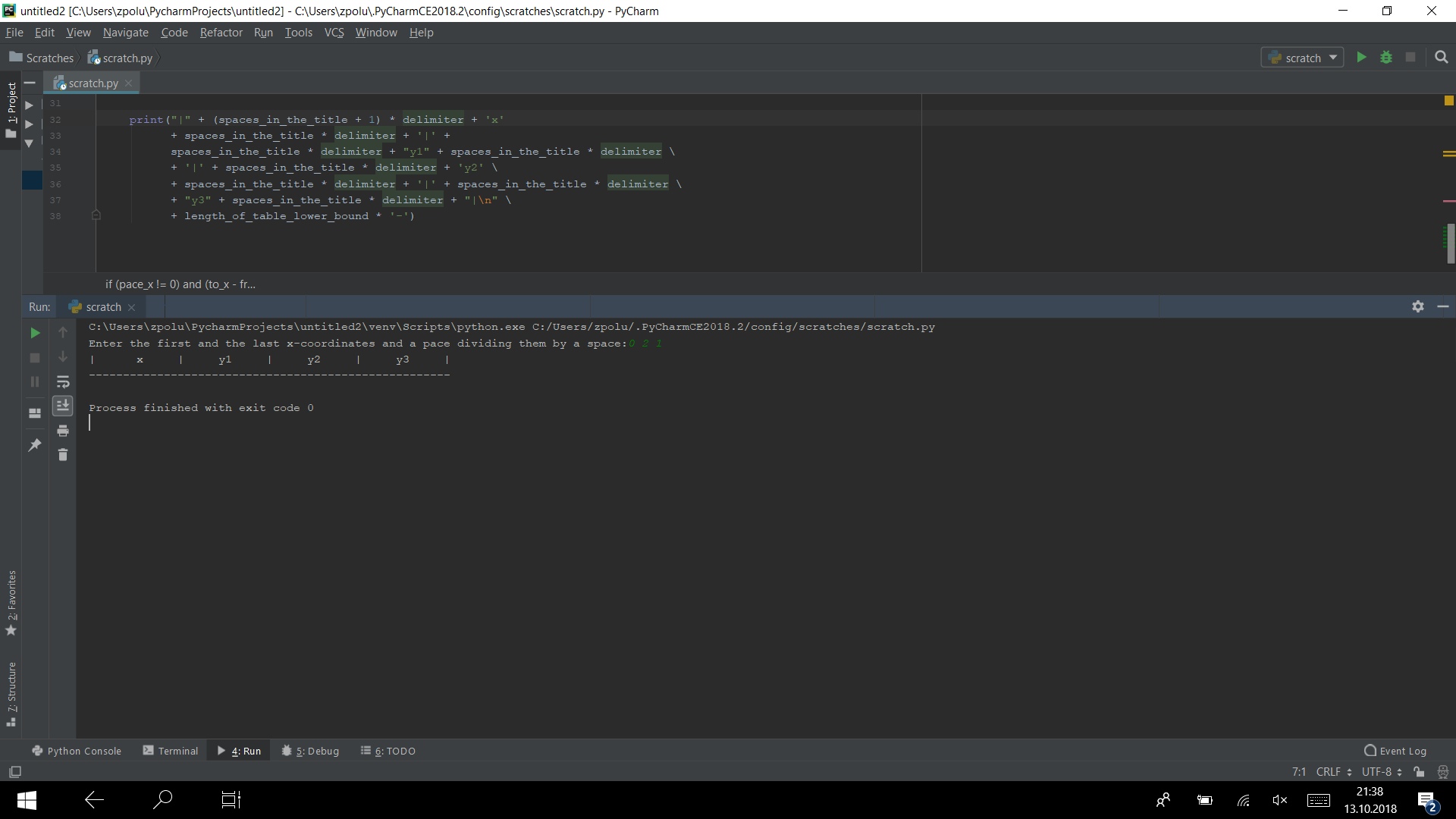
Now we need to print the values ​​themselves. For this you need a cycle. Since the entered data can be fractional, the use of range will not work, so I will use the normal loop.



Since we can have both a decreasing sequence of X's and an increasing one, the cycle conditions should be set so that both of these options are taken into account. We have a previously created variable that stores the answer about the nature of the sequence in the form of 0 or 1. Therefore, it suffices to consider two cases and choose the appropriate condition for each

 while(is_sequence_decreasing and x_copy >= to_x) or\ (not is_sequence_decreasing and x_copy <= to_x): 

Since for the graph we need the minimum and maximum of the graph y1, which we will draw, we introduce special variables that will be responsible for the min and max

 y1_cur_value = y1(x_copy) min_y1_value = (min_y1_value > y1_cur_value) * y1_cur_value + \ (min_y1_value <= y1_cur_value) * min_y1_value max_y1_value = (max_y1_value < y1_cur_value) * y1_cur_value + \ (max_y1_value >= y1_cur_value) * max_y1_value negative_value_exists += y1_cur_value < 0 

the construction essentially repeats the if: ... else: ... construction only through Boolean inequalities. y1_cur_value stores the current value of the function. I created a variable in order not to constantly call a function when its value is needed at a point.

We also need the presence of negative values ​​for plotting.







Now directly print values. I want everything to be beautiful and centered in each of the cells, so I have to manually process each value to check the length of the number and select the number of gaps depending on it to align the value.



Note

Literally align the number in the center will not work. The variable responsible for precision is the parameter g. He says that a number is reserved for a number of positions under the numbers (in our case, 10 by default). If 10 digits are not dialed, the blank positions will be located to the left of the filled positions. Therefore, we can align in the center only a line of 10 positions.

 aux_x = dials_precision % x_copy aux = len(aux_x) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_x) == int(dials_precision[1:3]) + 1 print('|' + delimiter * aux + aux_x + delimiter * (aux - aux_2) + '|', end='') 

aux_x is a string that has already been displayed with a given precision. Now we need to check the length of the number and select the required number of spaces. Since more than one space from each side is not needed, the bool variables are perfect as a keeper of the number of these spaces. aux_2 catches the case when the length of a number is 11.



We also do for the values ​​of three functions

  aux_y1 = dials_precision % y1_cur_value aux = len(aux_y1) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y1) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y1 + delimiter * (aux - aux_2) + '|', end='') if (x_copy != 0): aux_y2 = dials_precision % y2(x_copy) aux = len(aux_y2) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y2) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y2 + delimiter * (aux - aux_2) + '|', end='') aux_y3 = dials_precision % y3(x_copy) aux = len(aux_y3) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y3) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y3 + delimiter * (aux - aux_2) + \ "|\n" + length_of_table_lower_bound * '-') else: print((spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + '|' \ + (spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + "|\n" \ + length_of_table_lower_bound * '-') x_copy += pace_x 

As I said at the very beginning, the second and third functions have break points - both functions do not exist at x = 0. Therefore, we also need to catch these cases.



Well, do not forget to increase the current value of X, so that we do not get an infinite loop.



Let's collect all the code in one program and run it, for example, on test -1.2 3.6 0.3

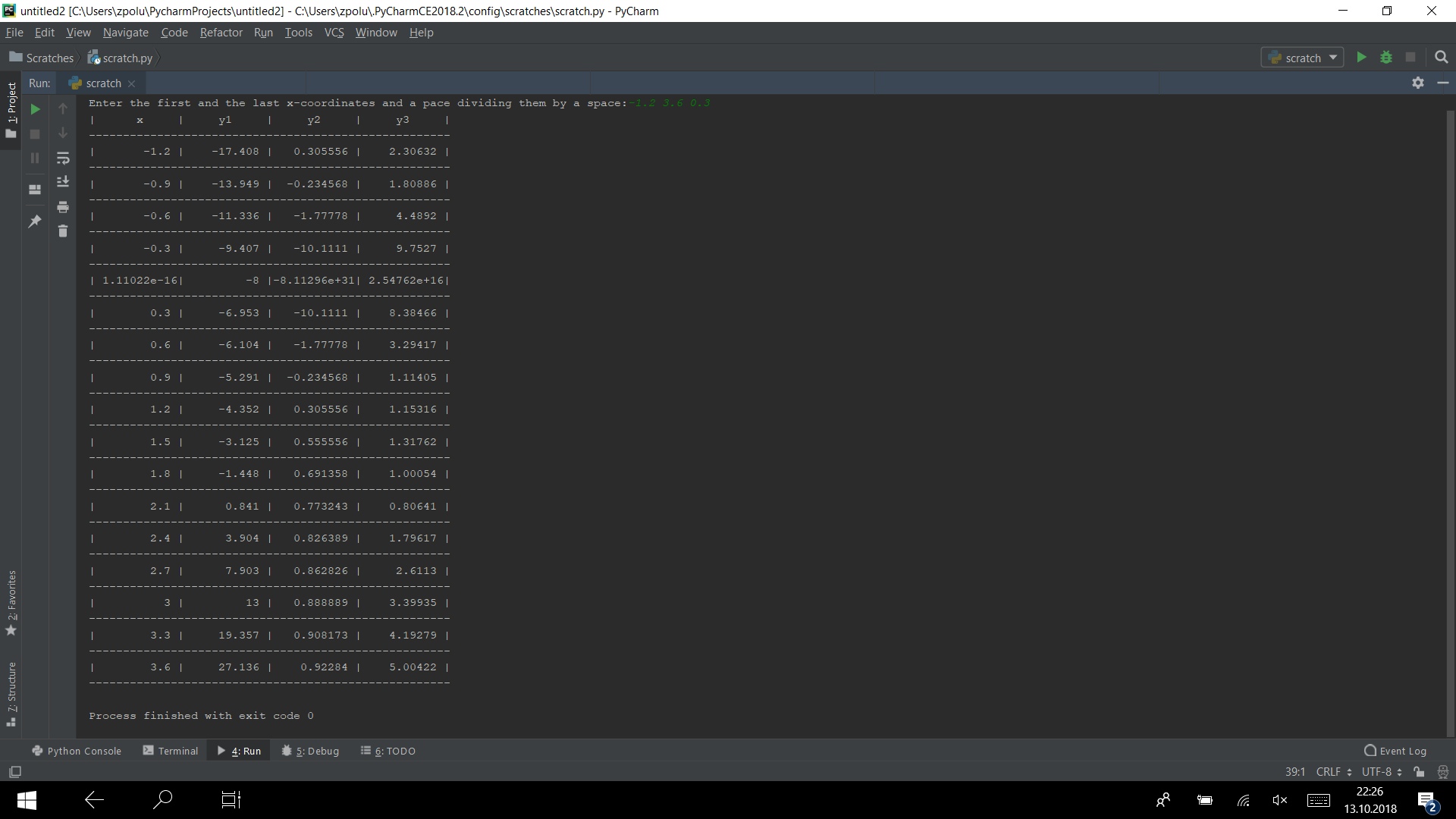
 from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x))) from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split()) if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x): dials_precision = "%10.6g" #   spaces_in_the_title = int((int(dials_precision[1:3])) / 2) length_of_table_lower_bound = (int(dials_precision[1:3]) + 2) * 4 + 5 delimiter = ' ' is_sequence_decreasing = to_x - from_x < 0 min_y1_value, max_y1_value, x_copy = y1(from_x), y1(from_x), from_x negative_value_exists = False print("|" + (spaces_in_the_title + 1) * delimiter + 'x' + spaces_in_the_title * delimiter + '|' + spaces_in_the_title * delimiter + "y1" + spaces_in_the_title * delimiter \ + '|' + spaces_in_the_title * delimiter + 'y2' \ + spaces_in_the_title * delimiter + '|' + spaces_in_the_title * delimiter \ + "y3" + spaces_in_the_title * delimiter + "|\n" \ + length_of_table_lower_bound * '-') while (is_sequence_decreasing and x_copy >= to_x) or \ (not is_sequence_decreasing and x_copy <= to_x): y1_cur_value = y1(x_copy) min_y1_value = (min_y1_value > y1_cur_value) * y1_cur_value + \ (min_y1_value <= y1_cur_value) * min_y1_value max_y1_value = (max_y1_value < y1_cur_value) * y1_cur_value + \ (max_y1_value >= y1_cur_value) * max_y1_value negative_value_exists += y1_cur_value < 0 aux_x = dials_precision % x_copy aux = len(aux_x) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_x) == int(dials_precision[1:3]) + 1 print('|' + delimiter * aux + aux_x + delimiter * (aux - aux_2) + '|', end='') aux_y1 = dials_precision % y1_cur_value aux = len(aux_y1) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y1) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y1 + delimiter * (aux - aux_2) + '|', end='') if (x_copy != 0): aux_y2 = dials_precision % y2(x_copy) aux = len(aux_y2) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y2) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y2 + delimiter * (aux - aux_2) + '|', end='') aux_y3 = dials_precision % y3(x_copy) aux = len(aux_y3) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y3) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y3 + delimiter * (aux - aux_2) + \ "|\n" + length_of_table_lower_bound * '-') else: print((spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + '|' \ + (spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + "|\n" \ + length_of_table_lower_bound * '-') x_copy += pace_x else: print("Incorrect input") 

In the second part of this creation, we will build graphics







To be continued ...