Prehistory

The reason for this publication is an ambiguous article on the principle of least action (PND) , published on the resource a few days ago. It is ambiguous because its author in a popular form is trying to convey to the reader one of the fundamental principles of the mathematical description of nature, and this is partly possible for him. If it were not for one thing, lurking at the end of the publication. Under the spoiler is a full quote of this passage.


So what, in my opinion, is the problem?

The problem is that the author, citing this example, made a number of fundamental errors. It is aggravated by the fact that the planned second part, according to the author, will be based on these errors. Guided by the principle of filling the resource with reliable information, I have to speak in more detail about my position on this issue, and the format of comments for this is too small.

This article will talk about how mechanics are built on the basis of the HDPE, and will try to explain to the reader that the problem posed by the author of the cited publication is missing.

1. Definition of Hamilton action. Principle of least action

Hamilton action is called functional

$$

$$S = \ int \ limits_ {t_1} ^ {t_2} \, L \ left (\ mathbf q (t), \ dot {\ mathbf q} (t) \ right) \, dt$$

Where

$$

$$L \ left (\ mathbf q (t), \ dot {\ mathbf q} (t) \ right) = T \ left (\ mathbf q (t), \ dot {\ mathbf q} (t) \ right) - \ Pi (\ mathbf q)$$

- Lagrange function, for some mechanical system, in which (omitting the arguments in the following) T is the kinetic energy of the system; P - its potential energy; q (t) is the vector of generalized coordinates of this system, which is a function of time. at the same time, it is assumed that the times t ₁ and t ₂ are fixed.

Why functionality, but not function? Because a function, by definition, is a rule according to which one number from the domain (function argument) is assigned a different number from the domain. The functional differs in that the quality of its argument is not a number, but an entire function. In this case, it is the law of motion of the mechanical system q (t), determined at least over the time interval between t ₁ and t ₂ .

The perennial (and this is put it mildly!) Works of mechanical scientists (including the astounding Leonard Euler) made it possible to formulate

The principle of least action:

Mechanical system for which the Lagrange function is set $$$L \ left (\ mathbf q (t), \ dot {\ mathbf q} (t) \ right)$ , moves in such a way that the law of its movement q (t) delivers a minimum to the functional

$$

$$S = \ int \ limits_ {t_1} ^ {t_2} \, L \ left (\ mathbf q (t), \ dot {\ mathbf q} (t) \ right) \, dt \ to \ min$$

called the Hamilton action.

Already from the very definition of PND, it follows that this principle leads to equations of motion only for a limited class of mechanical systems. For what? And let's see.

2. Limits of applicability of the principle of least action. Some definitions for the smallest

As follows from the definition, again, the Lagrange function, PND allows to obtain the equations of motion for mechanical systems, the force for which is determined solely by the potential energy. In order to figure out which systems we are talking about, we will give a few definitions, which, to save the volume of the article, I place under the spoiler

3. The concept of variations of generalized coordinates. Statement of the variational problem

So, we now consider a mechanical system moving under the action of potential forces, the position of which is uniquely given by the vector of generalized coordinates

$$

$$\ mathbf q = \ left [q_1, \, q_2, \, \ dots, \, q_s \ right] ^ T \ quad (4)$$

where s is the number of degrees of freedom of the given system.

Actual, but not yet known to us , the law of motion of this system is determined by the dependence of the generalized coordinates (4) on time. Consider one of the generalized coordinates. $$$q_i = q_i (t)$ assuming similar reasoning for all other coordinates.


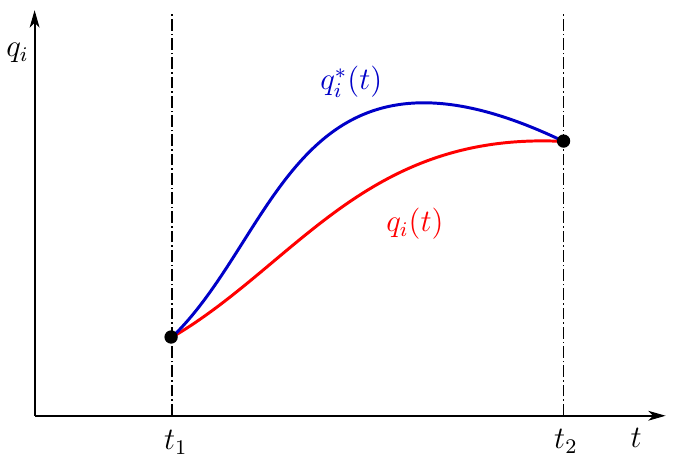
Figure 1. Real and detour movement of a mechanical system

In the figure, the dependence $$$q_i (t)$ depicted by a red curve. Choose two arbitrary fixed moments of time t ₁ and t ₂ , setting t ₂ > t ₁ . System position $$$\ mathbf q_1 = \ mathbf q (t_1)$ agree to call the initial position of the system, and $$$\ mathbf q_2 = \ mathbf q (t_2)$ - the final position of the system.

However, I once again insist that the following text be read carefully! Despite the fact that we set the initial and final position of the system, neither the first position nor the second is known to us in advance! As well as the unknown law of the movement of the system! These provisions are considered precisely as the initial and final position, regardless of specific values.

Further we assume that from the initial position to the final system can come in different ways, that is, the dependence $$$\ mathbf q = \ mathbf q (t)$ can be any kinematically possible. The real motion of the system will exist in a single variant (red curve), the remaining kinematically possible variants will be called circumferential motions. $$$\ mathbf q ^ {*} = \ mathbf q ^ {*} (t)$ (blue curve in the picture). Difference between real and roundabout traffic

$$

$$\ delta q_i (t) = q ^ {*} _ i (t) - q_i (t), \ quad \ forall i = \ overline {1, s} \ quad (5)$$

will be called isochronous variations of generalized coordinates

In this context, variations (5) should be understood as infinitesimal functions expressing the deviation of a roundabout motion from the real one. The small “delta” for the designation was not chosen randomly and underlines the fundamental difference between the variation and the differential of the function. The differential is the main linear part of the function increment, caused by the argument increment. In the case of variation, a change in the value of a function with a constant value of the argument is caused by a change in the type of the function itself! We do not vary the argument, in the role of which time plays, therefore the variation is called isochronous. We vary the rule according to which each value of time corresponds to a certain value of generalized coordinates!

In fact, we vary the law of motion according to which the system moves from the initial state to the final state. The initial and final states are determined by the actual law of motion, but I emphasize once again - we don’t know their specific values ​​and can be any kinematically possible, we just assume that they exist and the system is guaranteed to move from one position to another! In the initial and final position of the system, we do not vary the law of motion; therefore, the variations of the generalized coordinates in the initial and final position are zero.

$$

$$\ delta q_i (t_1) = \ delta q_i (t_2) = 0, \ quad \ forall i = \ overline {1, s} \ quad (6)$$

Based on the principle of least action, the actual movement of the system should be such as to deliver a minimum of action functionality. Variation of coordinates causes a change in the action functional. A necessary condition for the achievement of an extremal value by a functional is that its variation is zero.

$$

$$\ delta S = \ delta \ int \ limits_ {t_1} ^ {t2} \, L (q_1, \ dots, q_s, \, \ dot q_1, \ dots, \ dot q_s) \, dt = 0 \ quad ( 7)$$

4. The solution of the variational problem. Lagrange equations of the 2nd kind

We solve the variational problem we have set, for which we calculate the total variation of the action functional and equate it to zero

$$

$$\ begin {align} \ delta S = & \ int \ limits_ {t_1} ^ {t2} \, L (q_1 + \ delta q_1, \ dots, q_s + \ delta q_s, \, \ dot q_1 + \ delta \ dot q_1, \ dots, \ dot q_s + \ delta \ dot q_s) \, dt - \\ & - \ int \ limits_ {t_1} ^ {t2} \, L (q_1, \ dots, q_s, \, \ dot q_1, \ dots, \ dot q_s) \, dt = 0 \ end {align}$$

We will drive everything under one integral, and since for variations all operations on infinitely small quantities are valid, we will transform this crocodile to the form

$$

$$\ int \ limits_ {t_1} ^ {t_2} \ left [\ sum \ limits_ {i = 1} ^ s \ frac {\ partial L} {\ partial q_i} \ delta q_i + \ sum \ limits_ {i = 1 } ^ s \ frac {\ partial L} {\ partial \ dot q_i} \ delta \ dot q_i \ right] \, dt = 0 \ quad (8)$$

Based on the definition of generalized speed

$$

$$\ delta \ dot q_i = \ frac {d (\ delta q_i)} {dt}$$

Then the expression (8) is converted to

$$

$$\ int \ limits_ {t_1} ^ {t_2} \ left [\ sum \ limits_ {i = 1} ^ s \ frac {\ partial L} {\ partial q_i} \ delta q_i \, dt + \ sum \ limits_ { i = 1} ^ s \ frac {\ partial L} {\ partial \ dot q_i} d (\ delta q_i) \ right] = 0$$

The second term is integrated in parts

$$

$$\ sum \ limits_ {i = 1} ^ s \ frac {\ partial L} {\ partial \ dot q_i} \ delta q_i | _ {t_1} ^ {t_2} + \ int \ limits_ {t_1} ^ {t_2} \ left [\ sum \ limits_ {i = 1} ^ s \ frac {\ partial L} {\ partial q_i} \ delta q_i - \ sum \ limits_ {i = 1} ^ s \ frac {d} {dt} \ left (\ frac {\ partial L} {\ partial \ dot q_i} \ right) \ delta q_i \ right] \, dt = 0 \ quad (10)$$

Based on condition (7), we have

$$

$$\ sum \ limits_ {i = 1} ^ s \ frac {\ partial L} {\ partial \ dot q_i} \ delta q_i | _ {t_1} ^ {t_2} = 0$$

then, we get the equation

$$

$$\ int \ limits_ {t_1} ^ {t_2} \ left [\ sum \ limits_ {i = 1} ^ s \ left (\ frac {\ partial L} {\ partial q_i} - \ frac {d} {dt} \ left (\ frac {\ partial L} {\ partial \ dot q_i} \ right) \ right) \, \ delta q_i \ right] \, dt = 0$$

With arbitrary limits of integration, the equality to zero of a certain integral is ensured by the equality to zero of the integrand

$$

$$\ sum \ limits_ {i = 1} ^ s \ left [\ frac {\ partial L} {\ partial q_i} - \ frac {d} {dt} \ left (\ frac {\ partial L} {\ partial \ dot q_i} \ right) \ right] \, \ delta q_i = 0 \ quad (11)$$

Taking into account the fact that the variations of the generalized coordinates are independent, (11) is valid only if all coefficients are zero for variations, that is,

$$

$$\ frac {\ partial L} {\ partial q_i} - \ frac {d} {dt} \ left (\ frac {\ partial L} {\ partial \ dot q_i} \ right) = 0, \ quad \ forall i = \ overline {1, s}$$

No one bothers us to multiply each of the equations by (-1) and get a more familiar record

$$

$$\ frac {d} {dt} \ left (\ frac {\ partial L} {\ partial \ dot q_i} \ right) - \ frac {\ partial L} {\ partial q_i} = 0, \ quad \ forall i = \ overline {1, s} \ quad (12)$$

Equations (12) are the solution to the problem . And here at this point once again attention - the solution of a variational problem on the principle of least action, is not a function that delivers a minimum to the Hamilton action, but a system of differential equations that can be solved by solving such a function . In this case, this is the second-kind Lagrange differential equation written through the Lagrange function, that is, in the formulation for conservative mechanical systems.

And that's it, the principle of the smallest action ends , and the theory of ordinary differential equations begins, which, in particular, says that the solution of equation (12) is a vector function of the form

$$

$$\ mathbf q = \ mathbf q (t, C_1, C_2, \ dots, C_ {2s})$$

where C ₁ , ..., C _2s are arbitrary integration constants.

In this way

PND - a fundamental principle that allows to obtain the equations of motion of a system for which the Lagrange function is defined

Point! In the problems of analytical mechanics, the above calculations no longer need to be done, it is enough to use their result (12). The function that satisfies equation (12) is the law of motion of the system that satisfies the MHP.

5. The challenge with the ball and the wall

Now let us return to the problem with which everything began - about the one-dimensional motion of a ball near an absolutely elastic wall. Of course, for this problem one can obtain differential equations of motion. Since these are differential equations of motion, then any, I emphasize this, any solution to them delivers a minimum to the action functional, which means the HDPE is executed! The general solution of the equations of motion of a ball can be represented as a so-called phase portrait of the mechanical system under consideration. Here is the phase portrait


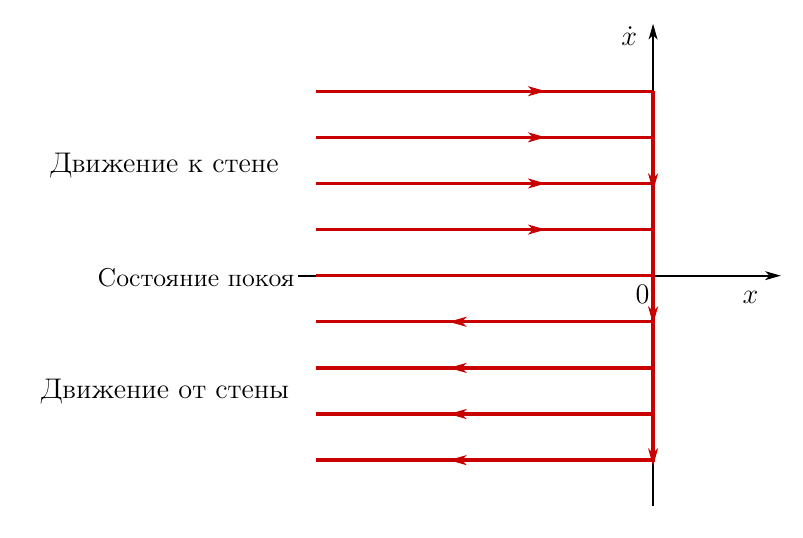
Figure 2. Phase portrait of the system in the problem with the ball

The coordinate of the ball is plotted along the horizontal axis, and the velocity projection onto the x axis is plotted along the vertical axis. It may seem strange, but this drawing reflects all possible phase trajectories of the ball, with any initial, or if you so wish, boundary conditions. In fact, there are infinitely many parallel lines on the graph; the drawing shows some of them and the direction of movement along the phase trajectory.

This is a general solution of the ball motion equation. Each of these phase trajectories provides a minimum of action functionality, which directly follows from the calculations performed above.

What does the author of the task? He says: the ball is at rest, and for the time from t _A to t _{B the} action is zero. If the ball is pushed to the wall, then for the same period of time the action will be longer, since the ball has a nonzero and constant kinetic energy. But why does the ball move to the wall, because at rest the action will be less? So PND is experiencing problems and does not work! But we will definitely solve it in the next article.

What the author says is nonsense. Why? Yes, because it compares the actions on different branches of the same real phase trajectory! Meanwhile, when using PND, the action is compared on the real trajectory and on the set of roundabout trajectories. That is, the action on the real trajectory is compared with the action on those trajectories that are not in nature, and never will be!

Unclear? I will explain even more intelligibly. Consider the state of rest. It is described by a branch of the phase portrait that coincides with the abscissa axis. Coordinate does not change over time. This is a real movement. And what kind of movement will be roundabout. Any other kinematically possible. For example, small oscillations of a ball near the rest position considered by us. The task allows the ball to oscillate along the x axis? Allows, then this movement is kinematically possible and can be considered as one of their devious

Why does the ball rest? Yes, because the action at rest, calculated on a fixed period of time from t _A to t _B , will be less than the action, with small fluctuations on the same period of time. It means that nature prefers rest to oscillations and any other “stirring” of the ball. In full compliance with the IPA.

Suppose we pushed the ball toward the wall. Suppose we pushed it as the author wants, at a speed selected from the boundary conditions, so that at time t _{B the} ball is in the same position from which it started. The ball, at a constant speed, reaches the wall, bounces elastically and returns to the initial position at time t _B , again at a constant speed. Ok, this is a real move. What movement will be one of the roundabouts? For example, if the ball moves to the wall and away from the wall at a rate varying with time. Such a movement is possible kinematically? Maybe. Why doesn't the speed of the ball change? Yes, because the effect on such a phase trajectory will have a minimum value, in comparison with any other option, where the speed depends on time.

That's all. Nothing such magic happens here. HDPE works without any problems.

Conclusions and wishes

PND is a fundamental law of nature. In particular, laws of mechanics, for example, differential equations of motion (12), follow from it. PND tells us that nature is structured in such a way that the equation of motion of a conservative mechanical system looks exactly like expression (12) and in no other way. More from him and is not required.

No need to invent problems where there are none.