MIT course "Computer Systems Security". Lecture 10: "Symbolic execution", part 2

Massachusetts Institute of Technology. Lecture course # 6.858. "Security of computer systems". Nikolai Zeldovich, James Mykens. year 2014

Computer Systems Security is a course on the development and implementation of secure computer systems. Lectures cover threat models, attacks that compromise security, and security methods based on the latest scientific work. Topics include operating system (OS) security, capabilities, information flow control, language security, network protocols, hardware protection and security in web applications.

Lecture 1: "Introduction: threat models" Part 1 / Part 2 / Part 3
Lecture 2: "Control of hacker attacks" Part 1 / Part 2 / Part 3
Lecture 3: "Buffer overflow: exploits and protection" Part 1 / Part 2 / Part 3
Lecture 4: "Separation of privileges" Part 1 / Part 2 / Part 3
Lecture 5: "Where Security Errors Come From" Part 1 / Part 2
Lecture 6: "Opportunities" Part 1 / Part 2 / Part 3
Lecture 7: "Sandbox Native Client" Part 1 / Part 2 / Part 3
Lecture 8: "Model of network security" Part 1 / Part 2 / Part 3
Lecture 9: "Web Application Security" Part 1 / Part 2 / Part 3
Lecture 10: "Symbolic execution" Part 1 / Part 2 / Part 3

Audience: it seems you didn’t talk about how bits are used to store an integer int.
')
Professor: this is a very good question. And this is really related to how you define your limitations, right? Therefore, if you look at our simple example from the very beginning, you will see that we assumed the presence of integers that we studied in elementary school. At the same time, we completely decided to ignore overflow errors. If you care about overflow errors, and it is important for you that there are no such errors, using mathematically whole numbers will not fix the problem.



What you need is to present these values ​​not as integers, but as bit vectors. When you present them as bit vectors, you should use a broader view of things. Here we return to the SMT solvers. The aspect of modular theory is that the solver itself is expandable with the help of various theories.

The most popular theories are theories of bit vectors of fixed length. This means that if you interpret your formulas in the theory of fixed-length bit vectors, you have to pre-set the length of the bit vectors. That is, you must explicitly indicate that this will be used for bit vectors with a length of 32 bits, or 8 bits, or 64 bits.



There is another theory called the TOA array theory. And we will talk a little more about it. Unlike the theory of bit vectors, which is intended for things of fixed length, the theory of arrays is intended for collections whose size is a priori unknown.

Now, in practice, no one uses the theory of arrays, for example, to model integers, because it is too expensive. Much more expensive to talk about the problem when you do not know its boundaries. Therefore, as a rule, people use the theory of fixed length of bit vectors when reasoning about integers or even symbols.

Another very common theory is the theory of real integer arithmetic, and in particular linear integer arithmetic.



People love this theory very much, because it provides effective reasoning, but it’s not very good when you talk about programs, because here you really care about the problems of overflow. But this theory is widely used for many things.

Another theory that is often used is the theory of uninterpreted functions. What does this theory mean?



It means that you have some formula. In this formula, you know that you are calling a function, but you don’t know anything about this function except for the fact that if you insert some input data into it, you will get the same output data.

It turns out that this is very useful when talking about things like using floating point code, modeling, sines, cosines, square roots. Detailed reasoning about such things can be very time consuming and expensive. But using this theory allows you to say: “Listen, I really don't care what the sine function does. I don't care what exactly it will give out at the exit. I just need to know that if I call the sine function in different places in the program with specific inputs, I will get data of the same kind on the output. This is quite enough for me to talk about my program. ”

And so the most common operations in the analysis of real systems are bit vectors that work with integers, logs and pointers. In fact, pointers are often represented as integers, because sometimes you don't set bit vectors on pointers. But sometimes you have to do it, and then you can no longer use whole numbers.

So, we looked at what the SMT solver can do for you. How does it really work? What is inside them that makes them work?

In fact, SMT solvers rely on our ability to solve the satisfiability problems of the SAT boolean formulas, on the ability to deal with problems related only to purely boolean constraints and boolean variables, and tell us whether you will ensure the execution of the program values ​​assigned to these boolean variables or not .

This is something that many, many years have taught undergraduates, saying that this is actually an NP-complete task, and in cases where something comes down to the SAT, you should not do that. But it turns out that we actually have very good SAT solvers.

So, I will tell you the basic idea of ​​how the SAT solvers work. It lies in the fact that you take all your constraints on Boolean variables and put them in a database. You may not be able to see the small letters on the screen, but that's all I can do.



I will comment and tell about it in the course of the action, and later I will publish the slides so that you can see what is written there.

So, here in the SAT task we have all these variables representing Boolean unknowns, right? We want to know if it is possible for both X to be true (X = TRUE), and Y to be true, and Z to be true. These are our unknowns. Moreover, all restrictions are in a normal conjunctive form. This means that all our limitations are in the form of either X1 = true, or X2 = true, or X3 = true.



In this form, we have all our limitations, which say that either X1 is true, or X2 is false, or X3 is false. You probably remember from discrete mathematics that any Boolean formula can be represented in a normal connective form. This means that any representation that you use to represent Boolean formulas can be converted to this format very easily.

So, we have a database with a lot of limitations of this form. The SAT solver will select one of these variables randomly, supposing it to be X1. And he will say: “why not set X1 to true? I don’t know anything about these restrictions, so I can assume that this is true. ” And then it will happen that you will have restrictions, which, for example, claim that either X1 is false, or X7 is true.

So, if you know that X1 is true and you know that either X1 is false or X7 is true, what do you know about X7?

Audience: it must be true!

Professor: yes, it must be true. Because otherwise this restriction will not be fulfilled. So now you spread this value from X1 to X7. Suppose that you now choose another random variable, for example X5.



Now suppose you have a constraint that says: either X7 is false, or X6 is true, or X5 is false. So, I have X5 = true and X7 = true. This means that X6 should now also be true. Because otherwise this restriction would be violated. So, the system concludes that X6 should be true, and continues the process, performing the available checks and looking at all the available offers. The system checks if there are other things that are implied by the checks it has. And it follows these values ​​until one of two things happens.

The first is that you continue to follow the consequences and try random things, and eventually you set the value for each variable without ever encountering a contradiction. So you did everything right.

Second, you are faced with a contradiction, and then you return to the condition that caused X4 to be true, excluding the condition that caused X4 to be false. But there is one rule of Boolean algebra, which everyone should know: a variable cannot be both true and false.



And it says that you are faced with a contradiction, you obviously did something wrong in one of these random tasks that you tried to do.

Let's analyze this contradiction and see what kind of tasks led to this contradiction. Based on the tasks that led to this contradiction, let's think up a new conflict situation that summarizes this contradiction.

What happens that X1 is false, and X5 is false, and X9 is also false? Essentially, this is based on what I learned from these random quests, during which I discovered that one of these things must be true, that it cannot be so that X1 is true and X5 is true, and X9 is false, this can not be.

I know that this cannot happen, because when I tried to do this, everything “exploded”, I ended the program on a contradiction.

And so the SAT – solver tries to perform random tasks, checking how they pass. When it encounters contradictions, it analyzes the set of consequences that led to these contradictions, and ultimately forms a new constraint that ensures that the solver will never again encounter this particular contradiction, this particular problem.
Thus, we can imagine the SAT-solver as a “black box”, which gives a boolean constraint and can tell whether it is satisfactory or not. SMT solvers are based on the best SAT solvers. They can use the power of SAT solvers to solve NP-complete problems with subject-oriented reasoning about supported theories.

To get an idea of ​​how this works, let's assume that you have such a formula.



Is it doable? Can we find a satisfying check for her? The SMT solver can separate a part of this formula that requires reasoning in the theory of integers. We use Boolean structures to separate formulas. So we have the formulas F1, F2, F3 and F4.



Now this is a purely logical, boolean task - can I find a satisfactory task for this? The SAT solver can say: “yes, I can find something that satisfies this task by making F1 = true, F2 = true and F3 = true”. This satisfies the assignment of a Boolean formula.

\

So, now we have a question that we can ask the solver for a specific area, in this case it’s just a linear arithmetic solver. So we can go to the Theory solver linear solver and say, "The SAT solver claims that this is a reasonable assignment, and that if I can get this assignment to work, then my formula will be satisfied."

I can say that F1 is X> 5, F2 is Y <5, and F3 is Y> X. So I can ask the SAT solver whether you can get X and Y such that X is> 5, Y is < 5, while Y would be> X? Now it is a question of purely linear arithmetic, there is no Boolean logic.

And what is the answer to this question? Not. To satisfy these conditions at the same time is impossible.
So, there are traditional methods for solving linear problems. You can use the simplex method, for example, to solve systems of linear inequalities. There are many methods that can be used to solve systems of linear inequalities.



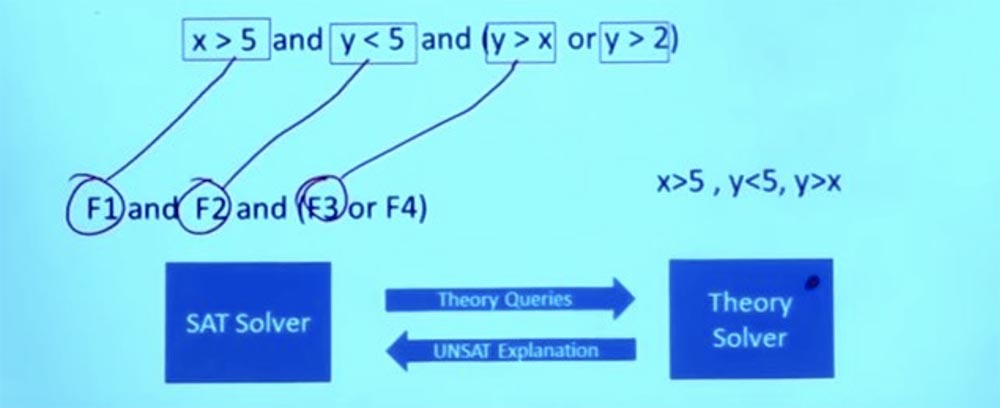
So, the SAT solver sends theoretical questions to the theoretical solver Theory solver. The bottom line is that the Theory solver solvers know all about these problems and can give an exact answer to the question whether these conditions will work.

In this case, the theoretical solver processes the request, finds out that the given assignment of conditions cannot work, returns to the SAT solver and says: “the things that you did will not work”!

But he doesn’t just say “yes” or “no”, but explains why something will not work. From the fact that these formulas do not work, Theory solver concludes that F1 and F2 and F3 cannot exist simultaneously, and tells the SAT solver that these 3 formulas are mutually exclusive.

So now we have some information that I can return to the SAT solver and ask him: “Hey, you can give me a solution that satisfies not only the constraint that we had at the beginning, but also the new constraint that Theory found solver?

Is there any other purpose that now satisfies both of these limitations?



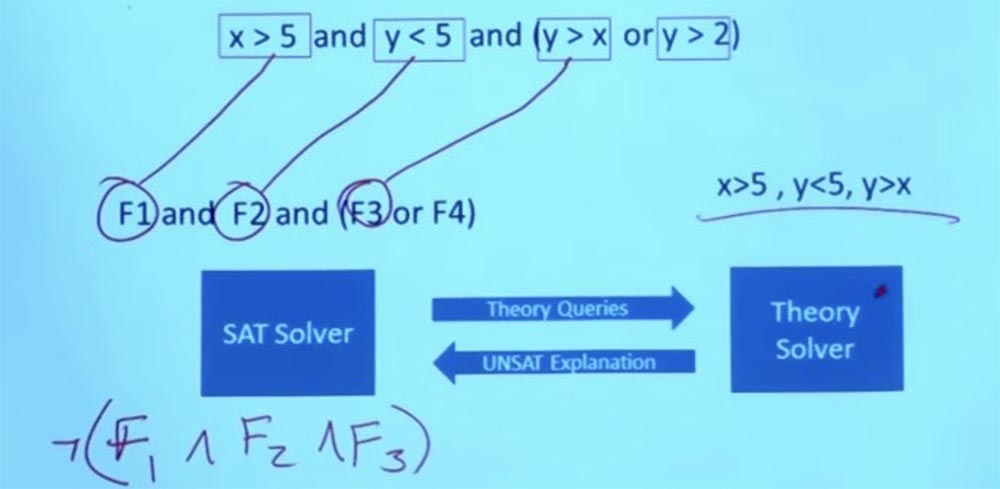
So, we discard the original constraint X> 5, Y <5, Y> X, we do not care anymore.



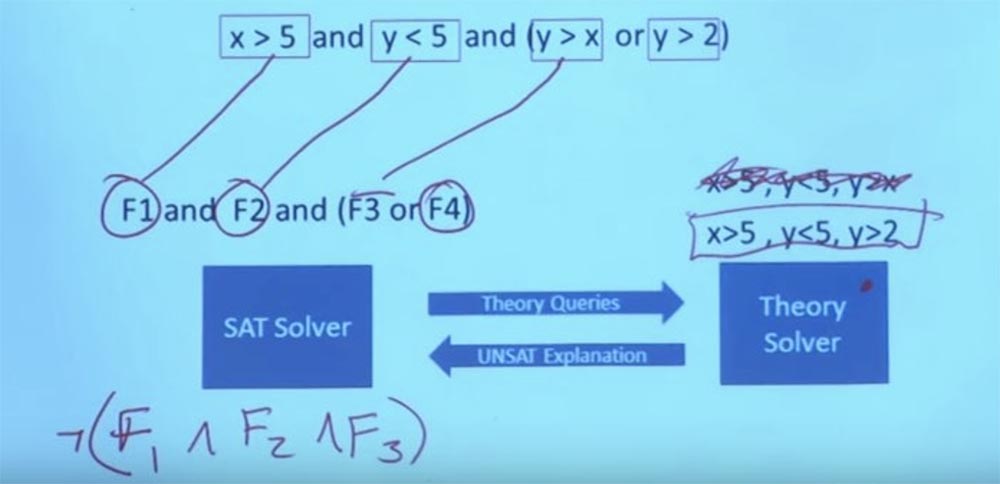
We have a new constraint that we can set our Theory solver - X> 5, Y <5, Y> 2. We can make Y equal 3, and X equal 6, and then it will work. Now you have a task that satisfies the formula in the theory and satisfies the boolean structure for this purpose. And with this, the system can come back and say: "Yes, here is a task that satisfies all your limitations." This is the interaction between the Theory solver and the SAT solver. In fact, this means being able to talk about very, very large and very complex Boolean formulas. This is what makes symbolic execution possible.

Now we will consider the next question - how is the transition from the program to the limitations that we can provide to the SMT solver.

Audience: Is building an SMT solver an NP-complete task or not?

Professor: SMT – solver is in fact itself a canonical NP-complete problem. But the majority of solvers today also include the support of some theories that are completely insoluble.

Audience: how to approach this issue in your system?

Professor: well, in the end, you get a restriction created from this program. You are going to give it to the SMT solver. And the fact that these are NP-complete tasks or the fact that they are not satisfactory means that if you are lucky, you will get an answer in a matter of seconds. But if you are unlucky, it may take longer than the creation of the universe took.



Audience: Does it happen that the tasks of the linear system do not pass the SAT?

Professor: yes, that really happens. However, the available engineering tools make it happen less and less. We do not solve random problems of SAT, we do not solve completely random problems of bit vectors.

We solve problems that have a certain structure, so that a person can look at it and have some confidence that it will work. We are trying to create in his head some arguments for understanding why this worked. And SAT solvers use this structure. Your problem may have a million boolean variables, but in fact most of these variables are very dependent on each other’s values. Thus, the number of degrees of freedom in a problem is actually much smaller than millions of variables suggest.

Audience: you say that this is not an exam question, but real life. Once someone has built this system, it should work and make sense. So this probably will not be one of the useless theoretical talk.

Professor: that's it. Therefore, in practice, when you use this tool, what you always do is set timeouts. In general, everything happens because exponentiality does not mean that you cannot do this. Exponentiality, that is, when one function is limited to another function, simply means that there is a brick wall in front of which these things will work, and they will work really very quickly. Exponentiality works in both directions.



When you move away from this wall, things grow very quickly, but when you get closer to smaller or simpler problems, these problems also accelerate very, very quickly. This means that many problems end very quickly. And then there is a timeout of problems. The point is to design things in such a way that among those problems that quickly end there are problems that are of practical use. These are problems that point you to the security vulnerabilities of your system, to errors on the path that you may not have investigated before, or on input data that would break your path if you did not examine them in advance.

So, we know how to move from a formula, from a set of constraints to an answer, which either says: “Yes, this formula has a solution, and here it is, this solution”. Or he will say: “this formula is unsatisfactory, because there is no input data satisfying your assignments”. So how do we get the formula from the program?

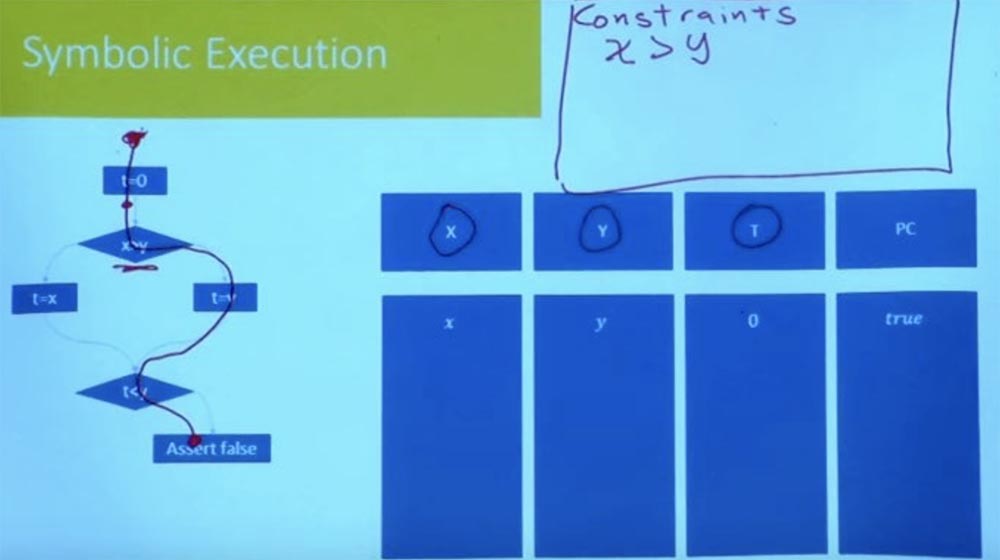
When you do symbolic execution, go to the branch and don’t know in which direction it will go. There are two possibilities for what to do in this case. — , , , .

, , . , SMT-. . , .

: « , , , , ».

, , . . , .

, . , , . , – , . ? , .



, , t=0 false.



, , ? : , , .

, , , , , , .

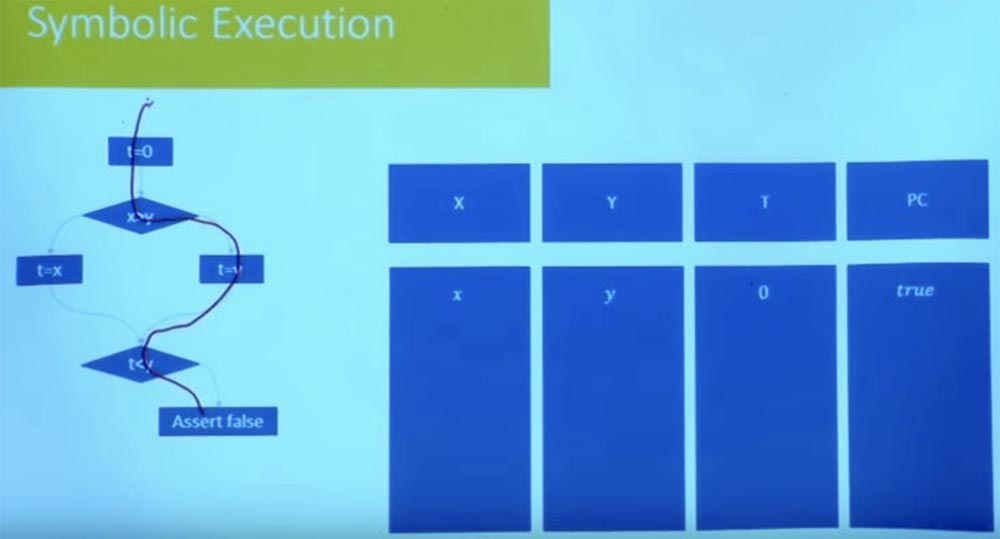
, , t = 0, x, y 0. , . , , X , Y.

, X > Y.



55:00

MIT « ». 10: « », 3


.

Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending to friends, 30% discount for Habr users on a unique analogue of the entry-level servers that we invented for you: The whole truth about VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps from $ 20 or how to share the server? (Options are available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps until December for free if you pay for a period of six months, you can order here .

Dell R730xd 2 times cheaper? 2 Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 $249 ! Read about How to build an infrastructure building. class c using servers Dell R730xd E5-2650 v4 worth 9000 euros for a penny?