We calculate the "magic squares" using the GPU
Hello habr.
The theme of "magic squares" is quite interesting, because on the one hand, they have been known since antiquity, on the other hand, the calculation of the "magic square" even today represents a very difficult computational problem. Recall that to build the “magic square” of NxN, you need to enter the numbers 1..N * N so that the sum of its horizontals, verticals and diagonals is equal to the same number. If you just go through the number of all the options for arranging numbers for a 4x4 square, then we get 16! = 20,922,789,888,000 options.
Consider how this can be done more effectively.
')

To begin with, we repeat the problem statement It is necessary to arrange the numbers in the square so that they do not repeat, and the sum of the horizontals, verticals and diagonals was equal to the same number.
It is easy to prove that this sum is always the same, and is calculated by the formula for any n:
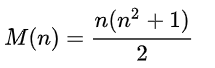
We will consider 4x4 squares, so the sum = 34.
Let's designate all variables through X, our square will look like this:
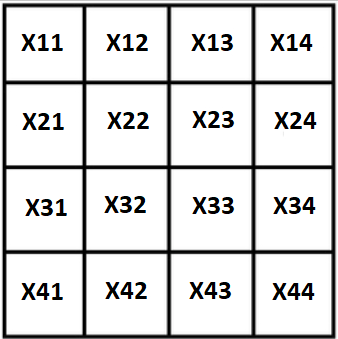
The first, and obvious, property: the sum of the square is known, the extreme Stoblots can be expressed in terms of the remaining 3:
Thus, a 4x4 square actually turns into a 3x3 square, which reduces the number of enumeration options from 16! up to 9! 57m times Knowing this, let's start writing the code, let's see how complicated such a search is for modern computers.
The principle of the program is very simple. We take the set of numbers 1..16 and the for loop on this set, it will be x11. Then we take the second set consisting of the first except for the number x11, and so on.
A rough view of the program looks like this:
The full text of the program can be found under the spoiler.
Result: 7040 variants of “magic squares” 4x4 were found, and the search time was 102s .

By the way, it is interesting to check whether there is the same one in the list of squares that is depicted in Durer's engraving. Of course there is, because The program displays all 4x4 squares:
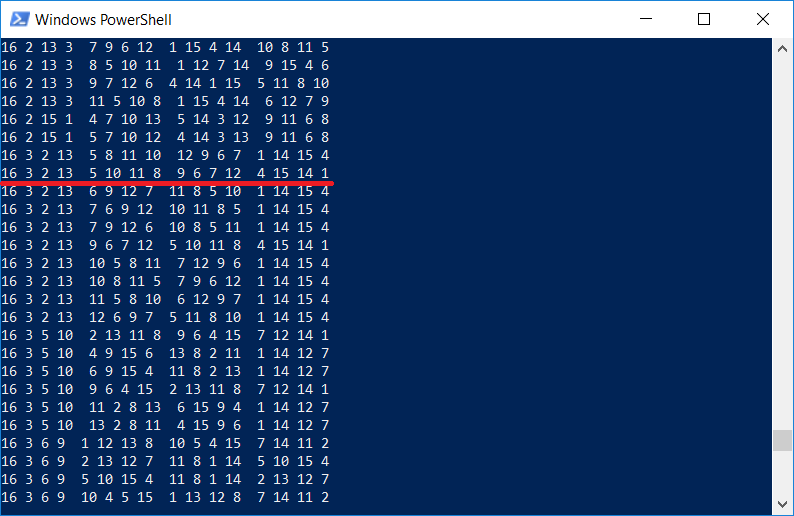
It should be noted that Durer put a square in the image for a reason, the figures 1514 also indicate the year of the engraving.
As you can see, the program works (note the task as verified at 1514 by Albrecht Dürer;), however, the execution time is not so short for a computer with a Core i7 processor. Obviously, the program runs in one thread, and it is advisable to use all the other cores.
Rewriting a program using streams is basically easy, although a bit cumbersome. Fortunately, there is an option almost forgotten today - using OpenMP (Open Multi-Processing) support. This technology has existed since 1998, and allows processor directives to tell the compiler which parts of the program to execute in parallel. OpenMP support is also available in Visual Studio, so to make a program multi-threaded, just add one line to the code:
The #pragma omp parallel for for directive indicates that the next for loop can be executed in parallel, and the additional parameter squares specifies the name of a variable that will be common for parallel threads (without this, the increment does not work correctly).
The result is obvious: the execution time has been reduced from 102s to 18s .

This is much better - because the task is almost perfectly parallelized (the calculations in each branch are independent of each other), the time is less than about a number of times equal to the number of processor cores. But alas, it is important not to get more out of this code, although some optimizations can and can win a few percent. Moving on to heavier artillery, GPU calculations.
If you do not go into details, then the computation process that runs on a video card can be represented as several parallel hardware blocks (blocks), each of which executes several processes (threads).
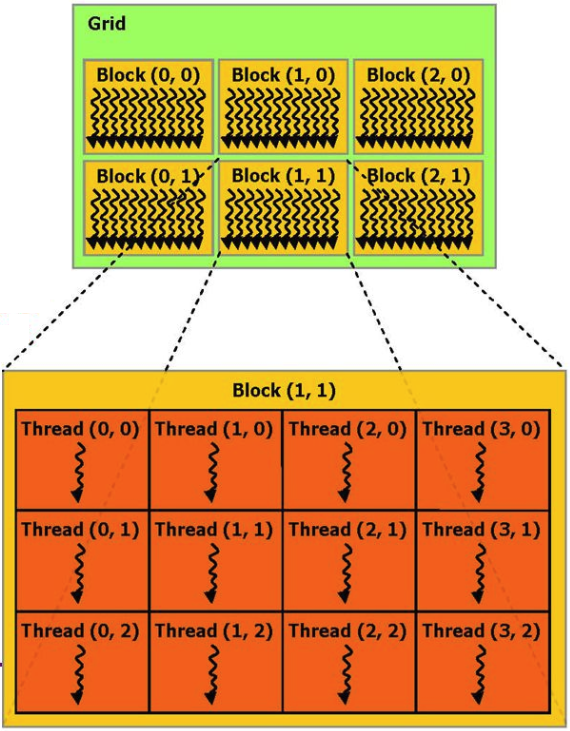
For example, you can give an example of the addition function of 2 vectors from the CUDA documentation:
The x and y arrays are common to all blocks, and the function itself is thus executed simultaneously on several processors. The key here is in parallelism - the video card processors are much simpler than a regular CPU, but there are a lot of them and they are focused specifically on processing numerical data.
That's what we need. We have a matrix of numbers X11, X12, .., X44. Run the process of 16 blocks, each of which will perform 16 processes. The block number will match the X11 number, the process number the X12 number, and the code itself will calculate all possible squares from for the selected X11 and X12. Everything is simple, but there is one subtlety here - you need to not only calculate the data, but also transfer it back from the video card; for this, we will store the number of squares found in the zero element of the array.
The main code is quite simple:
We allocate a memory block on a video card using cudaMalloc, run the squares function, specifying 2 parameters 16.16 (the number of blocks and the number of streams) corresponding to the enumerated numbers 1..16, then copy the data back through cudaMemcpy.
The squares function itself essentially repeats the code from the previous part, with the difference that the increment in the number of found squares is done with the help of atomicAdd - this guarantees that the variable will correctly change during simultaneous calls.
The result does not require comments - the runtime was 2.7s , which is about 30 times better than the original single-threaded version:

As suggested in the comments, you can use even more hardware blocks of the video card, so that a variant of 256 blocks was tried. Minimal code change:
This reduced the time by 2 times, to 1.2s . Further, on each block, you can run 16 processes, which gives the best time of 0.44s .
Most likely, this is far from ideal, for example, you can run even more blocks on the GPU, but this will make the code more complicated and difficult to understand. And of course, the calculations are not "free" - with the loaded GPU, the Windows interface starts to slow down noticeably, and the computer's power consumption increases almost 2 times, from 65 to 130W.
Edit : as the Bodigrim user suggested in the comments, one more equality holds for the 4x4 square: the sum of 4 “internal” cells is equal to the sum of “external”, it is also equal to S.

This will speed up the algorithm by expressing some variables through others and removing another 1-2 nested loops, an updated version of the code can be found in the comment below.
The task of finding "magic squares" turned out to be technically very interesting, and at the same time difficult. Even with calculations on the GPU, the search for all 5x5 squares can take several hours, and the optimization to search for magic squares of dimension 7x7 and higher remains to be done.
Mathematically and algorithmically, there are also some unresolved points:
On the analysis and properties of the magic squares themselves, you can write a separate article, if there is interest.
PS: To the question that will surely follow, "why is it necessary." In terms of energy consumption, the calculation of magic squares is no better or worse than the calculation of bitcoins, so why not? In addition, this is an interesting warm-up for the mind and an interesting task in the field of application programming.
The theme of "magic squares" is quite interesting, because on the one hand, they have been known since antiquity, on the other hand, the calculation of the "magic square" even today represents a very difficult computational problem. Recall that to build the “magic square” of NxN, you need to enter the numbers 1..N * N so that the sum of its horizontals, verticals and diagonals is equal to the same number. If you just go through the number of all the options for arranging numbers for a 4x4 square, then we get 16! = 20,922,789,888,000 options.
Consider how this can be done more effectively.
')

To begin with, we repeat the problem statement It is necessary to arrange the numbers in the square so that they do not repeat, and the sum of the horizontals, verticals and diagonals was equal to the same number.
It is easy to prove that this sum is always the same, and is calculated by the formula for any n:
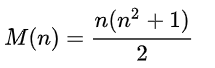
We will consider 4x4 squares, so the sum = 34.
Let's designate all variables through X, our square will look like this:

The first, and obvious, property: the sum of the square is known, the extreme Stoblots can be expressed in terms of the remaining 3:
X14 = S - X11 - X12 - X13
X24 = S - X21 - X22 - X23
...
X41 = S - X11 - X21 - X31Thus, a 4x4 square actually turns into a 3x3 square, which reduces the number of enumeration options from 16! up to 9! 57m times Knowing this, let's start writing the code, let's see how complicated such a search is for modern computers.
C ++ - single-flow version
The principle of the program is very simple. We take the set of numbers 1..16 and the for loop on this set, it will be x11. Then we take the second set consisting of the first except for the number x11, and so on.
A rough view of the program looks like this:
int squares = 0; int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); for (int x11 = 1; x11 <= MAX; x11++) { Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; ... int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; // , printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); squares++; } } printf("CNT: %d\n", squares); The full text of the program can be found under the spoiler.
Entire source code
#include <set> #include <stdio.h> #include <ctime> #include "stdafx.h" typedef std::set<int> Set; typedef Set::iterator SetIterator; #define N 4 #define MAX (N*N) #define S 34 int main(int argc, char *argv[]) { // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 const clock_t begin_time = clock(); int squares = 0; int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); for (int x11 = 1; x11 <= MAX; x11++) { Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; Set set21(set13); set21.erase(x13); set21.erase(x14); for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) { int x21 = *it21; Set set22(set21); set22.erase(x21); for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) { int x22 = *it22; Set set23(set22); set23.erase(x22); for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) { int x23 = *it23, x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; Set set31(set23); set31.erase(x23); set31.erase(x24); for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) { int x31 = *it31; Set set32(set31); set32.erase(x31); for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) { int x32 = *it32; Set set33(set32); set33.erase(x32); for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) { int x33 = *it33, x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); squares++; } } } } } } } } } printf("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); return 0; } Result: 7040 variants of “magic squares” 4x4 were found, and the search time was 102s .

By the way, it is interesting to check whether there is the same one in the list of squares that is depicted in Durer's engraving. Of course there is, because The program displays all 4x4 squares:

It should be noted that Durer put a square in the image for a reason, the figures 1514 also indicate the year of the engraving.
As you can see, the program works (note the task as verified at 1514 by Albrecht Dürer;), however, the execution time is not so short for a computer with a Core i7 processor. Obviously, the program runs in one thread, and it is advisable to use all the other cores.
C ++ - multithreaded version
Rewriting a program using streams is basically easy, although a bit cumbersome. Fortunately, there is an option almost forgotten today - using OpenMP (Open Multi-Processing) support. This technology has existed since 1998, and allows processor directives to tell the compiler which parts of the program to execute in parallel. OpenMP support is also available in Visual Studio, so to make a program multi-threaded, just add one line to the code:
int squares = 0; #pragma omp parallel for reduction(+: squares) for (int x11 = 1; x11 <= MAX; x11++) { ... } printf("CNT: %d\n", squares); The #pragma omp parallel for for directive indicates that the next for loop can be executed in parallel, and the additional parameter squares specifies the name of a variable that will be common for parallel threads (without this, the increment does not work correctly).
The result is obvious: the execution time has been reduced from 102s to 18s .

Entire source code
#include <set> #include <stdio.h> #include <ctime> #include "stdafx.h" typedef std::set<int> Set; typedef Set::iterator SetIterator; #define N 4 #define MAX (N*N) #define S 34 int main(int argc, char *argv[]) { // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 const clock_t begin_time = clock(); int squares = 0; #pragma omp parallel for reduction(+: squares) for (int x11 = 1; x11 <= MAX; x11++) { int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; Set set21(set13); set21.erase(x13); set21.erase(x14); for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) { int x21 = *it21; Set set22(set21); set22.erase(x21); for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) { int x22 = *it22; Set set23(set22); set23.erase(x22); for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) { int x23 = *it23, x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; Set set31(set23); set31.erase(x23); set31.erase(x24); for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) { int x31 = *it31; Set set32(set31); set32.erase(x31); for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) { int x32 = *it32; Set set33(set32); set33.erase(x32); for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) { int x33 = *it33, x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); squares++; } } } } } } } } } printf("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); return 0; } This is much better - because the task is almost perfectly parallelized (the calculations in each branch are independent of each other), the time is less than about a number of times equal to the number of processor cores. But alas, it is important not to get more out of this code, although some optimizations can and can win a few percent. Moving on to heavier artillery, GPU calculations.
Calculations with NVIDIA CUDA
If you do not go into details, then the computation process that runs on a video card can be represented as several parallel hardware blocks (blocks), each of which executes several processes (threads).

For example, you can give an example of the addition function of 2 vectors from the CUDA documentation:
__global__ void add(int n, float *x, float *y) { int index = threadIdx.x; int stride = blockDim.x; for (int i = index; i < n; i += stride) y[i] = x[i] + y[i]; } The x and y arrays are common to all blocks, and the function itself is thus executed simultaneously on several processors. The key here is in parallelism - the video card processors are much simpler than a regular CPU, but there are a lot of them and they are focused specifically on processing numerical data.
That's what we need. We have a matrix of numbers X11, X12, .., X44. Run the process of 16 blocks, each of which will perform 16 processes. The block number will match the X11 number, the process number the X12 number, and the code itself will calculate all possible squares from for the selected X11 and X12. Everything is simple, but there is one subtlety here - you need to not only calculate the data, but also transfer it back from the video card; for this, we will store the number of squares found in the zero element of the array.
The main code is quite simple:
#define N 4 #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) int main(int argc,char *argv[]) { const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<<MAX, MAX>>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p<SQ_MAX && p<squares; p++) { int i = MAX*p + 1; printf("[%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d]\n", results[i], results[i+1], results[i+2], results[i+3], results[i+4], results[i+5], results[i+6], results[i+7], results[i+8], results[i+9], results[i+10], results[i+11], results[i+12], results[i+13], results[i+14], results[i+15]); } printf ("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); cudaFree(gpu_out); free(results); return 0; } We allocate a memory block on a video card using cudaMalloc, run the squares function, specifying 2 parameters 16.16 (the number of blocks and the number of streams) corresponding to the enumerated numbers 1..16, then copy the data back through cudaMemcpy.
The squares function itself essentially repeats the code from the previous part, with the difference that the increment in the number of found squares is done with the help of atomicAdd - this guarantees that the variable will correctly change during simultaneous calls.
Whole source code
// Compile: // nvcc -o magic4_gpu.exe magic4_gpu.cu #include <stdio.h> #include <ctime> #define N 4 #define MAX (N*N) #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) #define S 34 // Magic square: // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 __global__ void squares(int *res_array) { int index1 = blockIdx.x, index2 = threadIdx.x; if (index1 + 1 > MAX || index2 + 1 > MAX) return; const int x11 = index1+1, x12 = index2+1; for(int x13=1; x13<=MAX; x13++) { if (x13 == x11 || x13 == x12) continue; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; for(int x21=1; x21<=MAX; x21++) { if (x21 == x11 || x21 == x12 || x21 == x13 || x21 == x14) continue; for(int x22=1; x22<=MAX; x22++) { if (x22 == x11 || x22 == x12 || x22 == x13 || x22 == x14 || x22 == x21) continue; for(int x23=1; x23<=MAX; x23++) { int x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x23 == x11 || x23 == x12 || x23 == x13 || x23 == x14 || x23 == x21 || x23 == x22) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; for(int x31=1; x31<=MAX; x31++) { if (x31 == x11 || x31 == x12 || x31 == x13 || x31 == x14 || x31 == x21 || x31 == x22 || x31 == x23 || x31 == x24) continue; for(int x32=1; x32<=MAX; x32++) { if (x32 == x11 || x32 == x12 || x32 == x13 || x32 == x14 || x32 == x21 || x32 == x22 || x32 == x23 || x32 == x24 || x32 == x31) continue; for(int x33=1; x33<=MAX; x33++) { int x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x33 == x11 || x33 == x12 || x33 == x13 || x33 == x14 || x33 == x21 || x33 == x22 || x33 == x23 || x33 == x24 || x33 == x31 || x33 == x32) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; const int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x44 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; // Square found: save in array (MAX numbers for each square) int p = atomicAdd(res_array, 1); if (p >= SQ_MAX) continue; int i = MAX*p + 1; res_array[i] = x11; res_array[i+1] = x12; res_array[i+2] = x13; res_array[i+3] = x14; res_array[i+4] = x21; res_array[i+5] = x22; res_array[i+6] = x23; res_array[i+7] = x24; res_array[i+8] = x31; res_array[i+9] = x32; res_array[i+10] = x33; res_array[i+11] = x34; res_array[i+12]= x41; res_array[i+13]= x42; res_array[i+14] = x43; res_array[i+15] = x44; // Warning: printf from kernel makes calculation 2-3x slower // printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); } } } } } } } } int main(int argc,char *argv[]) { int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<<MAX, MAX>>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p<SQ_MAX && p<squares; p++) { int i = MAX*p + 1; printf("[%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d]\n", results[i], results[i+1], results[i+2], results[i+3], results[i+4], results[i+5], results[i+6], results[i+7], results[i+8], results[i+9], results[i+10], results[i+11], results[i+12], results[i+13], results[i+14], results[i+15]); } printf ("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); cudaFree(gpu_out); free(results); return 0; } The result does not require comments - the runtime was 2.7s , which is about 30 times better than the original single-threaded version:

As suggested in the comments, you can use even more hardware blocks of the video card, so that a variant of 256 blocks was tried. Minimal code change:
__global__ void squares(int *res_array) { int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX; ... } squares<<<MAX*MAX, 1>>>(gpu_out); This reduced the time by 2 times, to 1.2s . Further, on each block, you can run 16 processes, which gives the best time of 0.44s .
Final Code
#include <stdio.h> #include <ctime> #define N 4 #define MAX (N*N) #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) #define S 34 // Magic square: // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 __global__ void squares(int *res_array) { int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX, index3 = threadIdx.x; if (index1 + 1 > MAX || index2 + 1 > MAX || index3 + 1 > MAX) return; const int x11 = index1+1, x12 = index2+1, x13 = index3+1; if (x13 == x11 || x13 == x12) return; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) return; if (x14 == x11 || x14 == x12 || x14 == x13) return; for(int x21=1; x21<=MAX; x21++) { if (x21 == x11 || x21 == x12 || x21 == x13 || x21 == x14) continue; for(int x22=1; x22<=MAX; x22++) { if (x22 == x11 || x22 == x12 || x22 == x13 || x22 == x14 || x22 == x21) continue; for(int x23=1; x23<=MAX; x23++) { int x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x23 == x11 || x23 == x12 || x23 == x13 || x23 == x14 || x23 == x21 || x23 == x22) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; for(int x31=1; x31<=MAX; x31++) { if (x31 == x11 || x31 == x12 || x31 == x13 || x31 == x14 || x31 == x21 || x31 == x22 || x31 == x23 || x31 == x24) continue; for(int x32=1; x32<=MAX; x32++) { if (x32 == x11 || x32 == x12 || x32 == x13 || x32 == x14 || x32 == x21 || x32 == x22 || x32 == x23 || x32 == x24 || x32 == x31) continue; for(int x33=1; x33<=MAX; x33++) { int x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x33 == x11 || x33 == x12 || x33 == x13 || x33 == x14 || x33 == x21 || x33 == x22 || x33 == x23 || x33 == x24 || x33 == x31 || x33 == x32) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; const int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x44 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; // Square found: save in array (MAX numbers for each square) int p = atomicAdd(res_array, 1); if (p >= SQ_MAX) continue; int i = MAX*p + 1; res_array[i] = x11; res_array[i+1] = x12; res_array[i+2] = x13; res_array[i+3] = x14; res_array[i+4] = x21; res_array[i+5] = x22; res_array[i+6] = x23; res_array[i+7] = x24; res_array[i+8] = x31; res_array[i+9] = x32; res_array[i+10] = x33; res_array[i+11] = x34; res_array[i+12]= x41; res_array[i+13]= x42; res_array[i+14] = x43; res_array[i+15] = x44; // Warning: printf from kernel makes calculation 2-3x slower // printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); } } } } } } } int main(int argc,char *argv[]) { int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<<MAX*MAX, MAX>>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p<SQ_MAX && p<squares; p++) { int i = MAX*p + 1; printf("[%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d]\n", results[i], results[i+1], results[i+2], results[i+3], results[i+4], results[i+5], results[i+6], results[i+7], results[i+8], results[i+9], results[i+10], results[i+11], results[i+12], results[i+13], results[i+14], results[i+15]); } printf ("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); cudaFree(gpu_out); free(results); return 0; } Most likely, this is far from ideal, for example, you can run even more blocks on the GPU, but this will make the code more complicated and difficult to understand. And of course, the calculations are not "free" - with the loaded GPU, the Windows interface starts to slow down noticeably, and the computer's power consumption increases almost 2 times, from 65 to 130W.
Edit : as the Bodigrim user suggested in the comments, one more equality holds for the 4x4 square: the sum of 4 “internal” cells is equal to the sum of “external”, it is also equal to S.

X22 + X23 + X32 + X33 = X11 + X41 + X14 + X44 = SThis will speed up the algorithm by expressing some variables through others and removing another 1-2 nested loops, an updated version of the code can be found in the comment below.
Conclusion
The task of finding "magic squares" turned out to be technically very interesting, and at the same time difficult. Even with calculations on the GPU, the search for all 5x5 squares can take several hours, and the optimization to search for magic squares of dimension 7x7 and higher remains to be done.
Mathematically and algorithmically, there are also some unresolved points:
- The dependence of the number of "magic squares" on N. It is known that a 2x2 square does not exist, 3x3 squares exist only 8 (but essentially 1, its other reflections or turns), 4x4 squares, as we found out, 7040, but the exception is turns or reflections in the algorithm not added. For large dimensions, the question is still open.
- The exclusion of squares, which are turns or reflections already found.
- Speed and optimization algorithm. Unfortunately, testing the code on a supercomputer or at least on NVIDIA Tesla is not possible, if someone can run, it would be interesting. If anyone has ideas on the algorithm itself, you can also try to implement them. If you wish, you can even run a distributed project to search for squares, if of course enough of the number of readers is typed;)
On the analysis and properties of the magic squares themselves, you can write a separate article, if there is interest.
PS: To the question that will surely follow, "why is it necessary." In terms of energy consumption, the calculation of magic squares is no better or worse than the calculation of bitcoins, so why not? In addition, this is an interesting warm-up for the mind and an interesting task in the field of application programming.
Source: https://habr.com/ru/post/424845/
All Articles