How big can a solar-powered drone be?

The idea seems ingenious: to place solar batteries on the drone, and then he will not need a battery. Without it, the drone can be controlled while the sun is shining. This is wonderful (assuming your intentions are pure). This is exactly what the students at Singapore National University have done.

But from the video it is clear that their drone is as flat as a sheet. Therefore, in reality, the question is: what mass and size can such a device have so that it can rise into the air solely on solar energy? I will answer this question and give you a special calculator for quadcopters on solar batteries.

Solar power

Power is energy per unit of time, measured in watts. Ideally, you need to redirect all the energy from the solar panels in flight. This means that no battery is needed for temporary storage of energy - and this is good, because it would only increase the mass. But how much energy can you squeeze out of the solar panel? This is the real problem.

The energy output of solar cells depends on the following values:
')

• The power of the sun. The power of solar energy on the surface of the Earth is about 1000 watts per square meter. This value cannot be changed without changing the Sun (which is not recommended) (E)
• The size of the solar battery. The larger the battery, the more power. Let's start with 0.04 m ² (A)
• Efficiency of the solar battery. Just because 1000 W / m ² falls on the panel does not mean that all this energy will turn into electricity. It seems to me a reliable figure of 28% (e)
• Orientation angle It is better if sunlight falls perpendicular to the panel. But the Sun, most likely, will not be right at the zenith. What about angle θ = 45 °?

As a result, we obtain the energy output according to the following equation:

$$

$$P = e A E cos \ theta$$

And this is solar power.

Flight energy

Calculate the energy of flight quadcopter a little more difficult. However, this calculation will be true for any aircraft flying upward with the help of a support on the air.

Let's start with the nature of forces and movement. To give speed to a subject at rest, force is required. The size of the force depends on the mass of the object, the magnitude of the speed and the time it takes to change. Replace the item on the air - it is used by our flight machines. Reactive force can be increased by using a large mass of air or a large area of ​​the rotor. It can also be increased by increasing the air velocity.

Quadcopter thrust simulation

The aerodynamics of a rotating main rotor cannot be called trivial. However, such problems did not stop me earlier on the way to building a simplified model. In the next, extremely simplified physical model, I will assume that the thrust of the helicopter appears due to a change in the momentum of the downward moving air. To achieve sufficient thrust for helicopter flight, we have two options. You can take a small screw and push the air very quickly down, or take a large screw and push the air more slowly.

If the screw area is A and the air density is ρ, then the lift force is expressed in terms of air velocity by the following equation:

$$

$$F_ {lift} = {{dp_ {air}} \ over {dt}} = {{\ rho A v ^ 2} \ over {2}}$$

What about power? Power is the change in the kinetic energy of air divided by the time interval. The faster the air, the greater the kinetic energy and the shorter the time span. I cited the complete derivation of this formula in an article about a flying machine on muscular strength . Here is the expression for power.

$$

$$P = {{\ rho A v ^ 3} \ over {4}}$$

Since power is proportional to the cube of air velocity, for a helicopter on muscular strength, it must be small, and, therefore, the helicopter must be large. So it is .

Now to my favorite graphics. I knew that my model could be completely untenable, so I studied the data on real helicopters. Based on the mass and size of the propeller, you can calculate the power of the flight and compare it with the specified engine power. Here is a graph — calculated power versus specified power for some helicopters.



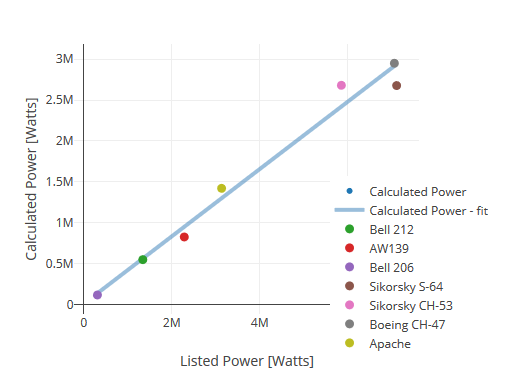
I was very surprised by the linearity of the data.

More helicopter data

A friend of mine who was fond of creating his own quadcopter showed me the T-Motor website , which lists a lot of electric motors and data on their efficiency. Here are the characteristics indicated there:

• The size.
• Voltage.
• Current.
• Thrust depending on the throttle.
• Rotational speed.
• Power - the product of current and voltage.

What can you do about it? Since I have the size and thrust of the screw, I can calculate the air velocity. It can be used to calculate the theoretical power and compare with that. That's what I got.



Yeah. Still linear relationship. Here I was a little worried - it seemed unlikely that my simplified model of the helicopter thrust would work on such a scale. Moreover, even the slope of the graphs looks like - 0.656 and 0.411. What does this slope mean? It means that my estimated power is about 2 times less. If you record power, like:

$$

$$P = {{\ rho A v ^ 3} \ over {2}}$$

Then the calculated power will coincide with the specified. Not sure where the deuce came from. Perhaps I made a mistake by taking the derivative when calculating the average air velocity.

If we have the data, we can build another chart, a bonus one. The dependence of my calculated air velocity on the speed of rotation of the screw.



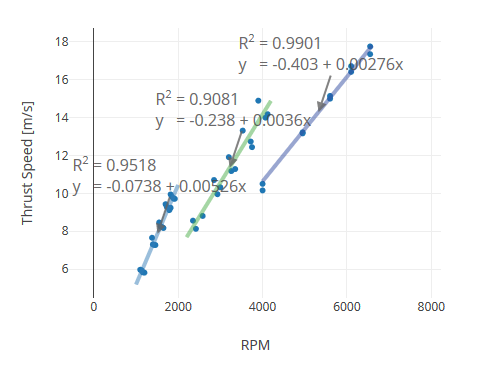
What does it mean? The faster the propeller blades rotate, the faster the air moves. I suspect that another variable matters here - the slope of the blades.

Back to solar

But we do not need traction, we need power. Increasing air velocity increases its kinetic energy. The faster the kinetic energy increases, the more power is required for this.



This means that you can make an aircraft with small screws that push the air very quickly, or with a large screw that pushes the air slower. But the energy of these two options is different. The kinetic energy is proportional to the square of the speed, so the smaller propeller needs much more energy to fly. Therefore, a real helicopter on muscular strength must be so huge that it has enough human energy.

Calculation of flight power

Instead of taking into account all possible options for the size of the quadrocopter, screws and solar panels, as well as their efficiency, I simply made a calculator - a Python program that counts the size of the screw necessary for the device to fly at the given parameters.

With my initial estimations, I got a screw diameter of 5.9 cm. Sounds believable. And all the options with an increase in mass or a change in the size of solar panels can now be calculated on a calculator.