The theory of happiness. Thermodynamics of class inequality
I continue to acquaint Habr's readers with chapters from my book “The Theory of Happiness” with the subtitle “Mathematical foundations of the laws of meanness”. This is not a published popular science book, very informally telling how mathematics allows you to look at the world and life of people with a new degree of awareness. It is for those who are interested in science and for those who are interested in life. And since our life is complex and, by and large, unpredictable, the emphasis in the book is mainly on probability theory and mathematical statistics. Here theorems are not proved and the fundamentals of science are not given; this is by no means a textbook, but what is called recreational science. But it is this almost playful approach that allows us to develop intuition, brighten up lectures for students with vivid examples, and, finally, explain to nemathematicians and our children what we found so interesting in our dry science.
In this chapter, we will discuss money, markets, and entropy, as well as look at animated gifs, which, alas, cannot be printed in a booklet.
')

Of the whole mass of problems solved by mathematical economics, we consider only one - how does it turn out that even under equal conditions for all market participants and a fair exchange of funds the poor become more than rich and why even an ideal mathematical society is prone to financial inequality. Well, in passing, we learn something curious about mathematical statistics and the distribution of random variables.
I am a physicist by education and by profession, and my professional deformation is expressed in a peculiar view of the world, as on a wide variety of physical systems and processes. From the point of view of physics, the real market is a substantially non-stationary open system, with many degrees of freedom, in which stochastic (random) processes play an important role. In this sense, the market is similar to the subject of studying such areas of physics as thermodynamics and statistical physics, in which, due to the inability to consider all the innumerable details and the behavior of all components of the system, go to its generalizing and measurable properties, such as energy, temperature or pressure . It is not surprising that attempts at a thermodynamic description of economic systems and the creation of econophysics have been made for more than a hundred years. But the trouble is: while scientists are examining the details, summarizing the knowledge gained and leading disputes about fundamental laws, the main object of study is economic reality, it has time to change beyond recognition. Her behavior seems to be trying to preserve, or even increase, her uncertainty and unpredictability.
A good example is the two-century history of using technical analysis when playing on the stock exchange. When a new powerful tool appears that allows you to grope hidden patterns and predict the course of a security or stock, it begins to bring profit to those who use it. But soon the market begins to “feel” new players and adapt to their strategy, the accuracy of predictions of the remarkable method begins to fall and, after some time, it falls into a large list of outdated and not very reliable tools. Neither modern flexible self-learning neural network algorithms, nor ultrafast robots-traders who perform millions of operations per minute, have not changed over the past two decades the main feature of the exchange game - its unpredictability. And until now, the main advantages of a professional in this industry are will, endurance of character, reluctance to excitement ... well, or possession of the exchange. Just like in a casino, where games are based on pure chance! On the one hand, this, of course, is insulting, but on the other - it gives reason to constantly improve methods and approaches. At one time, both the theory of probability and mathematical statistics were born from attempts to analyze gambling and economic games and only then found application in almost all natural sciences.
In further discussion, we will talk about money, but this familiar everyday-used category is surprisingly complex and ambiguous. The meaning and value of money depends on many factors, and by calling a certain amount of money out of context, we don’t say anything about its real value. This distinguishes monetary values from the majority of physical quantities that describe our world and makes it difficult to carry out rigorous arguments in the economy. But the purpose of our conversation: the mathematical foundations of the laws of meanness, everyday, clear and simple. Therefore, in the future, we will talk about certain “rubles”, meaning a formal ticket or a coin, and implying that the more these “rubles” are in someone, the “richer” they are. Other reasoning about the purchasing power, intangible or illiquid values, about "happiness is not in money", finally, we leave beyond the scope of the conversation.
We begin with an analysis of the validity of some simple distribution strategies of a known amount of money to a finite group of people.
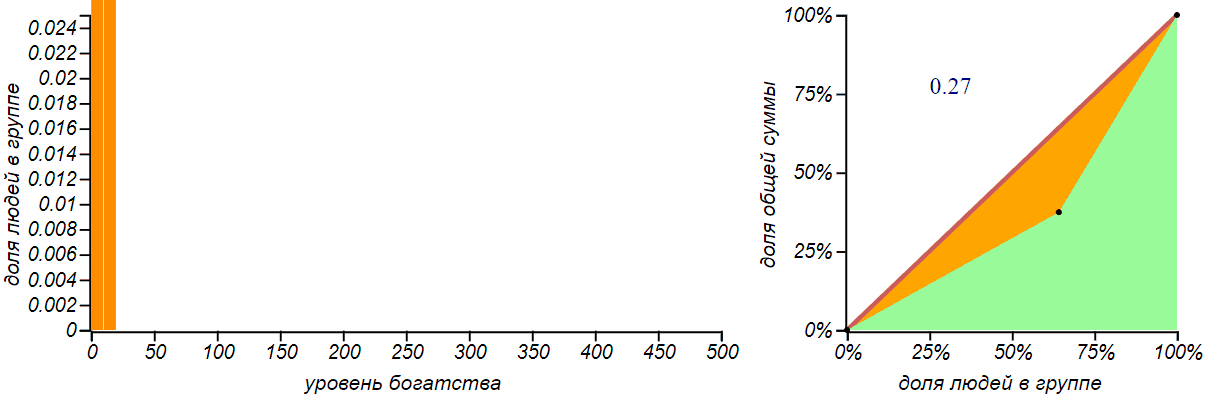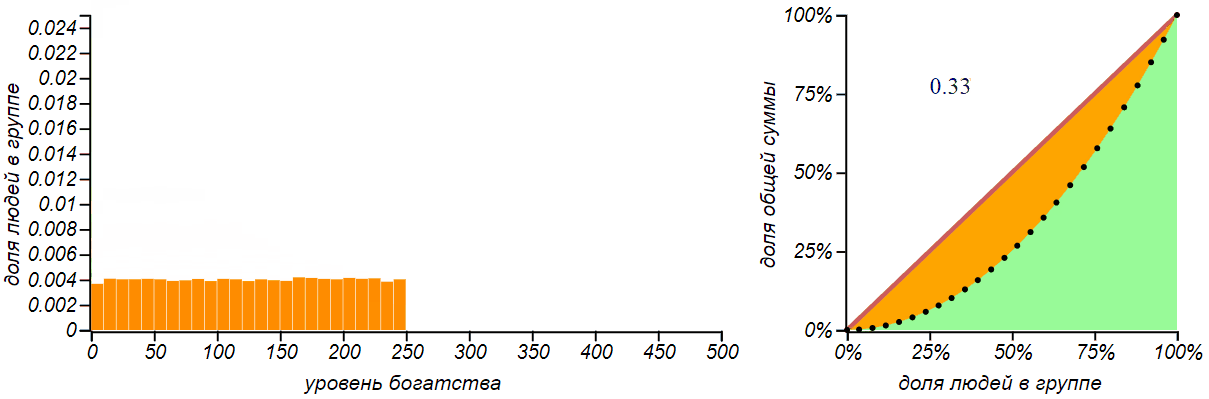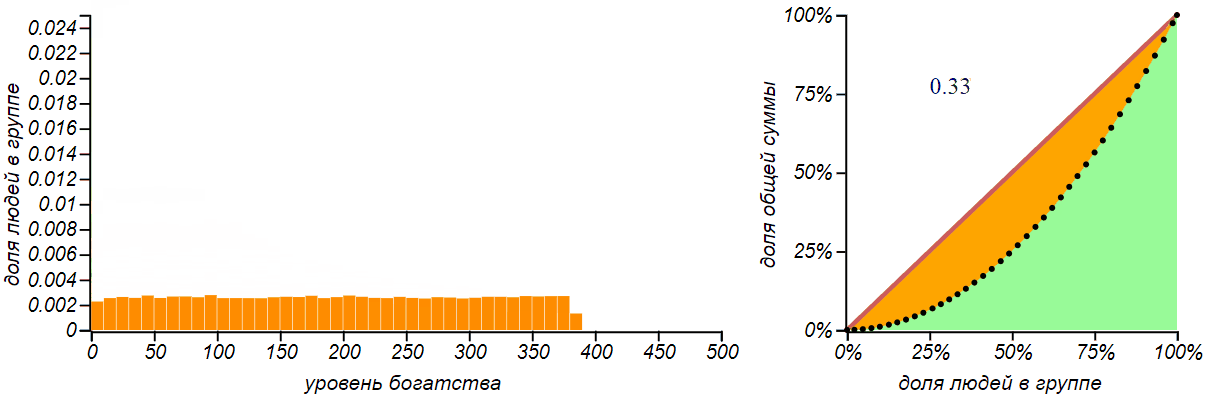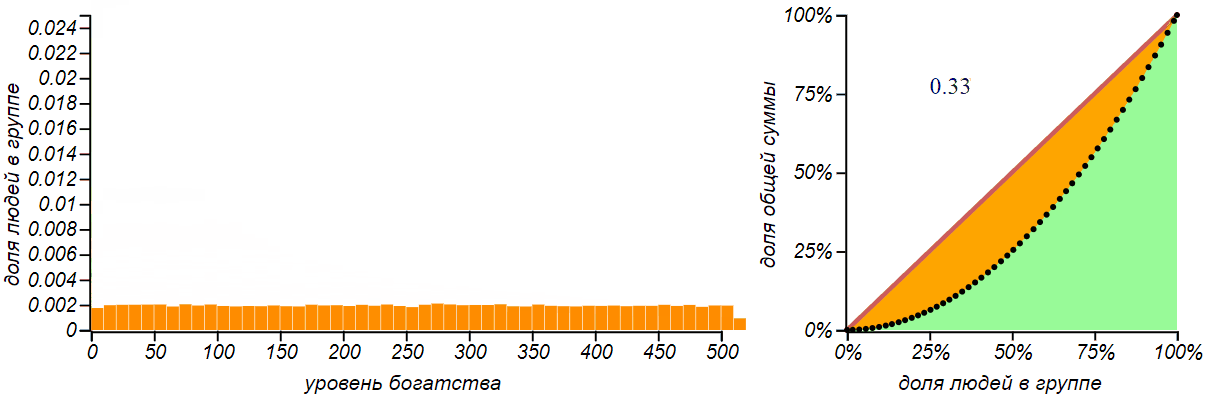
The first, most obvious strategy: “take everything, and divide”, that is, allocate each member of the group for an equal share of the total amount. Such a distribution is called degenerate , it has a Gini index equal to zero and corresponds to the equality curve on the Lorentz diagram.
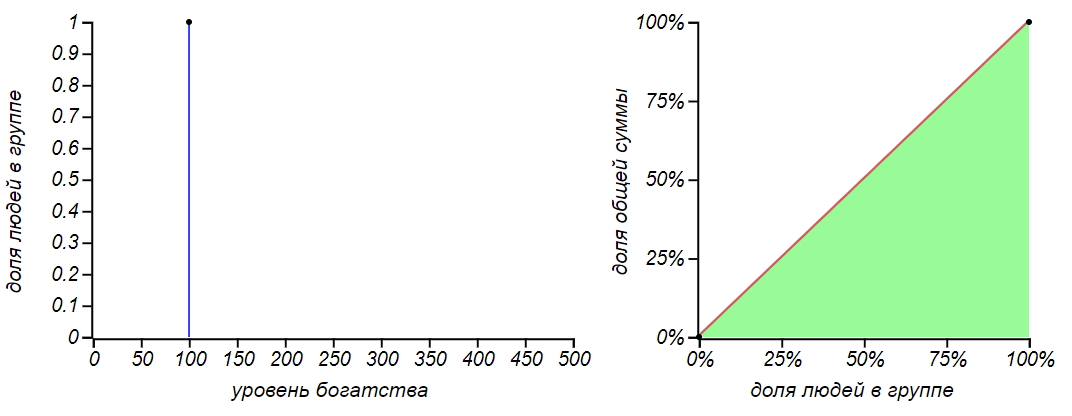
Absolutely fair degenerate distribution of money: everyone has everything equally.
Great option! Let's call it “Sharikov's strategy” in honor of the hero of the story of Mikhail Bulgakov “The Heart of a Dog”, who offered to solve all economic issues in this way.
The second, more realistic strategy is to distribute one ruble at random to each one. Who as lucky. We can call this strategy "Poisson" , since it is in this way that independent random events in the Poisson process are distributed on a time scale. For a group of n a person the probability of each of the participants to receive the ruble is 1 / n . After the distribution in this way M rubles, everyone should receive an amount equal to the number of such "positive" outcomes. The probability function for such a sum is well known - it is a binomial distribution , like a bell, symmetrically scattering around the mean M / n . Usually they are introduced to him by the example of calculating the probability of receiving a specified amount by throwing dice. For large values M the binomial distribution becomes almost indistinguishable from the normal one. Let's see how it will change, as money is distributed, the distribution of money in a group and its fairness.
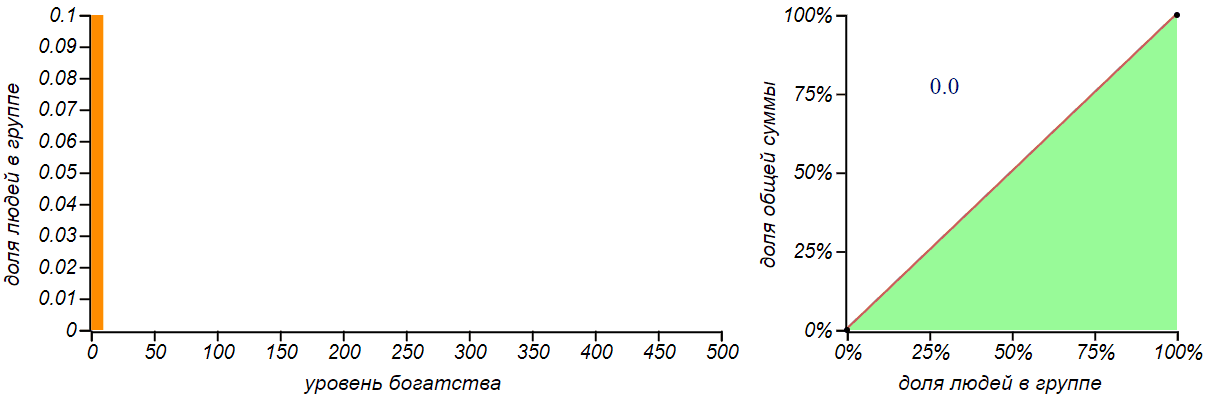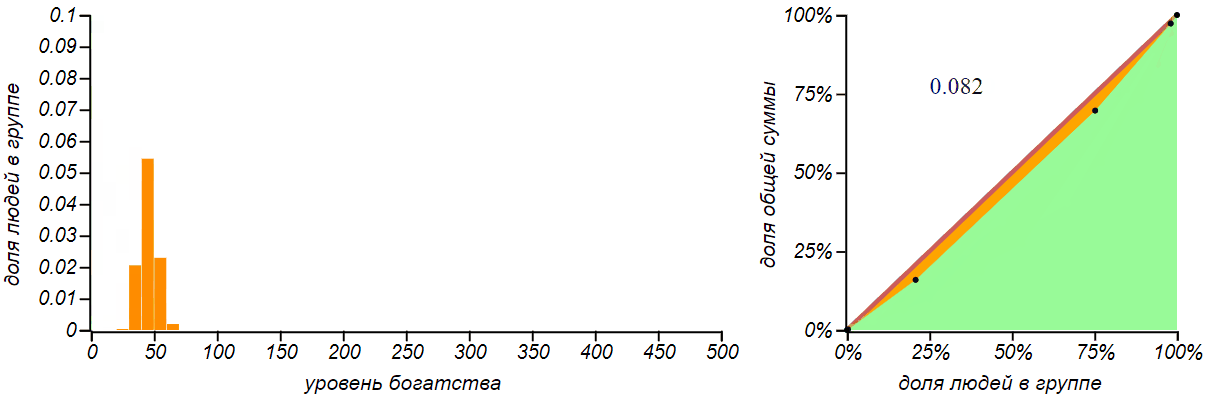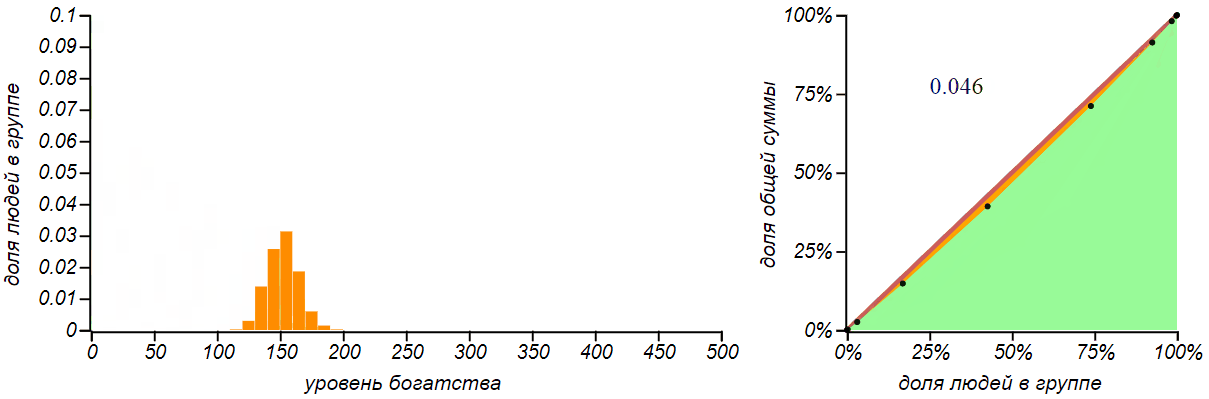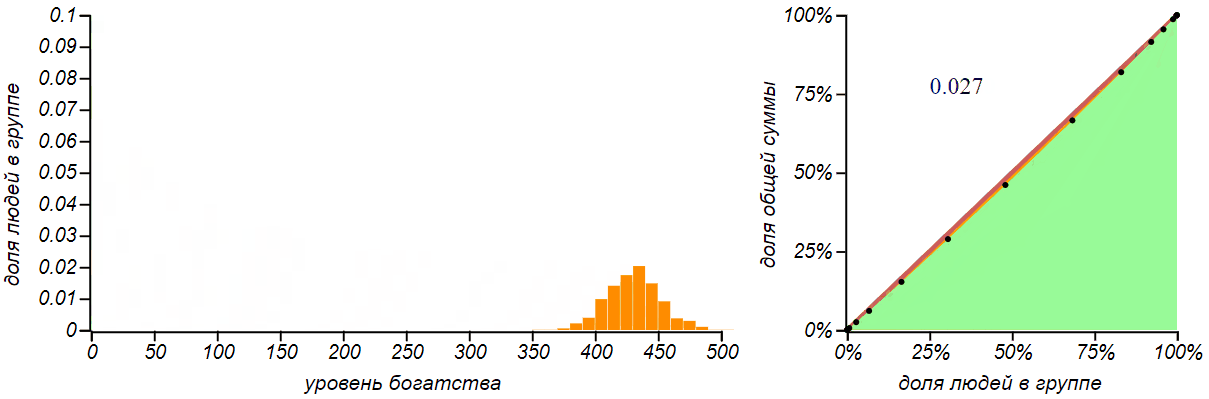
The result of the distribution of money according to the principle “to whom God will send” is the binomial distribution. The more money we distribute, the greater the value of the average and the spread, but the probability of not getting anything practically disappears.
This distribution, from the point of view of justice, looks very good, moreover, it becomes the fairer the more money we distribute to the public! Just great! It is a pity that society is not arranged and the rain of money does not pour on all of us equally.
For completeness, let's consider another simple artificial distribution of money - uniform . With this distribution, the poor will be as many as the rich.
Equal distribution does not mean that money is distributed evenly across all. With this distribution, the number of rich, poor and middle peasants is the same, but the money mainly belongs to the rich.
For a uniform distribution, the Lorenz curve is a quadratic parabola, and if the left boundary of the distribution is zero, then this parabola is independent of the position of the right boundary, and the Gini index for all such distributions is exactly 1 / 3 . Such an index value (but not such a distribution!) Was, for example, in the Australian economy in the 2000s - this is quite a good indicator.
However, the market is the market! The distributions discussed above are good, but require special conditions for their occurrence. If you give people the will to exchange money, change money for services, save them and squander in one night, the ideal distributions will lose stability and turn into some others.
Consider a group of n person. As a result of the revolution, we will distribute to all participants in the experiment at an equal amount of money - according to m rubles each, having received the most fair Sharikovskiy distribution of funds in society. Now we give them the freedom to get rich and get poorer by the will of their own destiny and build a primitive model of the market. We will ask someone randomly selected to give one ruble to any person in the group who was also chosen randomly. We say that this is the purchase of a certain service at a fixed price. The distribution of wealth is expected to change: someone will have less money, someone more. We will repeat the exchange procedure again and again and take a look at how the distribution of wealth in the group will change.
It is reasonable to think before the experiment, what we expect to see. The exchange of money between the participants is equally likely, as in the case of the Poisson strategy of distributing money, but at the same time the players lose money, moreover, by the same Poisson principle and with the same intensity. Thus, it can be assumed that both positive and negative increments will be normally distributed and arranged symmetrically with respect to zero. Each player, in the end, will receive the difference of these increments, which for two normally distributed random variables will also be normally distributed, in this case, around zero, since losses and gains are symmetrical.
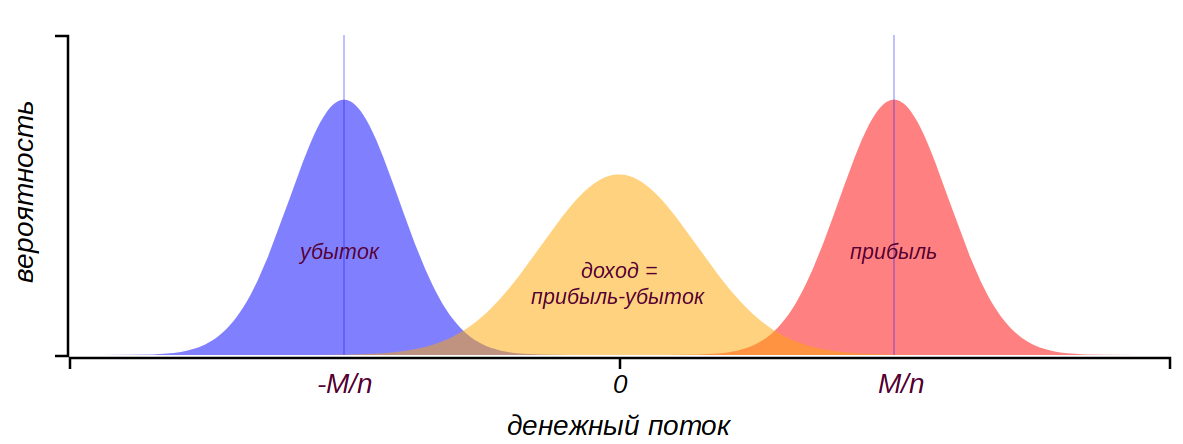
After a multitude of exchanges, each player will receive and lose an amount subordinate to a distribution close to normal. Total income will also be normally distributed around zero.
Thus, we get the classical random walk with normally distributed increments and we can expect some diffusion of means around the mean value m . The probability function should be blurred, increasing the variance with a constant average. It seems to be simple.
But there is a nuance. If, for some reason, someone from the group has no funds left, he will not be able to acquire services, giving money, but at the same time, can receive them. The possible value of welfare is limited to the left by zero, which means that the diffusion of wealth cannot spread infinitely and the observed probability function, sooner or later, will cease to be symmetrical.
There is another nuance. The amount of money in our closed system is limited and invariably, which means that random walks are not independent. Some lucky player will be able to get very large sums and get away from the ensemble very far, but only if the total mass is poorer. The participants in the experiment, using an invisible network, conserve the law of saving money in the system. What will the distribution of money in such conditions seek? It seems that the answer is not as obvious as it might seem at first glance, let's turn to simulation modeling and see what happens.
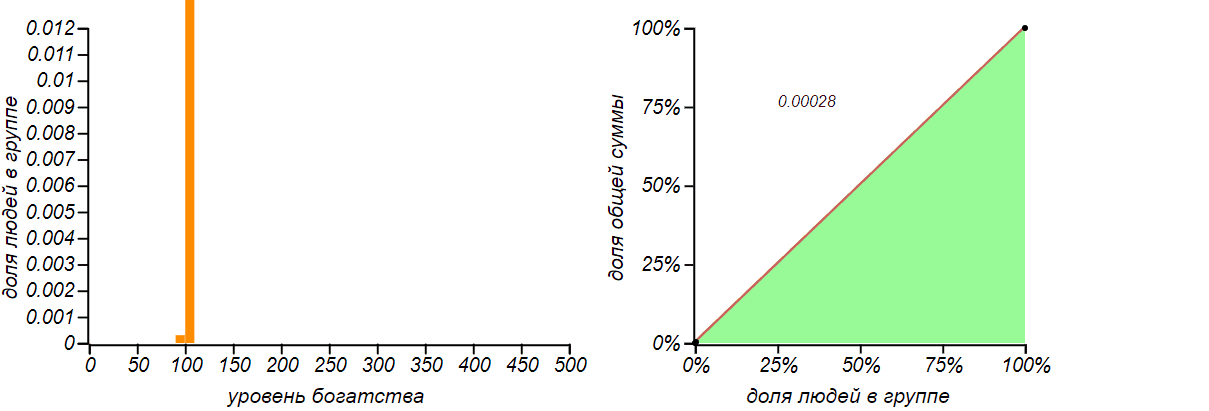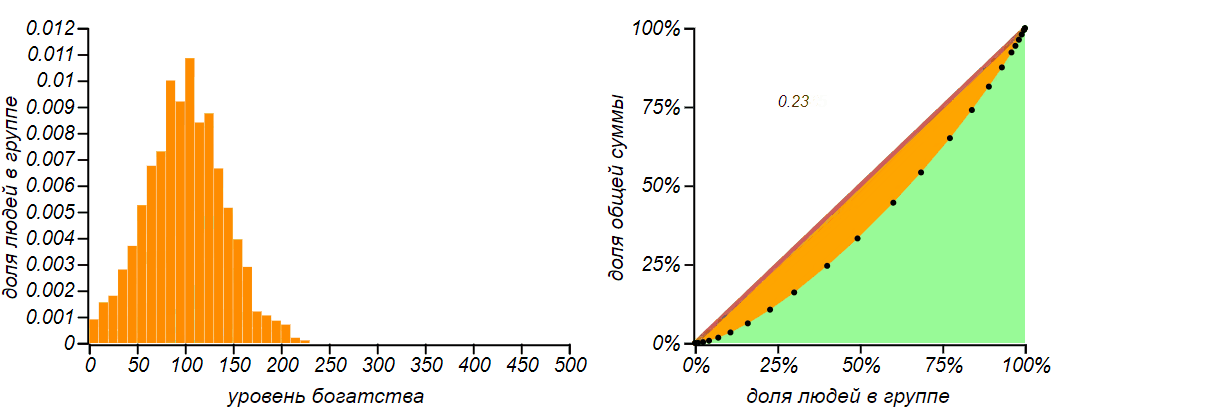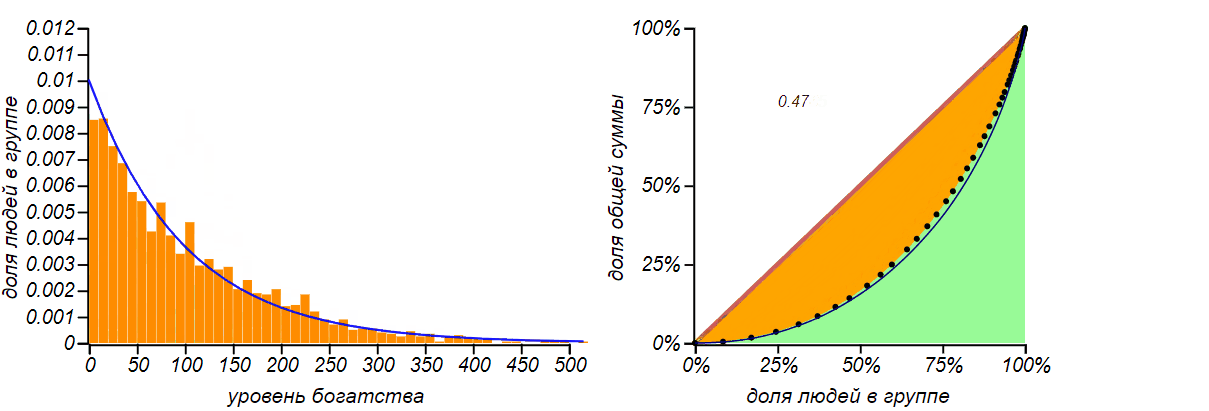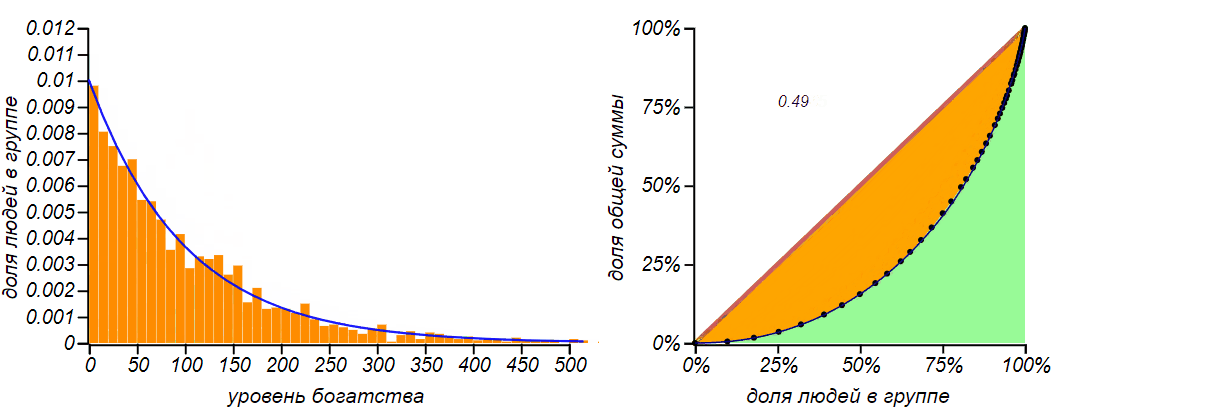
The result of simulation for the exchange of equal amount of money for n = 1000 and m = 100 . At first, a diffusion-like phenomenon is indeed observed, but as the probability function reaches the left boundary, the distribution tends to a characteristic asymmetric and not very fair form with a Gini coefficient close to 0.5 .
If this book is read by a physicist, then he will be able to confidently assume that this may be for distribution, he will call it a Gibbs distribution. An attentive reader may recall that we have already met with a similar picture and with such a Gini index, when we considered frustration while waiting for a bus. Then we considered the distribution of intervals between Poisson events, which was described by an exponential distribution. Both of these shrewd gentlemen will be right in calling the same remarkably distribution with different names.
Gibbs distribution is from the field of statistical physics. It describes the properties of systems, called the beautiful word "ensemble", which consist of a great number of interacting elements, most often particles. In an ensemble, you can select arbitrary subsystems (for example, individual particles or their groups) and assign certain state functions to them (these can be generalized coordinates, velocities, concentrations, chemical potentials, and much more). Using the methods of statistical physics, it is possible to explain and calculate the parameters of a wide variety of phenomena: chemical and catalytic processes, turbulence, ferromagnetism, the behavior of liquid crystals, superfluidity and superconductivity, and many others.
Gibbs distribution answers the question: what is the probability to meet a certain state of the subsystem, if given a) state energy, b) macroscopic (relatively speaking, global) properties of the system, such as temperature and c) it is known that the system is in thermodynamic equilibrium? It can be schematically expressed as follows:
The rigorous derivation of the expression for the Gibbs distribution is not needed here; instead, I want to show a beautiful purely mathematical argument leading to its exponential form. Since parts of a system are considered that give the whole system together, then as their characteristic it is worth choosing some additive value, that is, such that its value for the ensemble is the arithmetic sum of the values of its parts. Energy can be used as such in mechanics. On the other hand, we calculate the probability to observe a certain state of the system, and the probability is multiplicative , that is, if the system can be divided into parts, then the probability to observe all these parts will be equal to the product of the probabilities for the state of each of the parts. Thus, we need a function that turns an additive value into a multiplicative one. Only exponential function has this property. a x , the sum of the arguments turns into the product of the values: ax+y=axay. Well, of all the exponential functions, the exponential is the most convenient, since it behaves very well during integration and differentiation.
In our market model, we have an additive value - the amount of money each player has, it is an analogue of energy. With the exchange described by us, this quantity, like the energy in the physical system, is conserved. And what's the point here at the temperature? It's easy to figure out by looking at the expression for the probability density of the exponential distribution:
If to be completely accurate, and remember that money in our experiment is a discrete value, then we observe a geometric distribution - a discrete analog of the exponential. It is found in the task of counting the number of failures before the first win when throwing coins of varying degrees of honesty. These two distributions are similar and become indistinguishable with decreasing probability of winning. In our experiment, the chances of getting a ruble are equal 1/1000 , it is small enough to call the distribution exponential.
It remains to deal with the equilibrium of the final state of the market. Thermodynamic equilibrium can be described in different ways. First, the steady state must be in equilibrium , in which the system can be indefinitely long, without changing its macroscopic parameters, and not forming within itself ordered flows of matter and energy. Secondly, it must be sustainable , that is, if the system is out of balance, it will tend to return to it. Thirdly, this is the most probable state of the system, most often observed, which the system will eventually seek to get from any other, non-equilibrium one. Our experiment demonstrates these equilibrium criteria: having come to an exponential distribution, the system remains in it, moreover, it is easy to make sure in the experiment that from any arbitrary distribution we, after some time, will again come to the exponential. But this is not proof, but only a hint that we are most likely dealing with equilibrium. We need some kind of formal measurable criterion, which would unequivocally indicate to us that the system is in equilibrium without having to wait indefinitely or sort through all possible initial distributions. This would be a useful criterion that could be applied to the real market, without the need to conduct risky experiments on living people.
Reflections on equilibrium led physicists to the concept of entropy , which gradually went beyond thermodynamics and so liked scientists of all directions, philosophers and the general public that now entropy got an aura of mystery, incomprehensibility and God knows what else. A simple and special, in essence, the concept has gained in the minds of the broad masses a reputation as an inexplicable concept controlling the world. This is due to the fact that thermodynamics is a universal science that describes at a very high level the abstractions of a system of the most diverse nature: from physical, chemical and biological to social, economic and even purely humanitarian. After the school course, however, there is a feeling that thermodynamics is about a boring perfect gas, some kind of pistons and an impossible Carnot cycle. Such a very one-sided presentation is connected with the remarkable fact that thermodynamics, being one of the most abstract and universal branches of natural science, elegantly solves applied problems that are understandable to schoolchildren and are useful in industry. This cannot be said, for example, of category theory or topology — also very abstract, universal and, undoubtedly, useful disciplines, but in everyday tasks almost never encountered.
So entropy. The creator of thermodynamics, Clausius, and later Gibbs and Boltzmann, required a quantitative characteristic of equilibrium, which speaks of the probability of observing the indicated state of the system or its parts. Moreover, this quantity, reflecting the probability, multiplicative in nature, must be an additive state function, so that it can be calculated for the system, adding the values calculated for its parts. When we were looking for a suitable function for the Gibbs distribution, we proceeded from the fact that it should turn an additive argument into a multiplicative value. When searching for an expression for entropy, we need a function that is multiplicative in argument and additive in value — this is the logarithmic function, the inverse of the exponential. The entropy of the state of a complex system can be expressed as the expected value for the logarithm of the probability of observing the state of all its parts, or, according to Boltzmann, as the logarithm of the number of ways in which this state of the system can be realized. In this case, a more probable state corresponds to a higher value of entropy, and to an equilibrium state, the maximum possible one.
The number of ways to implement a particular state depends on the number of restrictions or conditions under which this state can be realized. The fewer such restrictions, the more probable the state is and the greater the value of its entropy. These restrictions and conditions make sense of the status information . Hence the idea that entropy reflects the degree of our ignorance about the system: the less we know about the state, the greater its entropy. Later, Shannon summarized this concept for any systems containing information, including the distributions of random variables. Here is what he did: for a random variable X determined by the probability function p(x) entropy is defined as follows:
This is how entropy changes as our market model comes to equilibrium.
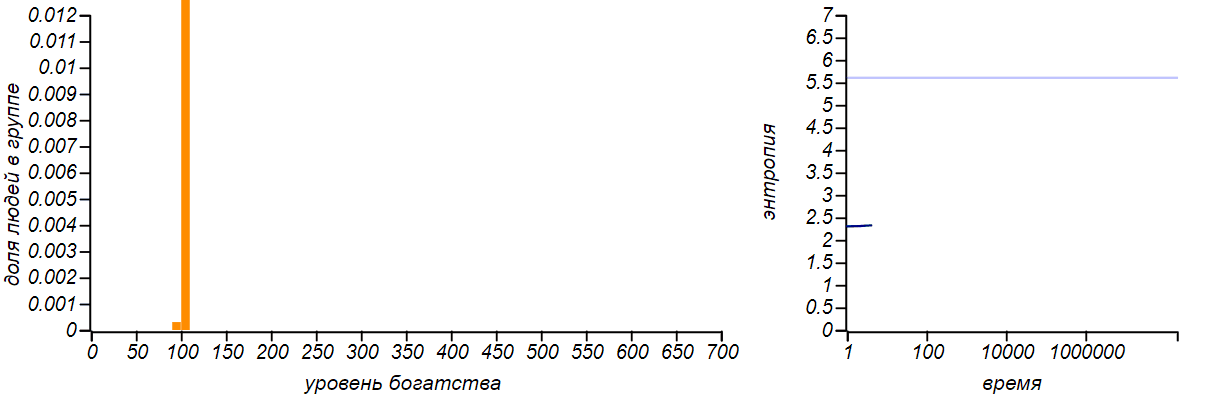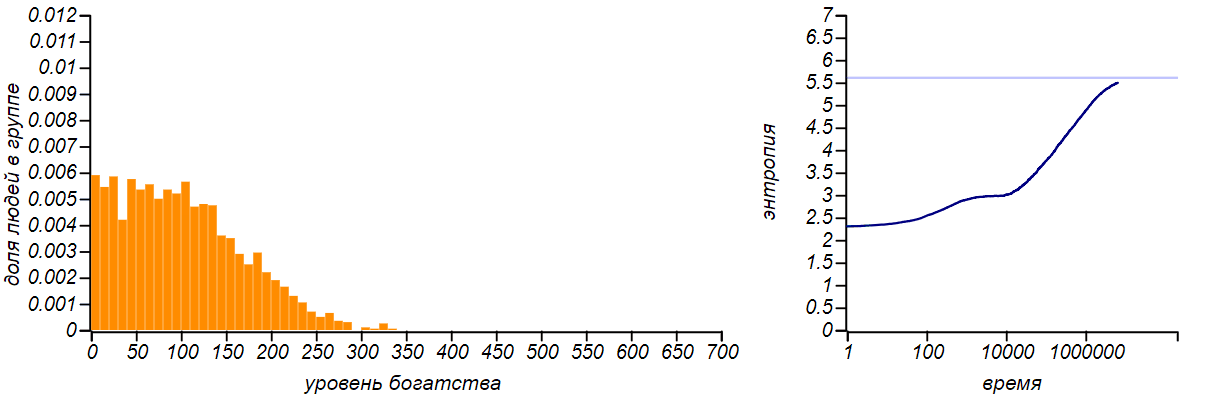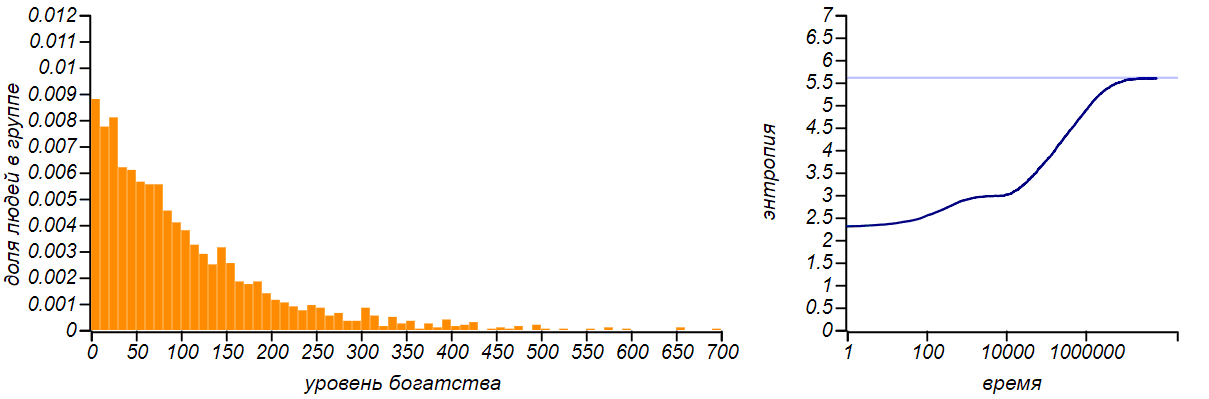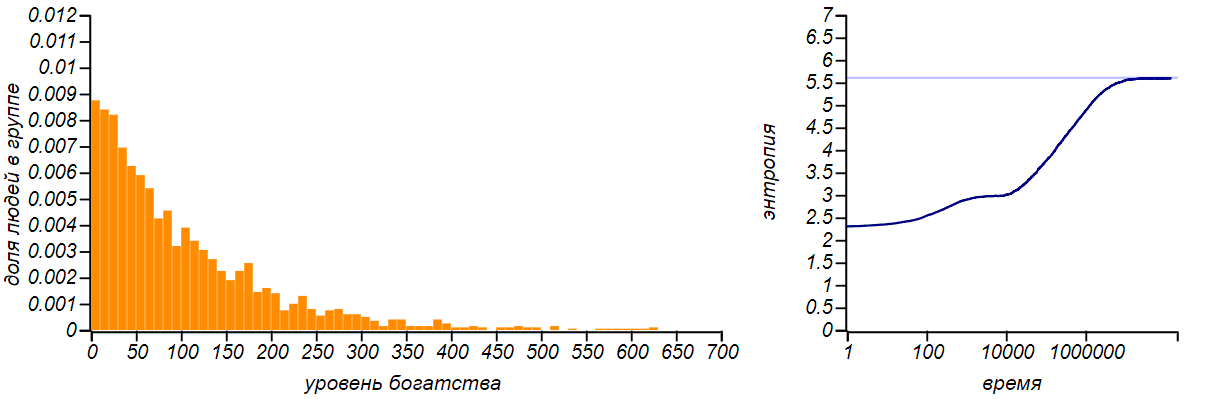
Entropy growth as the market approaches equilibrium. The horizontal line in the right graph shows the theoretical value of the entropy for the exponential distribution, equal to 1− ln( lambda) . The intermediate “shelf” corresponds to the period during which the distribution passed through the diffusion stage and was similar to the normal one.
Thus, to each distribution: given analytically or experimentally obtained in the form of a histogram, you can put in correspondence a positive number - its entropy. This means that the distributions can be compared with each other, determining more or less equilibrium and probable for given conditions. Moreover, for a certain class of distributions it is possible to distinguish a distribution with maximum entropy, and, moreover, only one. Classes are determined by constraints, or a measure of our knowledge of the statistical properties of a system. Here are some examples:
All familiar faces! These are very often used distributions that statistics apply to the widest class of problems. Their universality is due precisely to the fact that they, having the maximum entropy, are most likely and observable. Many distributions of real random variables aspire to them as equilibrium. The most free of restrictions among all others is the normal distribution: it requires a minimum of information about the random variable. Less is no longer possible: if we indicate only the mean value, then in an effort to increase entropy, the distribution will be “spread out” along the entire numerical axis.But, if we know only the mean value, but at the same time we restrict the random value to positive values, then the equilibrium distribution will be unambiguous - exponential. This is the case that we observed in our experiment with the market. We knew in advance only how much money we gave to each player and the fact that the amount of money in the system was constant, it fixed the average value. And since the money we have is a positive value, most likely in equilibrium we will get an exponential distribution of wealth with a Gini index equal1 / 2 .
There are many modifications of the model described by us: the exchange can take place not by one ruble, but by a random variable, limited by the state of the giver, while you can give money not to any one player, but distribute it randomly. Until we introduce new parameters into the game, all these modifications do not change the form of the equilibrium distribution of wealth - it remains exponential. You can make sure of this with the help of simulation modeling, but it’s not interesting to provide pictures for various exchange methods - they are all the same. Many researchers have noted this feature of market models. An interesting model is built by Dragulescu and Yakovenko from the University of Maryland, in which players are united into certain companies and further simulated is the interaction of companies with employee-players and buyers-players.But even in this complex case, the exponential distribution is indifferent, indifferent to the model parameters chosen.
To demonstrate the universality of the principle of maximum entropy, let us artificially limit the level of an individual player’s wealth from above, forbidding him to receive money if he already has some fixed amount. The equilibrium distribution, of course, will change. And if the right border is equal to twice the average value, then we come to the case described in the first row of the table. Indeed, by limiting a random variable to a finite segment and not indicating anything more, we cannot assume any other expected value of the average, except the middle of this segment. Therefore, the equilibrium distribution in this case should be uniform. Let's check, is it?
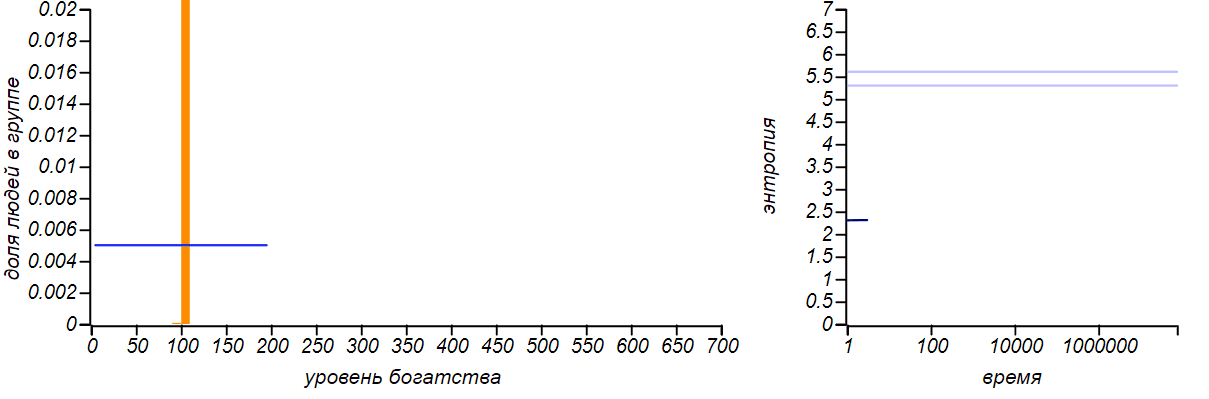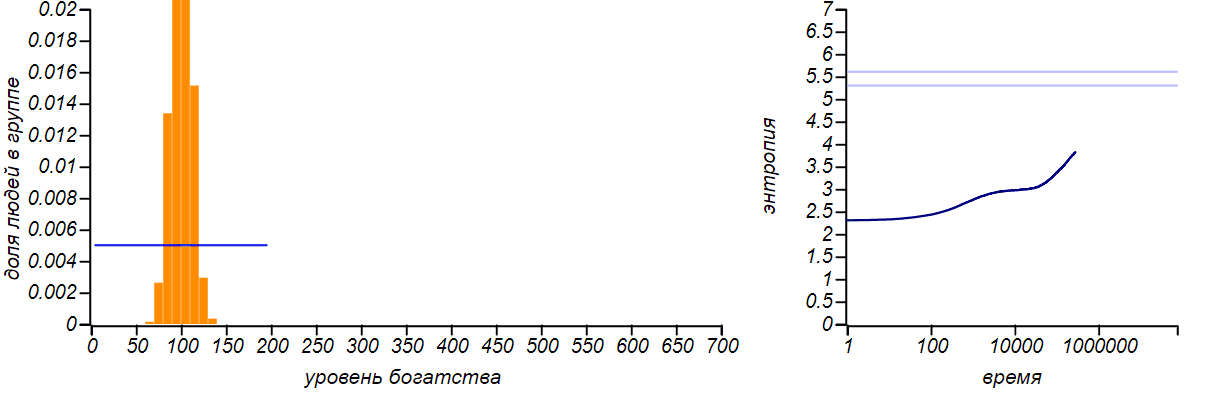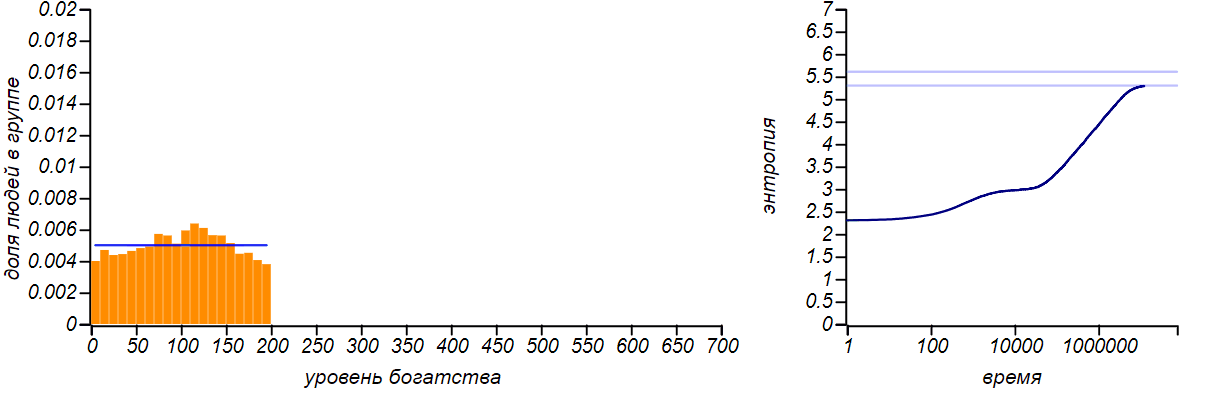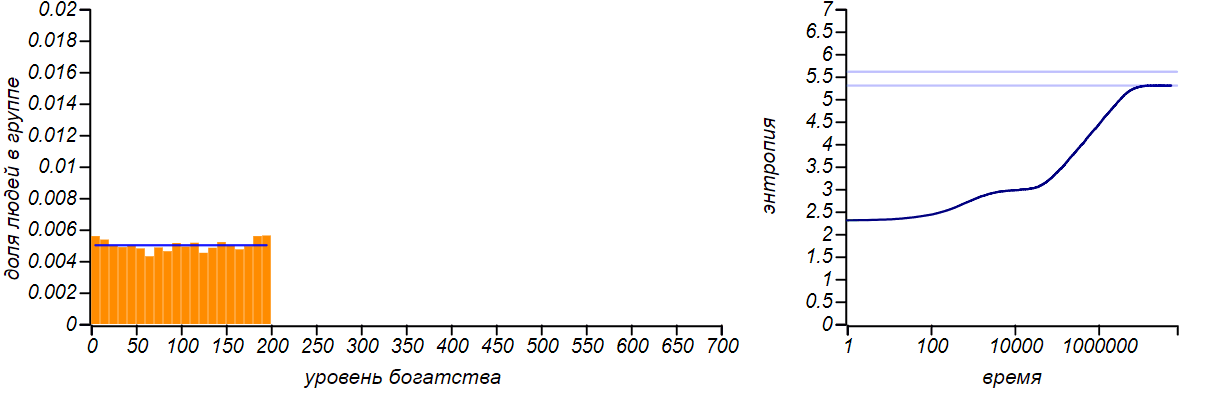
This is what happens when the upper limit of the possible level of player wealth is limited, and, in such a way, that the upper limit is exactly twice the average value. According to the principle of maximum entropy, the equilibrium distribution should be uniform. The horizontal line on the right graph shows the theoretical value of entropy for uniform distribution.
And what will happen in case of symmetry breaking, that is, if we move the right border to the right or left?
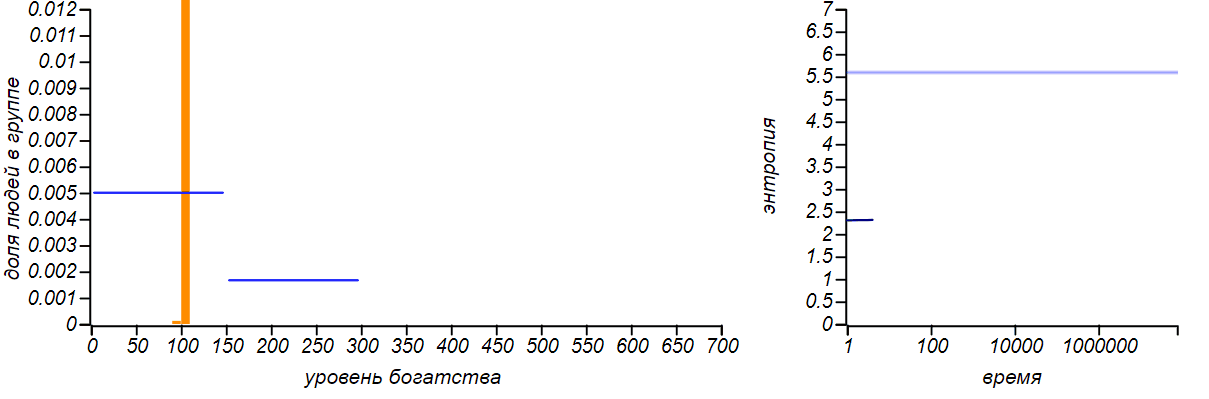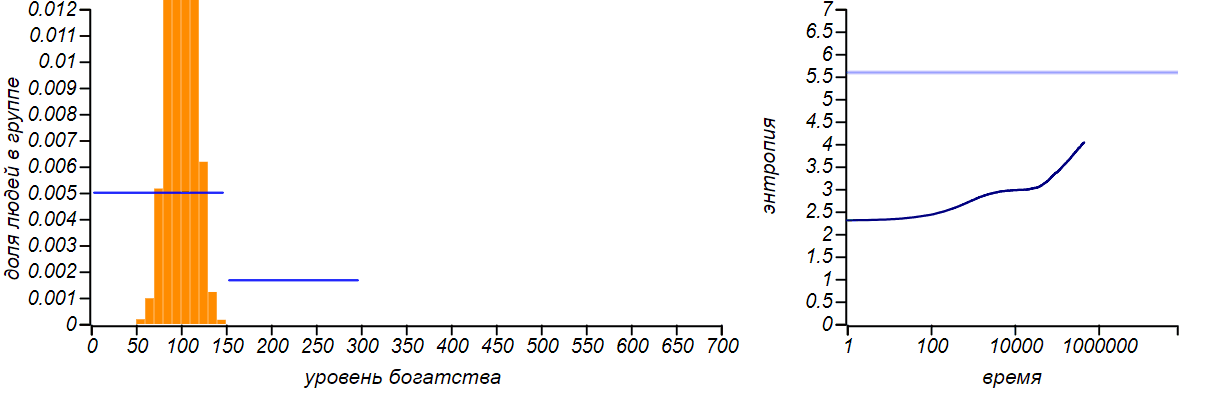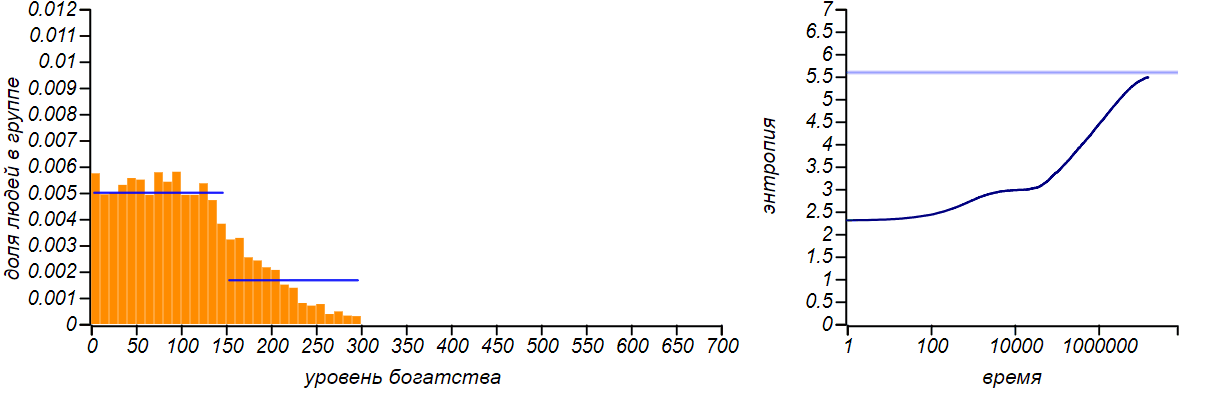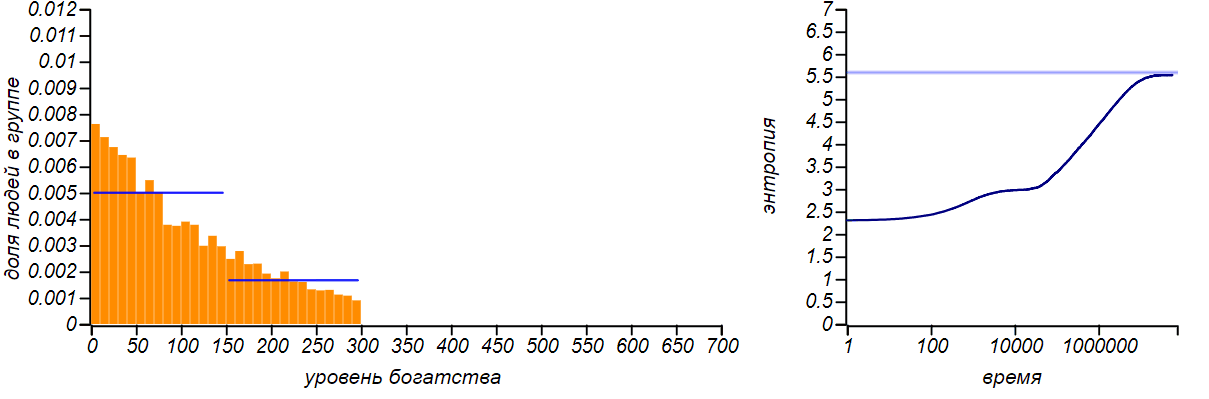 <\ br>
<\ br>
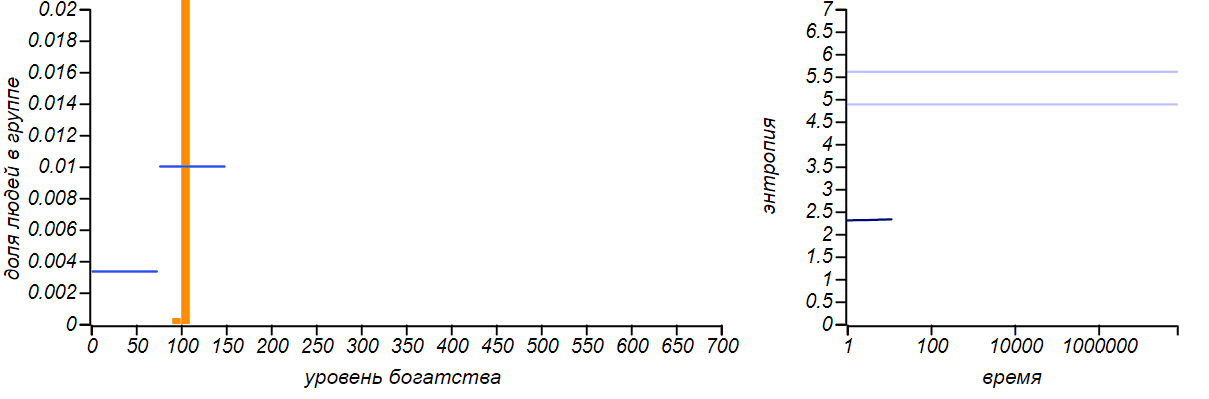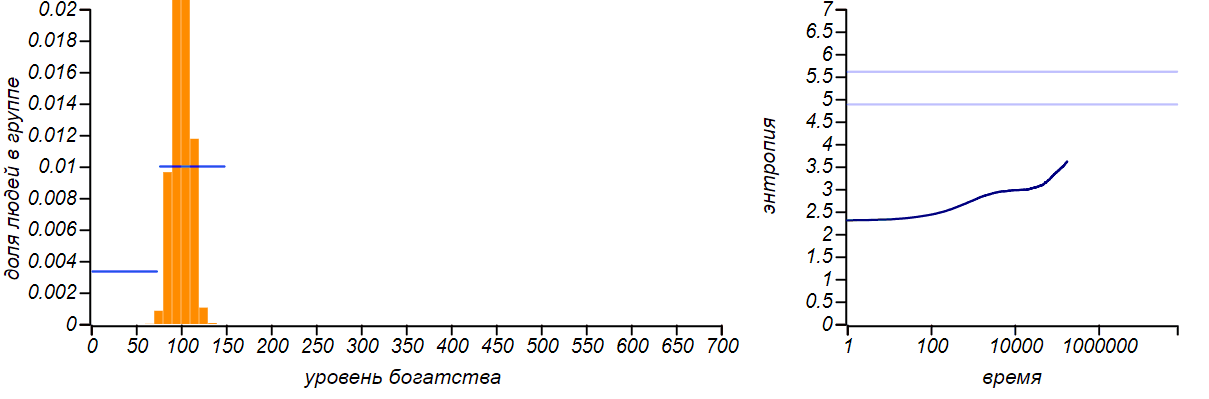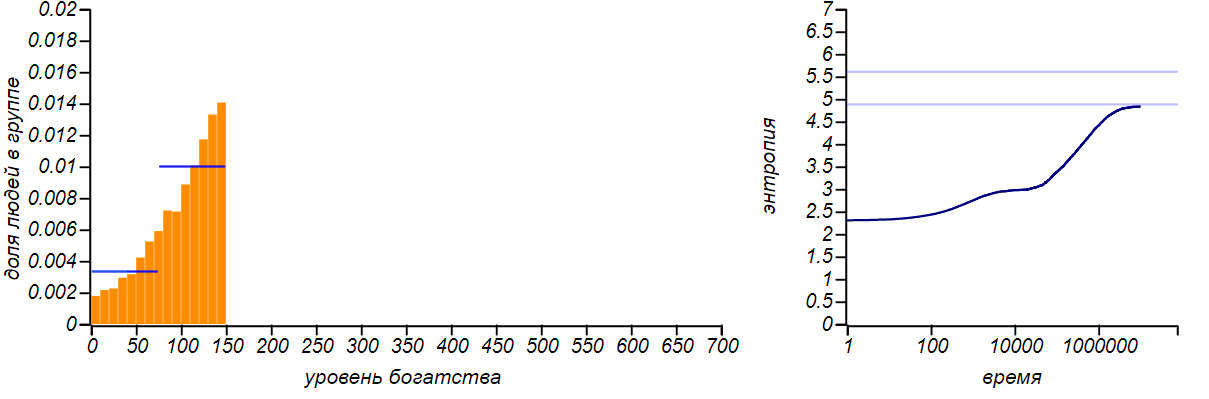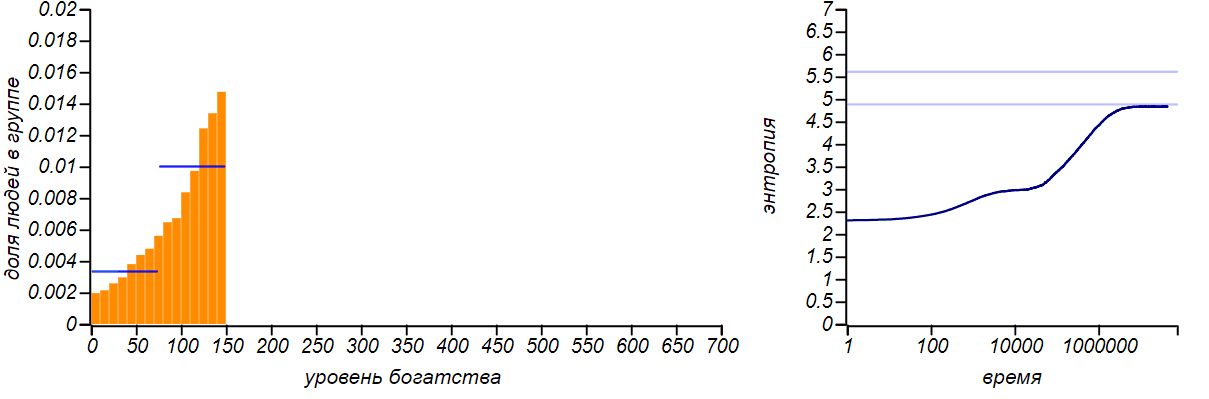
Variants of asymmetrical bounded distributions in comparison with Bernoulli distributions corresponding to a shift in the mean value. The horizontal lines in the entropy plots indicate theoretical values for the entropy of the Bernoulli distributions.
The distribution of wealth ceased to be uniform, taking the form of a limited exponential. With the shift of the right border to the left in equilibrium rich players became more than the poor. If we “chop up” the histogram, leaving only two columns, we get the Bernoulli distribution, which shows how likely it is to be conditionally “poor” or “rich”. When the values of a random variable are limited to only two values, the Bernoulli distribution is the only choice, and it naturally delivers the maximum entropy. But pay attention to the fact that the entropy of our model distributions tends to those values that are predicted by the Bernoulli distribution. The Gini coefficients for these two cases are equal.0.43 and 0.2 , respectively.
Mysterious and powerful entropy is, of course, cool and maybe even convincing. But why, with a symmetrical exchange, the poor become more than the rich? Why is the equilibrium mode zero? It is necessary, as physicists say, to understand the kinetics of the process, that is, the fate of individual particles. We were not mistaken in assuming that the random walk model describes the change in the state of an individual bidder: he is equally likely to take steps both up and down. And for a random walk, one famous law of meanness is executed: the curse of the player. Let me remind you that it consists in the fact that with a sufficiently long observation, a randomly wandering particle will necessarily end up in any place indicated in advance.Moreover, the distance at which the particle moves away from any starting point is proportional to the square root of the number of steps. All this leads to the fact that if a particle starts its path near zero, then it will reach it with a high probability, and since the zero in our problem is an impenetrable boundary, then it will be forced to again and again begin its path near the zero point, testing the notorious curse. As the particle moves away from zero, the probability of it returning decreases and the rich become more likely to save their state. But then what prevents the particle from moving away as far as it pleases, and for a particular player to become as rich as you like? In fact, nothing but the finiteness of money in the system - the exponential distribution differs from zero on the whole positive semiaxis.But in order to achieve incredible wealth according to the rules of our game, it is necessary that all players randomly choose the same player over and over again. And for the first time, the probability of such a choice is( 1 / n ) n - 1 - one billionth for a group of ten people, and it is incredible to repeat this many times. The choice of who to give money in our model falls on everyone in the same way, which means that he will not only get rich, but also poor. There is justice in this world! Though triumphant not for long, if you are not rich.
As long as our exchange model does not take into account the wealth of players, it remains unrealistic. In fact, the rich spend more and the poor less, moreover, intelligent people try to save some of their wealth. As the next complication of the model, let's demand that the players give some known share in the exchange.α of your condition. A new parameter and a new constraint are introduced into the system; therefore, the equilibrium state may deviate from the exponential one. Operating with shares on the level of welfare, we turn to multiplicative characteristics, such as, for example, return on investment, return on investment, etc. In all textbooks on economics it is indicated that if you want to calculate the average return on investment, say, for many years, you should calculate the geometric average for the returns of each year. In our case, the geometric mean is uniquely, although nontrivially, determined by the valueα .Thus, adding a new parameter, we fix the geometric mean of the distribution of players' income, or the average yield of the market model. So, we can expect that the equilibrium distribution of wealth should be well described by the gamma distribution. We can be sure of this by conducting a simulation.

If the exchange costs are proportional to the prosperity, the equilibrium distribution tends to a characteristic asymmetric bell-shaped gamma distribution. In this model α = 1 / 3 . The average exchange rate was 75 % .
The decrease in the share of the poor is due to the fact that they spend on average less than they receive from the rich, because both those and others exchange shares of their capital. But this social elevator is only valid whenα < 1 / 2 .If you spend more than half of what you have, the probability of being in the poor becomes very tangible. For different meaningsα can be obtained very different in form of distribution with a wide range of injustices:
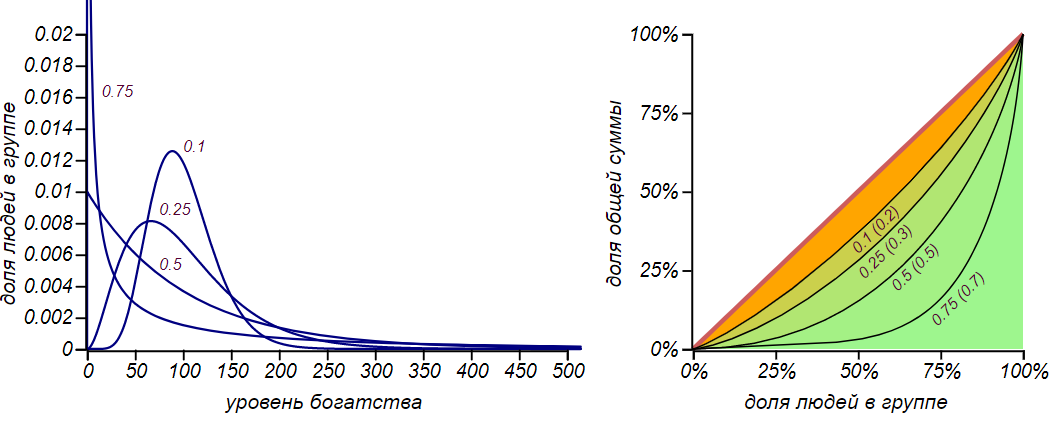
Various variants of equilibrium distributions at the expenses proportional to prosperity. Charts are marked with values. α , and the right graph in parentheses also shows the Gini index values.
It can be seen that the more of their capital players are forced to spend (for example, on daily needs or food), the greater the proportion of the poor and the less fair the society becomes. It is curious that whenα = 1 / 2 equilibrium becomes exponential distribution, both in the model with an equal exchange. The exponential distribution is a special case of the gamma distribution, so this transformation, in itself, is not surprising. But there is one curious subtlety: the entropy of this particular case is greater than the entropy of distributions with any other values.α . See how the entropy changes as the situation evolves α = 0.75 :
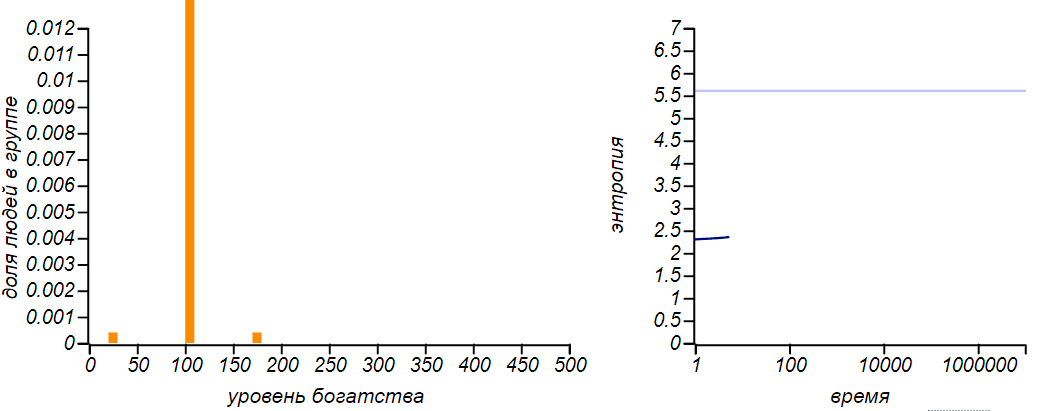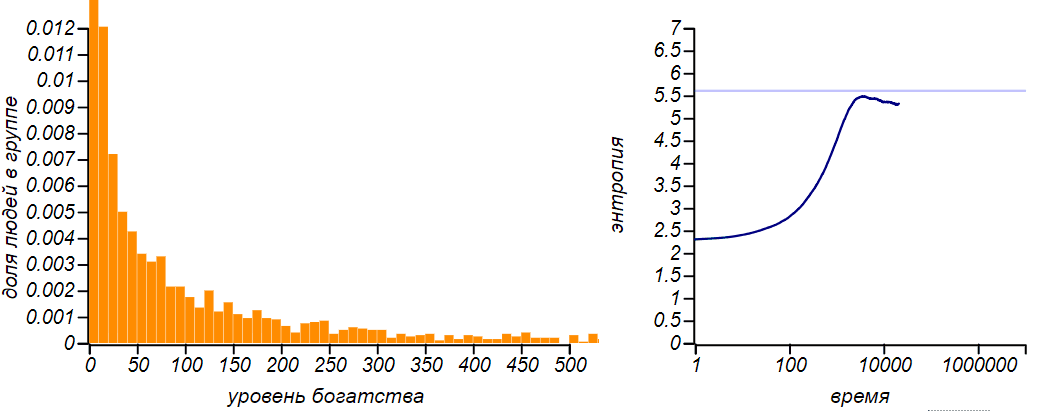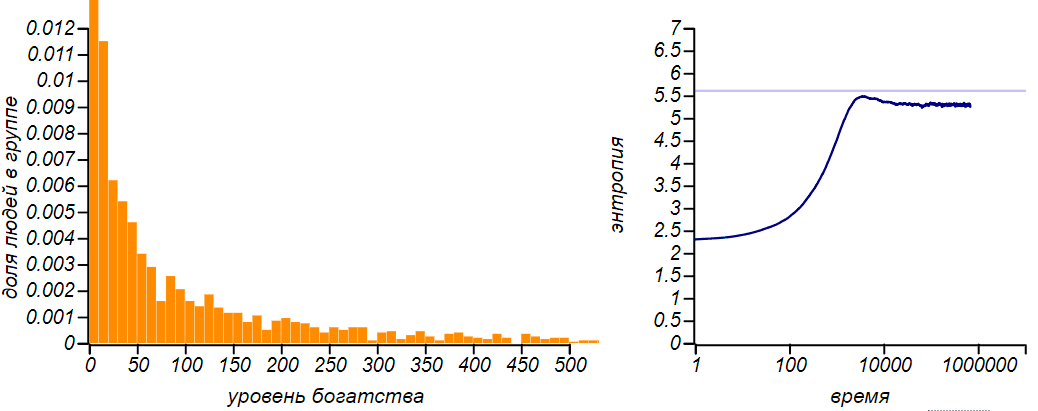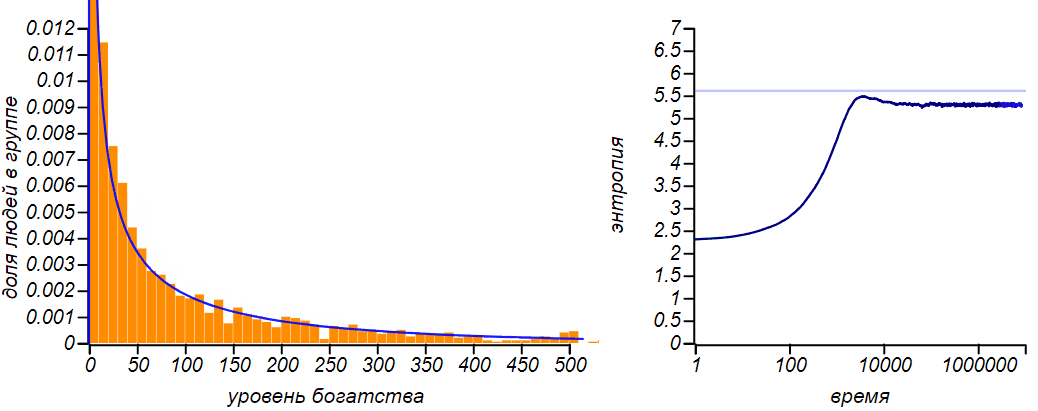 In the process of transition to equilibrium, the system "slips" the state with maximum entropy.
In the process of transition to equilibrium, the system "slips" the state with maximum entropy.
At first, the value of entropy monotonously increases, then, not reaching a theoretical maximum, a little, corresponding to the exponential distribution, it stops and begins to decrease. Does this not contradict the definition of an equilibrium state, as a state with a maximum of entropy? There is no contradiction, since the equilibrium state must be stationary, that is, not creating directed energy flows and stable, or, in the language of the theory of dynamic systems, attracting the system to itself. And of all the stationary equilibrium will be the state with maximum entropy. And in our caseα = 0.75 , the exponential distribution corresponds to the non-stationary state.Researchers from the University of Boston Ispolatov and Krapivsky have complicated the model of proportional exchange in such a way that the exchange takes into account not only the welfare of the spending, but also the recipient. A millionaire rarely buys something from a greengrocer, and a greengrocer rarely has a large income, on the other hand, the manufacturer of extra-class cars will only interact with rich customers, but he himself will not remain in the investment. And so, in models in which the rich start paying mostly to the rich, and the poor to the poor, society collapses completely.
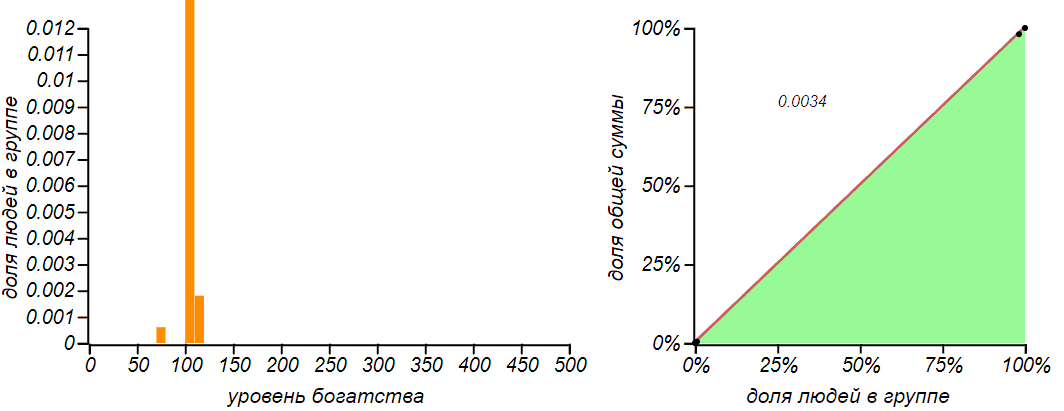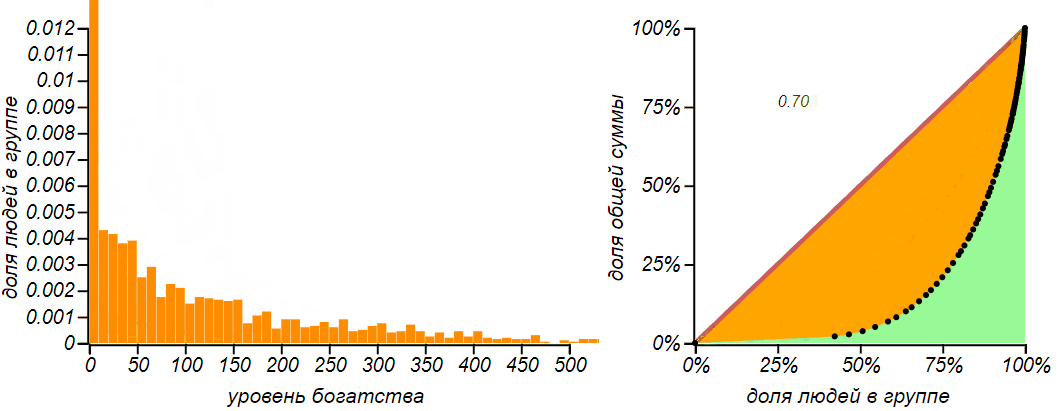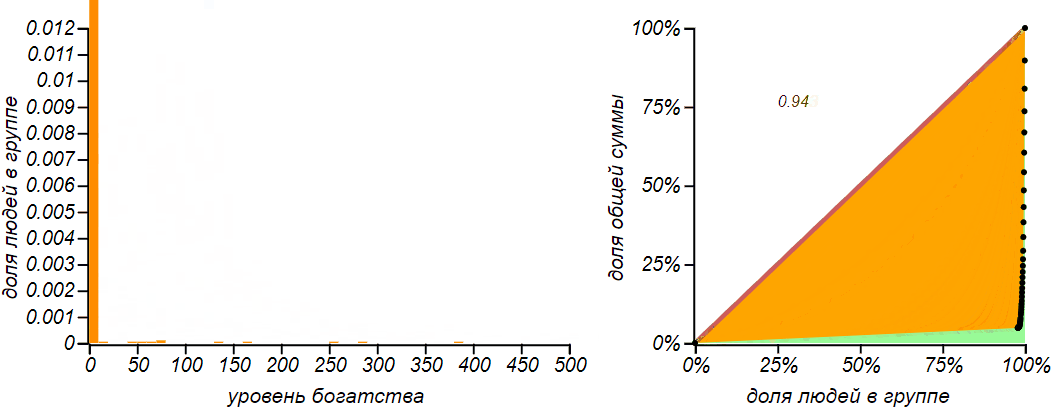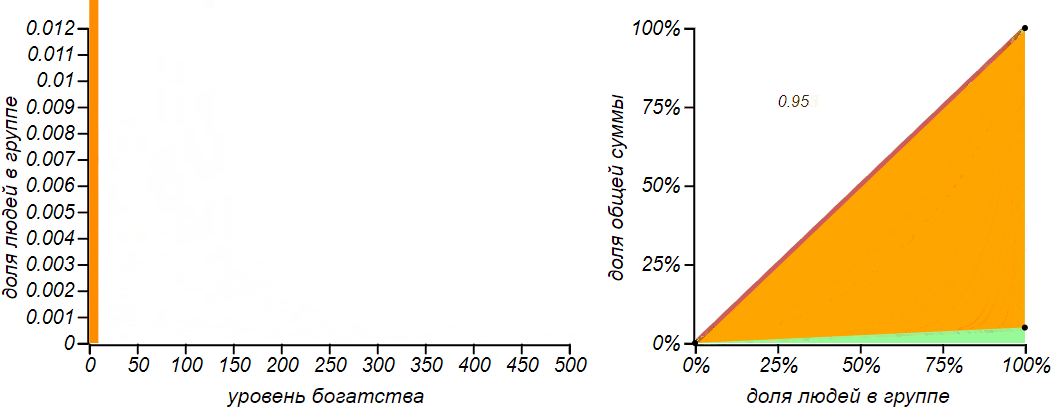
, . α=0.3,β=0.1 (. ).
In this system, there is only one stationary state: when all the players do not have (and therefore do not receive) absolutely nothing, and all the wealth goes to someone alone. The Gini coefficient in such a state is almost equal to unity, and it is very far from the normal equilibrium — its entropy is almost zero. Save the situation can limit the bottom, prohibiting players to lose absolutely all savings, in which case the equilibrium distribution again becomes exponential or gamma-shaped. You can also enter a restriction from above - then we get a certain asymmetric distribution corresponding to the Bernoulli distribution. The model of such a wild market is quite applicable to the securities market without any restrictions, but they are struggling with on real exchanges, imposing restrictions on the volume of transactions,committed per day and at maximum levels of growth or fall in the price of an asset.
All these are sad conclusions, which speak not in favor of the free market, or the matter, the model proposed by Sharikov! And what is the entropy of a degenerate distribution? According to the standard formula, it is exactly zero. This is the most nonequilibrium, the most unlikely distribution, and in any exchange model it is non-stationary, so such a society can only be obtained artificially. The wild market, of course, is not a gift - it is unstable and causes blatant inequality. Many mutually agreed restrictions and finely tuned connections are required to build a sustainable market and a more or less just society. Humanity is exploring this issue is not very long and basically, to the touch, by trial and error, but one thing is clear: injustice in the economic space is not a consequence of rotten human nature, but an objective feature of the system,part of which we are all. Moreover, attempts to create absolute justice in a ball-like manner always took place with battle and blood, and the results, by virtue of its disequilibrium, did not exist for long.
It is unlikely that molecules and atoms argue about the injustice of their world, and physicists and engineers for two hundred years have come to terms with the fact that whatever ideal heat engine they have built, chaos will not allow to convert heat into work of more than a fair share. When it is clear, it is not so insulting. I hope this chapter will help the curious reader to understand and accept our complex unjust world.
Published chapters:
In this chapter, we will discuss money, markets, and entropy, as well as look at animated gifs, which, alas, cannot be printed in a booklet.
')

Hongren's observation:The economy is a big, serious, but peculiar science. Undoubtedly, it is vital, as a discipline that studies the real and important phenomenon of our world: economic reality. Economics strives for provability and formalization; there is a lot of mathematics in it, sometimes complex and interesting. However, opening a serious economic textbook, you will most likely find some relatively simple calculations, ready-made recipes and a bunch of informal reasoning in this spirit: “but in reality everything may be wrong and, in general, somehow, the will of key players or government. " In the end, there may be a feeling that intuition, knowledge of psychology and the ability to perceive the general context are more important in this discipline than accurate calculation and meticulous consideration of details (it’s about economics, not accounting). Finally, almost half of fake dissertations are written precisely on economics, therefore, it is not too difficult to speculate on economic topics in a scientific manner. Let us try our strength in this field, thankfully, the injustice of this world is nowhere more acutely perceived as in the matter of the distribution of wealth. In addition, whatever a person is engaged in, whatever profession he may be in, he is involved in the economy and its games, from the laws of economics, just as he cannot hide from the laws of physics.
Among economists, the real world is often considered a special case.
Of the whole mass of problems solved by mathematical economics, we consider only one - how does it turn out that even under equal conditions for all market participants and a fair exchange of funds the poor become more than rich and why even an ideal mathematical society is prone to financial inequality. Well, in passing, we learn something curious about mathematical statistics and the distribution of random variables.
I am a physicist by education and by profession, and my professional deformation is expressed in a peculiar view of the world, as on a wide variety of physical systems and processes. From the point of view of physics, the real market is a substantially non-stationary open system, with many degrees of freedom, in which stochastic (random) processes play an important role. In this sense, the market is similar to the subject of studying such areas of physics as thermodynamics and statistical physics, in which, due to the inability to consider all the innumerable details and the behavior of all components of the system, go to its generalizing and measurable properties, such as energy, temperature or pressure . It is not surprising that attempts at a thermodynamic description of economic systems and the creation of econophysics have been made for more than a hundred years. But the trouble is: while scientists are examining the details, summarizing the knowledge gained and leading disputes about fundamental laws, the main object of study is economic reality, it has time to change beyond recognition. Her behavior seems to be trying to preserve, or even increase, her uncertainty and unpredictability.
A good example is the two-century history of using technical analysis when playing on the stock exchange. When a new powerful tool appears that allows you to grope hidden patterns and predict the course of a security or stock, it begins to bring profit to those who use it. But soon the market begins to “feel” new players and adapt to their strategy, the accuracy of predictions of the remarkable method begins to fall and, after some time, it falls into a large list of outdated and not very reliable tools. Neither modern flexible self-learning neural network algorithms, nor ultrafast robots-traders who perform millions of operations per minute, have not changed over the past two decades the main feature of the exchange game - its unpredictability. And until now, the main advantages of a professional in this industry are will, endurance of character, reluctance to excitement ... well, or possession of the exchange. Just like in a casino, where games are based on pure chance! On the one hand, this, of course, is insulting, but on the other - it gives reason to constantly improve methods and approaches. At one time, both the theory of probability and mathematical statistics were born from attempts to analyze gambling and economic games and only then found application in almost all natural sciences.
In further discussion, we will talk about money, but this familiar everyday-used category is surprisingly complex and ambiguous. The meaning and value of money depends on many factors, and by calling a certain amount of money out of context, we don’t say anything about its real value. This distinguishes monetary values from the majority of physical quantities that describe our world and makes it difficult to carry out rigorous arguments in the economy. But the purpose of our conversation: the mathematical foundations of the laws of meanness, everyday, clear and simple. Therefore, in the future, we will talk about certain “rubles”, meaning a formal ticket or a coin, and implying that the more these “rubles” are in someone, the “richer” they are. Other reasoning about the purchasing power, intangible or illiquid values, about "happiness is not in money", finally, we leave beyond the scope of the conversation.
Come on, enough for everyone!
We begin with an analysis of the validity of some simple distribution strategies of a known amount of money to a finite group of people.
The first, most obvious strategy: “take everything, and divide”, that is, allocate each member of the group for an equal share of the total amount. Such a distribution is called degenerate , it has a Gini index equal to zero and corresponds to the equality curve on the Lorentz diagram.

Absolutely fair degenerate distribution of money: everyone has everything equally.
Great option! Let's call it “Sharikov's strategy” in honor of the hero of the story of Mikhail Bulgakov “The Heart of a Dog”, who offered to solve all economic issues in this way.
The second, more realistic strategy is to distribute one ruble at random to each one. Who as lucky. We can call this strategy "Poisson" , since it is in this way that independent random events in the Poisson process are distributed on a time scale. For a group of n a person the probability of each of the participants to receive the ruble is 1 / n . After the distribution in this way M rubles, everyone should receive an amount equal to the number of such "positive" outcomes. The probability function for such a sum is well known - it is a binomial distribution , like a bell, symmetrically scattering around the mean M / n . Usually they are introduced to him by the example of calculating the probability of receiving a specified amount by throwing dice. For large values M the binomial distribution becomes almost indistinguishable from the normal one. Let's see how it will change, as money is distributed, the distribution of money in a group and its fairness.

The result of the distribution of money according to the principle “to whom God will send” is the binomial distribution. The more money we distribute, the greater the value of the average and the spread, but the probability of not getting anything practically disappears.
Algorithm Poisson Strategy
Baseline :xsis an array ofnelements, filled with zeros,Mis the total amount of money in the system.M i <- 1 n xs[i] <- xs[i] + 1
This distribution, from the point of view of justice, looks very good, moreover, it becomes the fairer the more money we distribute to the public! Just great! It is a pity that society is not arranged and the rain of money does not pour on all of us equally.
For completeness, let's consider another simple artificial distribution of money - uniform . With this distribution, the poor will be as many as the rich.

Equal distribution does not mean that money is distributed evenly across all. With this distribution, the number of rich, poor and middle peasants is the same, but the money mainly belongs to the rich.
Algorithm of the strategy of uniform distribution
Baseline :xsis an array ofnelements, filled with zeros,Mis the total amount of money in the system.x xs x <- 0 M/n
For a uniform distribution, the Lorenz curve is a quadratic parabola, and if the left boundary of the distribution is zero, then this parabola is independent of the position of the right boundary, and the Gini index for all such distributions is exactly 1 / 3 . Such an index value (but not such a distribution!) Was, for example, in the Australian economy in the 2000s - this is quite a good indicator.
However, the market is the market! The distributions discussed above are good, but require special conditions for their occurrence. If you give people the will to exchange money, change money for services, save them and squander in one night, the ideal distributions will lose stability and turn into some others.
New economic policy!
Consider a group of n person. As a result of the revolution, we will distribute to all participants in the experiment at an equal amount of money - according to m rubles each, having received the most fair Sharikovskiy distribution of funds in society. Now we give them the freedom to get rich and get poorer by the will of their own destiny and build a primitive model of the market. We will ask someone randomly selected to give one ruble to any person in the group who was also chosen randomly. We say that this is the purchase of a certain service at a fixed price. The distribution of wealth is expected to change: someone will have less money, someone more. We will repeat the exchange procedure again and again and take a look at how the distribution of wealth in the group will change.
It is reasonable to think before the experiment, what we expect to see. The exchange of money between the participants is equally likely, as in the case of the Poisson strategy of distributing money, but at the same time the players lose money, moreover, by the same Poisson principle and with the same intensity. Thus, it can be assumed that both positive and negative increments will be normally distributed and arranged symmetrically with respect to zero. Each player, in the end, will receive the difference of these increments, which for two normally distributed random variables will also be normally distributed, in this case, around zero, since losses and gains are symmetrical.

After a multitude of exchanges, each player will receive and lose an amount subordinate to a distribution close to normal. Total income will also be normally distributed around zero.
Thus, we get the classical random walk with normally distributed increments and we can expect some diffusion of means around the mean value m . The probability function should be blurred, increasing the variance with a constant average. It seems to be simple.
But there is a nuance. If, for some reason, someone from the group has no funds left, he will not be able to acquire services, giving money, but at the same time, can receive them. The possible value of welfare is limited to the left by zero, which means that the diffusion of wealth cannot spread infinitely and the observed probability function, sooner or later, will cease to be symmetrical.
There is another nuance. The amount of money in our closed system is limited and invariably, which means that random walks are not independent. Some lucky player will be able to get very large sums and get away from the ensemble very far, but only if the total mass is poorer. The participants in the experiment, using an invisible network, conserve the law of saving money in the system. What will the distribution of money in such conditions seek? It seems that the answer is not as obvious as it might seem at first glance, let's turn to simulation modeling and see what happens.

The result of simulation for the exchange of equal amount of money for n = 1000 and m = 100 . At first, a diffusion-like phenomenon is indeed observed, but as the probability function reaches the left boundary, the distribution tends to a characteristic asymmetric and not very fair form with a Gini coefficient close to 0.5 .
Equal Amount Exchange Algorithm
Initial data :xsis an array ofnelements, initialized with the values ofm.i <- 0 n xs[i] > 0 j <- 0 n xs[i] <- xs[i] - 1 xs[j] <- xs[j] + 1
If this book is read by a physicist, then he will be able to confidently assume that this may be for distribution, he will call it a Gibbs distribution. An attentive reader may recall that we have already met with a similar picture and with such a Gini index, when we considered frustration while waiting for a bus. Then we considered the distribution of intervals between Poisson events, which was described by an exponential distribution. Both of these shrewd gentlemen will be right in calling the same remarkably distribution with different names.
People - Molecules
Gibbs distribution is from the field of statistical physics. It describes the properties of systems, called the beautiful word "ensemble", which consist of a great number of interacting elements, most often particles. In an ensemble, you can select arbitrary subsystems (for example, individual particles or their groups) and assign certain state functions to them (these can be generalized coordinates, velocities, concentrations, chemical potentials, and much more). Using the methods of statistical physics, it is possible to explain and calculate the parameters of a wide variety of phenomena: chemical and catalytic processes, turbulence, ferromagnetism, the behavior of liquid crystals, superfluidity and superconductivity, and many others.
Gibbs distribution answers the question: what is the probability to meet a certain state of the subsystem, if given a) state energy, b) macroscopic (relatively speaking, global) properties of the system, such as temperature and c) it is known that the system is in thermodynamic equilibrium? It can be schematically expressed as follows:
p m a t h r m G i b b s ( T ) ( x ) = C e - f r a c E ( x ) k T ,
Where x - a certain state of the subsystem, E ( x ) - the energy of this state, T - the absolute temperature of the system (or its equivalent), and C and k - the values required for normalization and dimensional compliance. The equilibrium condition is very important, it means that time disappears from consideration and that the whole system will be in its most probable state for the given conditions.
The rigorous derivation of the expression for the Gibbs distribution is not needed here; instead, I want to show a beautiful purely mathematical argument leading to its exponential form. Since parts of a system are considered that give the whole system together, then as their characteristic it is worth choosing some additive value, that is, such that its value for the ensemble is the arithmetic sum of the values of its parts. Energy can be used as such in mechanics. On the other hand, we calculate the probability to observe a certain state of the system, and the probability is multiplicative , that is, if the system can be divided into parts, then the probability to observe all these parts will be equal to the product of the probabilities for the state of each of the parts. Thus, we need a function that turns an additive value into a multiplicative one. Only exponential function has this property. a x , the sum of the arguments turns into the product of the values: ax+y=axay. Well, of all the exponential functions, the exponential is the most convenient, since it behaves very well during integration and differentiation.
In our market model, we have an additive value - the amount of money each player has, it is an analogue of energy. With the exchange described by us, this quantity, like the energy in the physical system, is conserved. And what's the point here at the temperature? It's easy to figure out by looking at the expression for the probability density of the exponential distribution:
p mathrmExp( lambda)(x)= lambdae− lambdax,
and remembering that the mean for him is equal 1/ lambda . Since the number of players in the course of trading is unchanged, the average arithmetic amount of money from the players, equal to the amount initially distributed m . It naturally follows that lambda=1/m , it means that the average amount of money of the players is in the role of temperature in our economic model. In a “heated” market with great liquidity, we can observe a greater variation in wealth than in a “cold” one, because in the exponential distribution the dispersion is 1/ lambda2 . In the words of Ostap Bender in the “Golden Calf” by I. Ilf and E. Petrov: “Once any bank notes are roaming in the country, then there must be people who have a lot of them.”
If to be completely accurate, and remember that money in our experiment is a discrete value, then we observe a geometric distribution - a discrete analog of the exponential. It is found in the task of counting the number of failures before the first win when throwing coins of varying degrees of honesty. These two distributions are similar and become indistinguishable with decreasing probability of winning. In our experiment, the chances of getting a ruble are equal 1/1000 , it is small enough to call the distribution exponential.
It remains to deal with the equilibrium of the final state of the market. Thermodynamic equilibrium can be described in different ways. First, the steady state must be in equilibrium , in which the system can be indefinitely long, without changing its macroscopic parameters, and not forming within itself ordered flows of matter and energy. Secondly, it must be sustainable , that is, if the system is out of balance, it will tend to return to it. Thirdly, this is the most probable state of the system, most often observed, which the system will eventually seek to get from any other, non-equilibrium one. Our experiment demonstrates these equilibrium criteria: having come to an exponential distribution, the system remains in it, moreover, it is easy to make sure in the experiment that from any arbitrary distribution we, after some time, will again come to the exponential. But this is not proof, but only a hint that we are most likely dealing with equilibrium. We need some kind of formal measurable criterion, which would unequivocally indicate to us that the system is in equilibrium without having to wait indefinitely or sort through all possible initial distributions. This would be a useful criterion that could be applied to the real market, without the need to conduct risky experiments on living people.
Tao words - is not true Tao
Reflections on equilibrium led physicists to the concept of entropy , which gradually went beyond thermodynamics and so liked scientists of all directions, philosophers and the general public that now entropy got an aura of mystery, incomprehensibility and God knows what else. A simple and special, in essence, the concept has gained in the minds of the broad masses a reputation as an inexplicable concept controlling the world. This is due to the fact that thermodynamics is a universal science that describes at a very high level the abstractions of a system of the most diverse nature: from physical, chemical and biological to social, economic and even purely humanitarian. After the school course, however, there is a feeling that thermodynamics is about a boring perfect gas, some kind of pistons and an impossible Carnot cycle. Such a very one-sided presentation is connected with the remarkable fact that thermodynamics, being one of the most abstract and universal branches of natural science, elegantly solves applied problems that are understandable to schoolchildren and are useful in industry. This cannot be said, for example, of category theory or topology — also very abstract, universal and, undoubtedly, useful disciplines, but in everyday tasks almost never encountered.
So entropy. The creator of thermodynamics, Clausius, and later Gibbs and Boltzmann, required a quantitative characteristic of equilibrium, which speaks of the probability of observing the indicated state of the system or its parts. Moreover, this quantity, reflecting the probability, multiplicative in nature, must be an additive state function, so that it can be calculated for the system, adding the values calculated for its parts. When we were looking for a suitable function for the Gibbs distribution, we proceeded from the fact that it should turn an additive argument into a multiplicative value. When searching for an expression for entropy, we need a function that is multiplicative in argument and additive in value — this is the logarithmic function, the inverse of the exponential. The entropy of the state of a complex system can be expressed as the expected value for the logarithm of the probability of observing the state of all its parts, or, according to Boltzmann, as the logarithm of the number of ways in which this state of the system can be realized. In this case, a more probable state corresponds to a higher value of entropy, and to an equilibrium state, the maximum possible one.
The number of ways to implement a particular state depends on the number of restrictions or conditions under which this state can be realized. The fewer such restrictions, the more probable the state is and the greater the value of its entropy. These restrictions and conditions make sense of the status information . Hence the idea that entropy reflects the degree of our ignorance about the system: the less we know about the state, the greater its entropy. Later, Shannon summarized this concept for any systems containing information, including the distributions of random variables. Here is what he did: for a random variable X determined by the probability function p(x) entropy is defined as follows:
H(X) equiv− mathrmM( ln(p(x)))=− sump(x) ln(p(x)),
where summation is done over all values x , in which p(x)>0 . Thus, we have the opportunity to calculate the entropy of the state of any complex system, having its statistical description.
This is how entropy changes as our market model comes to equilibrium.

Entropy growth as the market approaches equilibrium. The horizontal line in the right graph shows the theoretical value of the entropy for the exponential distribution, equal to 1− ln( lambda) . The intermediate “shelf” corresponds to the period during which the distribution passed through the diffusion stage and was similar to the normal one.
Thus, to each distribution: given analytically or experimentally obtained in the form of a histogram, you can put in correspondence a positive number - its entropy. This means that the distributions can be compared with each other, determining more or less equilibrium and probable for given conditions. Moreover, for a certain class of distributions it is possible to distinguish a distribution with maximum entropy, and, moreover, only one. Classes are determined by constraints, or a measure of our knowledge of the statistical properties of a system. Here are some examples:
| what we know about the random variable X | entropy distributions |
|---|---|
| X in[a,b] | uniform on the segment [a,b] |
| X \ in \ {0,1 \}X \ in \ {0,1 \} | Bernoulli distribution |
| X in[0, infty) + average | exponential, for a discrete quantity - geometric |
| X in[xm, infty) + geometric mean | Pareto distribution (power) |
| X in[0, infty) + mean + geometric mean | gamma distribution |
| X in[0, infty) + geometric mean + variance for geometric mean | log normal |
| X in(− infty, infty) + average + variance | normal |
All familiar faces! These are very often used distributions that statistics apply to the widest class of problems. Their universality is due precisely to the fact that they, having the maximum entropy, are most likely and observable. Many distributions of real random variables aspire to them as equilibrium. The most free of restrictions among all others is the normal distribution: it requires a minimum of information about the random variable. Less is no longer possible: if we indicate only the mean value, then in an effort to increase entropy, the distribution will be “spread out” along the entire numerical axis.But, if we know only the mean value, but at the same time we restrict the random value to positive values, then the equilibrium distribution will be unambiguous - exponential. This is the case that we observed in our experiment with the market. We knew in advance only how much money we gave to each player and the fact that the amount of money in the system was constant, it fixed the average value. And since the money we have is a positive value, most likely in equilibrium we will get an exponential distribution of wealth with a Gini index equal1 / 2 .
There are many modifications of the model described by us: the exchange can take place not by one ruble, but by a random variable, limited by the state of the giver, while you can give money not to any one player, but distribute it randomly. Until we introduce new parameters into the game, all these modifications do not change the form of the equilibrium distribution of wealth - it remains exponential. You can make sure of this with the help of simulation modeling, but it’s not interesting to provide pictures for various exchange methods - they are all the same. Many researchers have noted this feature of market models. An interesting model is built by Dragulescu and Yakovenko from the University of Maryland, in which players are united into certain companies and further simulated is the interaction of companies with employee-players and buyers-players.But even in this complex case, the exponential distribution is indifferent, indifferent to the model parameters chosen.
To demonstrate the universality of the principle of maximum entropy, let us artificially limit the level of an individual player’s wealth from above, forbidding him to receive money if he already has some fixed amount. The equilibrium distribution, of course, will change. And if the right border is equal to twice the average value, then we come to the case described in the first row of the table. Indeed, by limiting a random variable to a finite segment and not indicating anything more, we cannot assume any other expected value of the average, except the middle of this segment. Therefore, the equilibrium distribution in this case should be uniform. Let's check, is it?

This is what happens when the upper limit of the possible level of player wealth is limited, and, in such a way, that the upper limit is exactly twice the average value. According to the principle of maximum entropy, the equilibrium distribution should be uniform. The horizontal line on the right graph shows the theoretical value of entropy for uniform distribution.
Equal Sum Exchange Algorithm with Top Limit
Initial data :xs- an array ofnelements, initialized by valuesm,xMax- the maximum amount allowed.i <- 0 n xs[i] > 0 j <- 0 n xs[j] < xMax xs[i] <- xs[i] - 1 xs[j] <- xs[j] + 1
And what will happen in case of symmetry breaking, that is, if we move the right border to the right or left?


Variants of asymmetrical bounded distributions in comparison with Bernoulli distributions corresponding to a shift in the mean value. The horizontal lines in the entropy plots indicate theoretical values for the entropy of the Bernoulli distributions.
The distribution of wealth ceased to be uniform, taking the form of a limited exponential. With the shift of the right border to the left in equilibrium rich players became more than the poor. If we “chop up” the histogram, leaving only two columns, we get the Bernoulli distribution, which shows how likely it is to be conditionally “poor” or “rich”. When the values of a random variable are limited to only two values, the Bernoulli distribution is the only choice, and it naturally delivers the maximum entropy. But pay attention to the fact that the entropy of our model distributions tends to those values that are predicted by the Bernoulli distribution. The Gini coefficients for these two cases are equal.0.43 and 0.2 , respectively.
Mysterious and powerful entropy is, of course, cool and maybe even convincing. But why, with a symmetrical exchange, the poor become more than the rich? Why is the equilibrium mode zero? It is necessary, as physicists say, to understand the kinetics of the process, that is, the fate of individual particles. We were not mistaken in assuming that the random walk model describes the change in the state of an individual bidder: he is equally likely to take steps both up and down. And for a random walk, one famous law of meanness is executed: the curse of the player. Let me remind you that it consists in the fact that with a sufficiently long observation, a randomly wandering particle will necessarily end up in any place indicated in advance.Moreover, the distance at which the particle moves away from any starting point is proportional to the square root of the number of steps. All this leads to the fact that if a particle starts its path near zero, then it will reach it with a high probability, and since the zero in our problem is an impenetrable boundary, then it will be forced to again and again begin its path near the zero point, testing the notorious curse. As the particle moves away from zero, the probability of it returning decreases and the rich become more likely to save their state. But then what prevents the particle from moving away as far as it pleases, and for a particular player to become as rich as you like? In fact, nothing but the finiteness of money in the system - the exponential distribution differs from zero on the whole positive semiaxis.But in order to achieve incredible wealth according to the rules of our game, it is necessary that all players randomly choose the same player over and over again. And for the first time, the probability of such a choice is( 1 / n ) n - 1 - one billionth for a group of ten people, and it is incredible to repeat this many times. The choice of who to give money in our model falls on everyone in the same way, which means that he will not only get rich, but also poor. There is justice in this world! Though triumphant not for long, if you are not rich.
The economy must be economical
As long as our exchange model does not take into account the wealth of players, it remains unrealistic. In fact, the rich spend more and the poor less, moreover, intelligent people try to save some of their wealth. As the next complication of the model, let's demand that the players give some known share in the exchange.α of your condition. A new parameter and a new constraint are introduced into the system; therefore, the equilibrium state may deviate from the exponential one. Operating with shares on the level of welfare, we turn to multiplicative characteristics, such as, for example, return on investment, return on investment, etc. In all textbooks on economics it is indicated that if you want to calculate the average return on investment, say, for many years, you should calculate the geometric average for the returns of each year. In our case, the geometric mean is uniquely, although nontrivially, determined by the valueα .Thus, adding a new parameter, we fix the geometric mean of the distribution of players' income, or the average yield of the market model. So, we can expect that the equilibrium distribution of wealth should be well described by the gamma distribution. We can be sure of this by conducting a simulation.

If the exchange costs are proportional to the prosperity, the equilibrium distribution tends to a characteristic asymmetric bell-shaped gamma distribution. In this model α = 1 / 3 . The average exchange rate was 75 % .
Algorithm of proportional exchange
Baseline :xs- an array ofnelements, initialized by valuesm,alpha- the share of capital that is spent during the exchange.i <- 0 n xs[i] > 0 dx <- floor(xs[i]*alpha) xs[i] <- xs[i] - dx j <- 0 n xs[j] <- xs[j] + dx
The decrease in the share of the poor is due to the fact that they spend on average less than they receive from the rich, because both those and others exchange shares of their capital. But this social elevator is only valid whenα < 1 / 2 .If you spend more than half of what you have, the probability of being in the poor becomes very tangible. For different meaningsα can be obtained very different in form of distribution with a wide range of injustices:

Various variants of equilibrium distributions at the expenses proportional to prosperity. Charts are marked with values. α , and the right graph in parentheses also shows the Gini index values.
Exact solution
, , . , , , , , , . , , , .
- Gamma(k,θ) — , , k=1 . , . , — . — , - , , -. ,
, :
- Gamma(k,θ) — , , k=1 . , . , — . — , - , , -. ,
X∼Gamma(k1,θ),Y∼Gamma(k2,θ)⟹X+Y∼Gamma(k1+k2,θ)
, :
X∼Gamma(k,θ)⟹aX∼Gamma(k,aθ).
m α : Gamma(1α−1,1m(1α−1)) .It can be seen that the more of their capital players are forced to spend (for example, on daily needs or food), the greater the proportion of the poor and the less fair the society becomes. It is curious that whenα = 1 / 2 equilibrium becomes exponential distribution, both in the model with an equal exchange. The exponential distribution is a special case of the gamma distribution, so this transformation, in itself, is not surprising. But there is one curious subtlety: the entropy of this particular case is greater than the entropy of distributions with any other values.α . See how the entropy changes as the situation evolves α = 0.75 :

At first, the value of entropy monotonously increases, then, not reaching a theoretical maximum, a little, corresponding to the exponential distribution, it stops and begins to decrease. Does this not contradict the definition of an equilibrium state, as a state with a maximum of entropy? There is no contradiction, since the equilibrium state must be stationary, that is, not creating directed energy flows and stable, or, in the language of the theory of dynamic systems, attracting the system to itself. And of all the stationary equilibrium will be the state with maximum entropy. And in our caseα = 0.75 , the exponential distribution corresponds to the non-stationary state.Researchers from the University of Boston Ispolatov and Krapivsky have complicated the model of proportional exchange in such a way that the exchange takes into account not only the welfare of the spending, but also the recipient. A millionaire rarely buys something from a greengrocer, and a greengrocer rarely has a large income, on the other hand, the manufacturer of extra-class cars will only interact with rich customers, but he himself will not remain in the investment. And so, in models in which the rich start paying mostly to the rich, and the poor to the poor, society collapses completely.

, . α=0.3,β=0.1 (. ).
-
:xs—n,m,alpha— , ,beta— , .i <- 0 n xs[i] > 0 dx <- floor(xs[i]*alpha) xs[i] <- xs[i] - dx dx > 0 j <- 0 n d = min(dx, floor(xs[j]*beta)) xs[j] <- xs[j] + d dx <- dx - d
In this system, there is only one stationary state: when all the players do not have (and therefore do not receive) absolutely nothing, and all the wealth goes to someone alone. The Gini coefficient in such a state is almost equal to unity, and it is very far from the normal equilibrium — its entropy is almost zero. Save the situation can limit the bottom, prohibiting players to lose absolutely all savings, in which case the equilibrium distribution again becomes exponential or gamma-shaped. You can also enter a restriction from above - then we get a certain asymmetric distribution corresponding to the Bernoulli distribution. The model of such a wild market is quite applicable to the securities market without any restrictions, but they are struggling with on real exchanges, imposing restrictions on the volume of transactions,committed per day and at maximum levels of growth or fall in the price of an asset.
All these are sad conclusions, which speak not in favor of the free market, or the matter, the model proposed by Sharikov! And what is the entropy of a degenerate distribution? According to the standard formula, it is exactly zero. This is the most nonequilibrium, the most unlikely distribution, and in any exchange model it is non-stationary, so such a society can only be obtained artificially. The wild market, of course, is not a gift - it is unstable and causes blatant inequality. Many mutually agreed restrictions and finely tuned connections are required to build a sustainable market and a more or less just society. Humanity is exploring this issue is not very long and basically, to the touch, by trial and error, but one thing is clear: injustice in the economic space is not a consequence of rotten human nature, but an objective feature of the system,part of which we are all. Moreover, attempts to create absolute justice in a ball-like manner always took place with battle and blood, and the results, by virtue of its disequilibrium, did not exist for long.
It is unlikely that molecules and atoms argue about the injustice of their world, and physicists and engineers for two hundred years have come to terms with the fact that whatever ideal heat engine they have built, chaos will not allow to convert heat into work of more than a fair share. When it is clear, it is not so insulting. I hope this chapter will help the curious reader to understand and accept our complex unjust world.
Source: https://habr.com/ru/post/424071/
All Articles