AI, practical course. Deep learning to generate music

This is the last article in a series of educational articles for developers in the field of artificial intelligence. It discusses steps to create a deep learning model for generating music, selecting the appropriate model and preprocessing data, and describes the procedures for setting, training, testing and modifying BachBot.

Music generation - thinking about the task

The first step in solving a set of problems using artificial intelligence (AI) is to reduce the problem to a basic problem, which is solved by means of AI. One such problem is sequence prediction, which is used in applications for translating and processing natural language. Our task of generating music can be reduced to the problem of predicting the sequence, while the prediction will be performed for a sequence of musical notes.

Model selection

There are several different types of neural networks that can be considered as a model: direct distribution neural networks, recurrent neural networks and neural networks with long short-term memory.
')
Neurons are basic abstract elements that combine to form neural networks. Essentially, a neuron is a function that accepts data at the input and outputs the result at the output.


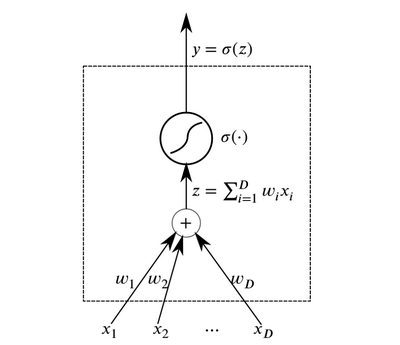
Neuron

Layers of neurons that accept the same data as input and have connected outputs can be combined to build a direct propagation neural network . Such neural networks demonstrate high results due to the composition of nonlinear activation functions when data passes through several layers (the so-called deep learning).


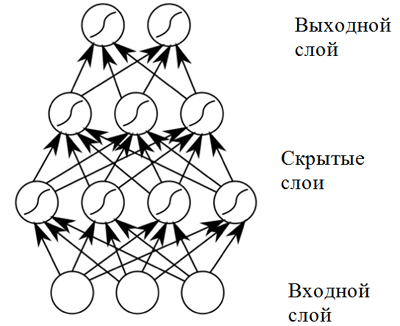
Direct distribution neural network

The direct propagation neural network shows good results in a wide range of applications. However, such a neural network has one drawback that does not allow its use in a task related to a musical composition (sequence prediction): it has a fixed dimensionality of the input data, and musical compositions may have different lengths. In addition, the forward propagation neural networks do not take into account the input data from previous time steps, which makes them not very useful for solving the sequence prediction problem! A model called a recurrent neural network is better suited for this task.

Recurrent neural networks solve both of these problems by introducing connections between hidden nodes: at the same time, in the next time step, nodes can get information about the data in the previous time step.


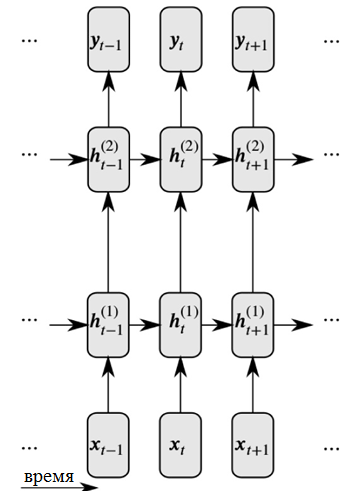
Expanded Recurrent Neural Network View

As you can see in the figure, each neuron now accepts input from both the previous neural layer and from the previous point in time.

Recurrent neural networks dealing with large input sequences encounter the so-called vanishing gradient problem : this means that the influence from the earlier time steps is quickly disappearing. This problem is characteristic of the task of a musical composition, since in music there are important long-term dependencies that must be taken into account.

To solve the problem of a vanishing gradient, a modification of a recurrent network called a neural network with a long short-term memory (or LSTM neural network) can be used . This problem is solved by the introduction of memory cells, which are carefully controlled by three types of "valves". Click the following link for more information: General information about LSTM neural networks .

Thus, BachBot uses a model based on an LSTM neural network.

Preliminary processing

Music is a very complex art form and includes various dimensions: the pitch of the sounds, rhythm, tempo, dynamic hues, articulation, and more. To simplify music for the purposes of this project , only the height and duration of the sounds are considered . Moreover, all chorals were transposed into the key in C major (C major) or A minor (A minor), and the duration of the notes were quantized in time (rounded) to the nearest value multiple of the sixteenth note. These actions were taken to reduce the complexity of the songs and improve network performance, while the basic music content remained unchanged. Operations on the normalization of the tonalities and durations of the notes were performed using the music21 library.

def standardize_key(score): """Converts into the key of C major or A minor. Adapted from https://gist.github.com/aldous-rey/68c6c43450517aa47474 """ # conversion tables: eg Ab -> C is up 4 semitones, D -> A is down 5 semitones majors = dict([("A-", 4),("A", 3),("B-", 2),("B", 1),("C", 0),("C#",-1), ("D-", -1),("D", -2),("E-", -3),("E", -4),("F", -5),("F#",6), ("G-", 6), ("G", 5)]) minors = dict([("A-", 1),("A", 0),("B-", -1),("B", -2),("C", -3),("C#",-4), ("D-", -4),("D", -5),("E-", 6),("E", 5),("F", 4),("F#",3), ("G-",3),("G", 2)]) # transpose score key = score.analyze('key') if key.mode == "major": halfSteps = majors[key.tonic.name] elif key.mode == "minor": halfSteps = minors[key.tonic.name] tScore = score.transpose(halfSteps) # transpose key signature for ks in tScore.flat.getKeySignatures(): ks.transpose(halfSteps, inPlace=True) return tScore 

The code used to standardize key characters in the collected works, the output uses C keys (C major) or A minor (A minor)

Quantization in time to the nearest value, multiple to the sixteenth note, was performed using the Stream.quantize () function of the music21 library. The following is a comparison of the statistics associated with the data set before and after its preliminary processing:


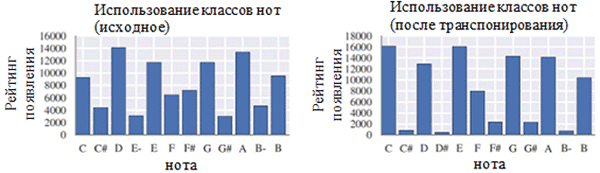
Use each note class before (left) and after preprocessing (right). The class of notes is a note regardless of its octave.


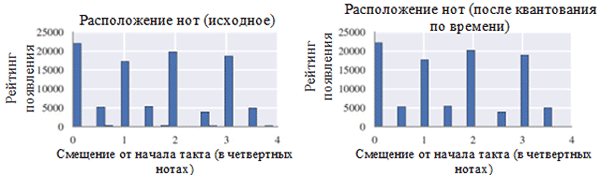
The location of the notes before (left) and after preprocessing (right)

As can be seen in the figure above, the transposition of the original tone of the chorals into the key in C major (C major) or A minor (A minor) significantly influenced the class of notes used in the collected works. In particular, the number of occurrences for notes in keys in C major (C major) and A minor (A minor) (C, D, E, F, G, A, B) increased. You can also observe small peaks for the F # and G # notes due to their presence in the ascending melodic A minor sequence (A, B, C, D, E, F # and G #). On the other hand, time-slicing had a much smaller effect. This can be explained by the high resolution of quantization (similar to rounding to a set of significant digits).

Coding

After the data has been pre-processed, it is necessary to encode the chorales in a format that can be easily processed using a recurrent neural network. The required format is a sequence of tokens . For the BachBot project, coding at the level of notes was chosen (each token represents a note) instead of the level of chords (each token represents a chord). This solution reduced the size of the dictionary from 128 ⁴ possible chords to 128 possible notes, which made it possible to increase the efficiency of work.

For the project BachBot was created the original coding scheme of musical compositions. The choral is broken down into temporary steps corresponding to the sixteenth notes. These steps are called frames. Each frame contains a sequence of tuples representing the pitch of a note in the format of a digital musical instrument interface (MIDI) and a sign of the binding of this note to a previous note of the same height (note, sign of binding). The notes within the frame are numbered in descending order of height (soprano → alto → tenor → bass). Each frame can also have a fermat indicating the end of a phrase; A fermat is represented by a dot symbol (.) above a note. The symbols START and END are added to the beginning and end of each choral. These symbols cause the initialization of the model and allow the user to determine the end of the composition.

START
(59, True)
(56, True)
(52, True)
(47, True)
|||
(59, True)
(56, True)
(52, True)
(47, True)
|||
(.)
(57, False)
(52, False)
(48, False)
(45, False)
|||
(.)
(57, True)
(52, True)
(48, True)
(45, True)
|||
END
An example of coding two chords. Each chord lasts the eighth beat, the second chord is accompanied by a fermata. The sequence "|||" denotes the end of the frame

 def encode_score(score, keep_fermatas=True, parts_to_mask=[]): """ Encodes a music21 score into a List of chords, where each chord is represented with a (Fermata :: Bool, List[(Note :: Integer, Tie :: Bool)]). If `keep_fermatas` is True, all `has_fermata`s will be False. All tokens from parts in `parts_to_mask` will have output tokens `BLANK_MASK_TXT`. Time is discretized such that each crotchet occupies `FRAMES_PER_CROTCHET` frames. """ encoded_score = [] for chord in (score .quantize((FRAMES_PER_CROTCHET,)) .chordify(addPartIdAsGroup=bool(parts_to_mask)) .flat .notesAndRests): # aggregate parts, remove markup # expand chord/rest st constant timestep between frames if chord.isRest: encoded_score.extend((int(chord.quarterLength * FRAMES_PER_CROTCHET)) * [[]]) else: has_fermata = (keep_fermatas) and any(map(lambda e: e.isClassOrSubclass(('Fermata',)), chord.expressions)) encoded_chord = [] # TODO: sorts Soprano, Bass, Alto, Tenor without breaking ties # c = chord.sortAscending() # sorted_notes = [c[-1], c[0]] + c[1:-1] # for note in sorted_notes: for note in chord: if parts_to_mask and note.pitch.groups[0] in parts_to_mask: encoded_chord.append(BLANK_MASK_TXT) else: has_tie = note.tie is not None and note.tie.type != 'start' encoded_chord.append((note.pitch.midi, has_tie)) encoded_score.append((has_fermata, encoded_chord)) # repeat pitches to expand chord into multiple frames # all repeated frames when expanding a chord should be tied encoded_score.extend((int(chord.quarterLength * FRAMES_PER_CROTCHET) - 1) * [ (has_fermata, map(lambda note: BLANK_MASK_TXT if note == BLANK_MASK_TXT else (note[0], True), encoded_chord)) ]) return encoded_score 

The code used to encode the music21 tone using a special coding scheme

Model setting

In the previous section, an explanation was given, showing that the task of automatic composition can be reduced to the task of predicting a sequence. In particular, the model can predict the most likely next note based on previous notes. For solving this type of problem, a neural network with long short-term memory (LSTM) is best suited. Formally, the model should predict P (x _{t + 1} | x _t , h _t-1 ), the probability distribution for the following possible notes (x _{t + 1} ) based on the current token (x _t ) and the previous hidden state (h _t-1 ) . Interestingly, the same operation is performed by language models based on recurrent neural networks.

In composition mode, the model is initialized using the START token, after which it selects the next most likely token to follow. After that, the model continues to select the next most likely token using the previous note and the previous hidden state until the END token is generated. The system contains temperature elements that add a certain degree of randomness to prevent BachBot from writing the same piece over and over again.

Loss function

When training a model for prediction, there is usually some function that needs to be minimized (called the loss function). This function describes the difference between the prediction model and the ground truth property. BachBot minimizes the loss of cross entropy between the predicted distribution (x _{t + 1} ) and the actual distribution of the objective function. Using cross entropy as a loss function is a good starting point for a wide range of tasks, but in some cases you can use your own loss function. Another permissible approach is to attempt to use various loss functions and apply the model that minimizes the actual loss during the audit.

Training / Testing

During the training of the recursive neural network, BachBot used token correction with x _{t + 1} instead of applying model prediction. This process, known as forced learning, is used to ensure convergence, since the predictions of the model will naturally produce poor results at the beginning of the training. On the contrary, during testing and composition, the model prediction x _{t + 1} should be reused as input to the next prediction.

Other considerations

To improve the efficiency in this model, the following practical methods common to LSTM neural networks were used: normalized gradient truncation, elimination method, packet normalization, and truncated back error propagation over time (BPTT).

The method of normalized gradient truncation eliminates the problem of uncontrolled growth of the gradient value (the inverse of the vanishing gradient problem, which was solved by using the LSTM-memory cell architecture). When using this technique, gradient values ​​that exceed a certain threshold are truncated or scaled.

The elimination method is a technique in which some neurons selected at random are turned off (excluded) during network training. This avoids over-fitting and improves the quality of generalization. The overfitting problem occurs when the model becomes optimized for the training data set and is less applicable for samples outside this set. The exclusion method often worsens the loss during training, but improves it during the verification phase (more on this below).

The calculation of the gradient in a recurrent neural network for a sequence of 1000 elements is equivalent in cost to the forward and backward passage in the neural network of forward propagation from 1000 layers. The truncated back-propagation error (BPTT) method over time is used to reduce the cost of updating the parameters in the learning process. This means that errors propagate only for a fixed number of time steps, counting back from the current moment. Note that long-term dependencies in learning are still possible with the BPTT method, since hidden states have already been manifested in many previous time steps.

Options

The following is a list of relevant parameters for models of recurrent neural networks / neural networks with long short-term memory:

• The number of layers . Increasing this parameter may increase the efficiency of the model, but it will take more time to train it. In addition, too many layers may lead to overfitting.
• The dimension of the hidden state . Increasing this parameter may increase the complexity of the model, but this may lead to oversubstituting.
• Dimension vector mappings
• The length of the sequence / number of frames before performing the truncation of back-propagation errors in time.
• The probability of exclusion of neurons . The probability with which a neuron will be excluded from the network at each update cycle.

The method of selecting the optimal set of parameters will be discussed later in this article.

Implementation, training and testing

Platform Selection

Currently, there are many platforms that allow you to implement machine learning models in various programming languages ​​(including even JavaScript!). Popular platforms include scikit-learn , TensorFlow and Torch .

The Torch library was chosen as the platform for the BachBot project. At first, the TensorFlow library was tried, but at that time it used deployed recurrent neural networks, which led to an overflow of the graphics processor's RAM. Torch is a scientific computing platform that runs on the fast programming language LuaJIT *. The Torch platform contains excellent libraries for working with neural networks and optimization.

Model implementation and training

The implementation will obviously vary depending on the language and platform on which you choose. To find out how BachBot implements neural networks with long short-term memory using Torch, check out the scripts used to train and set BachBot parameters. These scripts are available on the Feynman Liang GitHub website .

A good starting point for navigating the repository is the 1-train.zsh script . With it, you can find the path to the bachbot.py file.

More precisely, the main script for setting model parameters is the LSTM.lua file. The script for training the model is the train.lua file.

Hyperparameter Optimization

To search for optimal values ​​of hyperparameters, we used the grid search method using the following parameter grid.


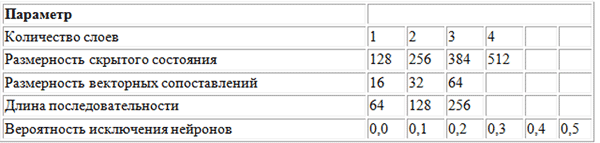
The grid of parameters used by BachBot when searching on the grid

The grid search is a complete enumeration of all possible combinations of parameters. Other proposed methods for optimizing hyperparameters are random search and Bayesian optimization.

The optimal set of hyperparameters detected by the grid search is as follows: the number of layers = 3, the dimension of the hidden state = 256, the dimension of vector mappings = 32, the length of the sequence = 128, the probability of excluding neurons = 0.3.

This model achieved a loss of cross-entropy of 0.324 during training and 0.477 at the testing stage. The learning curve graph demonstrates that the learning process converges after 30 iterations (≈28.5 minutes using a single graphics processor).

The loss graphs during training and during the testing phase can also illustrate the effect of each hyperparameter. Of particular interest to us is the probability of excluding neurons:


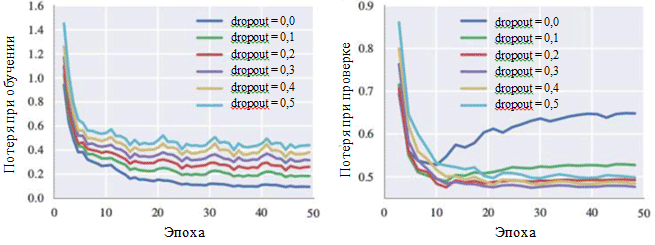
Learning curves for different exclusion method settings

In the figure, it can be seen that the elimination method really avoids over-fitting. Although if the probability of elimination is 0.0, the loss during training is minimal, at the verification stage the loss has a maximum value. Higher probability values ​​lead to an increase in losses during training and a decrease in losses during the verification phase. The minimum loss value at the verification stage when working with BachBot was recorded with an exception probability of 0.3.

Alternative assessment methods (optional)

For some models - especially for such creative applications as writing music - the loss may not be a suitable measure of the success of the system. Instead, the subjective human perception may be the best criterion.

The goal of the BachBot project is to automatically compose music that is indistinguishable from Bach's own compositions. To assess the success of the results obtained, a survey of users was conducted on the Internet. The survey was given the form of a competition in which users were asked to determine which works belong to the BachBot project, and which ones belong to the Bach project.

The survey results showed that survey participants (759 people with different levels of training) were able to accurately distinguish between two samples only in 59 percent of cases. This is only 9 percent higher than the result of random guessing! Try the BachBot survey yourself!

Adaptation of the model to harmonization

Now BachBot can calculate P (x _{t + 1} | x _t , h _t-1 ), the probability distribution for the next possible notes based on the current note and the previous hidden state. This consistent prediction model can be subsequently adapted to harmonize the melody. Such an adapted model is required to harmonize the melody modulated with the help of emotions within a musical project with the display of slides.

When working with the harmonization of the model, a predetermined tune is provided (usually this is a soprano part), and the model must then compose music for the remaining parts. To perform this task, use the best-first greedy search with the restriction that the notes of the melody are fixed. Greedy algorithms involve making decisions that are optimal from a local point of view. So, below is a simple strategy used for harmonization:

Assume that x _t are tokens in the proposed harmonization. At the time step t, if the note corresponds to the melody, then x _t is equal to the given note. Otherwise, x _t is the most likely next note in accordance with the predictions of the model. The code for such an adaptation of the model can be found on Github Feynman Liang: HarmModel.lua , harmonize.lua .

Below is an example of harmonization of the lullaby Twinkle, Twinkle, Little Star with the help of BachBot, using the above strategy.


Harmonization of the lullaby of Twinkle, Twinkle, Little Star with the help of BachBot (in the soprano part). The viola, tenor and bass parts were also filled with the BachBot

In this example, the melody of the lullaby Twinkle, Twinkle, Little Star is shown in the soprano part. After that, the viola, tenor, and bass lines were filled with the BachBot using the harmonization strategy. And here is how it sounds .

Despite the fact that BachBot has demonstrated good performance in this task, there are certain limitations associated with this model. More precisely, the algorithm does not look forward to the melody and uses only the current note of the melody and the past context to generate subsequent notes. When harmonizing a melody with people, they can cover the whole melody as a whole, which simplifies the derivation of suitable harmonizations. The fact that this model is not able to do this can lead to surprises due to limitations in the use of subsequent information that cause errors. To solve this problem, a so-called ray search can be used.

When using ray search, various lines of motion are checked. For example, instead of using only one, the most probable note that is being done at the moment, four or five of the most probable notes can be considered, after which the algorithm continues its work with each of these notes. Consideration of various options can help the model to recover from the appearance of errors . Radiation search is commonly used in natural language processing applications for creating sentences.

Melodies modulated with emotions can now be passed through this harmonization model to complete them.