The challenge with the skyscraper and the eggs - not binomial Newton?
Actually, he is the most. But first things first.
I master a python, I solve everything on Codewars. I come across a well-known task about skyscraper and eggs. The only difference is that the source data is not 100 floors and 2 eggs, but a little more.
Given: N eggs, M attempts to throw them, an endless skyscraper.
Define: the maximum floor from which you can throw an egg without breaking. Eggs are spherical in a vacuum and, if one of them has not broken, having fallen, for example, from the 99th floor, then the others will also withstand a fall from all floors less than a hundredth.
')
0 <= N, M <= 20000.
Run time of two dozen tests - 12 seconds.
We need to write the height (n, m) function, which will return the floor number for given n, m. Since it will be mentioned very often, and writing “height” every time is lazy, then everywhere, except for the code, I will designate it as f (n, m).
Let's start with zeros. Obviously, if there are no eggs or attempts to throw them, then nothing can be determined and the answer will be zero. f (0, m) = 0, f (n, 0) = 0.
Suppose there is one egg, and 10 attempts. You can risk everything and throw it right away from the hundredth floor, but if it fails, you will not be able to determine anything else, so it’s more logical to start from the first floor and go up one floor after each throw until either the attempt or the egg is over. Maximum where you can get if the egg doesn't fail - floor number 10. f (1, m) = m
Take the second egg, trying again 10. Now is it possible to risk the hundredth? It will break - there will be one more and 9 attempts, at least 9 floors will be able to pass. So maybe you need to risk not from the hundredth, but from the tenth? Is logical. Then, if successful, there will be 2 eggs and 9 attempts. By analogy, now you need to climb another 9 floors. With a series of successes - another 8, 7, 6, 5, 4, 3, 2 and 1. Total, we are on the 55th floor with two whole eggs and no attempts. The answer is the sum of the first M members of the arithmetic progression with the first member 1 and step 1. f (2, m) = (m * m + m) / 2 . It is also clear that at each step the function f (1, m) was called, as it were, but this is not yet accurate.
Continue with three eggs and ten attempts. In case of an unsuccessful first throw, the floors will be covered from below, defined by 2 eggs and 9 attempts, which means that the first throw must be made from the floor f (2, 9) + 1. Then, if successful, we have 3 eggs and 9 attempts . And for the second attempt, you need to climb f (2.8) + 1 floors. And so on, until 3 eggs and 3 attempts remain on the hands. And here is the time to be distracted by the consideration of cases with N = M, when there are as many eggs as there are attempts.
Returning to f (3, 10). In fact, at each step, everything comes down to the sum of f (2, m-1) - the number of floors that can be determined in case of failure, the units and f (3, m-1) - the number of floors that can be determined in case of success. And it becomes clear that the increase in the number of eggs and attempts is unlikely that something will change. f (n, m) = f (n - 1, m - 1) + 1 + f (n, m - 1) . And this is a universal formula that can be embodied in the code.
Of course, I had previously stepped on the rake of non-nemoisation of recursive functions and found out that f (10, 40) takes almost 40 seconds and the number of calls to itself is 97806983. But memoization also saves only at the initial intervals. If f (200,400) is executed in 0.8 seconds, then f (200, 500) in 31 seconds already. It's funny that when measuring the execution time using% timeit, the result is much less real. Obviously, the first run of the function takes most of the time, and the others simply use the results of its memoization. Lies, blatant lies and statistics.
So, for example, f (9477, 10000) appears in the tests, but my miserable f (200, 500) does not fit the right time anymore. So there is another solution, without recursion, we continue its search. I added code with counting function calls with certain parameters in order to look at what it ultimately decomposes. For 10 attempts, the following results were obtained:
f (3,10) = 7+ 1 * f (2.9) + 1 * f (2.8) + 1 * f (2.7) + 1 * f (2.6) + 1 * f (2 , 5) + 1 * f (2.4) + 1 * f (2.3) + 1 * f (3.3)
f (4,10) = 27 + 1 * f (2.8) + 2 * f (2.7) + 3 * f (2.6) + 4 * f (2.5) + 5 * f (2 , 4) + 6 * f (2,3) + 6 * f (3,3) + 1 * f (4,4)
f (5,10) = 55+ 1 * f (2.7) + 3 * f (2.6) + 6 * f (2.5) + 10 * f (2.4) + 15 * f (2 , 3) + 15 * f (3.3) + 5 * f (4.4) + 1 * f (5.5)
f (6.10) = 69+ 1 * f (2.6) + 4 * f (2.5) + 10 * f (2.4) + 20 * f (2.3) + 20 * f (3 , 3) + 10 * f (4.4) + 4 * f (5.5) + 1 * f (6.6)
f (7.10) = 55+ 1 * f (2.5) + 5 * f (2.4) + 15 * f (2.3) + 15 * f (3.3) + 10 * f (4 , 4) + 6 * f (5.5) + 3 * f (6.6) + 1 * f (7.7)
f (8,10) = 27 + 1 * f (2.4) + 6 * f (2.3) + 6 * f (3.3) + 5 * f (4.4) + 4 * f (5 , 5) + 3 * f (6.6) + 2 * f (7.7) + 1 * f (8.8)
f (9,10) = 7+ 1 * f (2.3) + 1 * f (3.3) + 1 * f (4.4) + 1 * f (5.5) + 1 * f (6 , 6) + 1 * f (7.7) + 1 * f (8.8) + 1 * f (9.9)
Some regularity can be seen:

These coefficients are theoretically calculated. Each blue is the sum of the top and left. And purple - the same blue, only in reverse order. You can calculate, but this is recursion again, and I was disappointed in it. Most likely, many (it is a pity that I am not) have already learned these numbers, but for the time being I will keep the intrigue by following my own solution path. I decided to spit on them and go to the other side.
He opened the Excel, built a sign with the results of the function and began to look out for patterns. C3 = IF (C $ 2> $ B3; 2 ^ $ B3-1; C2 + B2 + 1), where $ 2 is a row with the number of eggs (1-13), $ B is a column with the number of attempts (1-20), C3 is a cell at the intersection of two eggs and one attempt.
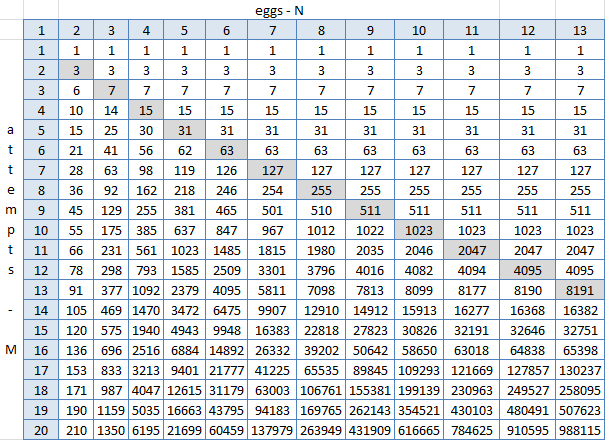
The gray diagonal is N = M and here it is clearly seen that nothing changes to the right of it (for N> M). It can be seen that it cannot be otherwise, because these are all the results of the formula in which it is given that each cell is equal to the sum of the top, top left, and one. But some universal formula, where you can substitute N and M and get the number of the floor, could not be found. Spoiler: it does not exist. But on the other hand, just creating this table in Excel looks like, maybe you can generate the same python and drag answers from it?
I remember that there is NumPy, which is just designed to work with multidimensional arrays, why not try it? To begin, we need a one-dimensional array of zeros N + 1 in size. And a one-dimensional array of units of size N. We take the first array from the zero to the penultimate element, add element by element with the first array from the first element to the last and with an array of units. We add a zero to the resulting array at the beginning. Repeat M times. Element number N of the resulting array will be the answer. The first 3 steps look like this:
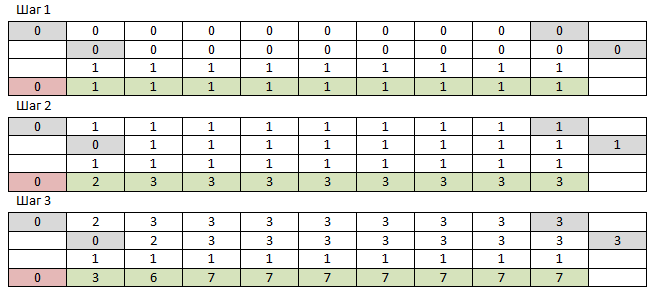
NumPy works so fast that I didn’t save the whole table - every time I read the necessary line again. But one thing - the result of work on large numbers was wrong. Older categories like those, and younger - no. This is how the errors of arithmetic of floating-point numbers accumulated from the multiple addition look like. It does not matter - you can also change the type of the array to int. No, trouble - it turned out that for speed, NumPy works only with its data types, and its int, unlike Python int, can be no more than 2 ^ 64-1, after which it overflows silently and continues from -2 ^ 64. And I actually expect the numbers under three thousand characters. But it works very fast, f (9477, 10000) is performed for 233 ms, just some kind of nonsense is obtained at the output. I will not even give the code, since this is the case. I'll try to do the same thing with a clean python.
44 seconds to calculate f (9477, 10000), a bit too much. But absolutely for sure. What can be optimized? The first is that there is no need to count everything that is to the right of the diagonal M, M. The second is to count the last array as a whole, for the sake of a single cell. For this, the last two cells of the previous one will fit. To calculate f (10, 20), only these gray cells will suffice:
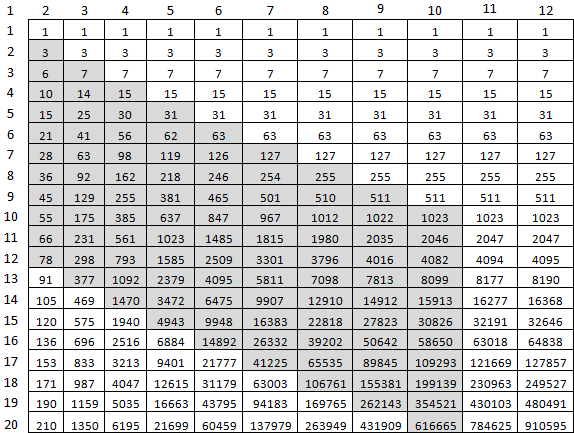
And so it looks like in code:
And what do you think? f (9477, 10000) in 2 seconds! But these inputs are too good, the length of the array at any stage will be no more than 533 elements (10000-9477). Check on f (5477, 10000) - 11 seconds. Too good, but only compared to 44 seconds - twenty tests with such time will not pass.
It's not that. But once there is a problem, then there is a solution, the search continues. I again began to look at the Excel table. The cell to the left of (m, m) is always one less. And the cell to the left of it is already gone, the difference in each row becomes larger. The cell below (m, m) is always twice as large. And the cell below it is no longer double, but a little less, but for each column it is different, the farther, the more. And the numbers on one line first grow fast, and slowly after the middle. Let me build a table of differences between neighboring cells, maybe there will be some pattern?
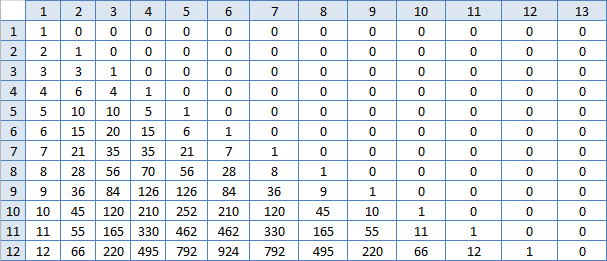
Bah, familiar numbers! That is, the sum of these N numbers in row number M is the answer? True, counting them is about the same thing as I have already done; this is unlikely to speed up the work greatly. But we must try:
Not to say that a more optimal solution. On some data it works faster, on some slower. Must go deeper. What is this triangle with numbers that appeared in the solution twice? I am ashamed to admit, but the highest mathematics, where the triangle probably figured, I safely forgot, so I had to google.
Pascal's triangle , so it is officially called. An infinite table of binomial coefficients. So the answer to the problem with N eggs and M throws is the sum of the first N coefficients in the expansion of the Newton binomial of the Mth degree, except for the zero one.
An arbitrary binomial coefficient can be calculated through the factorials of the line number and the number of the coefficient in the line: bk = m! / (N! * (Mn!)). But the most pleasant thing is that you can successively calculate the numbers in a line, knowing its number and the zero coefficient (always one): bk [n] = bk [n-1] * (m - n + 1) / n. At each step, the numerator is reduced by one, and the denominator increases. And the concise final solution looks like this:
33 ms on the calculation of f (9477, 10000)! This solution can also be optimized, although in the specified ranges and it works fine. If n lies in the second half of the triangle, then you can invert it into mn, count the sum of the first n coefficients and take it away from 2 ^ m-2. If n is close to the middle and m is odd, then calculations can also be reduced: the sum of the first half of the line will be 2 ^ (m-1) -1, the last coefficient in the first half can be calculated through factorials, its number is (m-1) / 2, and then either continue to add the coefficients, if n is in the right half of the triangle, or subtract, if in the left. If m is even, then half of the line is no longer calculated, but you can find the sum of the first m / 2 + 1 coefficients by calculating the average factorial and adding half of it to 2 ^ (m-1) -1. On the input data in the region of 10 ^ 6, this significantly reduces the execution time.
Already after a successful decision, I began to look for someone else's research on this issue, but found only the very thing from interviews, with only two eggs, and this is not sporting. The Internet will be incomplete without my decision, I decided, and here it is.
Formulation of the problem
I master a python, I solve everything on Codewars. I come across a well-known task about skyscraper and eggs. The only difference is that the source data is not 100 floors and 2 eggs, but a little more.
Given: N eggs, M attempts to throw them, an endless skyscraper.
Define: the maximum floor from which you can throw an egg without breaking. Eggs are spherical in a vacuum and, if one of them has not broken, having fallen, for example, from the 99th floor, then the others will also withstand a fall from all floors less than a hundredth.
')
0 <= N, M <= 20000.
Run time of two dozen tests - 12 seconds.
Finding a solution
We need to write the height (n, m) function, which will return the floor number for given n, m. Since it will be mentioned very often, and writing “height” every time is lazy, then everywhere, except for the code, I will designate it as f (n, m).
Let's start with zeros. Obviously, if there are no eggs or attempts to throw them, then nothing can be determined and the answer will be zero. f (0, m) = 0, f (n, 0) = 0.
Suppose there is one egg, and 10 attempts. You can risk everything and throw it right away from the hundredth floor, but if it fails, you will not be able to determine anything else, so it’s more logical to start from the first floor and go up one floor after each throw until either the attempt or the egg is over. Maximum where you can get if the egg doesn't fail - floor number 10. f (1, m) = m
Take the second egg, trying again 10. Now is it possible to risk the hundredth? It will break - there will be one more and 9 attempts, at least 9 floors will be able to pass. So maybe you need to risk not from the hundredth, but from the tenth? Is logical. Then, if successful, there will be 2 eggs and 9 attempts. By analogy, now you need to climb another 9 floors. With a series of successes - another 8, 7, 6, 5, 4, 3, 2 and 1. Total, we are on the 55th floor with two whole eggs and no attempts. The answer is the sum of the first M members of the arithmetic progression with the first member 1 and step 1. f (2, m) = (m * m + m) / 2 . It is also clear that at each step the function f (1, m) was called, as it were, but this is not yet accurate.
Continue with three eggs and ten attempts. In case of an unsuccessful first throw, the floors will be covered from below, defined by 2 eggs and 9 attempts, which means that the first throw must be made from the floor f (2, 9) + 1. Then, if successful, we have 3 eggs and 9 attempts . And for the second attempt, you need to climb f (2.8) + 1 floors. And so on, until 3 eggs and 3 attempts remain on the hands. And here is the time to be distracted by the consideration of cases with N = M, when there are as many eggs as there are attempts.
And at the same time and those when more eggs.
But here everything is obvious - we will not need eggs over and above those that are broken, even if each throw is unsuccessful. f (n, m) = f (m, m) if n> m . And that's all equally, 3 eggs, 3 throws. If the first egg is broken, then you can check f (2, 2) floors to the bottom, and if not broken, then f (3,2) floors to the top, that is, the same f (2, 2). Total f (3, 3) = 2 * f (2, 2) + 1 = 7. And f (4, 4), by analogy, consists of two f (3, 3) and one, and will be equal to 15. Everything this is reminiscent of a power of two, and let’s write: f (m, m) = 2 ^ m - 1 .
It looks like a binary search in the physical world: we start from the floor number 2 ^ (m-1), if we succeed, we go up 2 ^ (m-2) floors up, and if we fail, we go down as many down, and so until the attempts are over. In our case, all the time we go up.
It looks like a binary search in the physical world: we start from the floor number 2 ^ (m-1), if we succeed, we go up 2 ^ (m-2) floors up, and if we fail, we go down as many down, and so until the attempts are over. In our case, all the time we go up.
Returning to f (3, 10). In fact, at each step, everything comes down to the sum of f (2, m-1) - the number of floors that can be determined in case of failure, the units and f (3, m-1) - the number of floors that can be determined in case of success. And it becomes clear that the increase in the number of eggs and attempts is unlikely that something will change. f (n, m) = f (n - 1, m - 1) + 1 + f (n, m - 1) . And this is a universal formula that can be embodied in the code.
from functools import lru_cache @lru_cache() def height(n,m): if n==0 or m==0: return 0 elif n==1: return m elif n==2: return (m**2+m)/2 elif n>=m: return 2**n-1 else: return height(n-1,m-1)+1+height(n,m-1) Of course, I had previously stepped on the rake of non-nemoisation of recursive functions and found out that f (10, 40) takes almost 40 seconds and the number of calls to itself is 97806983. But memoization also saves only at the initial intervals. If f (200,400) is executed in 0.8 seconds, then f (200, 500) in 31 seconds already. It's funny that when measuring the execution time using% timeit, the result is much less real. Obviously, the first run of the function takes most of the time, and the others simply use the results of its memoization. Lies, blatant lies and statistics.
Recursion is not needed, looking further
So, for example, f (9477, 10000) appears in the tests, but my miserable f (200, 500) does not fit the right time anymore. So there is another solution, without recursion, we continue its search. I added code with counting function calls with certain parameters in order to look at what it ultimately decomposes. For 10 attempts, the following results were obtained:
f (3,10) = 7+ 1 * f (2.9) + 1 * f (2.8) + 1 * f (2.7) + 1 * f (2.6) + 1 * f (2 , 5) + 1 * f (2.4) + 1 * f (2.3) + 1 * f (3.3)
f (4,10) = 27 + 1 * f (2.8) + 2 * f (2.7) + 3 * f (2.6) + 4 * f (2.5) + 5 * f (2 , 4) + 6 * f (2,3) + 6 * f (3,3) + 1 * f (4,4)
f (5,10) = 55+ 1 * f (2.7) + 3 * f (2.6) + 6 * f (2.5) + 10 * f (2.4) + 15 * f (2 , 3) + 15 * f (3.3) + 5 * f (4.4) + 1 * f (5.5)
f (6.10) = 69+ 1 * f (2.6) + 4 * f (2.5) + 10 * f (2.4) + 20 * f (2.3) + 20 * f (3 , 3) + 10 * f (4.4) + 4 * f (5.5) + 1 * f (6.6)
f (7.10) = 55+ 1 * f (2.5) + 5 * f (2.4) + 15 * f (2.3) + 15 * f (3.3) + 10 * f (4 , 4) + 6 * f (5.5) + 3 * f (6.6) + 1 * f (7.7)
f (8,10) = 27 + 1 * f (2.4) + 6 * f (2.3) + 6 * f (3.3) + 5 * f (4.4) + 4 * f (5 , 5) + 3 * f (6.6) + 2 * f (7.7) + 1 * f (8.8)
f (9,10) = 7+ 1 * f (2.3) + 1 * f (3.3) + 1 * f (4.4) + 1 * f (5.5) + 1 * f (6 , 6) + 1 * f (7.7) + 1 * f (8.8) + 1 * f (9.9)
Some regularity can be seen:

These coefficients are theoretically calculated. Each blue is the sum of the top and left. And purple - the same blue, only in reverse order. You can calculate, but this is recursion again, and I was disappointed in it. Most likely, many (it is a pity that I am not) have already learned these numbers, but for the time being I will keep the intrigue by following my own solution path. I decided to spit on them and go to the other side.
He opened the Excel, built a sign with the results of the function and began to look out for patterns. C3 = IF (C $ 2> $ B3; 2 ^ $ B3-1; C2 + B2 + 1), where $ 2 is a row with the number of eggs (1-13), $ B is a column with the number of attempts (1-20), C3 is a cell at the intersection of two eggs and one attempt.

The gray diagonal is N = M and here it is clearly seen that nothing changes to the right of it (for N> M). It can be seen that it cannot be otherwise, because these are all the results of the formula in which it is given that each cell is equal to the sum of the top, top left, and one. But some universal formula, where you can substitute N and M and get the number of the floor, could not be found. Spoiler: it does not exist. But on the other hand, just creating this table in Excel looks like, maybe you can generate the same python and drag answers from it?
NumPy, you do not
I remember that there is NumPy, which is just designed to work with multidimensional arrays, why not try it? To begin, we need a one-dimensional array of zeros N + 1 in size. And a one-dimensional array of units of size N. We take the first array from the zero to the penultimate element, add element by element with the first array from the first element to the last and with an array of units. We add a zero to the resulting array at the beginning. Repeat M times. Element number N of the resulting array will be the answer. The first 3 steps look like this:

NumPy works so fast that I didn’t save the whole table - every time I read the necessary line again. But one thing - the result of work on large numbers was wrong. Older categories like those, and younger - no. This is how the errors of arithmetic of floating-point numbers accumulated from the multiple addition look like. It does not matter - you can also change the type of the array to int. No, trouble - it turned out that for speed, NumPy works only with its data types, and its int, unlike Python int, can be no more than 2 ^ 64-1, after which it overflows silently and continues from -2 ^ 64. And I actually expect the numbers under three thousand characters. But it works very fast, f (9477, 10000) is performed for 233 ms, just some kind of nonsense is obtained at the output. I will not even give the code, since this is the case. I'll try to do the same thing with a clean python.
Iterated, iterated, but not vyiteriroval
def height(n, m): arr = [0]*(n+1) while m > 0: arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) m-=1 return arr[n] 44 seconds to calculate f (9477, 10000), a bit too much. But absolutely for sure. What can be optimized? The first is that there is no need to count everything that is to the right of the diagonal M, M. The second is to count the last array as a whole, for the sake of a single cell. For this, the last two cells of the previous one will fit. To calculate f (10, 20), only these gray cells will suffice:

And so it looks like in code:
def height(n, m): arr = [0, 1, 1] i = 1 while i < n and i < mn: # m,m arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) arr += [arr[-1]] i+=1 arr.pop(-1) while i < n or i < mn: # arr = list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) arr = arr + [arr[-1]+1] if n > len(arr) else [0] + arr i+=1 while i < m: # , - arr = list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) i+=1 return arr[0] And what do you think? f (9477, 10000) in 2 seconds! But these inputs are too good, the length of the array at any stage will be no more than 533 elements (10000-9477). Check on f (5477, 10000) - 11 seconds. Too good, but only compared to 44 seconds - twenty tests with such time will not pass.
It's not that. But once there is a problem, then there is a solution, the search continues. I again began to look at the Excel table. The cell to the left of (m, m) is always one less. And the cell to the left of it is already gone, the difference in each row becomes larger. The cell below (m, m) is always twice as large. And the cell below it is no longer double, but a little less, but for each column it is different, the farther, the more. And the numbers on one line first grow fast, and slowly after the middle. Let me build a table of differences between neighboring cells, maybe there will be some pattern?
Warmer

Bah, familiar numbers! That is, the sum of these N numbers in row number M is the answer? True, counting them is about the same thing as I have already done; this is unlikely to speed up the work greatly. But we must try:
f (9477, 10000): 17 seconds
def height(n, m): arr = [1,1] while m > 1: arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) + [1] m-=1 return sum(arr[1:n+1]) Or 8, if you count only half of the triangle
def height(n, m): arr = [1,1] while m > 2 and len(arr) < n+2: # , n < arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) arr += [arr[-1]] m-=2 while m > 1: arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) m-=1 if len(arr) < n+1: arr += arr[::-1][1:] # n , return sum(arr[1:n+1]) Not to say that a more optimal solution. On some data it works faster, on some slower. Must go deeper. What is this triangle with numbers that appeared in the solution twice? I am ashamed to admit, but the highest mathematics, where the triangle probably figured, I safely forgot, so I had to google.
Bingo!
Pascal's triangle , so it is officially called. An infinite table of binomial coefficients. So the answer to the problem with N eggs and M throws is the sum of the first N coefficients in the expansion of the Newton binomial of the Mth degree, except for the zero one.
An arbitrary binomial coefficient can be calculated through the factorials of the line number and the number of the coefficient in the line: bk = m! / (N! * (Mn!)). But the most pleasant thing is that you can successively calculate the numbers in a line, knowing its number and the zero coefficient (always one): bk [n] = bk [n-1] * (m - n + 1) / n. At each step, the numerator is reduced by one, and the denominator increases. And the concise final solution looks like this:
def height(n, m): h, bk = 0, 1 # for i in range(1, n + 1): bk = bk * m // ih += bk m-=1 return h 33 ms on the calculation of f (9477, 10000)! This solution can also be optimized, although in the specified ranges and it works fine. If n lies in the second half of the triangle, then you can invert it into mn, count the sum of the first n coefficients and take it away from 2 ^ m-2. If n is close to the middle and m is odd, then calculations can also be reduced: the sum of the first half of the line will be 2 ^ (m-1) -1, the last coefficient in the first half can be calculated through factorials, its number is (m-1) / 2, and then either continue to add the coefficients, if n is in the right half of the triangle, or subtract, if in the left. If m is even, then half of the line is no longer calculated, but you can find the sum of the first m / 2 + 1 coefficients by calculating the average factorial and adding half of it to 2 ^ (m-1) -1. On the input data in the region of 10 ^ 6, this significantly reduces the execution time.
Already after a successful decision, I began to look for someone else's research on this issue, but found only the very thing from interviews, with only two eggs, and this is not sporting. The Internet will be incomplete without my decision, I decided, and here it is.
Source: https://habr.com/ru/post/423679/
All Articles