Disk caching of lazy computing trees
The concept of lazy computing is hardly worth talking about in detail. The idea to do the same thing less often, especially if it is long and heavy, is as old as the world. Because immediately to the point.
According to the understanding of the author of this text, a normal lenifier should:
- Save calculations between program calls.
- Track changes to the calculation tree.
- Have a moderately transparent syntax.

Concept
In order:
- Save calculations between program calls:
Indeed, if we call the same script several tens or hundreds of times a day, why recalculate the same thing every time the script is called, if you can store the result object in a file. It is better to pull up the object from the disk, but ... we must be sure of its relevance. Suddenly the script is rewritten and the saved object is outdated. Based on this, we can not just take and in fact the presence of the file to load the object. Hence the second point. - Track changes in the calculation tree:
The need to update an object should be calculated based on the data on the arguments of the function generating it. So we will be sure that the loaded object is valid. Indeed, for a pure function, the return value depends only on the arguments. So, while we cache the results of pure functions and monitor the change of arguments, we can be sure that the cache is relevant. At the same time, if a calculated object depends on another cached (lazy) object, which in turn depends on another, you need to correctly work out changes in these objects, timely updating the chained nodes that have ceased to be relevant. On the other hand, it would be nice to consider that we do not always need to load the data of the entire chain of calculations. Often enough to download only the final result object. - Have a moderately transparent syntax:
This item is clear. If in order to rewrite the script for lazy calculations it is necessary to change all the code, this is so-so decision. Changes should be made to a minimum.
This chain of reasoning led to a technical solution, designed in the python library evalcache (links at the end of the article).
Syntactic solution and mechanism of work
import evalcache import hashlib import shelve lazy = evalcache.Lazy(cache = shelve.open(".cache"), algo = hashlib.sha256) @lazy def summ(a,b,c): return a + b + c @lazy def sqr(a): return a * a a = 1 b = sqr(2) c = lazy(3) lazyresult = summ(a, b, c) result = lazyresult.unlazy() print(lazyresult) #f8a871cd8c85850f6bf2ec96b223de2d302dd7f38c749867c2851deb0b24315c print(result) #8 How it works?
The first thing that catches your eye here is the creation of a lazy decorator. This syntactic solution is fairly standard for Python-based lenificators. A lazy decorator is passed a cache object in which the lenifier will store the results of the calculations. The dict-like interface requirements are imposed on the cache type. In other words, we are able to cache into everything that implements the same interface that the type dict has. For the demonstration in the example above, a dictionary from the shelve library is used.
Also, the decorator is transferred to the hash protocol, which he will use to build the hash keys of objects and some additional options (write permission, read permission, debug output), which can be found in the documentation or code.
The decorator can be applied both to functions and to objects of other types. At this moment, a lazy object with a hash key calculated on the basis of the representation (or with the help of a specially defined hash function) is built on their basis.
A key feature of the library is that a lazy object can spawn other lazy objects, with the hash key of the parent (or parents) mixed into the hash key of the child. For lazy objects, it is allowed to use an attribute operation, use calls ( __call__ ) of objects, use operators.
When passing through the script, in fact, no calculations are made. For b, the square is not calculated, and for lazyresult the sum of the arguments is not considered. Instead, a tree of operations is constructed and the hash keys of lazy objects are calculated.
Real calculations (if the result was not previously put in the cache) will be performed only in the line: result = lazyresult.unlazy()
If the object was calculated earlier, it will be loaded from the file.
You can visualize the construction tree:
evalcache.print_tree(lazyresult) ... generic: <function summ at 0x7f1cfc0d5048> args: 1 generic: <function sqr at 0x7f1cf9af29d8> args: 2 ------- 3 ------- Since object hashes are built on the basis of the data about the arguments that generate these objects, when the argument changes, the object hash changes and along with it the hashes of the entire chain dependent on it change in a cascade. This allows you to keep cache data up to date, making updates on time.
Lazy objects line up in a tree. If we perform an unlazy operation on one of the objects, exactly as many objects as necessary to obtain a valid result will be loaded and recalculated. Ideally, the required object will simply be loaded. In this case, the algorithm will not pull up forming objects into memory.
In action
Above was a simple example that shows syntax, but does not demonstrate the computational power of the approach.
Here is an example a little more approximate to real life (sympy is used).
#!/usr/bin/python3.5 from sympy import * import numpy as np import math import evalcache lazy = evalcache.Lazy(evalcache.DirCache(".evalcache"), diag = True) pj1, psi, y0, gamma, gr= symbols("pj1 psi y0 gamma gr") ###################### Construct sympy expression ##################### F = 2500 xright = 625 re = 625 y0 = 1650 gr = 2*math.pi / 360 #gamma = pi / 2 xj1q = xright + re * (1 - cos(psi)) yj1q = (xright + re) * tan(psi) - re * sin(psi) #+ y0 pj1 = sqrt(xj1q**2 + yj1q**2) pj2 = pj1 + y0 * sin(psi) zj2 = (pj2**2)/4/F asqrt = sqrt(pj2**2 + 4*F**2) xp2 = 2*F / asqrt yp2 = pj2 / asqrt xp3 = yp2 yp3 = -xp2 xmpsi = 1295 gmpsi = 106 * gr aepsi = 600 bepsi = 125 b = 0.5*(1-cos(pi * gamma / gmpsi)) p1 = ( (gamma * xmpsi / gmpsi * xp2) * (1-b) + (aepsi * xp2 * sin(gamma) + bepsi * yp2 * (1-cos(gamma)))*b + pj1 ) ####################################################################### #First lazy node. Simplify is long operation. #Sympy has very good representations for expressions print("Expression:", repr(p1)) print() p1 = lazy(simplify)(p1) ######################################################################################### ## Really don't need to lazify fast operations Na = 200 angles = [t * 2 * math.pi / 360 / Na * 106 for t in range(0,Na+1)] N = int(200) a = (np.arange(0,N+1) - N/2) * 90/360*2*math.pi/N ######################################################################################### @lazy def genarray(angles, a, p1): points = [] for i in range(0, len(angles)): ex = p1.subs(gamma, angles[i]) func = lambdify(psi, ex, 'numpy') # returns a numpy-ready function rads = func(a) xs = rads*np.cos(a) ys = rads*np.sin(a) arr = np.column_stack((xs,ys,[i*2]*len(xs))) points.append(arr) return points #Second lazy node. arr = genarray(angles, a, p1).unlazy() print("\nResult list:", arr.__class__, len(arr)) Operations to simplify symbolic expressions are extremely costly and literally ask for lenification. Further construction of a large array is performed even longer, but thanks to lazification, the results will be pulled from the cache. Note that if at the top of the script where the sympy expression is generated, some factors are changed, the results will be recalculated because the hash key of the lazy object changes (thanks to the cool __repr__ operators).
Quite often there is a situation when the researcher conducts computational experiments on a long time generated object. It can use several scripts to separate the generation and use of the object, which can cause problems with late data update. The proposed approach can facilitate this case.
What was it all for
evalcache is part of the zencad project. This is a small scripted Kadik, inspired and exploiting the same ideas as openscad. Unlike mesh-oriented openscad, in zencad, running on the opencascade core, the object representation is brep, and the scripts are written in python.
Geometric operations are often performed long. The lack of scripted cad systems is that every time the script is launched, the product is completely recalculated again. Moreover, with the growth and complication of the model, the overheads grow by no means linear. This leads to the fact that you can work comfortably only with extremely small models.
The evalcache task was to smooth the problem. In zencad, all operations are declared as lazy.
Examples:
#!/usr/bin/python3 #coding: utf-8 from zencad import * xgate = 14.65 ygate = 11.6 zgate = 11 t = (xgate - 11.7) / 2 ear_r = 8.6/2 ear_w = 7.8 - ear_r ear_z = 3 hx_h = 2.0 bx = xgate + ear_w by = 2 bz = ear_z+1 gate = ( box(xgate, ygate, t).up(zgate - t) + box(t, ygate, zgate) + box(t, ygate, zgate).right(xgate - t) ) gate = gate.fillet(1, [5, 23,29, 76]) gate = gate.left(xgate/2) ear = (box(ear_w, ear_r * 2, ear_z) + cylinder(r = ear_r, h = ear_z).forw(ear_r).right(ear_w)).right(xgate/2 - t) hx = linear_extrude( ngon(r = 2.5, n = 6).rotateZ(deg(90)).forw(ear_r), hx_h ).up(ear_z - hx_h).right(xgate/2 -t + ear_w) m = ( gate + ear + ear.mirrorYZ() - hx - hx.mirrorYZ() - box(xgate-2*t, ygate, zgate, center = True).forw(ygate/2) - box(bx, by, bz, center = True).forw(ear_r).up(bz/2) - cylinder(r = 2/2, h = 100, center = True).right(xgate/2-t+ear_w).forw(ear_r) - cylinder(r = 2/2, h = 100, center = True).left(xgate/2-t+ear_w).forw(ear_r) ) display(m) show() This script generates the following model: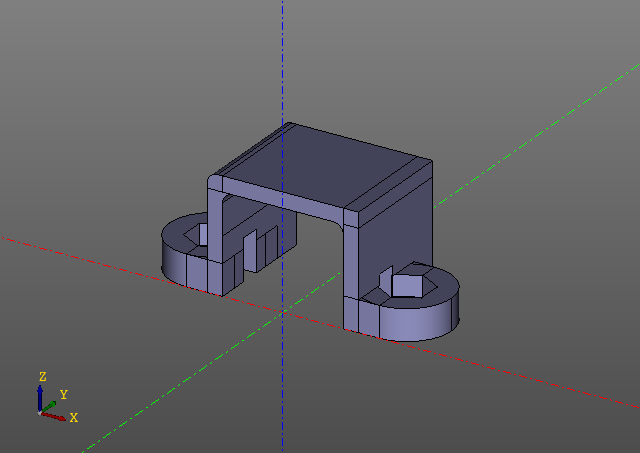
Please note that there are no evalcache calls in the script. The trick is that lenification is embedded in the zencad library itself and at first glance it’s not even visible from the outside, although all the work here is working with lazy objects, and the direct calculation is performed only in the 'display' function. Of course, if some model parameter is changed, the model will be recalculated from the place where the first hash key has changed.
Here is another example. This time we will limit ourselves to pictures: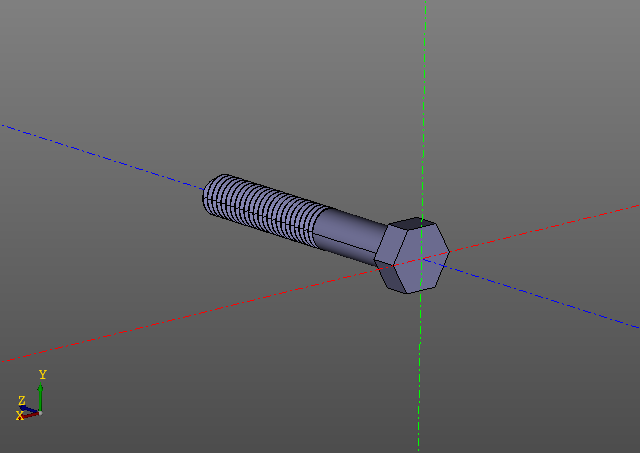
Scaling a threaded surface is no easy task. On my computer, such a bolt is built in about ten seconds ... It is more pleasant to edit a model with the threads of a lot using caching.
And now it's a miracle:
The intersection of threaded surfaces is a difficult design problem. Practical value, but no, except for checking mathematics. The calculation takes a minute and a half. A worthy goal for lazification.
Problems
The cache may not work as intended.
Cache errors can be divided into false positive and false negative .
False negative errors
False negative errors are situations when the result of the calculation is in the cache, but the system has not found it.
This happens if the hash key algorithm used by evalcache for some reason produced a different key for re-evaluation. If a hash function is not redefined for a cached type object, evalcache uses the __repr__ object to build the key.
An error happens, for example, if the class being leased does not override the standard object.__repr__ , which changes from start to start. Or, if redefined __repr__ , it somehow depends on changing data that is insignificant for calculating (like an object address or a time stamp).
Poorly:
class A: def __init__(self): self.i = 3 A_lazy = lazy(A) A_lazy().unlazy() # - __repr__. Good:
class A: def __init__(self): self.i = 3 def __repr__(self): return "A({})".format(self.i) A_lazy = lazy(A) A_lazy().unlazy() # . False negative errors lead to the fact that lenification does not work. The object will be recalculated with each new execution of the script.
False positive errors
This is a more vile type of error, since it leads to errors in the final object of the calculation:
It can happen for two reasons.
- Incredible:
There was a hash key collision in the cache. For the sha256 algorithm, which has a space of 115 1152020232316195423570985008687907853269984665640564039457584007913129639936 possible keys, the probability of a collision is negligible. - Likely:
The representation of the object (or the overridden hash function) does not fully describe it, or it is the same as the representation of an object of another type.
class A: def __init__(self): self.i = 3 def __repr__(self): return "({})".format(self.i) class B: def __init__(self): self.i = 3 def __repr__(self): return "({})".format(self.i) A_lazy = lazy(A) B_lazy = lazy(B) a = A_lazy().unlazy() b = B_lazy().unlazy() #. B, A. Both problems are related to the incompatible __repr__ object. If for some reason you cannot rewrite the type of the __repr__ method, the library allows you to specify a special hash function for the user type.
About analogues
There are many libraries of lenification, which basically consider it sufficient to perform the calculation no more than once per script call.
There are many disk caching libraries that, at your request, will save an object with the necessary key for you.
But I still could not find the libraries that would allow caching the results on the execution tree. If they are, please, opt.
References:
')
Source: https://habr.com/ru/post/422937/
All Articles