What is the idea of ​​sorting choices?

1. In the unsorted subarray, a local maximum (minimum) is searched.
2. The found maximum (minimum) is interchanged with the last (first) element in the subarray.
3. If unsorted subarrays are left in the array, see item 1.

A small lyrical digression. Initially, in my series of articles, I planned to consistently present the material on sorting classes in a strict queue. After the library sorting , articles about other interpolating algorithms were planned: solitaire sorting, sorting by the Young table, sorting by inversion, etc.

')

However, now non-linearity is in a trend, therefore, not having written all the publications about sorting inserts yet, today I will begin a parallel branch about sorting by choice. Then I will do the same for other algorithmic classes: merge sorts, distribution sorts, etc. In general, this will allow writing publications on one topic or another. With such a thematic alternation will be more fun.

Sort by selection :: Selection sort

Simple and simple - we pass through the array in search of the maximum element. The maximum found is swapped with the last element. The unassorted part of the array has decreased by one element (it does not include the last element, where we have moved the found maximum). We apply the same actions to this unsorted part - we find the maximum and put it at the last place in the unsorted part of the array. And so on until the unsorted part of the array is reduced to one element.

def selection(data): for i, e in enumerate(data): mn = min(range(i, len(data)), key=data.__getitem__) data[i], data[mn] = data[mn], e return data 

Sorting a simple choice is a coarse double search. Can it be improved? We analyze several modifications.

Double Sort Selection :: Double selection sort

A similar idea is used in shaker sorting , which is a variant of bubble sorting. Passing along the unsorted part of the array, in addition to the maximum, we also find a minimum along the way. We put a minimum on the first place, a maximum on the last. Thus, the unsorted part at each iteration is reduced by two elements at once.



At first glance, it seems that this speeds up the algorithm by 2 times - after each pass the unsorted subarray is reduced not from one, but from two sides at once. But at the same time the number of comparisons increased by 2 times, and the number of swaps remained unchanged. Double selection only slightly increases the speed of the algorithm, and in some languages ​​it even works for some reason more slowly.

The difference between sorting and sorting inserts

It may seem that sorting by selection and sorting by inserts is the essence of the same thing, a general class of algorithms. Well, or sorting inserts - sort of sorting choice. Or sorting by choice - a special case of sorting inserts. Both there and there, we take turns from the unsorted part of the array to extract the elements and redirect them to the sorted area.



The main difference: in sorting inserts, we extract any element from the unsorted part of the array and insert it in its place in the sorted part. In sorting by choice, we purposefully look for the maximum element (or minimum) with which we supplement the sorted part of the array. In the inserts we are looking for where to insert the next element, and in the selection we already know in advance where we will put it, but it is required to find the element corresponding to this place.



This makes both classes of algorithms completely different from each other in their nature and applied methods.

Bingo sorting :: Bingo sort

An interesting feature of the sorting choice is the independence of the speed of the nature of the data being sorted.



For example, if an array is almost sorted, then, as you know, sorting by inserts will process it much faster (even faster than quick sorting). A reverse-ordered array for sorting inserts is a degenerate case, it will sort it as long as possible.



And for sorting by choice, the partial or reverse ordering of an array does not matter - it will process it at about the same speed as the usual random. Also, for classical sorting by choice, it does not matter whether the array consists of unique or duplicate elements - this has practically no effect on speed.



But in principle, you can contrive and modify the algorithm so that with some data sets it works faster. For example, bingo sorting takes into account if the array consists of duplicate elements.







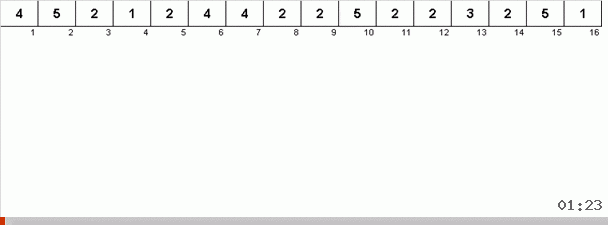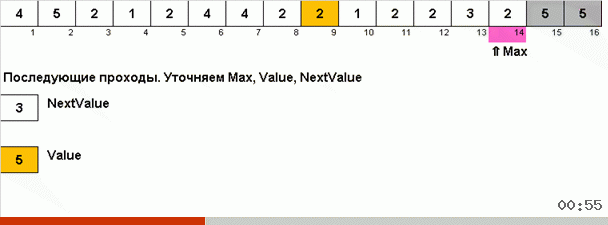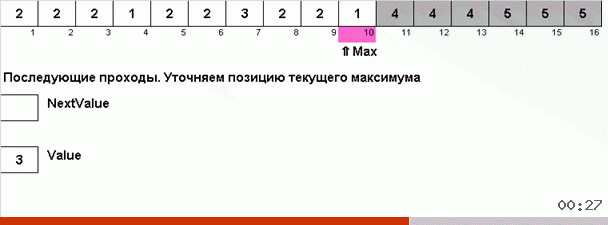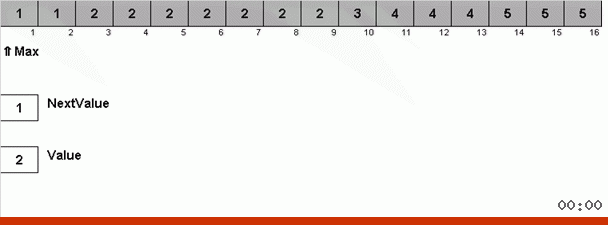
Here the trick is that in the unordered part not only the maximum element is remembered, but the maximum is determined for the next iteration. This allows for repeated maxima not to look for them again each time, but to put in their place as soon as this maximum was met once again in the array.



Algorithmic complexity remained the same. But if the array consists of repeating numbers, then bingo-sorting will cope ten times faster than regular sorting by choice.

 # - def bingo(data): #  . max = len(data) - 1 nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 #  . while max: value = nextValue nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] == value: data[i], data[max] = data[max], data[i] max -= 1 elif data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 return data 

Cyclic sort :: Cycle sort

Cyclic sorting is interesting (and valuable from a practical point of view) in that changes among the elements of an array occur if and only if the element is put in its final place. This can be useful if rewriting in an array is too expensive and in order to take care of physical memory, it is necessary to minimize the number of changes to the elements of the array.







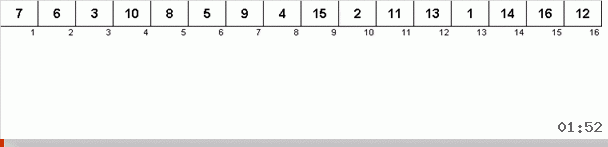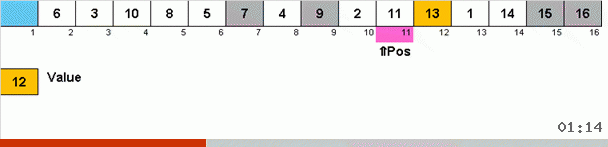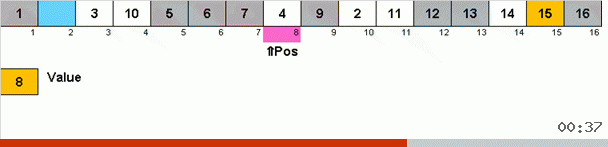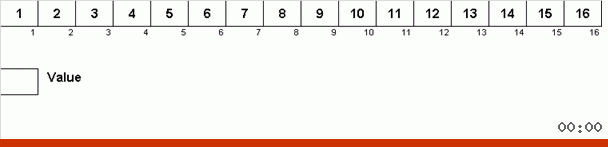
It works like this. We iterate over the array, call X the next cell in this outer loop. And look at what place in the array you need to insert the next element from this cell. At the place where you want to paste is some other element, we send it to the clipboard. For this element in the buffer, we also look for its place in the array (and insert it to this place, and send an element to the buffer that is in this place). And for the new number in the buffer, we perform the same actions. How long should this process continue? Until the next element in the clipboard is the element that needs to be inserted in cell X (the current place in the array in the main loop of the algorithm). Sooner or later, this moment will occur and then in the external cycle you can go to the next cell and repeat the same procedure for it.



In other sorts of choices, we look for the maximum / minimum to put them in the last / first place. In cycle sort, it turns out that the minimum in the first place in the subarray is, as it were, itself, in the process of how several other elements are put in their rightful places somewhere in the middle of the array.



And here the algorithmic complexity also remains within O ( n ² ). In practice, cyclic sorting works even several times slower than normal sorting by choice, since you have to run around the array more and compare more often. This is the price for the minimum possible number of overwrites.

 #   def cycle(data): #        for cycleStart in range(0, len(data) - 1): value = data[cycleStart] # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      ,   #      if pos == cycleStart: continue #   ,     #        while value == data[pos]: pos += 1 data[pos], value = value, data[pos] #      , #         while pos != cycleStart: # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      #      while value == data[pos]: pos += 1 data[pos], value = value, data[pos] return data 

Pancake sorting

The algorithm, which mastered all levels of life - from bacteria to Bill Gates .







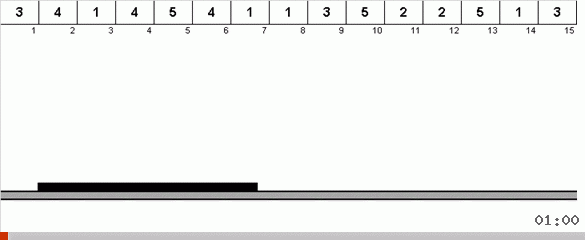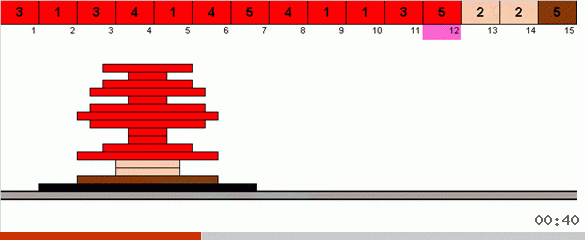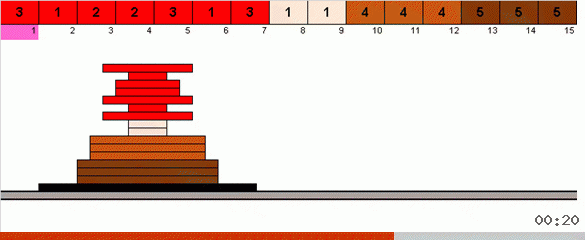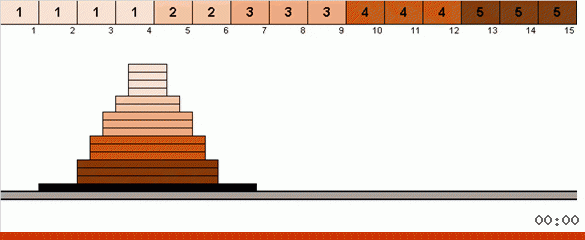
In the simplest case, we are looking for the maximum element in the unported part of the array. When the maximum is found, we make two sharp turns. First, turn the chain of elements so that the maximum is at the opposite end. Then we turn over all unsorted subarray, as a result of which the maximum falls into its place.



Such cordyballets, generally speaking, lead to algorithmic complexity in O ( n ³ ). These trained ciliates tumble in one fell swoop (therefore, the complexity is O ( n ² )), and when programming the reversal of part of the array is an additional cycle.



Pancake sorting is very interesting from a mathematical point of view (the best minds pondered the minimum number of revolutions sufficient for sorting), there are more complex problem statements (with the so-called burnt one side). The topic of pancakes is extremely interesting, perhaps I will write a more detailed monograph on these issues.

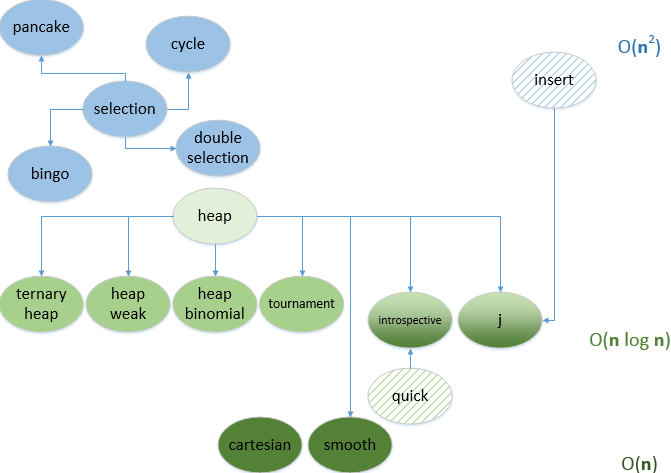
 #   def pancake(data): if len(data) > 1: for size in range(len(data), 1, -1): #      maxindex = max(range(size), key = data.__getitem__) if maxindex + 1 != size: #    ,    if maxindex != 0: #  , #     data[:maxindex+1] = reversed(data[:maxindex+1]) #    , #      data[:size] = reversed(data[:size]) return data 

---

Sorting by selection is only as effective as the search for the minimum / maximum element in the unsorted part of the array. In all algorithms analyzed today, the search is carried out in the form of double enumeration. And double enumeration, whatever one may say, the algorithmic complexity will always be no better than O ( n ² ). Does this mean that all sorts of choices are doomed to mid-quadratic complexity? Not at all, if the search process is organized fundamentally differently. For example, consider the dataset as a heap and search it in the heap. However, the topic of the heap is not even on the article, but on the whole saga, we will certainly talk about the heaps, but at another time.

Links

Selection / Selection , Cycle , Pancake / Pancakes

Articles series:

• Excel application AlgoLab.xlsm
• Exchange sorting
• Sorting inserts
• Sort by selection
  • Binary heap sort and modification
  • Sorting binomial and weak pile
  • Tournament sorting
  • Cartesian sorting
  • Young heap sort
  • Choice sorting comparison
• Merge sort

AlgoLab has added today's bingo, cycle and pancake to the app. In the latter, in connection with drawing the pancakes, a restriction is set - the values ​​of the elements in the array should be from 1 to 5. Of course, you can set more, but the macros will still take numbers from this range in a random order.