Hungarian algorithm, or how mathematics helps in assigning assignments
Hello friends! In this article I would like to tell you about an interesting algorithm from the discipline “Research of operations”, namely about the Hungarian method and how to solve assignment problems with it. I’ll touch on the theory about in which cases and for what tasks this algorithm is applied, step by step I will analyze it on my fictional example, and share my modest sketch of its implementation code in R. Let us proceed!

In order not to paint a lot of theory with mathematical terms and definitions, I propose to consider a couple of options for constructing an assignment problem, and I think you will immediately understand when the Hungarian method is applicable:
As you can see, there are many options for which the Hungarian method is applicable, and similar tasks arise in many areas of activity.
')
As a result, the task must be solved so that one performer (person, machine, instrument, ...) can perform only one job, and each job is performed by only one performer.
A necessary and sufficient condition for solving a problem is its closed type. Those. when the number of performers = the number of jobs (N = M). If this condition is not met, then you can add fictional performers, or fictional works, for which the values in the matrix will be zero. It will not affect the solution of the problem in any way, it will only give it the necessary closed type.
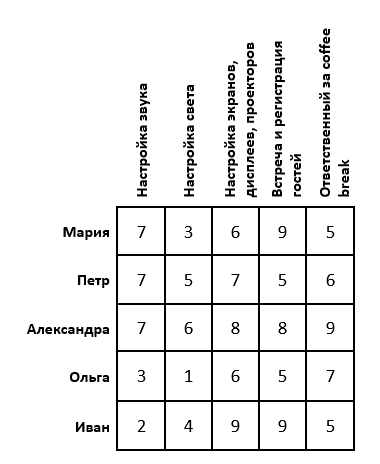
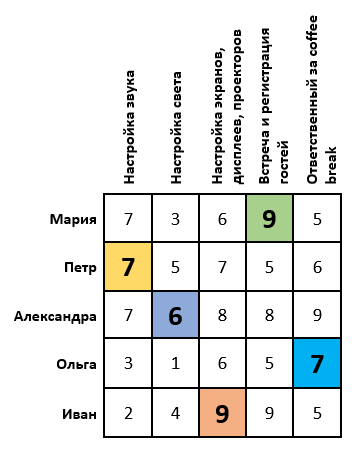
Problem Statement: Let an important scientific conference be scheduled. To conduct it, you need to adjust the sound, light, images, register guests and prepare for the breaks between performances. For this task there are 5 organizers. Each of them has certain estimates of the performance of this or that work (suppose that these estimates are set as an arithmetic average of the feedback from their employees). It is necessary to distribute the organizers so that their total score was maximum. The task is as follows:
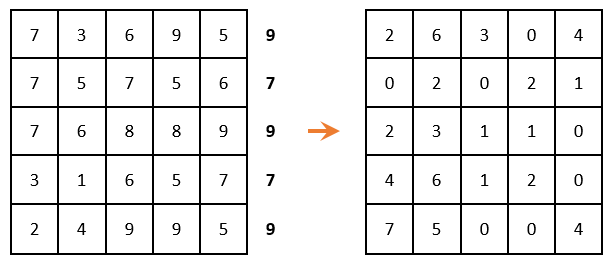
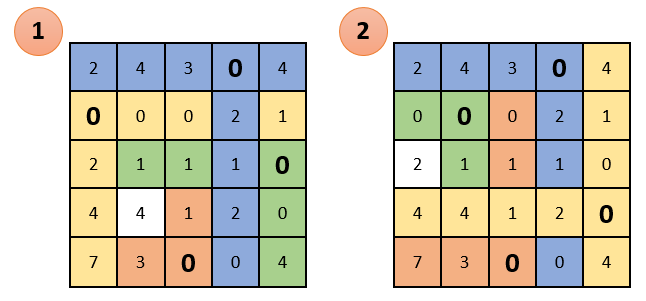
If the problem is solved for a maximum (as in our case), then in each row of the matrix it is necessary to find the maximum element, subtract it from each element of the corresponding row and multiply the entire matrix by -1. If the problem is solved at a minimum, then this step should be skipped.
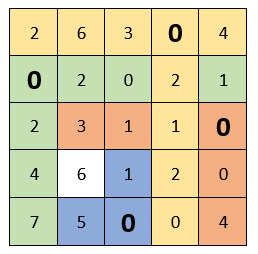
Each row and each column must contain only one selected zero. (i.e., when we chose zero, the remaining zeros in this row or in this column are no longer taken into account). In this case, it is impossible to do this:
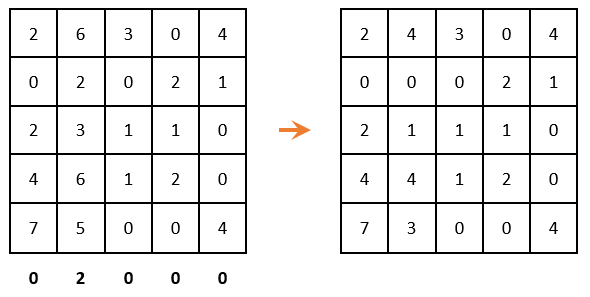
( If the problem is solved at a minimum, then it is necessary to begin with this step ). We continue the decision further. Reduction of the matrix in rows (looking for the minimum element in each row and subtract it from each element, respectively):

Since all minimal elements are zero, the matrix has not changed. We carry out the reduction in columns:
Again, we see that in each column and in each row there is only one selected zero. As can be seen below, in this case it is impossible to do. Presented two options for how to select zeros, but none of them gave the desired result:
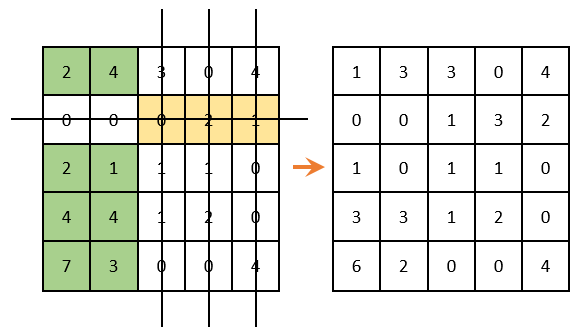
We continue the decision further. We delete the rows and columns that contain zero elements ( IMPORTANT! The number of deletions should be minimal ). Among the remaining elements, we look for the minimum, subtract it from the remaining elements (which are not crossed out) and add to the elements that are located at the intersection of crossed out lines and columns (what is marked in green — there we deduct; what is marked in gold — let's sum it; what is not painted over - do not touch):
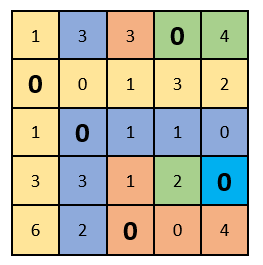
As you can see, in each column and row there is only one selected zero. We complete the solution of the problem!
Substitute in the initial table the location of the selected zeros. Thus, we get the optimum, or the optimal plan, in which the organizers are distributed by work and the sum of marks turned out to be maximum:
If you solve the problem and you still cannot select zeros so that there is only one in each column and row, then we repeat the algorithm from the place where the rows were reduced (the minimum element in each row).
Hungarian algorithm implemented using recursion. I will hope that my code will not cause difficulties. First you need to compile the three functions, and then start the calculations.
The data for solving the problem are taken from the file example.csv which looks like:

The result of the program:

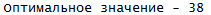
Thank you so much for taking the time to read my article. All references will be provided below. I hope you have learned something new for yourself or updated old knowledge. All success, good luck and good luck!
1. Stormed Wikipedia
2. And other good sites
3. Stressed for myself some information from this article.

A few words about the method
In order not to paint a lot of theory with mathematical terms and definitions, I propose to consider a couple of options for constructing an assignment problem, and I think you will immediately understand when the Hungarian method is applicable:
- The task of appointing employees to positions. It is necessary to distribute the workers to the positions so that maximum efficiency is achieved, or there are minimal expenses for work.
- Appointment of machines on the production section. The distribution of machines so that when their work production was the most profitable, or the cost of maintaining them is minimal.
- Selection of candidates for different vacancies by estimates. This example will be discussed below.
As you can see, there are many options for which the Hungarian method is applicable, and similar tasks arise in many areas of activity.
')
As a result, the task must be solved so that one performer (person, machine, instrument, ...) can perform only one job, and each job is performed by only one performer.
A necessary and sufficient condition for solving a problem is its closed type. Those. when the number of performers = the number of jobs (N = M). If this condition is not met, then you can add fictional performers, or fictional works, for which the values in the matrix will be zero. It will not affect the solution of the problem in any way, it will only give it the necessary closed type.
Step-by-step algorithm by example
Problem Statement: Let an important scientific conference be scheduled. To conduct it, you need to adjust the sound, light, images, register guests and prepare for the breaks between performances. For this task there are 5 organizers. Each of them has certain estimates of the performance of this or that work (suppose that these estimates are set as an arithmetic average of the feedback from their employees). It is necessary to distribute the organizers so that their total score was maximum. The task is as follows:

If the problem is solved for a maximum (as in our case), then in each row of the matrix it is necessary to find the maximum element, subtract it from each element of the corresponding row and multiply the entire matrix by -1. If the problem is solved at a minimum, then this step should be skipped.

Each row and each column must contain only one selected zero. (i.e., when we chose zero, the remaining zeros in this row or in this column are no longer taken into account). In this case, it is impossible to do this:

( If the problem is solved at a minimum, then it is necessary to begin with this step ). We continue the decision further. Reduction of the matrix in rows (looking for the minimum element in each row and subtract it from each element, respectively):

Since all minimal elements are zero, the matrix has not changed. We carry out the reduction in columns:

Again, we see that in each column and in each row there is only one selected zero. As can be seen below, in this case it is impossible to do. Presented two options for how to select zeros, but none of them gave the desired result:

We continue the decision further. We delete the rows and columns that contain zero elements ( IMPORTANT! The number of deletions should be minimal ). Among the remaining elements, we look for the minimum, subtract it from the remaining elements (which are not crossed out) and add to the elements that are located at the intersection of crossed out lines and columns (what is marked in green — there we deduct; what is marked in gold — let's sum it; what is not painted over - do not touch):

As you can see, in each column and row there is only one selected zero. We complete the solution of the problem!

Substitute in the initial table the location of the selected zeros. Thus, we get the optimum, or the optimal plan, in which the organizers are distributed by work and the sum of marks turned out to be maximum:

If you solve the problem and you still cannot select zeros so that there is only one in each column and row, then we repeat the algorithm from the place where the rows were reduced (the minimum element in each row).
Implementation in the R programming language
Hungarian algorithm implemented using recursion. I will hope that my code will not cause difficulties. First you need to compile the three functions, and then start the calculations.
The data for solving the problem are taken from the file example.csv which looks like:

The code added to the spoiler for the article would be too big because of him
# library(dplyr) # csv ( - ; - ) table <- read.csv("example.csv",header=TRUE,row.names=1,sep=";") # unique_index <- hungarian_algorithm(table,T) # cat(paste(row.names(table[as.vector(unique_index$row),])," - ",names(table[as.vector(unique_index$col)])),sep = "\n") # cat(" -",sum(mapply(function(i, j) table[i, j], unique_index$row, unique_index$col, SIMPLIFY = TRUE))) #____________________ __________________________________ hungarian_algorithm <- function(data,optim=F){ # optim = T, if(optim==T) { data <- data %>% apply(1,function(x) (x-max(x))*(-1)) %>% t() %>% as.data.frame() optim <- F } # data <- data %>% apply(1,function(x) x-min(x)) %>% t() %>% as.data.frame() # zero_index <- which(data==0, arr.ind = T) # "" - unique_index <- from_the_beginning(zero_index) # "" , .. if(nrow(unique_index)!=nrow(data)) #.. "" - unique_index <- from_the_end(zero_index) # , if(nrow(unique_index)!=nrow(data)) { # data <- data %>% apply(2,function(x) x-min(x)) %>% as.data.frame() zero_index <- which(data==0, arr.ind = T) unique_index <- from_the_beginning(zero_index) if(nrow(unique_index)!=nrow(data)) unique_index <- from_the_end(zero_index) if(nrow(unique_index)!=nrow(data)) { #"" (! ) index <- which(apply(data,1,function(x) length(x[x==0])>1)) index2 <- which(apply(data[-index,],2,function(x) length(x[x==0])>0)) # min_from_table <- min(data[-index,-index2]) # data[-index,-index2] <- data[-index,-index2]-min_from_table # , data[index,index2] <- data[index,index2]+min_from_table zero_index <- which(data==0, arr.ind = T) unique_index <- from_the_beginning(zero_index) if(nrow(unique_index)!=nrow(data)) unique_index <- from_the_end(zero_index) # "" , .. if(nrow(unique_index)!=nrow(data)) #.. hungarian_algorithm(data,optim) else # "" unique_index } else # "" unique_index } else # "" unique_index } #_________________________________________________________________________________ #__________ "" -___________ from_the_beginning <- function(x,i=0,j=0,index = data.frame(row=numeric(),col=numeric())){ # , i, j find_zero <- x[(!x[,1] %in% i) & (!x[,2] %in% j),] if(length(find_zero)>2){ # i <- c(i,as.vector(find_zero[1,1])) # j <- c(j,as.vector(find_zero[1,2])) # data frame ( ) index <- rbind(index,setNames(as.list(find_zero[1,]), names(index))) # from_the_beginning(find_zero,i,j,index)} else rbind(index,find_zero) } #_________________________________________________________________________________ #__________ "" -___________ from_the_end <- function(x,i=0,j=0,index = data.frame(row=numeric(),col=numeric())){ find_zero <- x[(!x[,1] %in% i) & (!x[,2] %in% j),] if(length(find_zero)>2){ i <- c(i,as.vector(find_zero[nrow(find_zero),1])) j <- c(j,as.vector(find_zero[nrow(find_zero),2])) index <- rbind(index,setNames(as.list(find_zero[nrow(find_zero),]), names(index))) from_the_end(find_zero,i,j,index)} else rbind(index,find_zero) } #_________________________________________________________________________________ The result of the program:

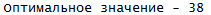
In conclusion
Thank you so much for taking the time to read my article. All references will be provided below. I hope you have learned something new for yourself or updated old knowledge. All success, good luck and good luck!
Resources used
1. Stormed Wikipedia
2. And other good sites
3. Stressed for myself some information from this article.
Source: https://habr.com/ru/post/422009/
All Articles