Confidential transactions in Monero, or how to transfer it is not known what is unknown where
We continue our cycle about the Monero blockchain device, and today's article will be devoted to the Ring Confidential Transactions protocol, which contains confidential transactions and new ring signatures. Unfortunately, there is little information on the Internet about how it works, and we tried to fill this gap.

We will talk about how with this protocol the network hides the transfer amounts, why it abandoned the classic cryptonote ring signatures and how this technology will develop further.
')
Since this protocol is one of the most sophisticated technologies in Monero, the reader will need basic knowledge about the device of this blockchain and superficial knowledge of cryptography on elliptic curves (to refresh this knowledge, you can read the first chapters of our previous article on multi-signatures ).
One of the possible attacks on cryptonote currency is blockchain analysis based on knowledge of the amount and time of the sent transaction. This allows Significantly narrow the search for intruders interested in. To protect against this analysis, an anonymous transaction protocol was implemented in Monero, which completely hides the amount of transfers in the network.
It is worth noting that the idea of hiding amounts is not new. One of the first to describe it was Bitcoin Core developer Greg Maxwell in his article Confidential Transactions . The current implementation of the RingCT is a modification of it with the possibility of using ring signatures (to some extent without them), and so it got its name - the Ring Confidential Transactions.
Among other things, the protocol helps to get rid of problems with mixing dust outputs - outputs of a small amount (usually obtained as surrender from transactions), which created more problems than they cost.
In January 2017, the Monforo hardfork network took place, allowing the optional use of confidential transactions. And in September of the same year with hardforka version 6, such transactions were the only ones allowed in the network.
RingCT uses several mechanisms at once: Multilayered Spontaneous Anonymous Group Signatures (Multilayered Linkable Spontaneous Anonymous Group Signature, hereinafter referred to as MLSAG), the Pedersen Commitments commitment scheme and range proofs (this term does not have a Russian translation).
The RingCT protocol introduces two types of anonymous transactions: simple and full. The first wallet generates when the transaction uses more than one input, the second - in the opposite situation. They differ in the validation of transaction amounts and data signed by the MLSAG-signature (we'll talk more about this below). Moreover, transactions of the type full can be generated with any number of inputs, there is no fundamental difference. The book “Zero to Monero” on this occasion states that the decision to limit full transactions to one input was made in haste and may change in the future.
Recall what transaction inputs are signed in. Each transaction spends some money and generates. The funds are generated by creating transaction outlets (the direct analogy is banknotes), and the output that a transaction spends (after all, in real life, we spend banknotes) becomes an input (be careful, it is very easy to get confused).
An entry refers to several exits, but only spends one, thus creating a “smoke screen” to make it difficult to analyze the history of transfers. If a transaction has more than one input, then such a structure can be represented as a matrix, where the rows are the inputs, and the columns are the kneaded outputs. To prove to the network that the transaction spends its own exits (knows their secret keys), the inputs are signed with a ring signature. Such a signature provides a guarantee that the signer knew the secret keys from all the elements of any of the columns.
Confidential transactions no longer use cryptonote ring signatures that are traditional for cryptonote , they were replaced by the MLSAG — the version of similar single-layer ring signatures, LSAG , adapted for several inputs.
They are called multilayered because they sign several entrances at once, each of which is mixed with several others, that is, a matrix is signed, and not just one row. As we will see later, this helps save on signature size.
Let's take a look at how a ring signature is formed, using the example of a transaction that spends 2 real outputs and uses m - 1 random ones from the blockchain to mix. Denote the public keys of the outputs that we spend as
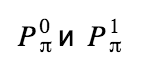 , and key images for them respectively:
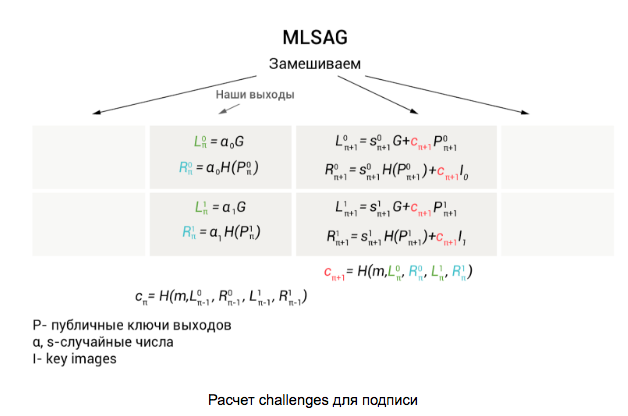
, and key images for them respectively: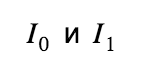 Thus, we have a matrix of 2 x m in size. First we need to calculate the so-called challenges for each pair of exits:
Thus, we have a matrix of 2 x m in size. First we need to calculate the so-called challenges for each pair of exits:
Calculations start with exits that we spend using their public keys: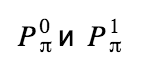 and random numbers
and random numbers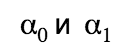 As a result, we get the values:
As a result, we get the values:
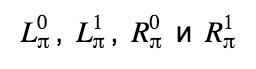 that we use to calculate the challenge
that we use to calculate the challenge
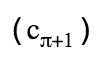 the next pair of outputs (to make it easier to understand that where we are inserting, we have highlighted these values in different colors) All the following values are calculated in a circle using the formulas given in the first illustration. The last is the challenge for a pair of real exits.
the next pair of outputs (to make it easier to understand that where we are inserting, we have highlighted these values in different colors) All the following values are calculated in a circle using the formulas given in the first illustration. The last is the challenge for a pair of real exits.
As we can see, in all columns, except those containing real outputs, randomly generated numbers are used.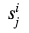 . For the πth column, we also need them. Transform
. For the πth column, we also need them. Transform 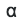 in s:
in s: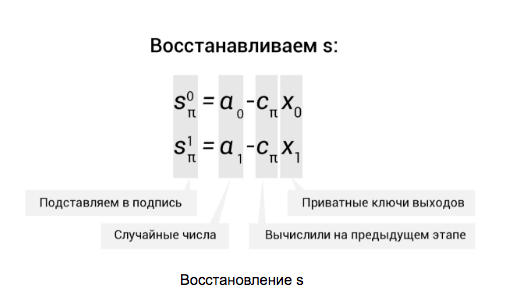
The signature itself is a tuple of all these values:
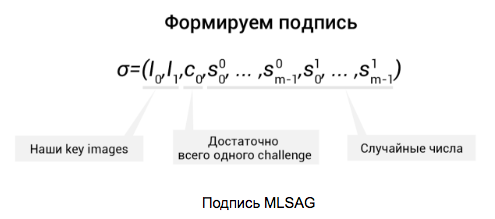
Further, these data are recorded in the transaction.
As we can see, the MLSAG contains only one challenge c 0 , which saves on the size of the signature (which already requires a lot of space). Further, any verifier using data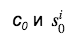 , restores the values c 1 , ..., c m and checks that
, restores the values c 1 , ..., c m and checks that  . Thus, our ring was closed and the signature was tested.
. Thus, our ring was closed and the signature was tested.
For RingCT transactions of type full, one more line is added to the matrix with mixed outputs, but we will tell about it below.
Commitment schemes (often use the English term “commitments”) are used so that one party can prove that it knows a certain secret (number) without actually revealing it. For example, you throw a certain number on your bones, consider a commitment and transfer it to the verifier. Thus, at the time of disclosure of the secret number, the verifier independently considers the commitment, thereby making sure that you did not deceive him.
Monero commitments are used to conceal the amount of transfers and use the most common option - Pedersen commitments. By the way, a curious fact - at first, developers suggested hiding amounts by ordinary mixing, that is, adding outputs for arbitrary amounts to introduce uncertainty, but then switched to commitments (it’s not a fact that they saved on transaction size, as we will see below).
In general, the commitment is as follows:
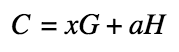 Where C is the value of the commitment itself, a is the hidden sum, H is a fixed point on an elliptic curve (additional generator), and x is some arbitrary mask that hides a factor that is generated randomly. The mask here is needed so that a third party could not simply search for the commitment value.
Where C is the value of the commitment itself, a is the hidden sum, H is a fixed point on an elliptic curve (additional generator), and x is some arbitrary mask that hides a factor that is generated randomly. The mask here is needed so that a third party could not simply search for the commitment value.
When generating a new exit, the wallet calculates a commitment for it, and when it is spent, it takes either the value calculated during the generation or recalculates it again, depending on the type of transaction.
In the case of simple RingCT transactions, in order to ensure that the transaction created outputs for an amount equal to the sum of the inputs (did not make money out of thin air), it is necessary that the sum of commitments of the first and second be the same, that is:
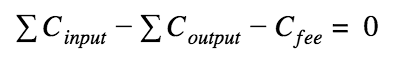
Commitment fees are considered a little different - without a mask:
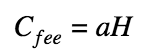 where a is the commission amount, it is publicly available.
where a is the commission amount, it is publicly available.
This approach allows us to prove to the relying party that we use the same amounts without disclosing them.
To make everything clearer, let's look at an example. Suppose a transaction spends two outputs (that is, they become inputs) on 10 and 5 XMR and generates three outputs on the sum of 12 XMR: 3, 4 and 5 XMR. At the same time pays a commission of 3 XMR. Thus, the amount of money spent plus the amount generated and the commission are 15 XMR. Let's try to calculate commitments and look at the difference between their sums (recall the math):

Here we see that the equation comes together - the sums of the input and output masks we need are the same. To do this, the wallet generates randomly x 1 , y 1 , y 2 and y 3 , and the remaining x 2 calculates as follows:
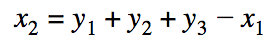
Using these masks, we can prove to any verifier that we do not generate more money than we spend without disclosing the amount. Original, right?
In full RingCT transactions, the verification of transfer amounts is somewhat more intricate. In these transactions, the wallet does not recalculate commitments for entries, but uses those calculated when they are generated. In this case, we must assume that the difference between the amounts we will not get equal to zero, but instead:
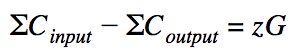
Here, z is the difference between the input and output masks. If we consider zG as a public key (which it is in fact de facto), then z is a private key. Thus, we know the public and corresponding private keys. Having this data, we can use it in the MLSAG ring signature along with the public keys of the kneaded outputs:
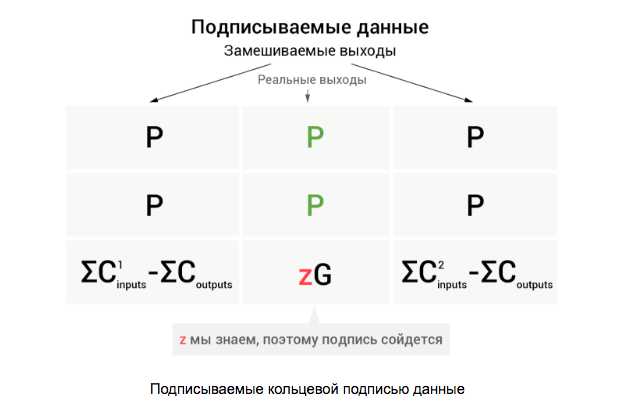
Thus, a valid ring signature will ensure that we know all the private keys of one of the columns, and we can know the private key in the last row only if the transaction does not generate more money than it spends. By the way, here is the answer to the question “why the difference between the sum of commitments here does not lead to zero” - if zG = 0 , then we will open a column with real outputs.
But how does the recipient of the funds know how much money they sent him? Everything is simple here - the sender of the transaction and the recipient exchange keys using the Diffie-Hellman protocol, using the transaction key and the receiver's view key and calculate the shared secret. The sender writes in the special fields of the transaction data on the amounts of the outputs, encrypted with this shared key.
And what will happen if the negative number is used as the sum in the commitments? This may lead to the generation of additional coins! Such an outcome is unacceptable, so we need a guarantee that the amounts we use are not negative (without disclosing these amounts, of course, otherwise so much labor and all for nothing). In other words, we must prove that the sum is in the interval [0, 2 n - 1] .
For this, the amount of each output is divided into binary digits and is considered a commitment for each category separately. As this happens, it is better to look at an example.
Suppose that we have small amounts and are placed in 4 bits (in practice, this is 64 bits), and we create an output of 5 XMR. We count commitments for each grade and total commitment for the full amount:
Then each commitment is mixed with a surrogate (C i -2 i H) and signed in pairs by a ring signature of Borromeo (another ring signature) proposed by Greg Maxwell in 2015 (you can read more about it here ):
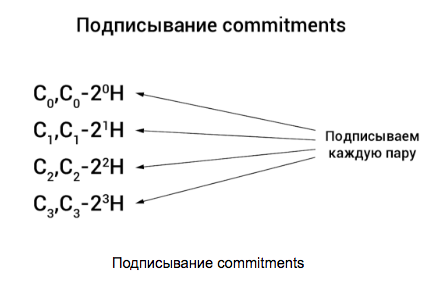 All together, this is called range proof and ensures that commitments use sums in the interval [0, 2 n - 1] .
All together, this is called range proof and ensures that commitments use sums in the interval [0, 2 n - 1] .
In the current implementation, range proofs take up a lot of space - 6176 bytes per output. This leads to large transactions and, consequently, higher commissions. To reduce the size of the transaction, Monero developers introduce instead of Borromeo signatures bulletproofs - a range proof mechanism without bitwise commitments. By some estimates , they are able to reduce the size of range proof to 94%. By the way, in mid-July, the technology was audited by Kudelski Security, which did not reveal significant shortcomings in both the technology itself and its implementation. The technology is already used in the test network, and with the new hard forks it can probably move to the main network.
Ask your questions, suggest topics for new articles about cryptocurrency technologies, and subscribe to our group on Facebook to keep up with our events and publications.

We will talk about how with this protocol the network hides the transfer amounts, why it abandoned the classic cryptonote ring signatures and how this technology will develop further.
')
Since this protocol is one of the most sophisticated technologies in Monero, the reader will need basic knowledge about the device of this blockchain and superficial knowledge of cryptography on elliptic curves (to refresh this knowledge, you can read the first chapters of our previous article on multi-signatures ).
RingCT protocol
One of the possible attacks on cryptonote currency is blockchain analysis based on knowledge of the amount and time of the sent transaction. This allows Significantly narrow the search for intruders interested in. To protect against this analysis, an anonymous transaction protocol was implemented in Monero, which completely hides the amount of transfers in the network.
It is worth noting that the idea of hiding amounts is not new. One of the first to describe it was Bitcoin Core developer Greg Maxwell in his article Confidential Transactions . The current implementation of the RingCT is a modification of it with the possibility of using ring signatures (to some extent without them), and so it got its name - the Ring Confidential Transactions.
Among other things, the protocol helps to get rid of problems with mixing dust outputs - outputs of a small amount (usually obtained as surrender from transactions), which created more problems than they cost.
In January 2017, the Monforo hardfork network took place, allowing the optional use of confidential transactions. And in September of the same year with hardforka version 6, such transactions were the only ones allowed in the network.
RingCT uses several mechanisms at once: Multilayered Spontaneous Anonymous Group Signatures (Multilayered Linkable Spontaneous Anonymous Group Signature, hereinafter referred to as MLSAG), the Pedersen Commitments commitment scheme and range proofs (this term does not have a Russian translation).
The RingCT protocol introduces two types of anonymous transactions: simple and full. The first wallet generates when the transaction uses more than one input, the second - in the opposite situation. They differ in the validation of transaction amounts and data signed by the MLSAG-signature (we'll talk more about this below). Moreover, transactions of the type full can be generated with any number of inputs, there is no fundamental difference. The book “Zero to Monero” on this occasion states that the decision to limit full transactions to one input was made in haste and may change in the future.
MLSAG signature
Recall what transaction inputs are signed in. Each transaction spends some money and generates. The funds are generated by creating transaction outlets (the direct analogy is banknotes), and the output that a transaction spends (after all, in real life, we spend banknotes) becomes an input (be careful, it is very easy to get confused).
An entry refers to several exits, but only spends one, thus creating a “smoke screen” to make it difficult to analyze the history of transfers. If a transaction has more than one input, then such a structure can be represented as a matrix, where the rows are the inputs, and the columns are the kneaded outputs. To prove to the network that the transaction spends its own exits (knows their secret keys), the inputs are signed with a ring signature. Such a signature provides a guarantee that the signer knew the secret keys from all the elements of any of the columns.
Confidential transactions no longer use cryptonote ring signatures that are traditional for cryptonote , they were replaced by the MLSAG — the version of similar single-layer ring signatures, LSAG , adapted for several inputs.
They are called multilayered because they sign several entrances at once, each of which is mixed with several others, that is, a matrix is signed, and not just one row. As we will see later, this helps save on signature size.
Let's take a look at how a ring signature is formed, using the example of a transaction that spends 2 real outputs and uses m - 1 random ones from the blockchain to mix. Denote the public keys of the outputs that we spend as
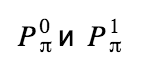
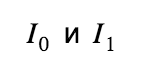

Calculations start with exits that we spend using their public keys:
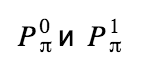
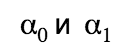
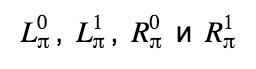
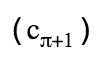
As we can see, in all columns, except those containing real outputs, randomly generated numbers are used.
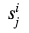 . For the πth column, we also need them. Transform
. For the πth column, we also need them. Transform 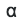 in s:
in s:
The signature itself is a tuple of all these values:

Further, these data are recorded in the transaction.
As we can see, the MLSAG contains only one challenge c 0 , which saves on the size of the signature (which already requires a lot of space). Further, any verifier using data
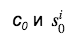 , restores the values c 1 , ..., c m and checks that
, restores the values c 1 , ..., c m and checks that  . Thus, our ring was closed and the signature was tested.
. Thus, our ring was closed and the signature was tested.For RingCT transactions of type full, one more line is added to the matrix with mixed outputs, but we will tell about it below.
Pedersen commitments
Commitment schemes (often use the English term “commitments”) are used so that one party can prove that it knows a certain secret (number) without actually revealing it. For example, you throw a certain number on your bones, consider a commitment and transfer it to the verifier. Thus, at the time of disclosure of the secret number, the verifier independently considers the commitment, thereby making sure that you did not deceive him.
Monero commitments are used to conceal the amount of transfers and use the most common option - Pedersen commitments. By the way, a curious fact - at first, developers suggested hiding amounts by ordinary mixing, that is, adding outputs for arbitrary amounts to introduce uncertainty, but then switched to commitments (it’s not a fact that they saved on transaction size, as we will see below).
In general, the commitment is as follows:
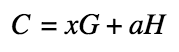
When generating a new exit, the wallet calculates a commitment for it, and when it is spent, it takes either the value calculated during the generation or recalculates it again, depending on the type of transaction.
RingCT simple
In the case of simple RingCT transactions, in order to ensure that the transaction created outputs for an amount equal to the sum of the inputs (did not make money out of thin air), it is necessary that the sum of commitments of the first and second be the same, that is:
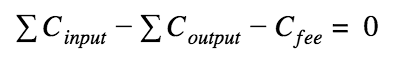
Commitment fees are considered a little different - without a mask:
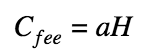
This approach allows us to prove to the relying party that we use the same amounts without disclosing them.
To make everything clearer, let's look at an example. Suppose a transaction spends two outputs (that is, they become inputs) on 10 and 5 XMR and generates three outputs on the sum of 12 XMR: 3, 4 and 5 XMR. At the same time pays a commission of 3 XMR. Thus, the amount of money spent plus the amount generated and the commission are 15 XMR. Let's try to calculate commitments and look at the difference between their sums (recall the math):

Here we see that the equation comes together - the sums of the input and output masks we need are the same. To do this, the wallet generates randomly x 1 , y 1 , y 2 and y 3 , and the remaining x 2 calculates as follows:
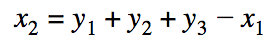
Using these masks, we can prove to any verifier that we do not generate more money than we spend without disclosing the amount. Original, right?
Ringct full
In full RingCT transactions, the verification of transfer amounts is somewhat more intricate. In these transactions, the wallet does not recalculate commitments for entries, but uses those calculated when they are generated. In this case, we must assume that the difference between the amounts we will not get equal to zero, but instead:
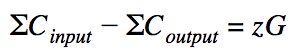
Here, z is the difference between the input and output masks. If we consider zG as a public key (which it is in fact de facto), then z is a private key. Thus, we know the public and corresponding private keys. Having this data, we can use it in the MLSAG ring signature along with the public keys of the kneaded outputs:

Thus, a valid ring signature will ensure that we know all the private keys of one of the columns, and we can know the private key in the last row only if the transaction does not generate more money than it spends. By the way, here is the answer to the question “why the difference between the sum of commitments here does not lead to zero” - if zG = 0 , then we will open a column with real outputs.
But how does the recipient of the funds know how much money they sent him? Everything is simple here - the sender of the transaction and the recipient exchange keys using the Diffie-Hellman protocol, using the transaction key and the receiver's view key and calculate the shared secret. The sender writes in the special fields of the transaction data on the amounts of the outputs, encrypted with this shared key.
Range proofs
And what will happen if the negative number is used as the sum in the commitments? This may lead to the generation of additional coins! Such an outcome is unacceptable, so we need a guarantee that the amounts we use are not negative (without disclosing these amounts, of course, otherwise so much labor and all for nothing). In other words, we must prove that the sum is in the interval [0, 2 n - 1] .
For this, the amount of each output is divided into binary digits and is considered a commitment for each category separately. As this happens, it is better to look at an example.
Suppose that we have small amounts and are placed in 4 bits (in practice, this is 64 bits), and we create an output of 5 XMR. We count commitments for each grade and total commitment for the full amount:

Then each commitment is mixed with a surrogate (C i -2 i H) and signed in pairs by a ring signature of Borromeo (another ring signature) proposed by Greg Maxwell in 2015 (you can read more about it here ):

What's next?
In the current implementation, range proofs take up a lot of space - 6176 bytes per output. This leads to large transactions and, consequently, higher commissions. To reduce the size of the transaction, Monero developers introduce instead of Borromeo signatures bulletproofs - a range proof mechanism without bitwise commitments. By some estimates , they are able to reduce the size of range proof to 94%. By the way, in mid-July, the technology was audited by Kudelski Security, which did not reveal significant shortcomings in both the technology itself and its implementation. The technology is already used in the test network, and with the new hard forks it can probably move to the main network.
Ask your questions, suggest topics for new articles about cryptocurrency technologies, and subscribe to our group on Facebook to keep up with our events and publications.
Source: https://habr.com/ru/post/421913/
All Articles