The theory of happiness. The curse of the director and damn printers
I continue to acquaint Habr's readers with chapters from my book “The Theory of Happiness” with the subtitle “Mathematical foundations of the laws of meanness”. This is not a published popular science book, very informally telling how mathematics allows you to look at the world and life of people with a new degree of awareness. It is for those who are interested in science and for those who are interested in life. And since our life is complex and, by and large, unpredictable, the emphasis in the book is mainly on probability theory and mathematical statistics. Here theorems are not proved and the fundamentals of science are not given; this is by no means a textbook, but what is called recreational science. But it is this almost playful approach that allows us to develop intuition, brighten up lectures for students with vivid examples, and, finally, explain to nemathematicians and our children what we found so interesting in our dry science.

')
We speculate about timeouts, deadlines, and non-time breaking printers.
In the previous chapter, we talked about random processes. One of the simplest processes requiring a minimum of additional assumptions is the Poisson flow. Let me remind you that it can be implemented by randomly distributing a known number of independent events over a time interval. Good examples can be raindrops hitting the roof, a stream of private cars on the road, strong earthquakes, and the like.
And what will we get if the events cease to be independent, but will form an ordered chain? Let's say in the chain event can only happen after an event and before the event , although the moments at which these events will happen let them remain random. Let's see how these ordered chains will be placed on a limited time interval. We will locate the first event at an arbitrary point, the second is also random, but definitely later than the first, the third after the second and so on. For each next stage there will be less and less time, so by the right side of the interval (before the deadline) there should be a noticeable increase in the intensity of the process. Sooner or later, the time to complete the tasks will end and the chain will end. We call the process we have constructed the stochastic chain with a deadline , and the chosen disorderly strategy of performing the work as a dunce strategy . The figure shows an example of a chain constructed in this way from stages of work, which was released days

An example of a stochastic chain with a deadline. In this case, it was possible to do five cases, you can still have time to do the sixth, and there will not be enough time for seven.
We formulate the problem, taking as a test subject, say, a theater director. Let the director and the company have days for staging a certain action. Preparation is broken into consecutive rehearsal stages, each of which requires one day to perform. What is the probability not to meet the deadline, realizing the process of work performance described by us? If the preparation of the event requires the involvement of different people and different production processes, then lining, illness or simply spleen are possible - all the prerequisites for the realization of our stochastic chain with a deadline.
To begin with, I turned to simulation to find out how the length of chains is distributed, which can be performed in a limited period of time of a given length using the dunner's strategy. That's what happens for :
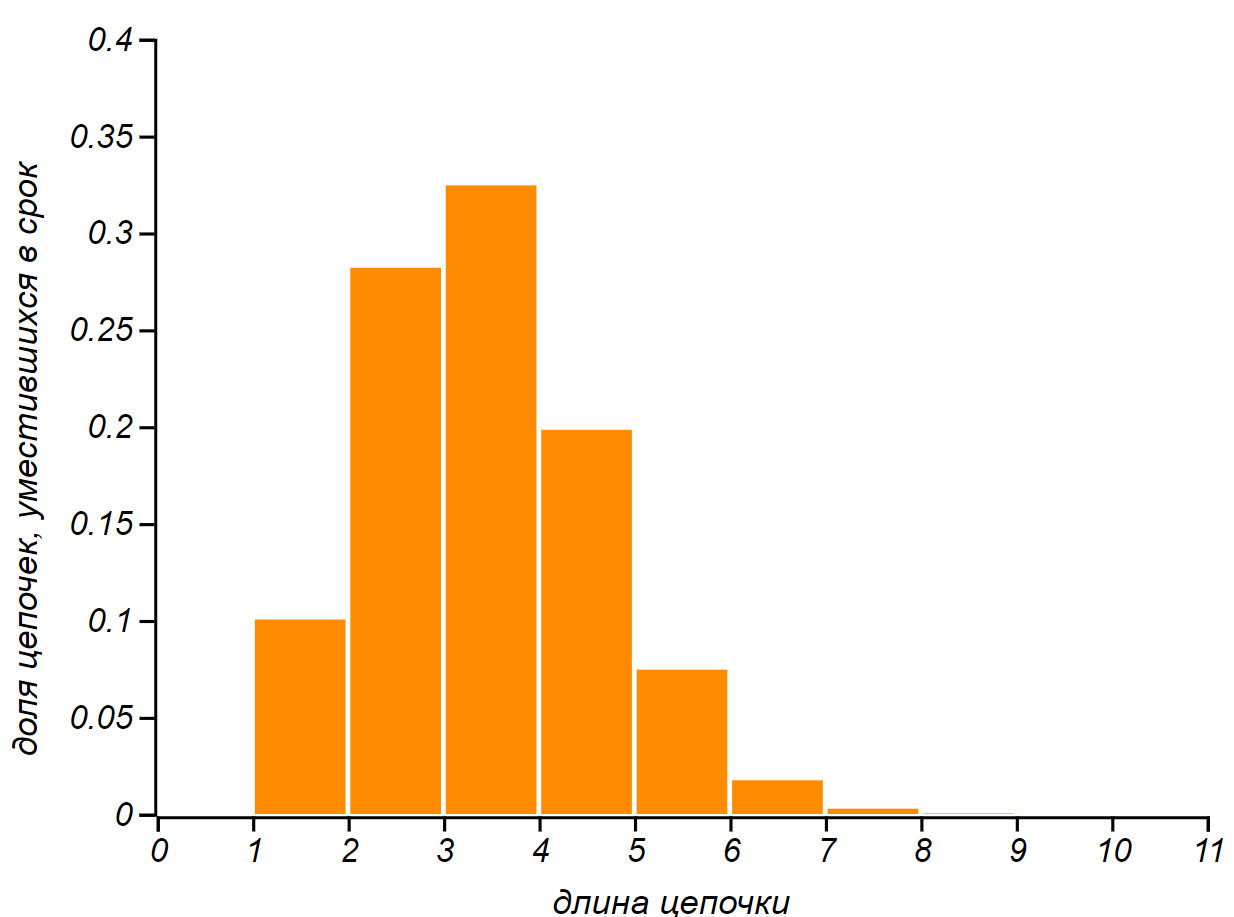
The probability function for the length of the chains that can be done in the allotted time.
This distribution was not found in any reference books on probability theory and mathematical statistics. I managed to get an analytical solution for the probability function in a finite form:
Take another look at the length distribution of the chains. It is evident that the chances of not having time to do one thing are not at all - for him there will always be time. Short chains of two cases make up a tenth of the total - these are unsuccessful chains that began on the last day (out of ten) and did not leave time to continue. The share of very long chains, as expected, is small and decreases with increasing length, almost disappearing. Well, a chain of ten cases is randomly almost impossible to accomplish - the probability of such an outcome is equal to .
To our question: what is the probability not to meet the days having before you successive stages of the task, help answer the distribution function - a cumulative curve for the Stirling distribution. We construct such curves for and corresponding to the week, month, year and (of course, conditionally) of life.
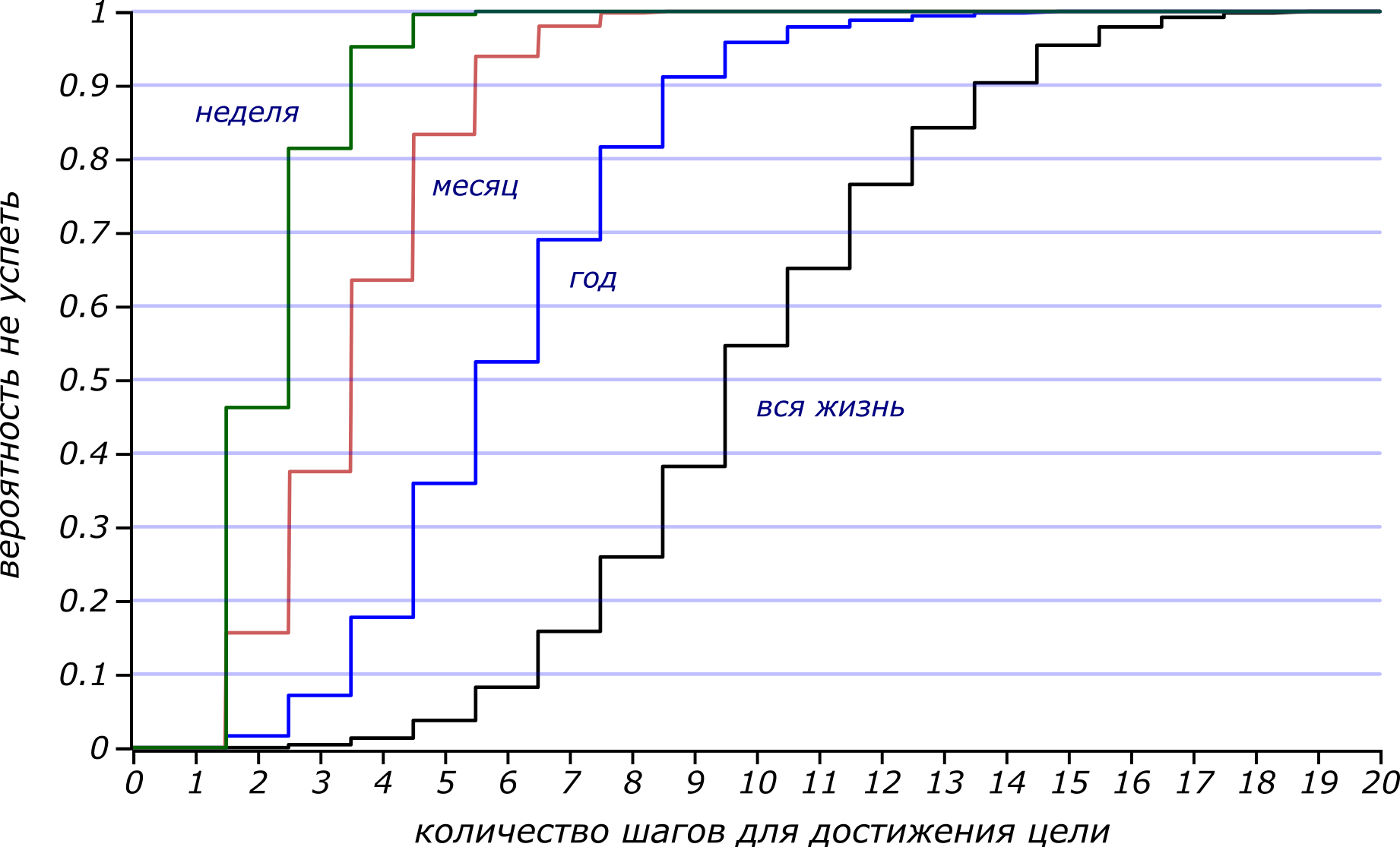
The probability of not having time to complete chains of various lengths at one time or another.
These graphs show that the probability of not meeting the month with a task that has steps exceeds . And that it is better for an unorganized boobies to not plan more than three cases a week, and he will not do a dozen cases, with a probability exceeding and for all my life! We are convinced that with the increase of time by several orders of magnitude, the number of executable cases just increases slightly. Life is so short!
Let us now examine the very phenomenon of time trouble, its exhausting properties. To do this, we construct several thousand stochastic chains and average them in order to get the expected pace of work .
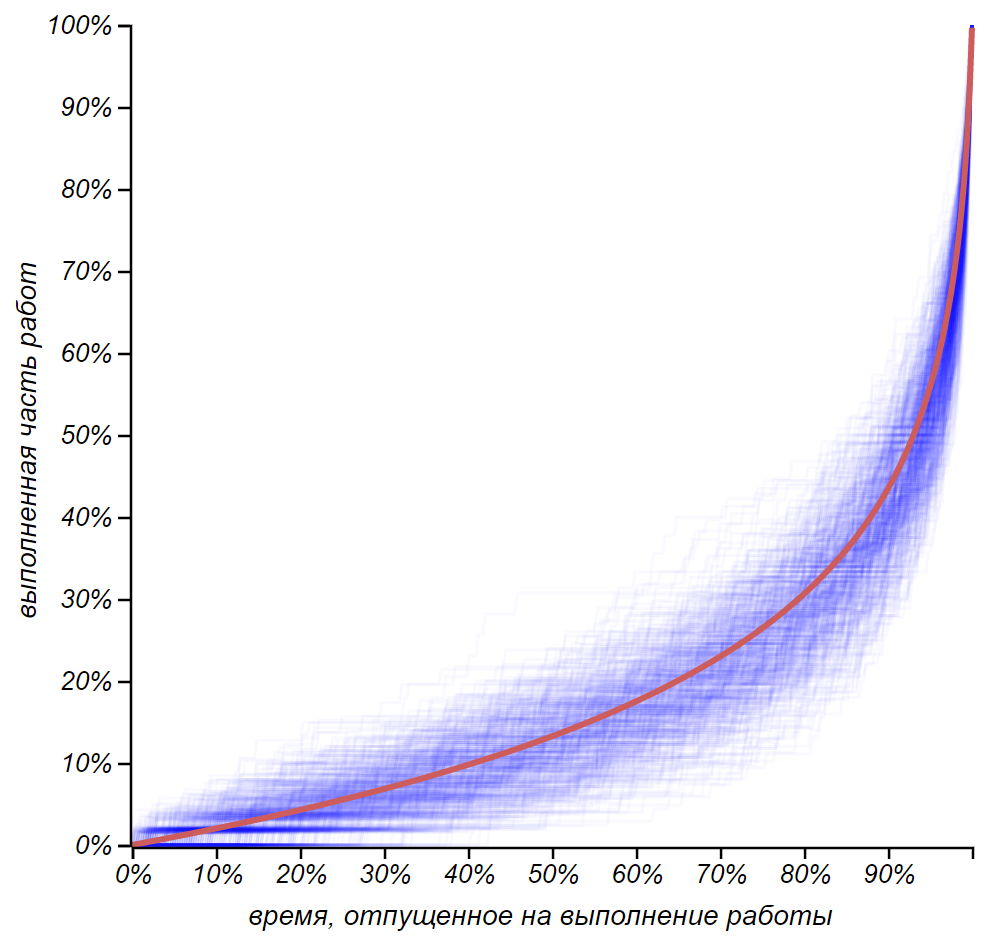
Many stochastic chains with deadlines and the expected pace of work.
Please note that the axis of the graph is given to the total number of cases and all the allotted time. On the one hand, it allows us to compare both different dates and different chains along the length, and on the other, we again received something similar to the Lorenz curve: a kind of formalized reflection of injustice.
The observed pace, alas, is highly uneven: in the first half of the term hardly work, and a good half of all cases will have to be performed, having at my disposal time, but the main feature: the pace, or rather its inclination, is rapidly increasing when approaching the deadline! We received a model of the pre-New Year rage or panic on the eve of the annual report, and also found the law of meanness, familiar to anyone who had to organize a concert, a costume evening or other event:
Excellent living examples of such processes are described, for example, in the stories by Karel Čapek “How a newspaper is made” and “How a play is made” . Is the reason for this curse only in our lack of organization and disorder? These are, of course, the main reasons, but we are not so guilty in it that it was impossible to try to justify oneself with any mathematical law. The dunce's strategy, of course, looks stupid, but the exponential growth rate is not a joke! Is it even possible to cope with it?
The expected pace of work can be calculated accurately. The formula is not very elegant, but it is noteworthy that it includes the number of days and does not include the number of scheduled cases:

The most likely pace of work in a limited time. Interestingly, the hard time limit is beneficial. The name is only a week in stock, we will most likely begin to work evenly (a third of the work will be ready by half time), and if you have a whole year ahead, you can relax, well, and then regret it.
For an ideal perfectionist who performs the work absolutely evenly, the pace of execution should tend to the diagonal (the blue dotted line in the figure). This is similar to the equality curve on the Lorentz diagram, which signifies justice. Just as we calculated the Gini coefficient for the Lorentz diagram, we can, based on the area between the work execution rate curve and the ideal curve, calculate a certain meanness factor, which will show how far we are from the ideal. It depends on the length of the selected period and slowly increases with increasing . In our examples for the week, month and year, the meanness factor is equal, respectively , and .
How to deal with the growing wave of worries and time trouble? You can, for example, pull yourself together. A person with an excellent student syndrome may seek to do the following thing as soon as possible, of course. A plausible model is the choice of moment for the next case, following an exponential distribution with a density inversely proportional to the remaining time. This will not exclude some uncertainty inherent in our lives, but will express the good desire to do all the things as soon as possible. Let's call this strategy a strategy of good intentions . These are the probabilities of the assignments to complete the tasks on time for the adherent of this strategy, who in half of the cases will do the next thing in the first quarter of the remaining time:
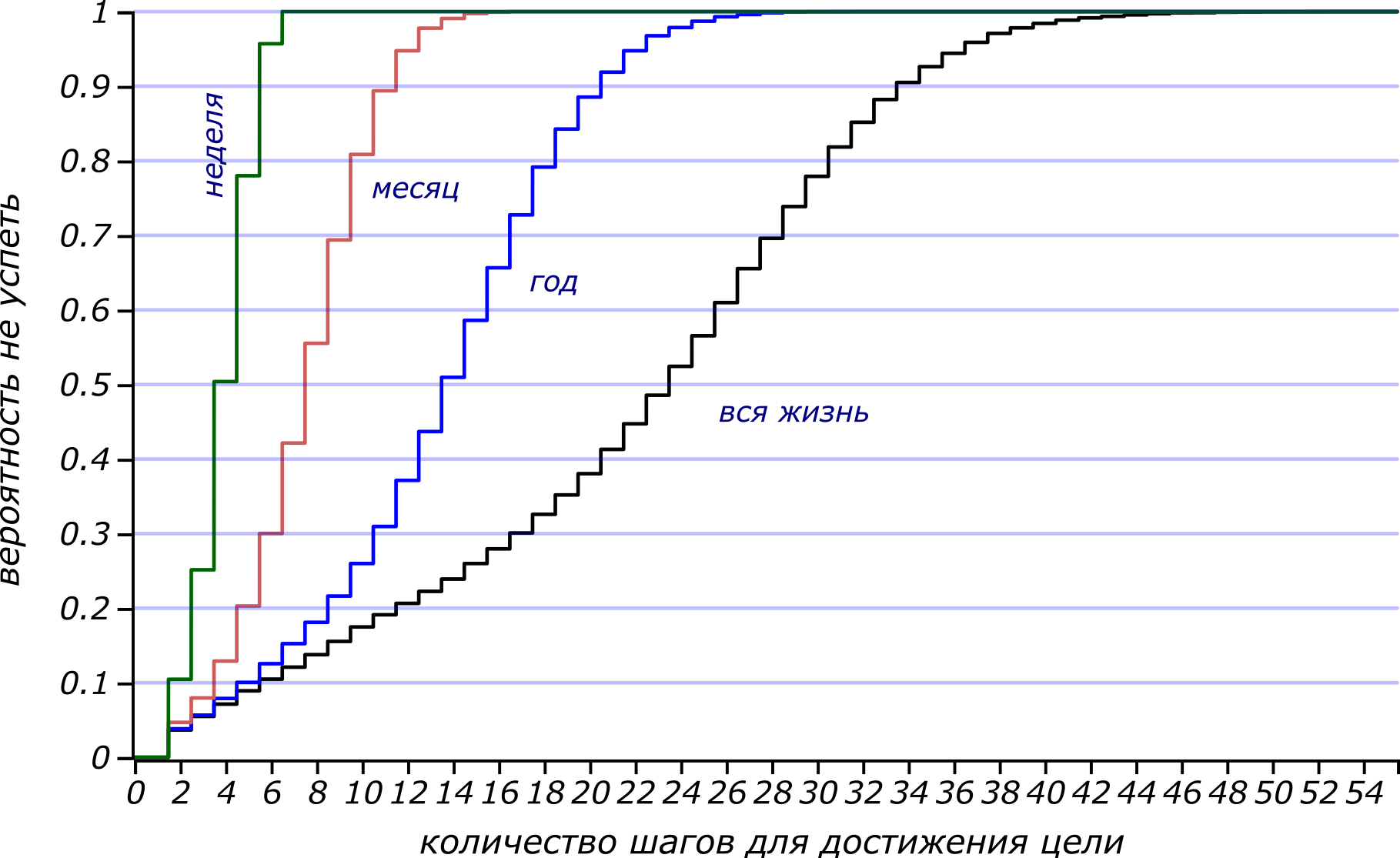
The probability distribution is not to be in time in time for the strategy of good intentions.
Significantly better! With a good chance you can do five things during the week and keep yourself two days off. But still, for larger periods, increasing opportunities is not revolutionary. The problem lies in the fact that the expected number of successfully completed cases still remains proportional to the logarithm of the allotted time, and the logarithm grows extremely slowly! So, planning a lot, you need to keep in mind that the intensity of the process will inevitably increase, and most likely, there will not be enough time on the eve of the deadline. In any case, it is necessary to remember that life is short and in order to have time to realize our plans, you need to act right now!
Let's admire the pace of a well-intentioned high achiever.
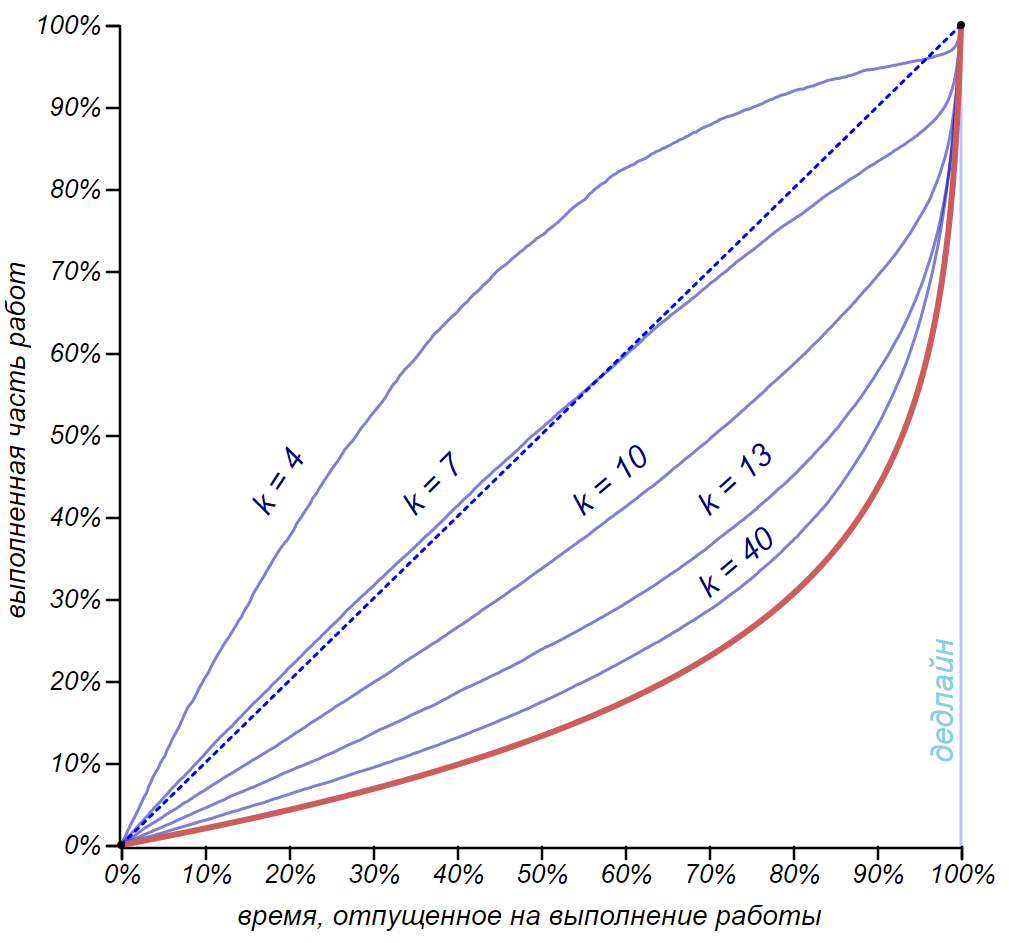
The expected rate of work performance by a methodical person trying to proceed to the next stage of work as soon as possible. The graphs show the results of averaging tens of thousands of numerical experiments that simulate the execution of a task with a fixed number of stages. The red line indicates the maximum rate for a large number of tasks.
Our careful worker was able to distribute the work more evenly, and to do significantly more things, but he was still waiting for time trouble. Such a person will carry out short chains with a significant over-fulfillment of the plan, and a chain of seven cases will be almost perfect. However, as the number of cases grows, the expected pace quickly approaches the theoretical pace obtained with the dunce strategy! Increased overall performance, but the parkin before the deadline did not disappear. So loading can be dokanat and zapravskogo bore!
However, there is another well-known way to significantly discipline the execution of work: instead of one deadline, you need to do a lot of them. Let's divide the deadline for the work into two equal parts and we will adhere to this new deadline, considering it, say, an intermediate report. For each of these parts, we can construct a curve of the expected pace of work, as shown in the figure.
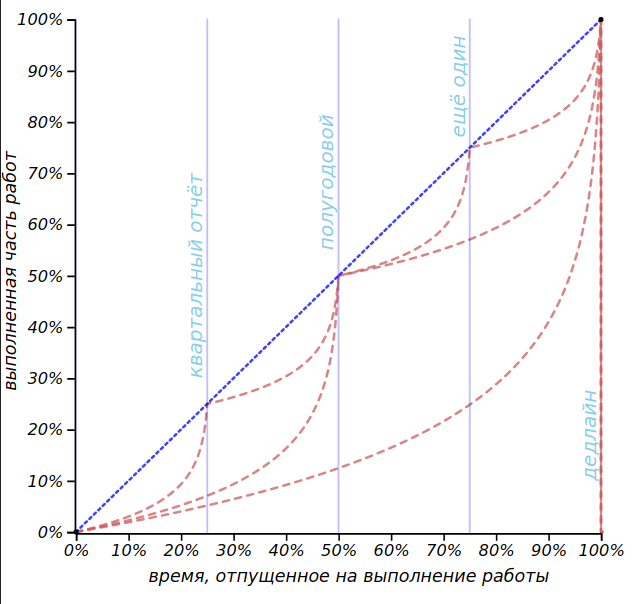 Splitting work time into several intermediate reporting periods allows you to perform the work more evenly, but adds stress as each new report approaches.
Splitting work time into several intermediate reporting periods allows you to perform the work more evenly, but adds stress as each new report approaches.
Despite the hassle of the interim report, we achieved our goal: the area under the overall execution rate curve decreased and the meanness ratio decreased from before . In addition, the reduction in the period (along with the reduction in the number of cases, of course) brings the expected pace of work to an ideal one, so the meanness ratio has more than doubled. Adding two more, say, quarterly reports, will reduce it to , but in so doing we will drive our performers into four stressful periods at once, and they will still suffer loudly, complaining about their fate and their superiors! Well, we can show our calculations to the workers and prove that by introducing quarterly reports, they lowered the coefficient of meanness of their lives five times, if this, of course, will be a consolation to them.
Moreover, if the number of intermediate deadlines is aspired to the number of days allowed for work, the pace of work will be close to the ideal, but very boring pace.
Let's add a couple of words about the strategy of the dunce and the Stirling distribution. The distribution obtained by us shows the probability of obtaining a given number of events in a certain time interval. Counting events in a real Poisson stream with intensity we come to the well-known Poisson distribution:
This conclusion allows us to ask the question: what if we add to the process of performing the chain of affairs we have constructed any rare troubles beyond our control: a blizzard, a terrible traffic jam, a runny nose, a printer breakdown, or a national holiday?
For the Poisson process, a random decimation process is defined, consisting in the fact that with some probability we will begin to delete events from the stream. Accidental thinning with probability leaves the process Poisson, but its intensity decreases, multiplying by . Events corresponding to the coincidence of trouble and any stage of the work themselves form the Poisson process, with significantly less intensity, but in our case, also monotonously and rapidly growing. So fast that no matter how small the probability of trouble, for a sufficiently large number of cases (or the time allotted for work), closer to the deadline, it will increase to quite observable. And the printer will blunt just before the term exchange!
Do not be surprised if the bus breaks exactly when you are already late. The bus does not wish you evil. Simply, if you are a girl, then the sequence of affairs: choose a dress, eat candy, wash, put on the chosen dress, put on makeup, put on a chain, shift things from a handbag to a clutch, clean shoes and so on and so forth goes to the most important and exciting deadline - bye ! And the pace with which you are flying towards the fate is already so crazy that the most unlikely miracles begin to happen.
In the end, but what is a miracle, if not the realization of the incredible!
Published chapters:
• Introduction to Merphology
• Accidents are random?
• dizzying flight of butter sandwich
• The law of watermelon peel and the normality of abnormality
• The law of the zebra and the queue
• The curse of the director and damn printers
• Thermodynamics of class inequality
• Accidents are random?
• dizzying flight of butter sandwich
• The law of watermelon peel and the normality of abnormality
• The law of the zebra and the queue
• The curse of the director and damn printers
• Thermodynamics of class inequality

')
We speculate about timeouts, deadlines, and non-time breaking printers.
Dunce strategy
In the previous chapter, we talked about random processes. One of the simplest processes requiring a minimum of additional assumptions is the Poisson flow. Let me remind you that it can be implemented by randomly distributing a known number of independent events over a time interval. Good examples can be raindrops hitting the roof, a stream of private cars on the road, strong earthquakes, and the like.
And what will we get if the events cease to be independent, but will form an ordered chain? Let's say in the chain event can only happen after an event and before the event , although the moments at which these events will happen let them remain random. Let's see how these ordered chains will be placed on a limited time interval. We will locate the first event at an arbitrary point, the second is also random, but definitely later than the first, the third after the second and so on. For each next stage there will be less and less time, so by the right side of the interval (before the deadline) there should be a noticeable increase in the intensity of the process. Sooner or later, the time to complete the tasks will end and the chain will end. We call the process we have constructed the stochastic chain with a deadline , and the chosen disorderly strategy of performing the work as a dunce strategy . The figure shows an example of a chain constructed in this way from stages of work, which was released days

An example of a stochastic chain with a deadline. In this case, it was possible to do five cases, you can still have time to do the sixth, and there will not be enough time for seven.
We formulate the problem, taking as a test subject, say, a theater director. Let the director and the company have days for staging a certain action. Preparation is broken into consecutive rehearsal stages, each of which requires one day to perform. What is the probability not to meet the deadline, realizing the process of work performance described by us? If the preparation of the event requires the involvement of different people and different production processes, then lining, illness or simply spleen are possible - all the prerequisites for the realization of our stochastic chain with a deadline.
To begin with, I turned to simulation to find out how the length of chains is distributed, which can be performed in a limited period of time of a given length using the dunner's strategy. That's what happens for :

The probability function for the length of the chains that can be done in the allotted time.
This distribution was not found in any reference books on probability theory and mathematical statistics. I managed to get an analytical solution for the probability function in a finite form:
here - the probability of performing a chain of length at lengths of time, and the design denotes the so-called Stirling numbers of the first kind , they arise in combinatorics when counting cyclic permutations. By the right of the discoverer, I will call this distribution the name of Stirling. It was even possible to obtain exact expressions for the mathematical expectation of the length of the chains and their variance:
Here - this is a harmonic number: a partial sum of the divergent harmonic series , but - partial amount of a row . Actually, for the sake of calculating these values, I investigated the resulting distribution. The average length of chains with growth grows very slowly, albeit unlimited. Without making a mistake, we can say that it grows logarithmically. In turn, the variance is not much different from the average, and the added coefficient tends to constant . A little later, this observation will be useful to us.
Take another look at the length distribution of the chains. It is evident that the chances of not having time to do one thing are not at all - for him there will always be time. Short chains of two cases make up a tenth of the total - these are unsuccessful chains that began on the last day (out of ten) and did not leave time to continue. The share of very long chains, as expected, is small and decreases with increasing length, almost disappearing. Well, a chain of ten cases is randomly almost impossible to accomplish - the probability of such an outcome is equal to .
To our question: what is the probability not to meet the days having before you successive stages of the task, help answer the distribution function - a cumulative curve for the Stirling distribution. We construct such curves for and corresponding to the week, month, year and (of course, conditionally) of life.

The probability of not having time to complete chains of various lengths at one time or another.
These graphs show that the probability of not meeting the month with a task that has steps exceeds . And that it is better for an unorganized boobies to not plan more than three cases a week, and he will not do a dozen cases, with a probability exceeding and for all my life! We are convinced that with the increase of time by several orders of magnitude, the number of executable cases just increases slightly. Life is so short!
Faster, faster!
Let us now examine the very phenomenon of time trouble, its exhausting properties. To do this, we construct several thousand stochastic chains and average them in order to get the expected pace of work .

Many stochastic chains with deadlines and the expected pace of work.
Please note that the axis of the graph is given to the total number of cases and all the allotted time. On the one hand, it allows us to compare both different dates and different chains along the length, and on the other, we again received something similar to the Lorenz curve: a kind of formalized reflection of injustice.
The observed pace, alas, is highly uneven: in the first half of the term hardly work, and a good half of all cases will have to be performed, having at my disposal time, but the main feature: the pace, or rather its inclination, is rapidly increasing when approaching the deadline! We received a model of the pre-New Year rage or panic on the eve of the annual report, and also found the law of meanness, familiar to anyone who had to organize a concert, a costume evening or other event:
No matter how much time was allotted for the preparation of the event, most of the cases will remain on the last night!
Excellent living examples of such processes are described, for example, in the stories by Karel Čapek “How a newspaper is made” and “How a play is made” . Is the reason for this curse only in our lack of organization and disorder? These are, of course, the main reasons, but we are not so guilty in it that it was impossible to try to justify oneself with any mathematical law. The dunce's strategy, of course, looks stupid, but the exponential growth rate is not a joke! Is it even possible to cope with it?
The expected pace of work can be calculated accurately. The formula is not very elegant, but it is noteworthy that it includes the number of days and does not include the number of scheduled cases:
Logarithm is a slow function, unless pressed against a wall. In the last days before the deadline, the pace grows catastrophically, at the same rate that the logarithm falls into the abyss as it approaches zero. However, it still depends on the number of days allocated. You can see how the expected pace for the week, month, and year looks like:

The most likely pace of work in a limited time. Interestingly, the hard time limit is beneficial. The name is only a week in stock, we will most likely begin to work evenly (a third of the work will be ready by half time), and if you have a whole year ahead, you can relax, well, and then regret it.
For an ideal perfectionist who performs the work absolutely evenly, the pace of execution should tend to the diagonal (the blue dotted line in the figure). This is similar to the equality curve on the Lorentz diagram, which signifies justice. Just as we calculated the Gini coefficient for the Lorentz diagram, we can, based on the area between the work execution rate curve and the ideal curve, calculate a certain meanness factor, which will show how far we are from the ideal. It depends on the length of the selected period and slowly increases with increasing . In our examples for the week, month and year, the meanness factor is equal, respectively , and .
How to deal with the growing wave of worries and time trouble? You can, for example, pull yourself together. A person with an excellent student syndrome may seek to do the following thing as soon as possible, of course. A plausible model is the choice of moment for the next case, following an exponential distribution with a density inversely proportional to the remaining time. This will not exclude some uncertainty inherent in our lives, but will express the good desire to do all the things as soon as possible. Let's call this strategy a strategy of good intentions . These are the probabilities of the assignments to complete the tasks on time for the adherent of this strategy, who in half of the cases will do the next thing in the first quarter of the remaining time:

The probability distribution is not to be in time in time for the strategy of good intentions.
Significantly better! With a good chance you can do five things during the week and keep yourself two days off. But still, for larger periods, increasing opportunities is not revolutionary. The problem lies in the fact that the expected number of successfully completed cases still remains proportional to the logarithm of the allotted time, and the logarithm grows extremely slowly! So, planning a lot, you need to keep in mind that the intensity of the process will inevitably increase, and most likely, there will not be enough time on the eve of the deadline. In any case, it is necessary to remember that life is short and in order to have time to realize our plans, you need to act right now!
Let's admire the pace of a well-intentioned high achiever.

The expected rate of work performance by a methodical person trying to proceed to the next stage of work as soon as possible. The graphs show the results of averaging tens of thousands of numerical experiments that simulate the execution of a task with a fixed number of stages. The red line indicates the maximum rate for a large number of tasks.
Our careful worker was able to distribute the work more evenly, and to do significantly more things, but he was still waiting for time trouble. Such a person will carry out short chains with a significant over-fulfillment of the plan, and a chain of seven cases will be almost perfect. However, as the number of cases grows, the expected pace quickly approaches the theoretical pace obtained with the dunce strategy! Increased overall performance, but the parkin before the deadline did not disappear. So loading can be dokanat and zapravskogo bore!
However, there is another well-known way to significantly discipline the execution of work: instead of one deadline, you need to do a lot of them. Let's divide the deadline for the work into two equal parts and we will adhere to this new deadline, considering it, say, an intermediate report. For each of these parts, we can construct a curve of the expected pace of work, as shown in the figure.

Despite the hassle of the interim report, we achieved our goal: the area under the overall execution rate curve decreased and the meanness ratio decreased from before . In addition, the reduction in the period (along with the reduction in the number of cases, of course) brings the expected pace of work to an ideal one, so the meanness ratio has more than doubled. Adding two more, say, quarterly reports, will reduce it to , but in so doing we will drive our performers into four stressful periods at once, and they will still suffer loudly, complaining about their fate and their superiors! Well, we can show our calculations to the workers and prove that by introducing quarterly reports, they lowered the coefficient of meanness of their lives five times, if this, of course, will be a consolation to them.
Moreover, if the number of intermediate deadlines is aspired to the number of days allowed for work, the pace of work will be close to the ideal, but very boring pace.
Here you go! Also the printer broke!
Let's add a couple of words about the strategy of the dunce and the Stirling distribution. The distribution obtained by us shows the probability of obtaining a given number of events in a certain time interval. Counting events in a real Poisson stream with intensity we come to the well-known Poisson distribution:
describing confidence to get exactly events in a unit time interval. The expression for the Stirling numbers has an asymptotic expansion, which for large reduces the distribution of lengths of chains with a deadline to a displaced Poisson distribution with intensity . Thus, from the statistical point of view, our stochastic process with deadline can be viewed either as a Poisson process on a condensing time grid, or as a non-uniform Poisson process, the intensity of which is monotonously and rapidly growing. And, strictly speaking, our process is not Poisson, since the events in it are not independent, however, the statistical properties we need are similar. The similarity of the average value and the dispersion of the Stirling distribution noted by me, characteristic of the Poisson distribution, also speaks of their similarity.
This conclusion allows us to ask the question: what if we add to the process of performing the chain of affairs we have constructed any rare troubles beyond our control: a blizzard, a terrible traffic jam, a runny nose, a printer breakdown, or a national holiday?
For the Poisson process, a random decimation process is defined, consisting in the fact that with some probability we will begin to delete events from the stream. Accidental thinning with probability leaves the process Poisson, but its intensity decreases, multiplying by . Events corresponding to the coincidence of trouble and any stage of the work themselves form the Poisson process, with significantly less intensity, but in our case, also monotonously and rapidly growing. So fast that no matter how small the probability of trouble, for a sufficiently large number of cases (or the time allotted for work), closer to the deadline, it will increase to quite observable. And the printer will blunt just before the term exchange!
Do not be surprised if the bus breaks exactly when you are already late. The bus does not wish you evil. Simply, if you are a girl, then the sequence of affairs: choose a dress, eat candy, wash, put on the chosen dress, put on makeup, put on a chain, shift things from a handbag to a clutch, clean shoes and so on and so forth goes to the most important and exciting deadline - bye ! And the pace with which you are flying towards the fate is already so crazy that the most unlikely miracles begin to happen.
In the end, but what is a miracle, if not the realization of the incredible!
Source: https://habr.com/ru/post/421351/
All Articles