The first part (code analysis) is here: https://habr.com/post/420725/ .

Algorithm

Description

The algorithm continuously performs the following steps:

1. Waiting until a new tetrimino is created.
2. Checks the type of the newly created Tetrimino, the type of the next Tetrimino (a figure in the preview field) and the contents of the playing field.
3. Investigates all possible ways to add two tetrimino to the playing field and evaluates each probability.
4. Moves the newly created Tetrimino to match the location of the best detected probability.

Each of these steps is described in detail below.
')

Lock search

Consider a simplified version of Tetris, in which the figures do not fall automatically. The only way to bring the figure down is a soft descent. By removing the timings from the game, we can fully describe the state of the active Tetrimino by its position and orientation. The figure has a known place of initial creation, and the following operations are used to convert from one state to another:

• Move one step down
• Move one step left
• Move one step to the right
• Turn one step counterclockwise
• Rotate one step clockwise

These operations are applicable only when the squares of the resulting tetrimino correspond to empty cells of the playing field. When it is impossible to move one step down, the state is considered to be blocked. However, since we have simplified Tetris and the blocking wait is essentially infinite, the locked state can be further transformed by other operations, performing slips and scrolling.

A set of blocked states with a minimal sequence of operations creating them can be found using a wide search (breadth-first search, BFS). As mentioned below, it uses a queue to store intermediate results.

1. Queued state at creation.
2. We deduce a status from queue.
3. We receive the subsequent states, applying operations of transformation.
4. If there is no downward movement among them, the dequeued state is disabled.
5. We bring in the next state that we have not visited yet.
6. If the queue is not empty, repeat from step 2.

The program presents each state as an object with the following fields:

{ x, y, rotation, visited, predecessor }

During the preparation process, the program creates a three-dimensional array of state objects (20 rows × 10 columns × 4 turns), initializing x , y and rotation accordingly.

The visited field is marked when the status is enqueued. In BFS, this is permissible, because each subsequent state increases the total path length by 1. That is, by increasing the path length, it is impossible to create a subsequent state that needs to be inserted somewhere other than the end of the queue to maintain order.

The predecessor field points to the state object from which the current state originates. It is set when the status is queued. The state of creation has no preceding states.

The set of blocked states detected during the search is determined by the type of tetrimino and filled blocks on the playing field. The sequence of the moves that generated them can be clarified (in the reverse order) by following the predecessor links to the creation state. When the PLAY_FAST constant is PLAY_FAST to PLAY_FAST at the beginning of the program, it completely skips the preceding states by directly putting tetrimino on the field and blocking it.

A three-dimensional array of state objects, a queue, and a BFS are packed into a class. It has a search method that receives a playing field (two-dimensional array), a type of tetrimino and a listener. Each time a blocked state is detected, the playing field is updated by adding tetrimino to the appropriate place. Then, the modified playing field along with information about the changes is transmitted to the listener for processing. After the listener completes a return, the playing field is restored.

The listener is used to combine several search operations into a chain, which makes it possible to find all possible ways to add two (or more) tetrimino to the playing field. The first search engine in the chain performs BFS only once. However, the second search engine performs BFS every time the first search detects a blocked state. And so on, if there are other search engines in the chain.

The listener of the last search engine evaluates the changed playing field. When he finds the playing field better than what was previously investigated, he writes down the used object of the locked state, which at that time uses the first search engine in the chain. Since the first search engine performs BFS only once, the predecessor fields of its state objects remain valid until the entire search process is completed. That is, the last listener essentially writes down the path that the first tetrimino should take in order to come to the best configuration of the playing field as a result.

Evaluation function

The estimated function assigns a value to a modified game field — a weighted sum of the various influencing parameters. The evaluation function used in this case is based on the function developed by Islam Al-Ashi . It uses the following parameters:

• Total number of cleaned rows : this is the total number of rows that will be cleared due to the addition of two tetrimino.
• Total height of the block : the height of the block is the height above the floor of the playing field on which the figure is blocked. This is the vertical distance to which a blocked figure would fall, if you remove all other occupied squares of the playing field and preserve the orientation of the figure. The total blocking height is the sum of the blocking heights of two tetriminos.
• Total number of “well” cells : a cell-well is an empty cell located above all occupied cells in a column so that its left and right neighbors are occupied cells; in determining wells, the walls of the playing field are considered occupied cells. The idea is that the well is a structure that is open at the top, closed at the bottom and surrounded by walls on both sides. The likelihood of intermittent gaps in the walls of a well means that cell wells do not necessarily occur in a continuous heap within a column.
• The total number of holes in the columns : the hole in the column is an empty cell located directly below the occupied cell. The floor of the playing field is not compared with the cell above it. There are no holes in the empty columns.
• Total number of transitions in columns : a transition in columns is an empty cell adjacent to the occupied cell (or vice versa) within a single column. The combination of the topmost occupied column block with the empty space above it is not considered a transition. Similarly, the floor of the playing field is also not compared with the cell above it. Therefore, there is no transition in a completely empty column.
• Total number of transitions in the rows : the transition in the rows is an empty cell adjacent to the occupied cell (or vice versa) within one row. Empty slots near the walls of the playing field are considered transitions. The total number is calculated for all lines of the playing field. However, completely empty lines are not counted in the total number of transitions.

Al-Ashi suggested that useful weights can be found using the particle swarm optimization (PSO) algorithm, which iteratively improves the set of solutions by imitating the swarm behavior observed in nature. In our case, each solution is a vector of weights, and the fitness of a variant is determined by playing Tetris; this is the total amount of tetrimino during which he survived to the end of the game.

These ideas are applied in the Java version described below; it runs outside of FCEUX and can be configured for a non-graphical, memory-based game that runs at a much higher speed. After preparing the PSO, I was surprised to see that the algorithm does not move further after the initial iteration. After this iteration, several randomly generated solutions have already played quite well. For several days, the size of this set decreased until there was only one option left. Here are the values ​​for this solution:

Parameter	Weight
Total number of cleaned rows	1.000000000000000
Total lock height	12.885008263218383
Total number of well cells	15.842707182438396
The total number of holes in the columns	26.894496507795950
Total number of transitions in columns	27.616914062397015
Total number of transitions in lines	30.185110719279040

The playing field was estimated by multiplying the parameters by their respective weights and adding the results. The lower the value, the better the solution. Since all parameters and weights have positive values, all parameters harm the overall assessment; each must be minimized. It also means that the best score is 0.

Since these weights were chosen randomly, the range of suitable values ​​can be very wide. This particular set of numbers and the perceived relative importance of each parameter may not be significant. Nevertheless, it will be interesting to watch them carefully.

The least damaging parameter is the total number of rows cleared. The very fact that this parameter is harmful is counterintuitive. But the main goal of AI is survival. He does not aim for the most points. Instead, he plays conservatively, usually clearing the rows one by one. To get a Double, Triple or Tetris will have to grow a bunch, which goes against the long-term goal.

Next in the list is the total height of the lock. It can be minimized by dropping tetrimino as close to the floor as possible. This is a simple strategy that contributes to survival in the long run and, in the short run, to quality packaging of the pieces.

The weight assigned to the total number of well cells seems a little surprising, because experienced players usually deliberately build deep wells to collect several Tetris (combinations of four lines) in a row. But as mentioned above, this is a risky game, contrary to the main goal - survival. In addition, the number of wells is an indicator of "bumps" heap. A certain level of unevenness is beneficial when placing certain shapes or combinations of shapes. But high unevenness causes damage to the tight package.

The total number of holes in the columns is approximately half of the total number of transitions in the columns. These parameters can be combined and collapsed into a common related parameter, resulting in a more extensive and most harmful parameter: the total number of transitions.

The dense packing areas have a small number of transitions in all directions. Therefore, the basic strategy that drives artificial intelligence, can be briefly described as follows: pack the figures as close as possible to each other.

Other options

Here is a list of a few more parameters that I experimented with during the development of AI:

• Heap height : occupied blocks can hang over empty cells, creating protrusions and holes; however, it is impossible to fix occupied blocks above completely empty lines. Therefore, the height of the heap is the number of rows that contain at least one occupied block.
• Total number of columns occupied : this is the number of columns that contain at least one occupied cell.
• Total number of occupied cells : the number of occupied cells on the playing field.
• Total Number of Connected Areas : Here, the fill algorithm is used to count the number of continuously connected areas. In addition to finding busy "islands", he discovers holes that stretch along both axes.
• Variance of column heights : this is a statistical measure of the magnitude of the scatter of column heights. It is an indicator of surface roughness.
• Total Adaption Value : Calculates the heap adaptation value for the next unknown figure. It counts the total number of ways in which 7 types of pieces can be added to the playing field without the appearance of new holes. For accurate counting, multiple BFS applications will be required. But for an approximate count, the search tree can be very truncated.
• Average score of the next figure : this parameter deepens the search by analyzing all the possibilities for the next unknown figure. It uses other parameters for a separate arrangement of each type of figures, and then returns the average for 7 estimates. BFS is required for each shape placement.
• Averaged simulated game : the parameter simulates a series of games in Tetris, selecting figures using its own pseudo-random number generator and using AI to work with them. At the end of each game, the playing field is evaluated using other parameters. Returns the average for all batches.

All parameters can be customized by adding custom factors. For example, instead of simply counting the cleaned rows, you can assign your own weights for Single, Double, Triple and Tetris, by simulating a points system. If the simultaneous cleaning of several rows harms the long-term goal of survival, then a single weight can be assigned a negative weight, while others can get a positive one.

Another useful factor is the bias value. For example, a completely flat surface of a heap has a dispersion of the heights of columns 0. But a perfectly flat surface does not adapt to S and Z, as well as other combinations of figures. Therefore, by subtracting a constant, the variance needs to be centered around the optimal irregularity.

The adjusted and shifted parameters can be raised to any power so that they can be logarithmically or exponentially scaled before calculating the weighted sum. All these probabilities can be considered as additional weights that can potentially be optimized using methods like PSO.

Many of the parameters give an understanding of how well the heap can handle additional figures, for example, those dealing with surface roughness, but “Total Adaptation”, “Average score of the next figure” and “Average simulated game” estimate the modified playing field insertion of figures not included in the two known. In the study of subsequent figures due to the rapid elimination of rows, the amount of additional knowledge gained decreases with depth. This means that the past for a long time the party is not so important, and the course of the party in the distant future is also not very important. In fact, if the short sequence of pieces is randomly set incorrectly, the AI ​​quickly restores the course of the game, using the following few pieces to clear the affected rows. The determination of the optimal value of the analysis of subsequent figures requires further research.

Another aspect of parameter utility is computational overhead. Costs are greatly increased because the evaluation function is called for each possible placement of two figures. Since AI must be able to play Tetris in real time, costly factors providing valuable information can be exchanged for more approximate techniques that run faster.

AI training

There are pathological sequences that can lead to Game Over, regardless of strategy. The simplest example is an infinite sequence of T and S S and Z, which, as shown in the animation, quickly causes the AI ​​to lose.


Since it takes days to run the AI ​​variant until several batches are completed and the average is calculated, it is completely impractical to use the average batch duration as the PSO control metric. Instead, it is possible with controlled speed to increase the difficulty of the game, increasing the frequency of S and Z, which will eventually lead to the alternate creation of only this pair of figures.

I tried using this teaching method, but found that teaching AI to work with frequent S and Z actually harms the ability to cope with evenly distributed random figures.

In an alternative method, which I was inspired by the B-Type game, the PSO control metric is the frequency of cleaning rows. The game field is a scheme of 10 lines of random garbage blocks, and each time a line is cleaned, a new line of garbage appears at the bottom, restoring the height of the heap. Since the playing field is 10 columns wide, and each tetrimino consists of 4 squares, on average, the AI ​​should clear a row every 2.5 tetrimino. And to get rid of garbage, he must do it even faster.

Unfortunately, this technique also did not improve performance. One of the probable reasons is that random holes in the garbage do not exactly correspond to the lines that the AI ​​deals with in this gameplay. In addition, row cleaning is a short-term goal; greedy cleaning of the ranks will not necessarily improve long-term survival. From time to time, rows should not be touched to handle certain combinations of subsequent figures.

On his web page, Colin Fay suggested a different approach. He created a histogram showing the percentage of pieces blocked in each row during trial lots. Interestingly, all histograms look almost identical regardless of the number of created figures. Based on this, he suggested that it is possible to use an approximate image of a function for any trial game when evaluating the statistical waiting for a blockage in the creation line, thus obtaining the time during which the AI ​​will play until the end of the game. I decided to explore this opportunity.

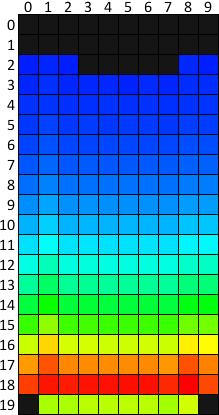
The following is a heat map of the set of test lots, in the amount containing 2,039,900,000 tetrimino. Each cell is colored based on the percentage of figures blocked in it. To enhance the visual contrast is selected non-linear palette. The map was created by normalizing the cell values ​​by dividing by the maximum percentage of cells, and then by announcing to a degree of 0.19 (see “gamma correction” ).

Colour Percent ■ 0.00000000 ■ 0.00000315 ■ 0.00024227 ■ 0.00307038 ■ 0.01860818 ■ 0.07527774 ■ 0.23582574 ■ 0.61928352 ■ 1.42923040 ■ 2.98867416 ■ 5.78182519

The dark orange and red bars in lines 17 and 18 mean that the vast majority of the figures end up there. The pale green tint below is a consequence of the geometry of the figures: only 4 of the 7 types of tetrimino can appear on the bottom line. The bottom corners are black because it’s impossible to be there.

The color along each line is almost uniform, and this suggests that horizontally the figures are distributed evenly. Minor gaps can be explained by looking at the histograms of certain types of shapes:

T

J

Z

O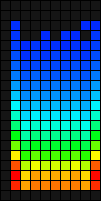

S

L

I

T turns out to be the most universal type: its histogram is more uniform than that of all others. Anomalies in the histogram J - the result of the influence of the walls; only Jr and Jl can be in the side columns, which causes the AI ​​to use columns 1 and 9 more often to compensate. The same applies to L. The histograms Z and S look about the same, which underlines the imbalance due to the fact that Zv and Sv not perfect mirror images of each other. Type O is limited to the 19 × 9 playing field, and it seems that the AI ​​tends to use O more often on the sides than in the center. Tetrimino I is shifted to the right, because its starting point is located there; therefore, blocking in column 1 rarely happens.

The table shows the percentage of figures blocked in each row.

Line	Percent
0	0.0000000000
one	0.0000000000
2	0.0000004902
3	0.0000026472
four	0.0000066180
five	0.0000172557
6	0.0000512280
7	0.0001759400
eight	0.0006681210
9	0.0023187901
ten	0.0077928820
eleven	0.0259672043
12	0.0866187068
13	0.2901315751
14	0.9771663807
15	3.3000408353
sixteen	10.6989059268
17	28.5687976371
18	50.0335706162
nineteen	6.0077671454

Here is a graph of values:


If you do not take into account line 19, the graph shows exponential growth.

.

A / B	(%)
1/2	0.00
2/3	18.52
3/4	40.00
4/5	38.35
5/6	33.68
6/7	29.12
7/8	26.33
8/9	28.81
9/10	29.76
10/11	30.01
11/12	29.98
12/13	29.85
13/14	29.69
14/15	29.61
15/16	30.84
16/17	37.45
17/18	57.10
18/19	832.81

16–19 , , . 0–5 , . , 6/7–14/15, ; 29.24%. , , . , Tetris .

log ₁₀ 6–15.


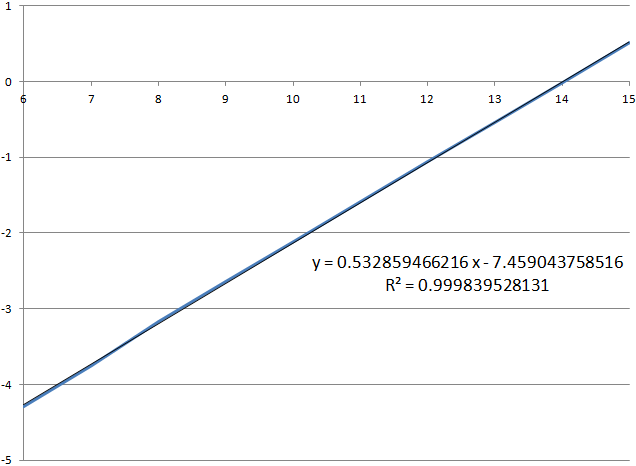
1 . , , Y, , 0 10 ^−7.459 %. , , 2 877 688 349 1 151 075 340 .

, log ₁₀ 0. , , . , 0 game over; , .

. 5 . , , O. , 4 , — 10 , 5 ( 4×5n = 2×10n ).

1181 — . , , game over. SZ , .

( ) , .


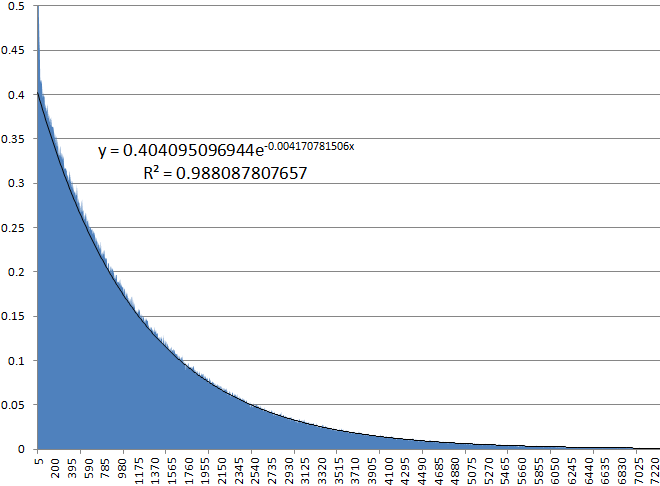
, , . , 0,4% 1 253 , , 5 .

, , , R ² 1, PSO. , , , . PSO, , , .

Java

About the program

, Lua, zip- Java. Lua .

Packages

:

• tetris.ai .
• tetris.gui .

Tetriminos . enum :

 public static final int NONE = -1; public static final int T = 0; public static final int J = 1; public static final int Z = 2; public static final int O = 3; public static final int S = 4; public static final int L = 5; public static final int I = 6; 

NONE . .

Tetriminos . PATTERNS — 4- integer ( × × × ), ; , . ORIENTATIONS — , 2- ( × ) Orientation . Orientation Point . , .

 public class Orientation { public Point[] squares = new Point[4]; public int minX; public int maxX; public int maxY; ... } 

 public class Point { public int x; public int y; ... } 

( ) State , BFS.

 public class State { public int x; public int y; public int rotation; public int visited; public State predecessor; public State next; ... } 

x , y rotation . , .

Searcher , BFS, State :

 private void createStates() { states = new State[AI.PLAYFIELD_HEIGHT][AI.PLAYFIELD_WIDTH][4]; for(int y = 0; y < AI.PLAYFIELD_HEIGHT; y++) { for(int x = 0; x < AI.PLAYFIELD_WIDTH; x++) { for(int rotation = 0; rotation < 4; rotation++) { states[y][x][rotation] = new State(x, y, rotation); } } } } 

Java Collections API, Searcher . Queue State.next State . State , State , , -, .

«» BFS search .

 public boolean search(int[][] playfield, int tetriminoType, int id) { int maxRotation = Tetriminos.ORIENTATIONS[tetriminoType].length - 1; int mark = globalMark++; if (!addChild(playfield, tetriminoType, mark, null, 5, 0, 0)) { return false; } while(queue.isNotEmpty()) { State state = queue.dequeue(); if (maxRotation != 0) { addChild(playfield, tetriminoType, mark, state, state.x, state.y, state.rotation == 0 ? maxRotation : state.rotation - 1); if (maxRotation != 1) { addChild(playfield, tetriminoType, mark, state, state.x, state.y, state.rotation == maxRotation ? 0 : state.rotation + 1); } } addChild(playfield, tetriminoType, mark, state, state.x - 1, state.y, state.rotation); addChild(playfield, tetriminoType, mark, state, state.x + 1, state.y, state.rotation); if (!addChild(playfield, tetriminoType, mark, state, state.x, state.y + 1, state.rotation)) { lockTetrimino(playfield, tetriminoType, id, state); } } return true; } 

, , , .

search , , . BFS .

 public interface ISearchListener { public void handleResult(int[][] playfield, int tetriminoType, int id, State state); } 

, . . State , . State.predecessor , State .

State.visited boolean ; State visited false . visited int , , .

addChild . 4 . , State . , addChild true , , .

search addChild , . , ; false .

addChild . , lockTetrimino . lockTetrimino , , .

playfield 1 , . lockTetrimino , .

, PlayfieldUtil.clearRows ; , . , Java ; . PlayfieldUtil ; , . . .

PlayfieldUtil.restoreRows , . . . . . , , — .

PlayfieldUtil evaluatePlayfield , 4 -.

 public class PlayfieldEvaluation { public int holes; public int columnTransitions; public int rowTransitions; public int wells; } 

AI . Searcher , .

 public void handleResult( int[][] playfield, int tetriminoType, int id, State state) { if (id == 0) { result0 = state; } Orientation orientation = Tetriminos.ORIENTATIONS[tetriminoType][state.rotation]; int rows = playfieldUtil.clearRows(playfield, state.y); int originalTotalRows = totalRows; int originalTotalDropHeight = totalDropHeight; totalRows += rows; totalDropHeight += orientation.maxY - state.y; int nextID = id + 1; if (nextID == tetriminoIndices.length) { playfieldUtil.evaluatePlayfield(playfield, e); double fitness = computeFitness(); if (fitness < bestFitness) { bestFitness = fitness; bestResult = result0; } } else { searchers[nextID].search(playfield, tetriminoIndices[nextID], nextID); } totalDropHeight = originalTotalDropHeight; totalRows = originalTotalRows; playfieldUtil.restoreRows(playfield, rows); } 

AI Searcher , Nintendo Tetris . Searcher , . , Searcher.search , , . Searcher . , . , State Searcher .

AI search , , . State , , . ; . Searcher , AI.search null .

 public State search(int[][] playfield, int[] tetriminoIndices) { this.tetriminoIndices = tetriminoIndices; bestResult = null; bestFitness = Double.MAX_VALUE; searchers[0].search(playfield, tetriminoIndices[0], 0); return bestResult; } 

Java FCEUX, . , - , .

-, AI , PlayfieldUtil . , PlayfieldUtil.createPlayfield ; , . , .

 AI ai = new AI(); PlayfieldUtil playfieldUtil = new PlayfieldUtil(); int[] tetriminos = new int[AI.TETRIMINOS_SEARCHED]; int[][] playfield = playfieldUtil.createPlayfield(); Random random = new Random(); 

, Tetriminos.NONE . , playfield[rowIndex][AI.PLAYFIELD_WIDTH] .

, .

 tetriminos[0] = random.nextInt(7); tetriminos[1] = random.nextInt(7); 

AI.search . State , . null , game over.

 State state = ai.search(playfield, tetriminos); 

, State AI.buildStateList .

 State[] states = ai.buildStatesList(state); 

PlayfieldUtil.lockTetrimino State . .

 playfieldUtil.lockTetrimino(playfield, tetriminos[0], state); 

AI.search .

 tetriminos[0] = tetriminos[1]; tetriminos[1] = random.nextInt(7); 

:

 AI ai = new AI(); PlayfieldUtil playfieldUtil = new PlayfieldUtil(); int[] tetriminos = new int[AI.TETRIMINOS_SEARCHED]; int[][] playfield = playfieldUtil.createPlayfield(); Random random = new Random(); tetriminos[0] = random.nextInt(7); tetriminos[1] = random.nextInt(7); while(true) { // ... print playfield ... State state = ai.search(playfield, tetriminos); if (state == null) { break; // game over } playfieldUtil.lockTetrimino(playfield, tetriminos[0], state); tetriminos[0] = tetriminos[1]; tetriminos[1] = random.nextInt(7); } 

…

TetrisFrame Nintendo Tetris, , .


, tetris.gui.Main . Lua, .

 public static final boolean PLAY_FAST = true; 

TetrisFrame 4 . displayTetrimino . , .

 public void displayTetrimino(int type, int rotation, int x, int y, int delay) 

lockTetrimino . , , , . animate true Tetris. .

 public void lockTetrimino(int type, int rotation, int x, int y, boolean animate) 

updateStatisticsAndNext .

 public void updateStatisticsAndNext(int activeTetrimino, int nextTetrimino) 

dropTetrimino «», . Main , AI.search null . animate true , . , . true , .

 public boolean dropTetrimino(int type, boolean animate) 

4 , TetrisFrame Event Dispatch Thread. , , . Main .

Main Randomizer , Nintendo Tetris.

tetris.gui.images . tiles.png — , . background.dat , ; $BF3F . colors.dat , , 138.

ImageLoader NES, ImagePane .

Other projects

. , , . , seed , . . , . ( 49 ), seed , . , , . , , .

« ». «» , . , B-Type. , , , . , . , IChildFilter .

 public interface IChildFilter { public boolean validate(int[][] playfield, int tetriminoType, int x, int y, int rotation); } 

AI , IChildFilter . IChildFilter.validate ; false , .

WellFilter — IChildFilter , (Tetris). , , . , , . - , . 4 , «» Tetris. , ; , WellFilter .


, Main :

 AI ai = new AI(new WellFilter()); 

WellFilter , . , . Tetris , , , PSO.

, . , PatternFilter .


PatternFilter , , WellFilter ; PatternFilter , .

PatternFilter tetris.gui.patterns , . 20×10 , .

 AI ai = new AI(new PatternFilter("tetriminos")); 

.


T, .


One more example. , .


WellFilter , PatternFilter , proof of concept. - , game over. , , .

Lua Java ; , , . - Tetris, . zip- Lua, , , .

, . , . Here are the most important ones:

• : , .
• «» .
• «» «» .
• .
• .
• .
• .
• , .
• A B .
• «» «» 6 16 . «» «» , .
• «» 3 .
• 96 . , — .

, . , . , x , y . , , . .

State :

 { x, y, rotation, Left, Right, Down, A, B, fallTimer, visited, predecessor } 

. , , , . , A B. Left , Right , A B , :

 { RELEASED, PRESSED } 

, «», 4 :

 { RELEASED, PRESSED_FOR_1_FRAME, PRESSED_FOR_2_FRAMES, PRESSED_FOR_3_FRAMES } 

Down RELEASED PRESSED_FOR_3_FRAMES , . RELEASED PRESSED_FOR_2_FRAMES , . RELEASED PRESSED_FOR_1_FRAME PRESSED_FOR_2_FRAMES .

Lua , .

visited predecessor , fallTimer , ; fallTimer . , fallTimer , , , , fallTimer 0.

Searcher 8- , ( 20 × 10 × 4 × 2 × 2 × 4 × 2 A × 2 B ), BFS , . , .

 Slide = (Left == PRESSED) or (Right == PRESSED) Rotate = (A == PRESSED) or (B == PRESSED) if Down == RELEASED or Down == PRESSED_FOR_3_FRAMES then if Down == RELEASED then nextDown = PRESSED_FOR_1_FRAME else nextDown = PRESSED_FOR_2_FRAMES end addChild(Down = nextDown) if not Rotate then addChild(A = PRESSED, Down = nextDown) addChild(B = PRESSED, Down = nextDown) end if Slide then addChild() if not Rotate then addChild(A = PRESSED) addChild(B = PRESSED) end else addChild(Left = PRESSED) addChild(Right = PRESSED) if not Rotate then addChild(Left = PRESSED, A = PRESSED) addChild(Left = PRESSED, B = PRESSED) addChild(Right = PRESSED, A = PRESSED) addChild(Right = PRESSED, B = PRESSED) end end else if Down == PRESSED_FOR_1_FRAME then nextDown = PRESSED_FOR_2_FRAMES else nextDown = PRESSED_FOR_3_FRAMES end addChild(Down = nextDown) if not Rotate then addChild(A = PRESSED, Down = nextDown) addChild(B = PRESSED, Down = nextDown) end end 

, addChild , (, , ).

 nextFallTimer = fallTimer + 1 if Left == PRESSED and testPosition(x - 1, y, rotation) then x = x - 1 elseif Right == PRESSED and testPosition(x + 1, y, rotation) then x = x + 1 end if A == PRESSED and testPosition(x, y, nextClockwiseRotation) then rotation = nextClockwiseRotation elseif B == PRESSED and testPosition(x, y, nextCounterclockwiseRotation) then rotation = nextCounterclockwiseRotation end if Down == PRESSED_FOR_3_FRAMES or nextFallTimer >= dropSpeed then if testPosition(x, y + 1, rotation) then y = y + 1 nextFallTimer = 0 else lockTetrimino() return end end childState = states[y][x][rotation][Left][Right][Down][A][B] if not childState.visited then childState.visited = mark childState.predecessor = state childState.fallTimer = nextFallTimer queue.enqueue(childState) end 

, AI.search State . State , . x , y rotation , .

, 1–3 . , . , ; . , , , .

, lua/NintendoTetrisAIGamepadVersion.lua , zip- .

, , . , , ; , — , . , , , . , . , «», , .

Addition

, «». :

1. , , Nintendo Tetris. , . , . , .
2. . — , . Double, Triple Tetris, — , . 90. , , 29 - .
3. . . . , Tetris .

, Nintendo Tetris . , .

---

Video

, Nintendo Tetris, 19 .

---

TetrisAI_2018-01-28.zip

.zip :

• src — .
• TetrisAI.jar — .
• lgpl-2.1.txt — .

---

Prerequisites

• Nintaco — NES / Famicom.
• Tetris (U) [!].nes — ROM- Nintendo Tetris.

1. Nintaco Tetris (U) [!].nes .
2. TetrisAI.jar .zip .
3. Run Program, Tools | Run Program...
4. JAR Find JAR… .
5. Load JAR, .
6. Run.
7. , GAME TYPE MUSIC TYPE . D-pad ( ) A-TYPE . Start (Enter), .
8. A-TYPE D-pad ( ) LEVEL 9 . , A Start ( X Enter), 19, .

, 19 . .

, Machine | Speed | Max.

---

Details

10 , . 10 , . . , . : 10–12, 13–15, 16–18, 19–28 29+ 5, 4, 3, 2 1 .

19–28. «», «», A, B . , . , , ; .

, , (Delayed Auto Shift, DAS), «», . . , .

40, 100, 300 1200 Single, Double, Triple Tetris. 1. , Tetris, .

19 , , 19–28. , , 20 140 , 200. 10 . 230 . Tetris 230 .

. . , , . . , .

. , , «» . .

. — , , . , . BSF.

: 4 , , . , . SearchChain .

, . . . , .

— :

• – , .
• – , . — , , .
• - – .
• – , -.
• – , . . .
• – . , 1. , , .
• – , . — , — .
• – . , (20).
• – . , 0.
• – , ( ) .
• : — , ( ) . . . .
• – . , 1 , 1, — 0.
• – .
• – .
• – .
• – . .
• – .

Machine learning

(Particle Swarm Optimization, PSO), [1]. . .

, . , ( ), PSO , .

100 19–28. 230 , . , 33 100 . . , . , «».

100 PSO, . , , . PRNG Nintendo Tetris, . PRNG (. « » ): .

, . 19–28, . , , . «» :

1. : Tetris, . «» . . ; 230 . , Tetris . Single, Double Triple. ; .
2. . , , 7 . .
3. , , . , 7 .
4. , , . , . , .

«» , PSO :

Parameter	Weight
	0.286127095297893900
	1.701233676909959200
-	0.711304230768307700
	0.910665415998680400
	1.879338064244357000
	2.168463848297177000
	−0.265587111961757270
	0.289886584949610500
	0.362361055261181730
	−0.028668795795469625
	0.874179981113233100
	−0.507409683144361900
	−2.148676202831281000
	−1.187558540281141700
	−2.645656132241128000
	0.242043416268706620
	0.287838126164431440

, , , , , — . ; , .

1,7 ( ) 19–28. 29 , , . , - . PRNG Nintendo Tetris.

1 313 600. — 0.

816 379, , . , , — 989 200 .

, PSO . 1 108 860. 75% 1 000 000.

47% 29. 61% 900 000 29. 29.


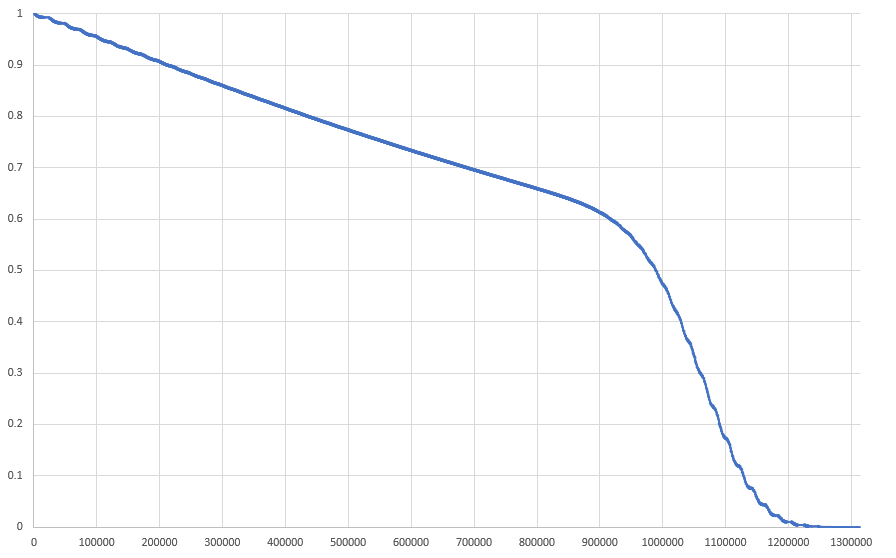
, 900 000 . .

. .


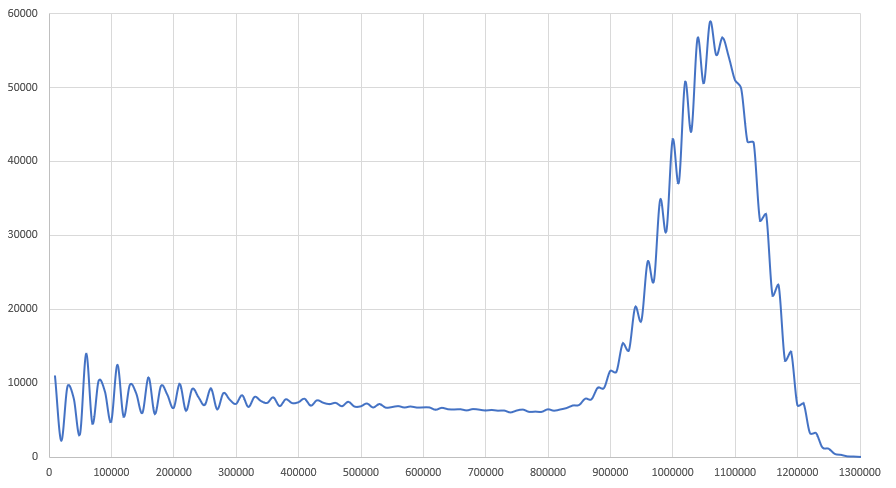
, 900 000 , 1 050 000 . . , , 20 000 . , Tetris.

, Nintaco API . Nintaco, Data Crystal ROMhacking.net wiki . Addresses .

---

1. van den Bergh, F.; Engelbrecht, AP (2006)
   A study of particle swarm optimization particle trajectories
   In: Information Sciences 176 (2006) (pp. 937–971)
   Retrieved from http://researchspace.csir.co.za/dspace/bitstream/handle/10204/1155/van%20den%20bergh_2006_D.pdf