We select the password to the Indian TIN for two seconds, or why brute force math

In India, there is a local analogue of our TIN - “adhar”. The electronic system "eAdkhar" is fastened to it. In eHadhara, every letter is blocked with a password. And everything would be fine, but the password is composed according to a simple pattern: the first four letters of the name caps plus the year of birth.

Four capital letters and four numbers. Of these, you can make 2,821,109,907,4456 combinations. If you check a thousand combinations per second, one password will take ninety years.

Long Can accelerate a couple ( billion ) times?

92 years → 52 days. Grouping

With three trillion combinations, we barely had enough. Still, the pattern is known:

([AZ][AZ][AZ][AZ]) ([0–9][0–9][0–9][0–9]) (4  ) (4 ) ( 1) ( 2) 

Considering this pattern, lines like S2N65GE1 can be immediately discarded. How many combinations will you get then?

The first group is four letter symbols. 26 options, 4 positions, we get:

$$

$$26 ^ 4 = 456,976$$

4 positions of 10 digits, similarly:

$$

$$10 ^ 4 = $ 10,00$$

From this we get the total number of combinations:

$$

$$456976 × 10000 = 4569760000$$

Let us estimate how much faster brutfors will be now. Again we proceed from 1000 attempts per second:

$$

$$4569760000/1000 = $ 456976$$

Or 52 days, 21 hours, 22 minutes and 40 seconds. Instead of 92 years. Not bad. But still long. What else can you do? The same is to reduce the number of combinations.

52 days → 12 hours. Turn on common sense

The first and second group is not a random set of characters, but the first letters of the name and year of birth. Let's start with the year of birth.

There is no sense in selecting passwords for those born in 1642 or 2594. So the range of combinations can be safely reduced from 0000–9999 to 1918–2018. So we will cover the plus or minus of all those living between 0 and 100 years old. This reduces the number of combinations and time, respectively:

$$

$$456976 × 100 = 45 697 600$$

$$

$$45697600/1000 = 45697.6$$

Or 12 hours, 41 minutes and 37 seconds.

12 hours → 2 minutes. Sacrifice accuracy

12 hours is cool, but ... We need to go deeper .

We now have 45 million combinations that accurately cover all eAdhara users. But what if you donate them a small fraction for the sake of speed increase?

Digital combinations, we have perfected. Letters do something similar. The logic is simple: there is no year of birth 9999, and in the same way there is no Indian name c "AAAA" in the beginning. But how to determine all suitable combinations?

I collected Indian names from the catalog site, Photon helped me a lot with this. The result was 3,283 unique names. It remains to trim the first four letters and remove duplicates:

 grep -oP ”^\w{4}” custom.txt | sort | uniq | dd conv=ucase 

It turned out 1 598 prefixes! There were quite a few duplicates, because the first four letters in such names as “Sanjeev” and “Sanjit” are the same.

1 598 prefixes - not enough for the one and a half billion population? I agree. But do not forget that these are prefixes, not names. I posted the resulting list on Gist . In fact, there should be more. You can be confused, collect 10,000 names from other sites and get 3,000 unique prefixes, but I didn’t have time for that. So we will make a start from 1 598.

Calculate how much time you need now:

$$

$$1598 × 100 = $ 15980$$

$$

$$159800/1000 = $ 159.$$

Or 2 minutes and 39.8 seconds.

2 minutes → 2 seconds. Wikipedia help

2 minutes 40 seconds is the time it takes to go through all the combinations. And what if the eleventh combination is correct? Or the last? Or the first?

Now the list of combinations sorted alphabetically. But it is meaningless - who said that the names in “A” are more common than in “B”, or that there are more than one year old children than seventy-year olds?

It is necessary to take into account the probability of each combination. On Wikipedia write:

In India, more than 50% of the population is under 25 and more than 65% is under 35.

Based on this, instead of a list of 1–100, you can try this:

 25–01 (  ,       ,     ) 25–35 36–100 

Then it turns out that the probability of the first $$$1598 × 25 = $ 39,95$ combinations increases to 50%. We cracked half the passwords for $$$39950/1000 = $ 39.9$ seconds! In the following $$$1598 × 10/1000 = $ 15.$ seconds, we will pick up another 15% of passwords. Total - 65% of passwords in 55.9 seconds.

Now to the names.

In Google it is easy to find the TOP-100 names of any country. Based on data from India, I moved the appropriate combinations to the top of the list. We assume that 15% of the population of India has popular names. So 15% of passwords can be cracked almost instantly.

Hindu - 80% of the population of India. So, if you put the Hindu names higher in the list, it will speed up 80% of attempts. After the previous step we have left $$$100% - 15% = 85%$ attempts. If 80% of them are Hindu names, then 79% (leaving 1% for popular, but not Hindu names) we will hack into the next 65% of attempts.

We calculate everything together, taking into account age statistics. We divide into groups:

 100:   { 50:  00  25  { 7:  , 43:   { 34: , 9:   } } 15:  26  35  { 3:  , 13*:   { 10: , 3:   } } 45:  36  100  { 7:  , 38:   { 30: , 8:   } } } 

Now we will make an effective password cracking algorithm:

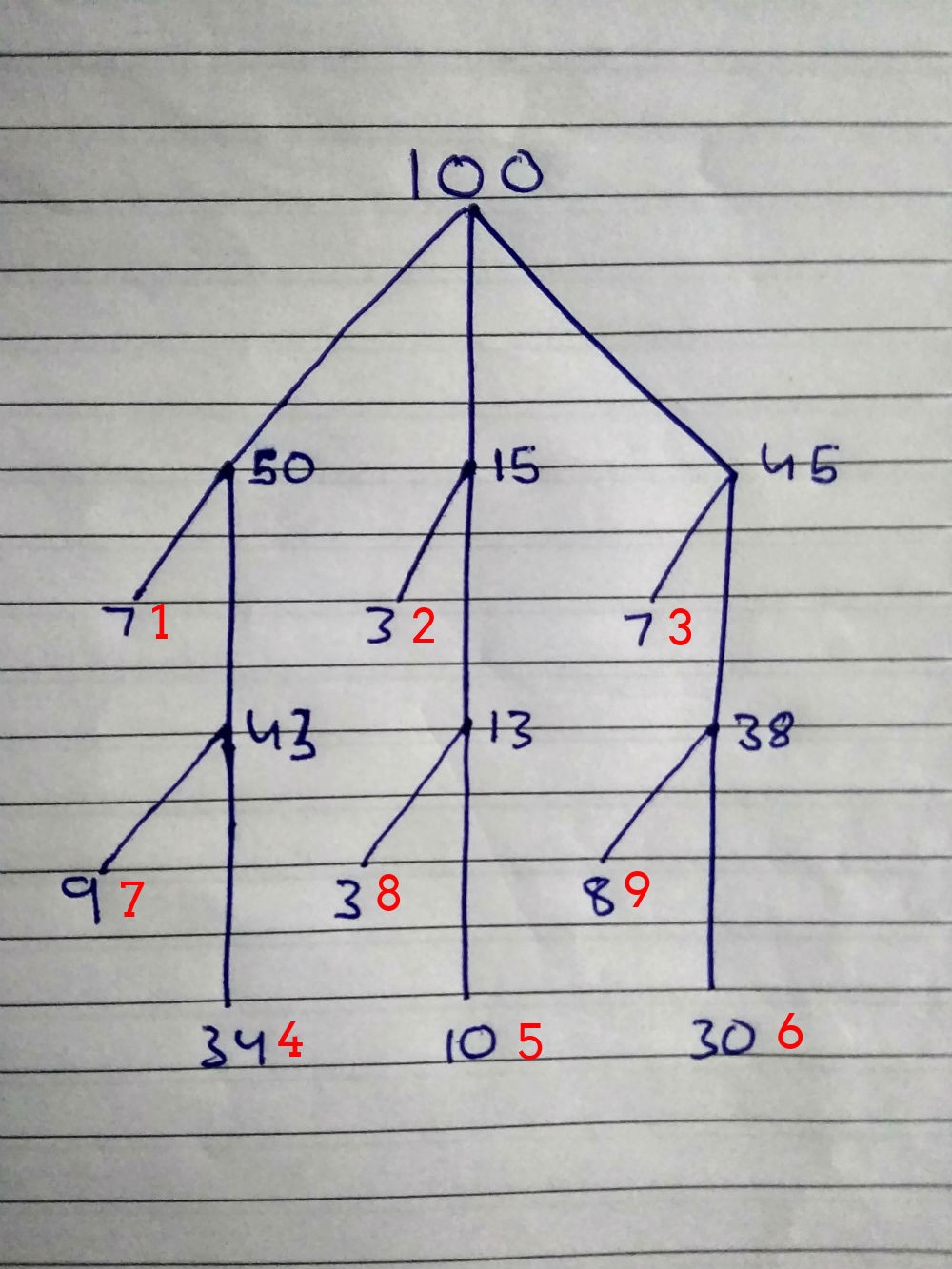
Red numbers are a search priority. We will test the combinations for the people of the first group first, then the second, then the third, and so on.

How much time is needed now for hacking?

Phase number 1
1 = 11 seconds to crack 7 passwords
2 = 3 seconds to crack 3 passwords
3 = 11 seconds to crack 7 passwords

We cracked the passwords of 17 people, 83 left. Delete the previous combinations from the list and we will try the following sets - 4, 5, 6.

Phase 2
4 = 54 seconds to crack 34 passwords
5 = 16 seconds to crack 10 passwords
6 = 47 seconds to crack 30 passwords

Again, remove the combination of the previous phases.

Phase 3
7 = 14 seconds to crack 9 passwords
8 = 5 seconds to crack 3 passwords
9 = 12 seconds to crack 8 passwords

Total time : $$$11 + 3 + 11 + 54 + 16 + 47 + 14 + 5 + 12 = $ 17$ seconds or 2 minutes and 13 seconds.

Hacked passwords : 100

Average time for one password : $$$173/100 = 1.73$ seconds

92 years → 1.73 seconds. So, yes?