The principle of least action. Part 1

When I first learned about this principle, I had a feeling of some kind of mysticism. It seems that nature mysteriously sorts through all possible paths of movement of the system and selects the best of them.

Today I want to talk a little bit about one of the most remarkable physical principles - the principle of least action.

Prehistory

Since the time of Galileo, it has been known that bodies, on which no forces act, move along straight lines, that is, along the shortest path. Light lines propagate along straight lines.
')
When reflected, the light also moves in such a way as to get from one point to another in the shortest way. In the picture, the shortest path will be the green path at which the angle of incidence equals the angle of reflection. Any other path, such as red, will be longer.


It is easy to prove, simply reflecting the path of the rays on the opposite side of the mirror. In the picture they are shown dotted.


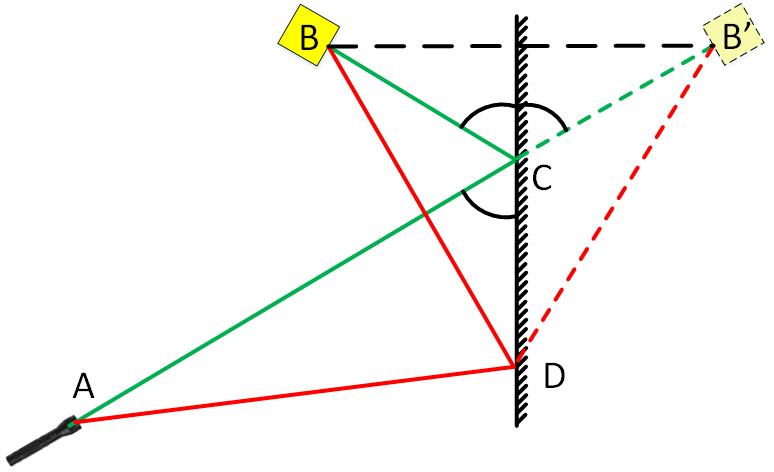
It can be seen that the green ACB path turns into a direct ACB '. And the red path turns into a broken ADB 'line, which, of course, is longer than the green one.

In 1662, Pierre Fermat suggested that the speed of light in a dense substance, for example, in glass, is less than in air. Prior to this, there was the generally accepted version of Descartes, according to which the speed of light in a substance must be greater than in air in order to obtain the correct law of refraction. For Fermat, the assumption that light can move in a denser environment faster than in a rarefied seemed unnatural. Therefore, he suggested that everything was exactly the opposite and proved an amazing thing - with such an assumption, the light is refracted so as to reach the destination in the shortest possible time.


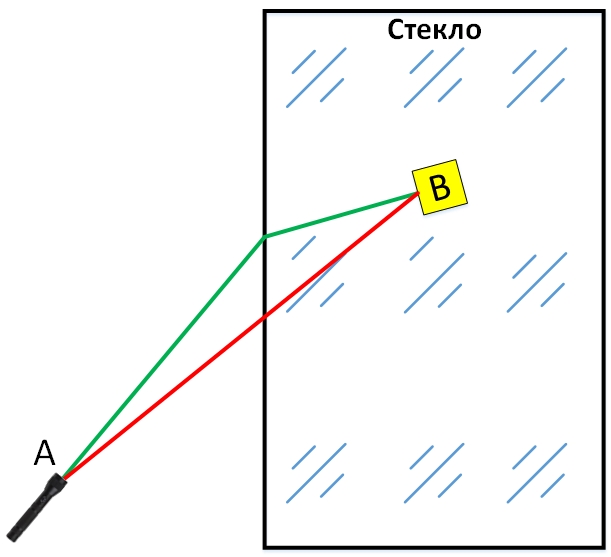
The figure again shows in green the path that the light beam actually moves. The path marked in red is the shortest, but not the fastest, because the light has to travel a greater way in the glass, and in it its speed is less. The fastest is the real path of the light beam.

All these facts suggested that nature acts in some rational way, the light and bodies move in the most optimal way, expending as little effort as possible. But what kind of effort, and how to count them remained a mystery.

In 1744, Maupertuis introduced the concept of "action" and formulated the principle that the true trajectory of a particle differs from any other in that the action for it is minimal. However, Maupertuis himself could not give a clear definition of what this action is equal to. The rigorous mathematical formulation of the principle of least action was already developed by other mathematicians - Euler, Lagrange, and was finally given by William Hamilton:


In mathematical language, the principle of least action is formulated rather briefly, but the meaning of the notation used may not be clear to all readers. I want to try to explain this principle more clearly and in simple words.

Free body

So imagine that you are sitting in the car at $$ and at the time $$ you are given a simple task: by the time $$ you need to drive to the point $$ .


Fuel for the car is expensive and, of course, you want to spend it as little as possible. Your car is made with the latest super-technologies and can accelerate or brake as you please quickly. However, it is arranged in such a way that the faster it goes, the more it consumes fuel. Moreover, fuel consumption is proportional to the square of the speed. If you drive twice as fast, then during the same period of time you consume 4 times more fuel. In addition to speed, the weight of the car also affects fuel consumption. The heavier our car, the more fuel it consumes. Our car's fuel consumption at any one time is equal to $$ i.e. exactly equal to the kinetic energy of the car.

So how do you need to go to get to the point $$ at exactly the right time and use less fuel? It is clear that you need to go in a straight line. As the driving distance increases, the fuel is consumed exactly no less. And then you can choose different tactics. For example, you can quickly arrive at the point $$ just sit and wait before the time comes $$ . The driving speed, and hence the fuel consumption at each time point, will turn out to be high, but then the driving time will be reduced. Perhaps the total fuel consumption will not be that great. Or you can drive evenly, at the same speed, so that, without haste, just come at a time $$ . Or part of the road to drive fast, and some slower. How better to go?

It turns out that the most optimal, most economical way to drive is to drive at a constant speed, such as to get to the point $$ at exactly the appointed time $$ . Under any other variant, more fuel will be consumed. You can check for yourself with a few examples. The reason is that fuel consumption increases in proportion to the square of the speed. Therefore, with an increase in speed, fuel consumption increases faster than driving time decreases, and overall fuel consumption also increases.

So, we found out that if a car consumes fuel at any one time in proportion to its kinetic energy, then the most economical way to get from a point $$ exactly $$ by the precisely designated time it is to travel evenly and straightforwardly, just as the body moves in the absence of forces acting on it. Any other method of driving will lead to greater overall fuel consumption.

In the field of gravity

Now let's improve our car a little. Let's attach jet engines to it so that it can fly freely in any direction. In general, the design remained the same, so the fuel consumption again remained strictly proportional to the kinetic energy of the car. If the task is now given to fly out of a point $$ at the moment of time $$ and fly to the point $$ to the point in time $$ then the most economical way, as before, of course, will fly evenly and straightforwardly to be at the point $$ at exactly the appointed time $$ . This again corresponds to the free movement of the body in three-dimensional space.


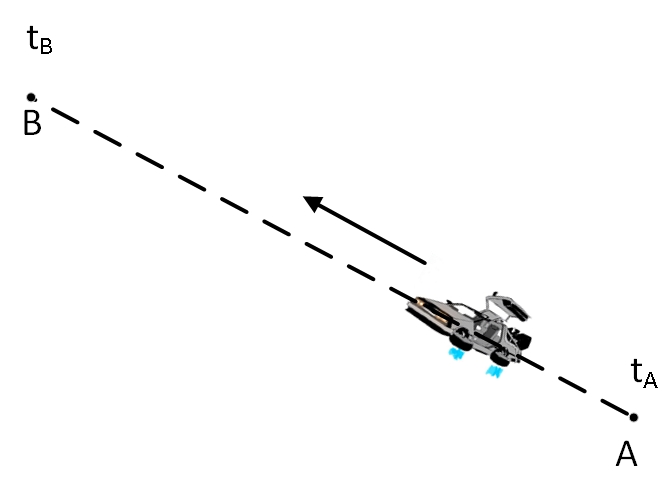
However, in the latest car model installed an unusual machine. This unit can produce fuel from virtually nothing. But the design is such that the higher the car is, the more fuel the vehicle produces at each time point. Fuel production is directly proportional to height $$ on which the car is currently located. Also, the heavier the car, the more powerful the device is installed on it and the more fuel it produces, and the output is directly proportional to the mass of the car. $$ . The device turned out such that the production of fuel is exactly equal to $$ (Where $$ - gravitational acceleration), i.e. the potential energy of the car.

The fuel consumption at each time point is equal to the kinetic energy minus the potential energy of the car (minus the potential energy, because the installed machine produces fuel, and does not waste it). Now our task is the most economical movement of the vehicle between points. $$ and $$ getting harder. Rectilinear uniform motion is not the most effective in this case. It turns out that it is more optimal to gain a bit of height, stay there for a while, develop more fuel, and then go down to a point. $$ . With the right flight path, total fuel generation due to climb will override additional fuel costs to increase the path length and increase speed. If you carefully calculate, then the most economical way for a car would be to fly along a parabola, exactly along such a trajectory and with exactly the speed with which a stone would fly in the field of gravity of the Earth.


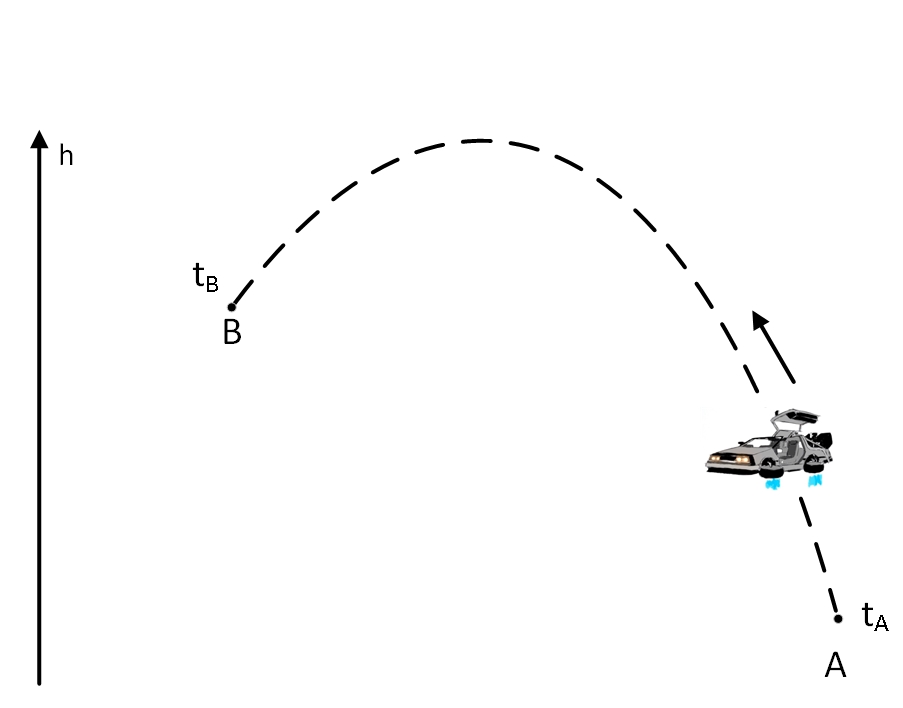
Here it is worth making an explanation. Of course, you can from a point $$ throw a stone in many different ways so that it hits the mark $$ . But you need to throw him so that he, taking off from the point $$ at the moment of time $$ got to the point $$ exactly at the moment of time $$ . This movement will be the most economical for our car.

Lagrange function and the principle of least action

Now we can transfer this analogy to real physical bodies. An analogue of the intensity of fuel consumption for bodies is called the Lagrange function or Lagrangian (in honor of Lagrange) and is denoted by the letter $$ . Lagrangian shows how much "fuel" the body consumes at a given time. For a body moving in a potential field, Lagrangian is equal to its kinetic energy minus potential energy.

The analogue of the total amount of fuel consumed during the whole period of movement, i.e. the value of Lagrangian accumulated over the entire time of movement is called “action”.

The principle of least action is that the body moves in such a way that the action (which depends on the trajectory of movement) is minimal. It should not be forgotten that the initial and final conditions are specified, i.e. where the body is at time $$ and at the time $$ .

In this case, the body does not necessarily have to move in a uniform field of aggression, which we considered for our car. You can consider completely different situations. The body can oscillate with a rubber band, swing on a pendulum or fly around the sun, in all these cases it moves so as to minimize “total fuel consumption” i.e. act.

If the system consists of several bodies, then Lagrangian of such a system will be equal to the total kinetic energy of all bodies minus the total potential energy of all bodies. And again, all bodies will move in a coordinated manner so that the action of the entire system during such a movement is minimal.

Not so simple

In fact, I was a little deceived, saying that the bodies always move so as to minimize the action. Although in many cases this is true, you can come up with situations in which the action is clearly not minimal.

For example, take the ball and place it in the empty space. At some distance from him put an elastic wall. Suppose we want the ball to be in the same place after some time. Under such specified conditions, the ball can move in two different ways. First, he can just stay in place. Secondly, you can push it towards the wall. The ball will fly to the wall, bounce off of it and come back. It is clear that you can push it so fast that it returns at exactly the right time.


Both variants of the ball movement are possible, but the action in the second case will be more, because all this time the ball will move with non-zero kinetic energy.

How to save the principle of least action, so that it is fair in such situations? We will talk about this next time .